基于单纯形优化算法的火箭弹增程研究

张 斌，陈国光，王 捷

（1.中北大学，山西太原 030051；2.西南技术物理研究所，四川成都 610041）

为满足当前远距离、精确化、大威力的现代战争作战要求，火箭弹增程技术当前已成为当前研究的热点之一。目前，火箭弹增程方法有提高发动机总冲、改良火箭弹结构以及增添舵机控制的滑翔增程等。单就结构和推进剂的改良而言，增程效果并不佳。依据弹道修正弹弹道特性分析，采用舵机控制的滑翔增程方法不仅能有效增加射程，还能减少因火箭弹增大射程而带来的散布问题。

滑翔增程是通过调整舵翼偏转来控制火箭弹的升力，使火箭弹缓慢下降，进而延长飞行时间，达到增程的目的。这种增程方法是基于弹箭飞行特性提出的，对制导控制及弹道修正有着重要指导意义。经查阅文献了解，目前增程方案有：分析增程原理和弹道特点，控制重力法向方向始终平衡的方案；采用控制火箭弹法向过载最优的方案；采用数值解算最大升阻比的思想建立滑翔段模型；以能量法研究滑翔弹道，最小能量损失的弹道设计；对滑翔段进行分段控制，保证舵偏角在每1小段都不变，探究分段次数与增程的关系；依据气动力参数，拟合最大升阻比下的攻角随马赫数的变化曲线及攻角随时间的函数，实现滑翔增程；以射程为优化变量，采用序列二次规划优化算法，进行数值仿真；采用现代优化算法，对弹道进行全局约束搜索最优攻角方案。

目前，多采用地面雷达监测及发射指令的方式修正弹道，对于高速短时作战的弹药而言，这种方法存在时间误差和预测偏差等问题，修正效果并不理想。

基于此，本文从能量法角度分析并提出了1种基于弹载计算机实时优化的改进单纯形优化算法，在SIMULINK 中建立弹道模型，并将优化算法模块化，嵌套在仿真程序中，跟随弹道解算过程对攻角进行实时优化。通过该算法，能快速找到当前弹道诸元（速度、高度、弹道倾角等）下的最优控制量。通过仿真分析验证了算法有效性。

1 模型建立

本文的研究对象是某型制导火箭弹，其采用双通道舵机，卷弧尾翼。三维弹体模型，如图1所示。

图1 制导火箭弹模型Fig.1 Guided rocket model

对于双通道控制舵机，升降舵和方向舵是分开控制的：升降舵主要控制火箭弹在纵向平面的射程修正；方向舵则控制水平面的偏差量修正。本文主要研究火箭弹在纵向平面的增程问题。

1.1 滑翔增程弹原理

制导火箭弹通常在弹道前期无控飞行，飞行到弹道顶点附近打开舵机，通过电机驱动舵翼偏转，调整弹体的升力，减小或平衡弹丸在速度矢量法向方向的重力分量，从而延长飞行时间，增加飞行距离。

在弹道纵向平面内，火箭弹沿速度矢量方向的受力分析，如图2所示。

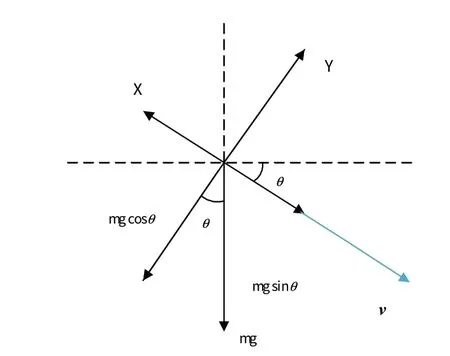
图2 火箭弹在速度矢量方向的受力分析Fig.2 Force analysis of rocket in the direction of velocity vector

从能量角度分析，因高度降低所产生的势能转化成动能和克服空气的阻力，动能的增加势必加快高度的降低，这对增程而言是不利的。因此，将势能尽可能地用来克服空气阻力，维持动能不变或缓慢减小是1种增加射程的有效方法。

由图2受力分析可知，速度是由切向合力控制，高度的降低是由空气作用力和重力两者的合力控制。控制速度变化的切向合力最小，以及控制弹道倾角变化的法向合力最小，即可达到缓慢下降及速度缓慢减小的目的。将上述理论转化为数值表达式，为更易实现这一方法，采用标量的合力之和来替换矢量合力。为避免各合力出现负值的情况，对各合力做绝对值运算。整合以上理论，如式（1）：

式（1）中：

X

为空气阻力；

Y

为空气升力；

m

为火箭弹质量；

θ

为弹道倾角；

g

为当地重力加速度，与高度

y

有关。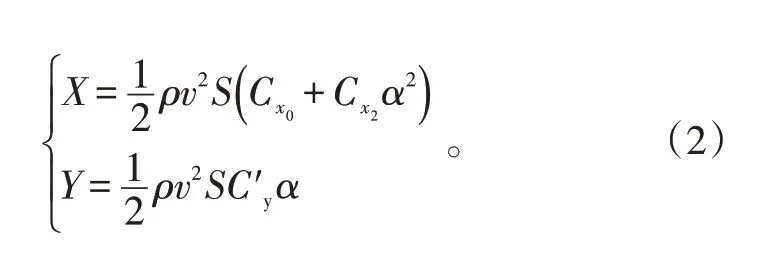

式（2）中：

ρ

为空气密度；

X

为空气阻力；

Y

为空气升力；

S

为弹丸特征面积；

C

为零升阻力系数；

C

为诱导阻力系数；

C

′为升力系数导数；

α

为攻角。火箭弹受力随飞行位置不断发生变化，受飞行稳定性及修正装置等的限制，此处的合力最小为优化问题，须通过优化方法获取。为此，本文提出实时优化的算法以解决这一问题。将优化算法嵌套在弹载计算机程序中，每隔

T

时刻，接收并处理火箭弹的位置及速度信息，求解出采样时刻的最优攻角值，再转化成修正指令，控制舵翼偏转，实现增程目的。

1.2 弹道模型及方程建模

通过对火箭弹增程原理分析，结合原火箭弹特点，总结滑翔增程火箭弹弹道特点如下。

1）主动段。该段弹丸受重力、空气动力及发动机推力作用，受推进剂燃气推动作用，弹丸做加速运动。发动机停止工作后，弹丸达到最大速度。

2）被动段。该段弹丸仅受空气动力和自身重力作用，与无控弹的弹道解法一致。

3）控制段。在弹丸到达弹道顶点附近时，打开舵机。在电机驱动下，舵翼按照舵机指令进行偏转，空气作用力随之发生改变，进而达到调整姿态、修正弹道的作用。

根据以上弹道特点描述，飞行弹道特性模拟图，如图3所示。

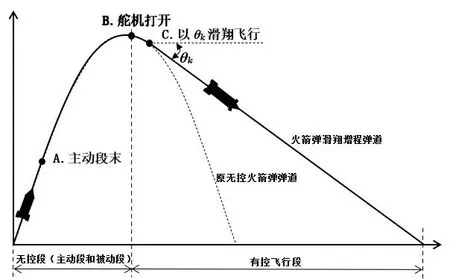
图3 滑翔增程火箭弹弹道模拟图Fig.3 Ballistic simulation diagram of glide extended range rocket

依据前文分析，本文只研究有控弹箭在纵向平面的运动，由于采用卷弧尾翼，弹丸旋转速度会降低，飞行至控制段时近似看作无旋运动，即忽略弹箭绕质心的转动，只研究弹箭质心的运动。由此，纵向平面可操纵质点方程组如下：

2 优化算法建模

2.1 基于单纯形的攻角优化建模

单纯形法（Simplex）是1962 年由Spendley、Hext和Himsworth 提出，再由Nelder 和Mead 于1965 年改进，故又称为NM 算法。它是1 种不使用导数求解无约束极小化问题的直接搜索方法。相比最优化方法中的解析法，此法仅需要相关函数值信息，就可寻找最优解。不同于其他优化的算法，它从最初构造的单纯形，不断替换最大值点，构造更适合寻优的新单纯形。基本原理如下：

在

n

维空间中，以

n

+1 个顶点构成一个单纯形(

x

,

x

,

x

,…,

x

)。并将单纯形中各顶点代入到目标函数中求解函数值。记各函数值中最小值为

f

(

x

)，最大值为

f

(

x

)。并求除最大值以外各点的重心，及最大值顶点关于重心的反射点，依据反射点函数值的大小选择延伸、收缩或压缩，得到新的较好顶点并替换原单纯形中最大值顶点，构造新的单纯形。通过反复求解较小点来替换新单纯形中最大值顶点，迭代单纯形，逼近极小值点。单纯形中重心、反射点、延伸点、收缩点、压缩点以及精度的计算公式如下：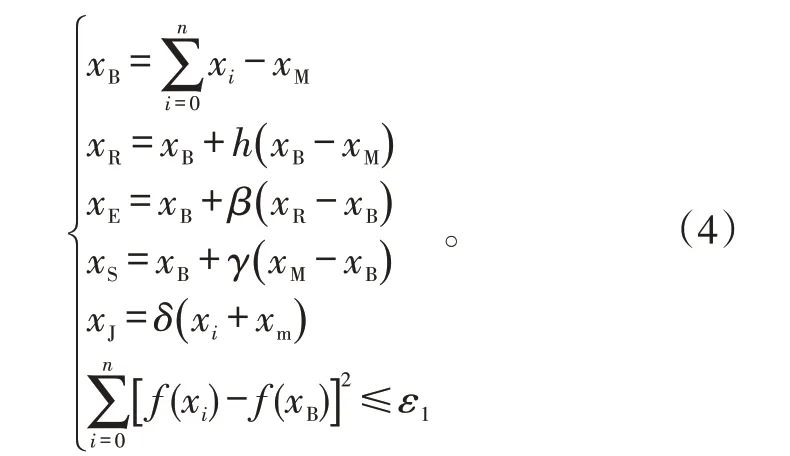

式（4）中：

x

为单纯形顶点；

x

为最大值顶点；

x

为最小值顶点；

x

为重心；

x

为反射点；

x

为延伸点；

x

为收缩点；

x

为压缩点；

h

为反射系数；

β

为延伸系数；

γ

为收缩系数；

δ

为压缩系数；

ε

为计算精度。

2.1.1 选取设计变量

依据公式（1）分析，为获取采样时刻最优攻角，实时弹道优化以采样时刻弹道诸元作为优化输入量，以平衡攻角为优化变量。随采样时刻的更新进行实时优化。设计变量

Γ

见式（5）。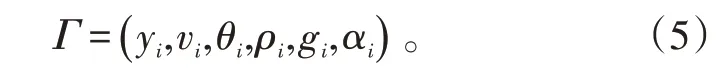

式（5）中：

y

为火箭弹采样时刻高度；

v

为采样时刻速度；

θ

为采样时刻弹道倾角；

ρ

为采样时刻空气密度；

g

为采样时刻的重力加速度；

α

为采样时刻待优化的攻角。

2.1.2 建立目标函数

基于公式（1）分析，将采样时刻的位置和速度信息作为优化输入量，以采样时刻合力最小值为目标函数。结合式（1），目标函数

F

见式（6）：

2.1.3 添加参数约束

攻角的取值，取决于弹箭物理参数及舵机的修正能力，更重要的是不能影响飞行稳定性，这限制了攻角只能在一定范围内变化，见式（7）：

式（7）中：

α

为攻角最小值；

α

为攻角最大值。

2.1.4 算法终止条件

单纯形算法优点是寻优效率高，能快速迭代到最优解附近；缺点是在最优点附近收敛速度较慢。而实时修正的核心即时效性，短时多修，因此对于精度要求并不是很高。为了更好满足实时解算要求，缩短算法终止时间，本文在原算法基础上再增添终止条件，以连续3 次输出迭代优化值之差小于迭代误差

ε

作为终止条件。双重终止条件能有效缩短迭代时间。迭代误差

ε

见公式（8）：

式（8）中：

ε

为迭代误差；

x

为第

i

次迭代结果；

x

为第

i

-1次迭代结果。

2.1.5 单纯形法优化攻角流程

1）设定控制段采样时刻

T

=0.1 s，获取采样时刻的火箭弹位置和速度信息。统一设定待优化的攻角初始值为0。并设定优化函数中的参数值：初始步长、反射系数、收缩系数、压缩系数及计算精度。

2）将初始攻角值及采用初始步长获取的新攻角值代入插值函数中，分别插值计算出当前攻角及马赫数下的气动力参数，并将气动力参数值代入目标函数中，求解当前目标函数值。

3）将2）中得到的目标函数值返回到优化算法中，确定最小值顶点

x

及最大值顶点

x

，并计算重心、反射点。4）通过对反射点的函数值求解，选择延伸处理、收缩处理或压缩处理。使目标函数更小的点为新的单纯形顶点，返回并替换步骤3）中的

f

( )

x

，重新确定新单纯形的最大值顶点及最小值顶点，重复以上步骤，反复迭代新单纯形，直至满足计算精度为止。

5）将优化算法得到的攻角值与式（6）比对，将不在攻角设定范围的攻角值进行输出限制或替换。最后输出攻角，作为当前火箭弹飞行的控制量。直至得到下1 个最优攻角。通过这种交替优化解算方法，获取控制全段的最优攻角值。

2.2 SIMULINK建模仿真

工程上常用C语言求解弹道，这对编程能力要求高。SIMULINK 是将MATLAB 的相关函数进行模块化封装，对使用者来说要求低、易上手，对于所有设定的参数均可实时读取，通用性高，可视性强，已成为学者和工程师求解弹道的常用软件。本文采用SIMULINK 仿真平台进行滑翔增程火箭弹模型建立与仿真分析。

依据滑翔增程弹的弹道特性，整个弹道模型由弹道初始模块、气象标准模块、气动力模块、弹道方程组模块、优化算法模块组成。各模块内部以子模块或函数组成。滑翔增程火箭弹弹道解算框图，如图4所示。

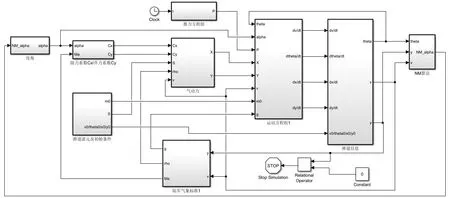
图4 滑翔增程火箭弹弹道解算框图Fig.4 Diagram of ballistic calculation for glide extended range rocket

2.2.1 弹道初始化模块

在SIMULINK中设置滑翔增程火箭弹的参数，见表1。

表1 火箭弹参数Tab.1 Rocket parameters

2.2.2 NM优化算法模块

依据算法，将函数的所有输入的参数封装到函数模块中，该函数模块包括3 个函数：气动力插值函数，目标函数及单纯形优化函数。NM子模块中的单纯形优化算法函数模型，见图5所示。

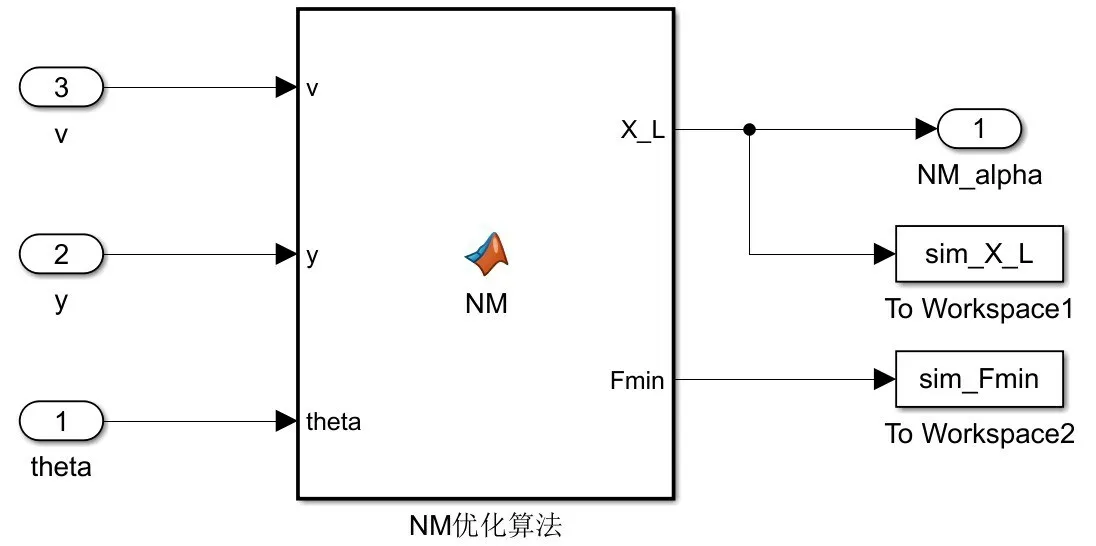
图5 单纯形优化算法函数模块Fig.5 Function module of simplex optimization algorithm

本文火箭弹模型，依据舵机修正能力及飞行稳定性，设定攻角取值范围为[0 °,8°] 。单纯形优化算法是一种无约束优化，对于优化结果超出优化变量约束范围的，将以攻角最值输出。也就是优化结果大于8°则取8°，小于0°则取0°。

2.2.3 气动力参数模块

本文采用DATCOM 软件获取滑翔增程火箭弹的气动参数。将建好的滑翔火箭弹模型的弹体参数（见表1）及舵机参数编制文件，设定不同马赫数和攻角值，分别计算原火箭弹气动参数，以及添加舵机后的滑翔火箭弹的气动参数。根据滑翔增程火箭弹弹道特点，在主动段和被动段使用无舵翼气动力参数，打开舵机后使用有舵翼的气动力参数。

3 仿真结果及分析

由于滑翔增程弹的舵机是在顶点附近打开的，因此弹道的主动段和被动段均与原火箭弹相同。忽略无控段受外部随机干扰造成的攻角变化，采用零攻角仿真无控段。本文采用SIMULINK 自带算法（ode45），四阶龙格库塔解算弹道。

设定滑翔增程火箭弹初始条件是：

θ

=50°，

v

=50 m/s，

x

=0，

y

=0。将初始条件设置到SIMULINK模块中，设置积分步长与采样时刻同为0.1。设置程序终止条件为

y

＜0。优化函数算法中各参数取值分别为：初始步长

h

=2，延伸系数

β

=2，收缩系数

γ

=0.5，压缩系数

δ

=0.5，计算精度

ε

=0.05，迭代终止精度

ε

=0.001。

考虑到火箭弹飞行中受到（风等）扰动，以及弹载计算机获取的位置坐标误差及地磁测量姿态误差等因素，转化各种误差因素为攻角的响应白噪，即在实时优化后的攻角值上随机添加[ ]-0.2°,0.2° 的偏差量。

图6为零攻角下原火箭弹的弹道曲线。图7为有噪与无噪的优化弹道对比图。图8为有噪和无噪的优化攻角对比图。图9 为实时攻角下的优化目标函数值。图10是在原单纯形算法下，对不同采集时刻的弹道信息分别进行实时优化的迭代次数与优化攻角的对比图。

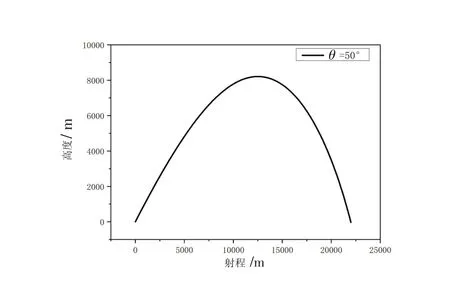
图6 零攻角火箭弹弹道Fig.6 Ballistic curve of the rocket at zero angle of attack

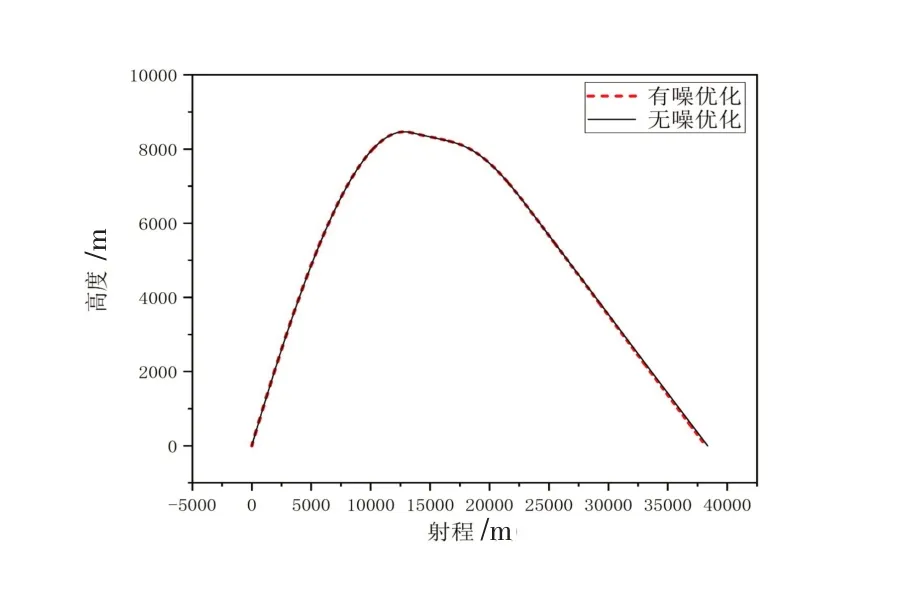
图7 实时优化后的弹道Fig.7 Ballistic curve of the rocket after real-time optimization

图8 实时优化后的火箭弹攻角Fig.8 Angle of attack of the rocket after real-time optimization

图9 实时优化下的目标函数值Fig.9 Objective function value under real-time optimization

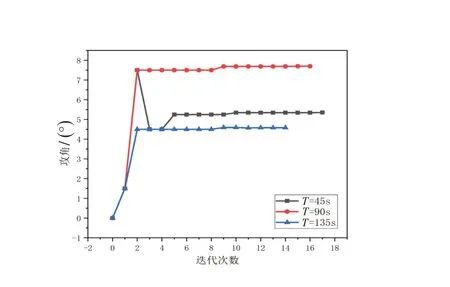
图10 不同时刻下迭代次数与优化结果Fig.10 Number of iterations and optimization results at different moments

图6、7 对比表明，在射角50°、零攻角下的原无控火箭弹的射程仅22 000 m。而采用本文提出的改进单纯形优化算法解算实时攻角，无噪射程为38 344.87 m ，有噪射程为38 205.04 m ，偏差仅139.83 m，无噪下增程率达到74.3%。说明此优化方法能有效增加火箭弹的射程。

图7～9表明，在相同初始条件下，无噪和有噪解算结果相差甚小，实时解算具有较高的抗噪性。实时解算的最优攻角变化平稳，并无大的突变，对于舵机修正而言，易于实现。此改进算法能有效地应用于弹载计算机上。

图10 表明，虽然达到原算法的计算精度，但迭代次数较多，耗时较长，不利于快速多次的实时修飞理念。

通过表2 的数据比对，原算法实时求解的时间较长，从而使舵机修正的时间间隔延长。而随着修正间隔时间的增加，精度必然降低。采用改进后的算法，迭代次数更少，而且优化结果与原算法相差较小。改进算法能有效地缩短间隔时间，增加修正次数，更能满足实时解算的要求。

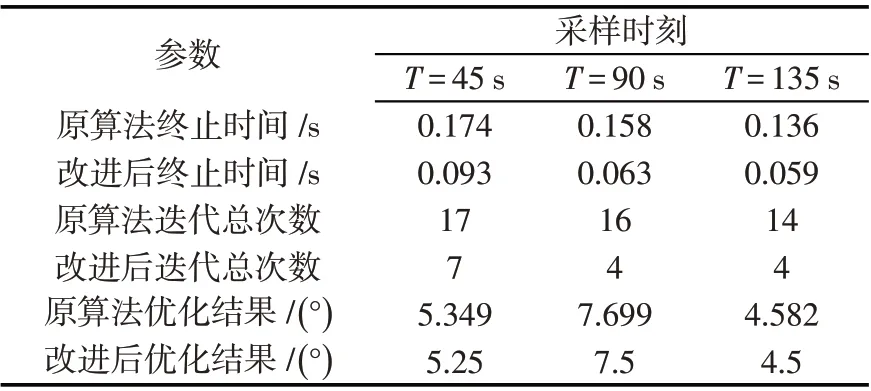
表2 原算法和改进算法寻优结果对比Tab.2 Comparison of optimization results between the original algorithm and the improved algorithm

4 结论

针对火箭弹增程问题，在理想滑翔状态理论基础上，分析并提出了基于改进单纯形算法的实时优化攻角的增程方法，通过在SIMULINK仿真平台上建立弹道模型并仿真分析，得出以下结论：

1）与无控火箭弹射程相比，基于改进单纯形优化算法的增程方案使得火箭弹增程率达到74.3%；

2）改进后的单纯形优化算法更适合弹载计算机实时优化。