无人艇集群协同定位算法误差分析

张琳琳，王海滨

（1.陆军军事交通学院，天津 300130；2.海军航空大学，山东烟台 264000）

无人艇自身具有动力，可操控，能够负载多种功能设备，完成多种任务，并且能够重复使用。此外，无人艇还具有成本低、损耗低、零伤亡、隐蔽性好、机动灵活等优势，其已在军事、民用以及科学研究等多个领域被广泛使用。无人艇由于载荷有限，一般采取多艘无人艇组成无人艇集群方式协同完成各种复杂任务。以无人艇集群协同完成任务的1个基本前提为无人艇集群中的每1个成员都能够获得高精度的定位信息。

传统定位方式中，惯性导航系统具有自主性好，全天候，能给出所需的位置、速度、姿态全量导航信息等优势，但是其误差随着时间累积会不断增大，且小型惯导的精度相对较低。卫星导航系统具有小型化、高精度等优势，但是由于其信号弱，容易受到外部电磁环境的干扰或受到建筑物、植物等的阻碍，自主性和可靠性较差。

为了弥补惯性导航系统和卫星导航系统的不足，一般采用数据链对无人艇集群之间的距离进行精确测定，实现相对位置计算，从而实现无人艇集群间的协同定位。

由于无人艇的广泛使用，无人艇集群间协同定位问题也受到了极大的关注。学者对怎样综合利用惯导、卫星导航和数据链提升协同定位精度进行了广泛研究。总体来说，数据链的协同定位对无人艇协同定位的性能影响较大，为此本文对基于数据链的协同定位误差进行了较为全面地分析，以期对无人艇集群协同导航应用技术发展提供参考和借鉴。

1 基于数据链协同定位原理

对于无人艇集群来说，基于数据链协同定位，一方面能够将具有高精度导航信息平台的导航精度辐射到搭载低精度导航传感器的平台；另一方面，当系统中某个平台的导航系统被毁坏后，无导航系统的平台可通过基于数据链协同定位方式获得自身位置信息，保障任务得以继续执行。在协同定位系统中，一般选取具有高精度导航信息的平台作为协同定位基准，通常称之为源节点。同时，选择一定位置作为相对坐标原点，通过具有高精度导航信息平台估算出其相对所选原点的位置关系，并利用高精度惯性导航系统不断推算自己在所定义坐标系中的位置，利用数据链将位置坐标、地理位置、信号发射时间等数据（即精确参与定位消息，文中称PPLI）广播出去。其他导航系统精度较低的集群中的平台通过接收该PPLI 便可计算出该PPLI隐含的坐标原点的地理位置，从而估出自己在该坐标系下的坐标位置。

如图1所示，坐标系确定后，无人艇集群中其他导航系统精度较低的平台通过测量PPLI的到达时间，计算出其与源节点之间的伪距，在通过多边形定位法对自身位置进行估算。

图1 无人艇集群示意图Fig.1 Diagram of unmaned surface vehicle cluster

基于数据链协同定位的计算方程为：

式（1）中：

ρ

为导航系统精度较低的平台与第

i

个源节点位置之间的实际距离；

x

、

y

、

z

为导航系统精度较低的平台的位置坐标；

x

、

y

、

z

为第

i

个源节点的位置坐标；

ρ

为观测到的导航系统精度较低的平台与第

i

个源节点位置之间的伪距；

c

为光速；

t

为导航系统精度较低的平台通过接收第

i

个源节点PPLI观测的到达时间；

b

为导航系统精度较低的平台与第

i

个源节点之间的时钟偏差；

N

为测量误差之和。通过测量导航系统精度较低的平台与多个源节点之间的伪距，组成协同定位方程便可确定导航系统精度较低的平台的位置坐标和时间偏差

b

。

2 基于数据链协同定位误差分析

根据上述定位原理，可知影响基于数据链协同定位精度因素有时间偏差、各个源节点的位置误差和测量误差等。其中，时间偏差可通过增加源节点的方式，与导航系统精度较低的平台的位置一同进行估算，这样，对导航系统精度较低的平台的定位精度影响较低。而导致量测信息产生误差的因素较多，不易建模，且对定位精度影响较高。为此，本文对上述误差的种类、特点、性能影响以及解决方法等进行研究，如下所示：

一是源节点位置误差。源节点的位置精度取决于无人艇集群的配置，对导航系统精度较低的平台的定位精度影响较大。二是源节点的时间质量。源节点的时间质量将对到达时间的测量精度造成影响，从而影响导航系统精度较低的平台的定位精度。三是无人艇集群的几何精度因子。几何精度因子取决于导航系统精度较低的平台与选定的源节点的相对几何关系，取决于无人艇集群队形等因素，对导航系统精度较低的平台的定位精度影响较大。四是到达时间的量测误差。该误差主要取决于硬件、接收信噪比以及数据链的信号体制。五是无线信号传播影响。基于数据链的协同定位算法中，伪距测定是通过无线信号传播时间进行估算的。无线信号在传播过程中受到大气影响产生折射等，从而导致通过测得无线信号传播时间计算的伪距与2节点间真实距离存在一定的误差。

假设低精度或者导航系统故障的无人艇（以下简称S艇）在第k次数据更新时刻的坐标为( )

x,y,z

，高精度或者导航系统正常的无人艇（以下简称M 艇）在第k次数据更新时刻的位置为( )

x,y,z

，2者之间的距离为

r

，距离方程为：

式（6）关于S艇位置

X

的偏微分方程为：

3 协同定位误差影响仿真验证

为了深入剖析基于数据链协同定位误差的影响，本文对源节点位置精度、几何精度因子、伪距测量精度（包括源节点时间质量、达到时间测量误差和无线信号传播影响等）对协同定位误差影响进行了仿真分析。

3.1 源节点位置精度影响分析

为了更加具体说明源节点位置精度对导航系统精度较低的平台协同定位精度的影响，本文仿真分析了几何精度因子为4 左右，测试周期为3 s，伪距测量精度为30 m，源节点位置误差为10 m、20 m、50 m、100 m、200 m、500 m 时，导航系统精度较低的平台协同定位误差结果，如图2 ～图7所示。

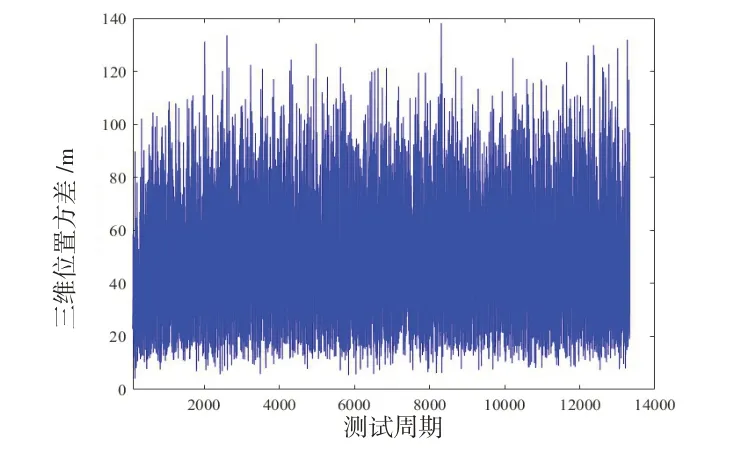
图2 协同导航定位误差（源节点误差10 m）Fig.2 Location error of cooperative navigation（source node error is 10 m）

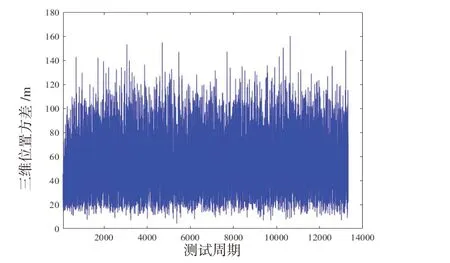
图3 协同导航定位误差（源节点误差20 m）Fig.3 Location error of cooperative navigation（source node error is 20 m）

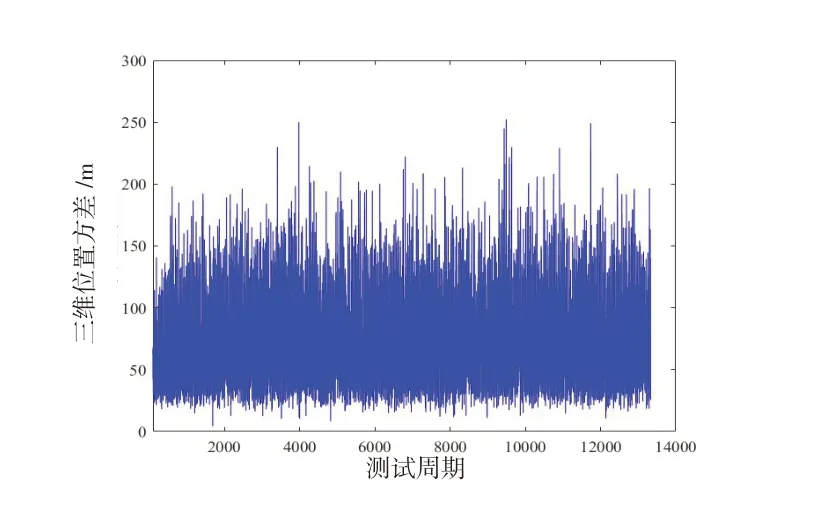
图4 协同导航定位误差（源节点误差50 m）Fig.4 Location error of cooperative navigation（source node error is 50 m）

图5 协同导航定位误差（源节点误差100 m）Fig.5 Location error of cooperative navigation（source node error is 100 m）

图6 协同导航定位误差（源节点误差200 m）Fig.6 Location error of cooperative navigation（source node error is 200 m）

根据图2 ～图7所示，表1统计了在上述6种情况下，导航系统精度较低的平台协同定位均方误差。

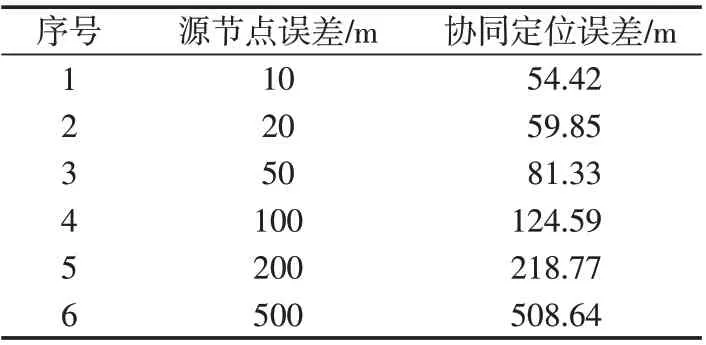
表1 源节点误差对协同定位精度影响统计Tab.1 Influence of source node error on cooperative location accuracy

图7 协同导航定位误差（源节点误差500 m）Fig.7 Location error of cooperative navigation（source node error is 500 m）

从表1可知，随着源节点位置误差不断增多，导航系统精度较低的平台协同定位误差不断增大，导航系统精度较低的平台协同定位误差增量比源节点位置误差增量要小。

3.2 几何精度因子影响分析

本文仿真分析了伪距测量精度为30 m，源节点位置误差为10 m，无人艇集群几何精度因子分别为2和4时的导航系统精度较低的平台协同定位结果。其中几何精度因子为4的导航系统精度较低的平台协同定位误差如图2 所示；几何精度因子为2 的导航系统精度较低的平台协同定位误差，如图8示。

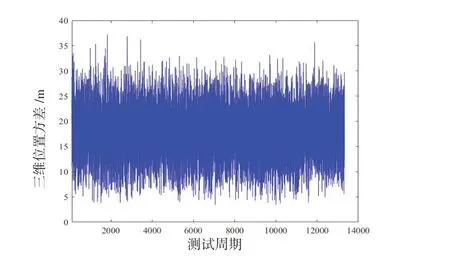
图8 协同导航定位误差（几何精度因子为2）Fig.8 Location error of cooperative navigation（geometic precision factor is 2）

从图8可知，当几何精度因子为2时，协同定位均方误差为18.72 m。对比图2和图8可知，当几何精度因子增大时，导航系统精度较低的平台协同定位误差随着增大，几何精度因子增大1倍，导航系统精度较低的平台协同定位误差增大不止1倍。可见几何精度因子对导航系统精度较低的平台协同定位精度影响较大。

3.3 伪距测量精度影响分析

本文仿真分析了几何精度因子为4，源节点位置误差为10 m ，伪距测量误差分别为30 m 、50 m 、100 m、200 m、500 m 时，导航系统精度较低的平台协同定位误差，如图2、图9 ～图12 所示。表2 给出了5种伪距测量误差情况下，导航系统精度较低的平台协同定位均方误差统计结果。

表2 伪距测量误差对协同定位精度影响统计Tab.2 Influence of pseudorange measurement error on cooperative location accuracy

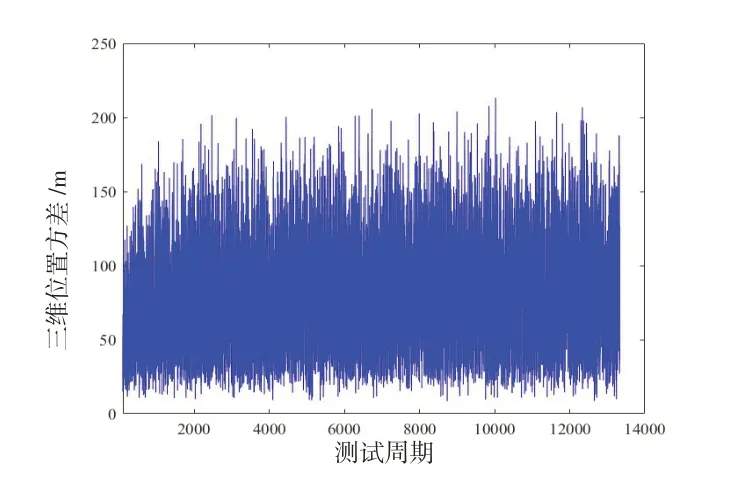
图9 协同导航定位误差（伪距测量误差为50 m）Fig.9 Location error of cooperative navigation（pseudorange measurement error is 50 m）

图10 协同导航定位误差（伪距测量误差为100 m）Fig.10 Location error of cooperative navigation（pseudorange measurement error is 100 m）

图11 协同导航定位误差（伪距测量误差为200 m）Fig.11 Location error of cooperative navigation（pseudorange measurement error is 200 m）

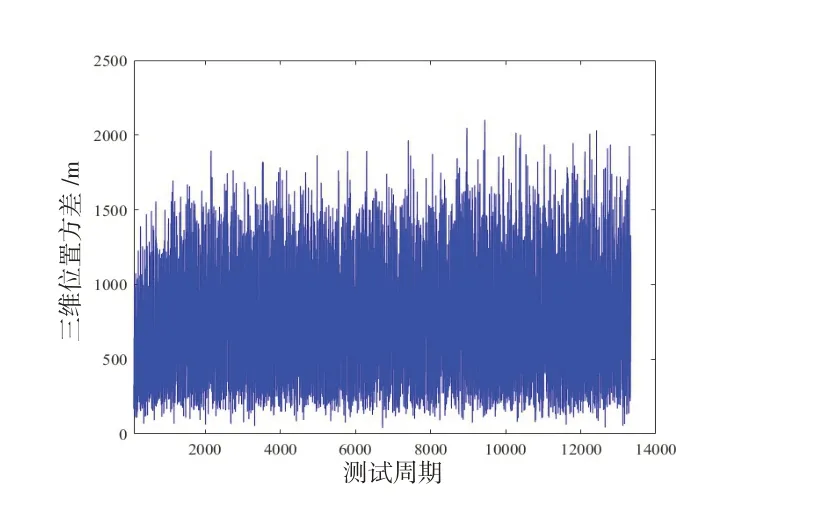
图12 协同导航定位误差（伪距测量误差为500 m）Fig.11 Location error of cooperative navigation（pseudorange measurement error is 500 m）

从表2可知，随着伪距测量误差不断增多，导航系统精度较低的平台协同定位误差也随之增多，导航系统精度较低的平台协同定位误差增大幅度比例与伪距测量误差增大比例相差无几。

4 结论

目前，对无人艇集群的研究正逐渐从理论研究转换到应用研究。本文着眼无人艇集群在未来应用中的实际需求，分析了无人艇协同定位误差种类和特点，并针对影响较大的3 个因素进行了仿真分析。从仿真分析结果可知，无人艇集群伪距测量误差和几何精度因子对协同定位误差有较大影响，源节点位置误差影响相对较小。因此，在源节点选择时，应该有效选择几何精度因子交换的源作为源节点。而协同定位误差的大幅度减低，有赖于采用优良的信号体制等技术，从而使伪距测量误差尽可能减小，从而极大提高协同定位精度。