具有非局部反应声学边界条件和边界时滞的波动系统稳定性
李静,梁晓珍
(山西大学 数学科学学院,山西 太原 030006)
0 引言
令Ω 是Rn(n≥2)中开的有界连通区域,且具有光滑边界Γ。 假设Γ0和Γ1是Γ 的具有正测度的不相交闭子集且满足Γ=Γ0∪Γ1。 本文考虑以下具有声学边界条件的波动系统初边值问题:
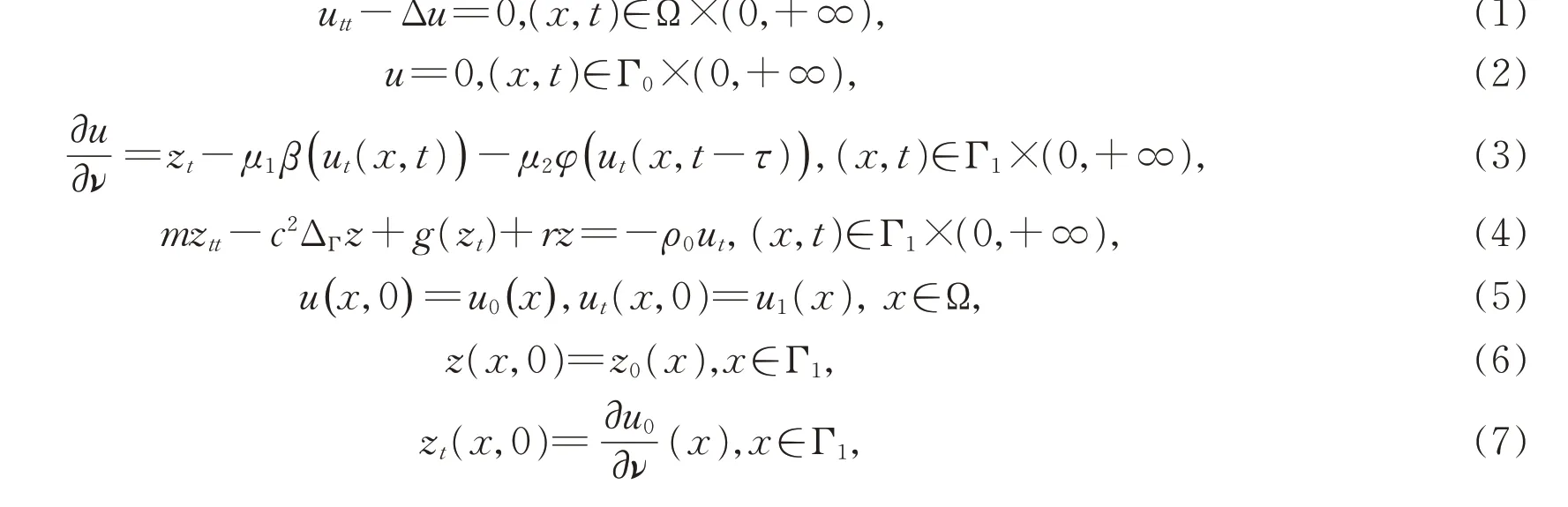

系统(1)—(8)是一个具有声学边界条件的波动系统,这类模型在实际应用研究中多用于噪声的控制和抑制研究。Morse 和Ingardy[1]首先将这类声学边界条件引入到了波动系统的控制研究中,之后Beale 和Rosencrans[2]进一步改进和发展了这类声学边界条件。本文中的边界条件(4)是一类具有非局部反应边界的声学边界条件。它描述了边界Γ1上的点在波的附加压力作用下类似于弹性膜的振动行为,而非局部反应边界则刻画了边界Γ1上的各点间的振动是相互影响的。如果假设Γ1上的每一个点在附加压力作用下的振动行为都像弹簧一样,并且相邻的点之间没有横向张力,则(4)中的项“c2ΔΓz”将消失,此时称边界Γ1是一类传统的局部反应的。显然,本文所研究的非局部反应边界条件(4)推广了经典的局部反应声学边界条件,能够更加准确地刻画弹性边界的实际振动。
对于具有声边界条件的波动方程,局部反应边界的情形已经被许多学者进行了广泛地研究,详见文献[3-5]。近年来,具有非局部反应边界的声学边界条件也引起了许多学者的关注,获得了一些相关的研究结果。可参阅文献[6-9]。在文献[10]中,作者考虑了一类具有非局部反应声学边界的波动系统,证明了即使内部阻尼的作用范围是局部的,该波动系统的一致稳定性仍然成立。在文献[6]中,作者研究了具有声学边界条件的载流子型波动方程,在非局部反应边界条件下,证明了该方程混合问题的整体解的存在性、唯一性和渐近稳定性。
时滞是自然界中的一类普遍现象,也是导致系统不稳定的原因之一。因此,对具有时滞扰动的偏微分系统控制问题的研究一直以来受到学者们的广泛关注,详见文献[3,5,11,12]。在文献[5]中,作者将时滞效应引入到具有声边界条件的波动系统的稳定性研究中,研究了一类具有声学边界条件和时滞的非线性变系数波动系统,获得了该系统能量的一般衰减率。
据我们所知,目前有关具有时滞效应的声学边界问题的研究主要集中于局部反应边界的情形,对于非局部反应边界的研究还很少,尤其是时滞效应出现在交界面Γ1处的还几乎未见到过。而本文则对这类模型的稳定性进行了探究,所获得的结论将目前已有的关于时滞声学边界模型的研究推广到了非局部反应边界的情形。本文主要使用乘子法和能量估计方法获得此类系统能量的一般衰减率。考虑到边界耗散,还将使用边界上的迹定理,从而减少对边界条件的几何限制。
1 符号假设及主要结论
1.1 符号假设
设Ω,Γ0,Γ1是引言中定义的集合。记空间L2(Ω)和L2(Γ1)中内积和范数分别如下:
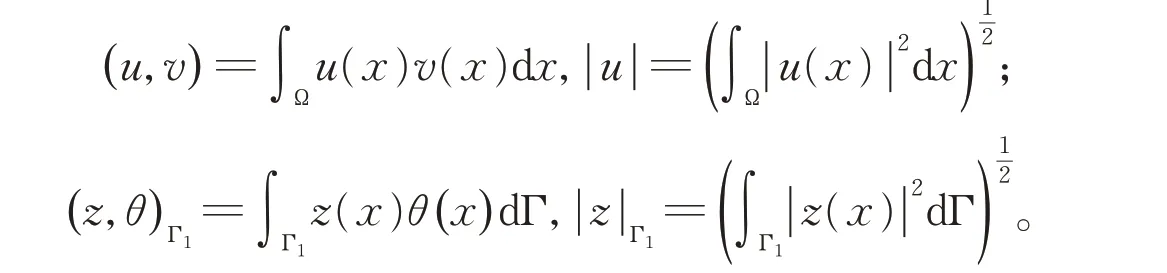
定义集合V={u∈H1(Ω);u=0a.e.(x,t)∈Γ0}。 显然Poinearé 不等式在V中成立,即存在一个正常数k使得|u|≤k|∇u|。因此我们可以赋予V如下的内积和范数:

注意到Γ1是一个没有边界的紧致流形,可以分别赋予空间H1(Γ1)和Η2(Γ1)以下范数:
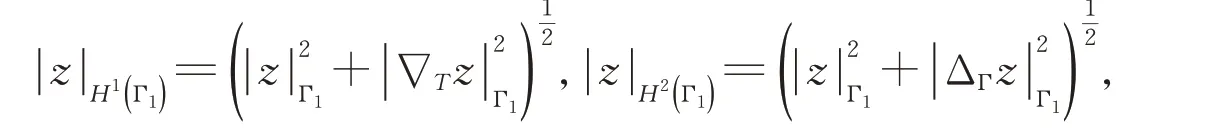
其中∇T是切梯度。
1.2 假设条件
为了获得系统(1)—(8)的一致稳定性结论,我们引入一些基本的假设条件。
假设1 (1)令函数β,g是C1(R)类的单调递增函数,且满足β(0)=0,g(0)=0,假设存在正常数β1,β2,g1,g2,,使得
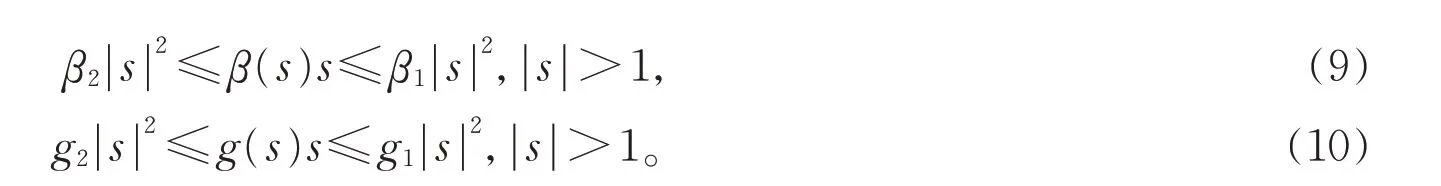
(2)令函数φ是C1(R)类的单调递增的奇函数。假设存在正常数φ0,φ1,使

注记1 由于φ是一个递增的奇函数,易得

假设3 令x0是Rn中的一个定点,假设(x-x0)·ν≤0,x∈Γ0。
利用Fadeo-Galerkin 方法,可以得到如下系统(1)-(8)的解的存在唯一性结论:
令假设1-3 成立,设u0∈V∩H2(Ω),u1∈V,z0∈H2(Γ1),k0∈V(Γ1×(-τ,0)),则系统(1)—(8)存在唯一的解(u,z),且满足
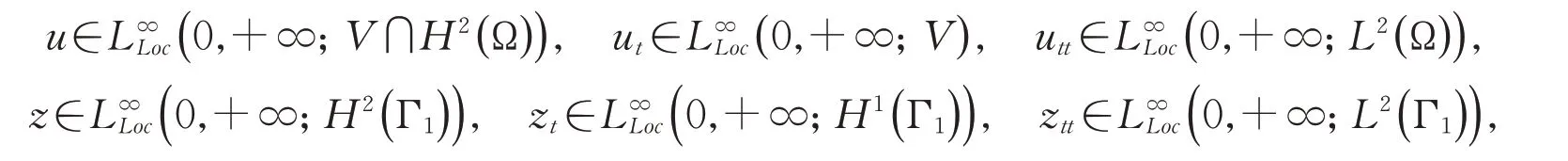
有关上述适定性结论的证明可以参阅文献[5,13]做类似的证明,这里省略。
在假设2 成立的条件下,我们定义系统(1)—(8)的能量如下:
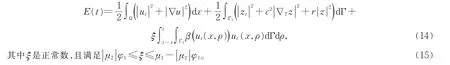
由假设2 可知,这样的ξ是存在的。
为了方便,本文中将能量泛函E(t)中的传统能量部分记为E0(t),即
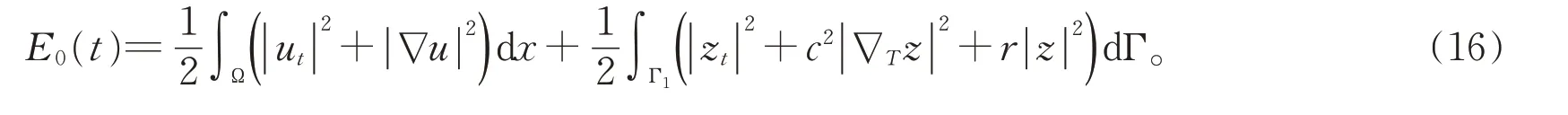
1.3 主要结论
本文主要是研究具有声学边界条件的波动系统(1)—(8)在边界时滞扰动下的一致稳定性。以下是本文的主要结论。
定理1 令假设1-3 成立。对于系统(1)-(8)的解(u,z),存在一个常数T>0,使得
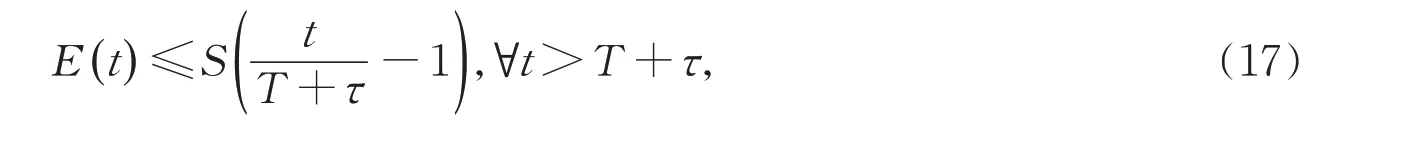
其中S(t)是如下微分方程的解:
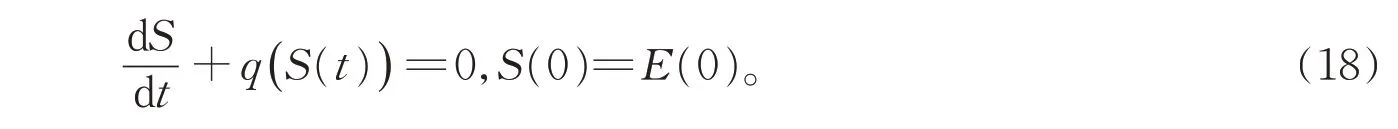
这里q(r)是由(49)-(52)、(54)、(62)给出的连续单调递增函数且函数S(t)一致衰减到零。
2 定理1 的证明
通常,我们只需要对系统的强解进行相关研究。通过经典的稠密性定理,定理1 对于弱解仍成立。
本文中,为研究方便,以下用zt(t),zt(t-τ)分别表示zt(x,t),zt(x,t-τ)。
引理1 令假设1-3 成立。对于系统(1)-(8)的解(u,z),存在一个常数C1>0,使得
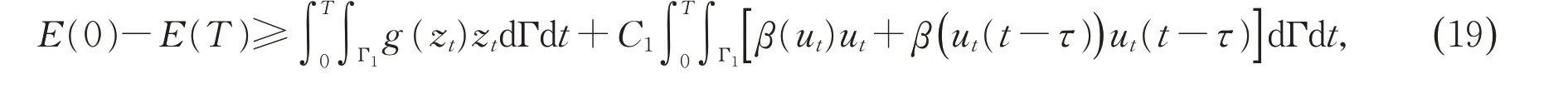
其中常数T≥0。
证明 对系统(1)-(8)的能量泛函E(t)微分,代入相应的边界条件可得:
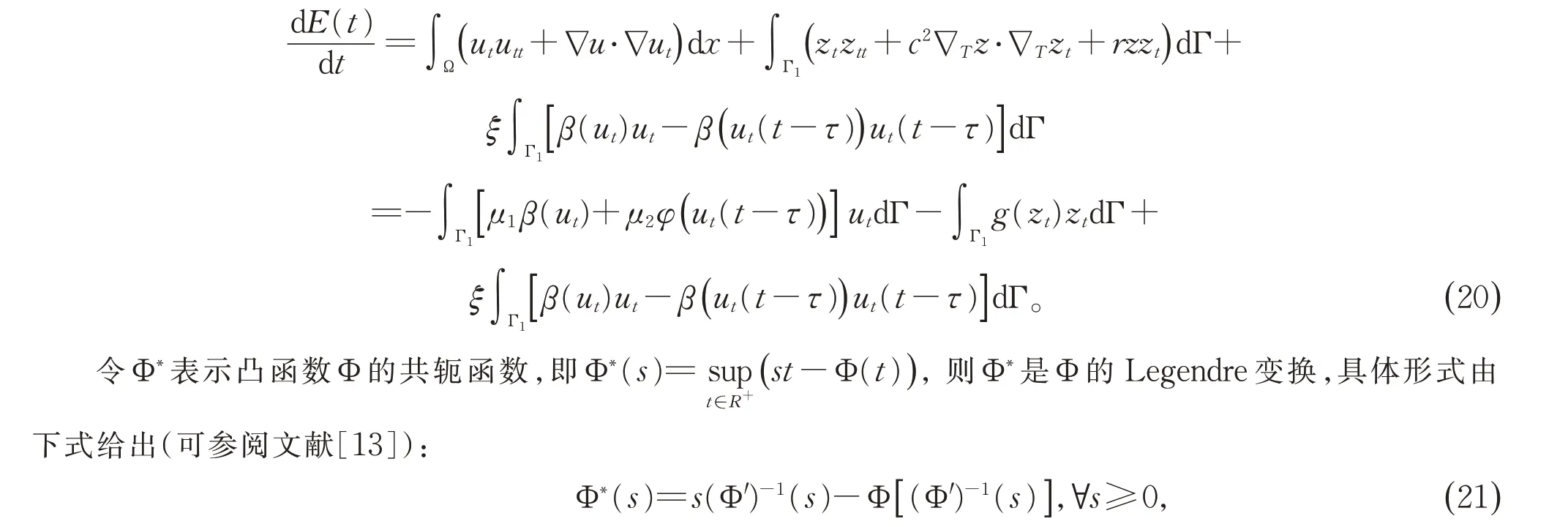
且满足以下不等式

根据本文中Φ 的定义,可知
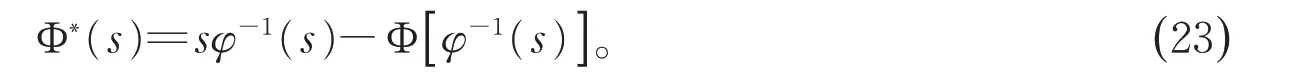
利用上述结论,由假设1 可得
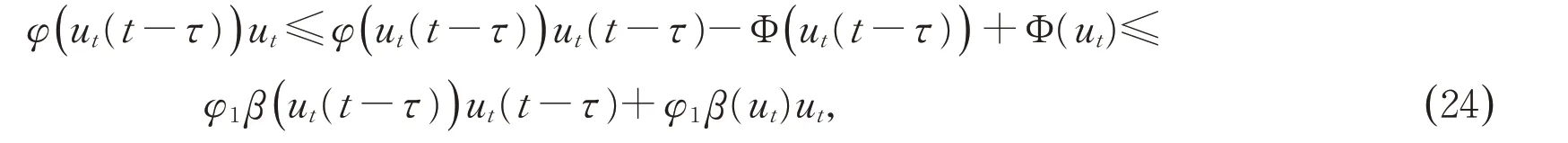
将(23)代入(20)可得

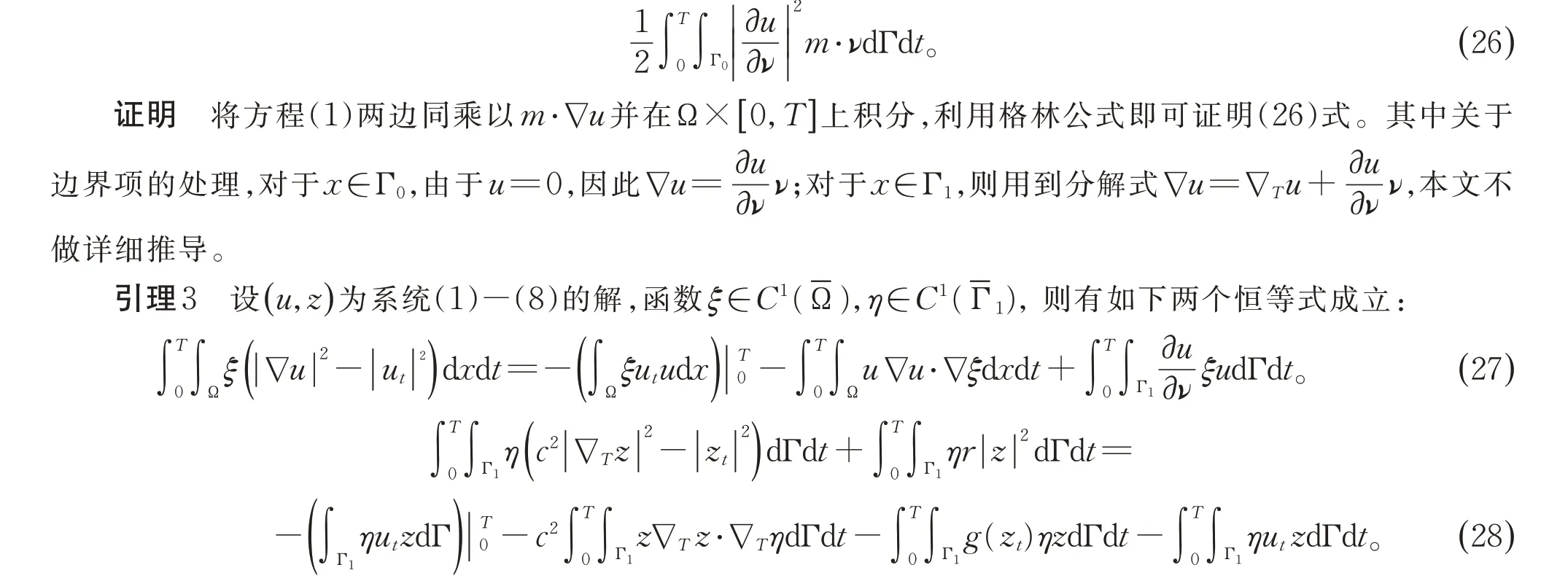
证明 将方程(1)两边同乘以ξu并在Ω×[0,T]上积分,注意到u=0,x∈Γ0,应用格林公式即可得(27)式。
将方程(4)两边同乘以ηz并在Γ1×[0,T]上积分,注意到边界Γ1是一个无边的紧流形,应用格林公式即可得(28)式。引理3 得证。
引理4 在假设1-3 成立的条件下,当T足够大时,系统(1)-(8)的解满足以下能量估计式:
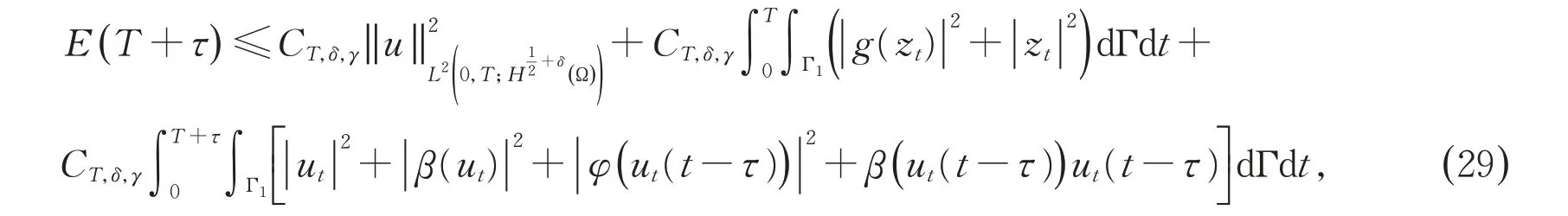
此处以及以下内容中,我们使用常数C>0 来表示与所涉及函数无关的常数,他们在文中不同位置可能表示不同的常数值。
证明 结合乘子恒等式(26)、(27)、(28),代入边界条件(3)可以得到:
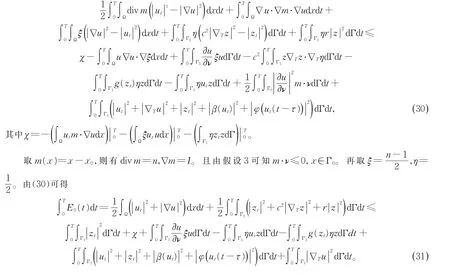

将(39)代入(38)可得
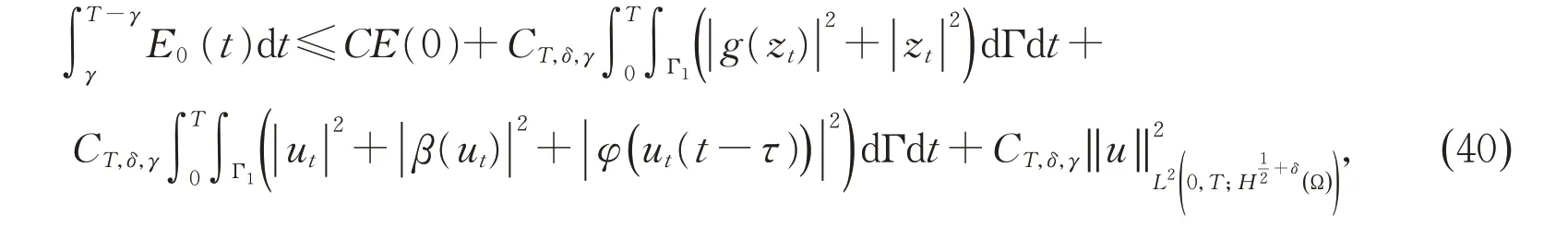
其中用到了E(t)的单调递减性。
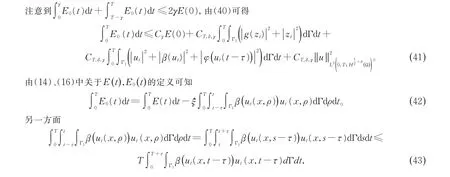
将(43)代入(42)得
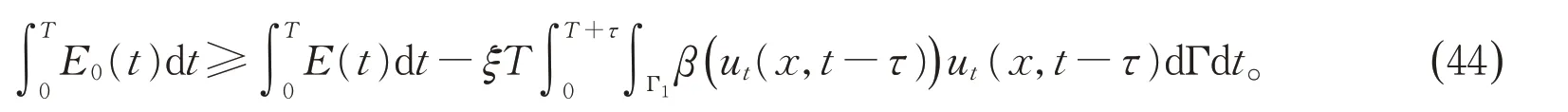
由(20)中关于E(t)的微分可知
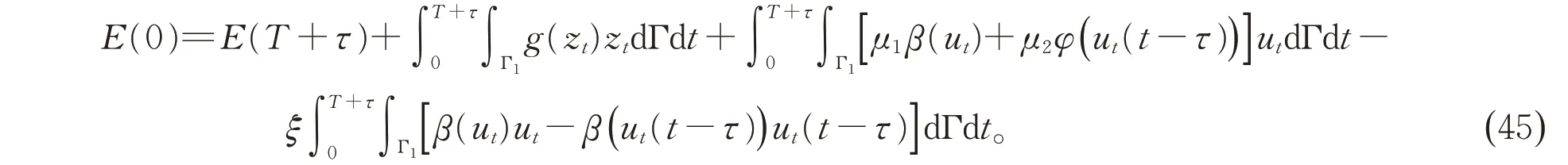
将(41)、(45)代入(44),并且注意到E(t)的单调递减性可得
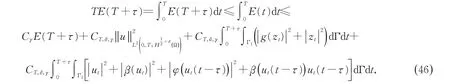
取T足够大,则由(46)式即可推出(29)式。引理4 得证。
能量估计式(29)右边的第一项是一个低阶项,通过紧唯一性可以将此低阶项吸收掉。
引理5 (紧唯一性)令假设1-3 成立。对于系统(1)-(8)的解(u,z),当T>0 足够大时,存在常数C2>0 使 得
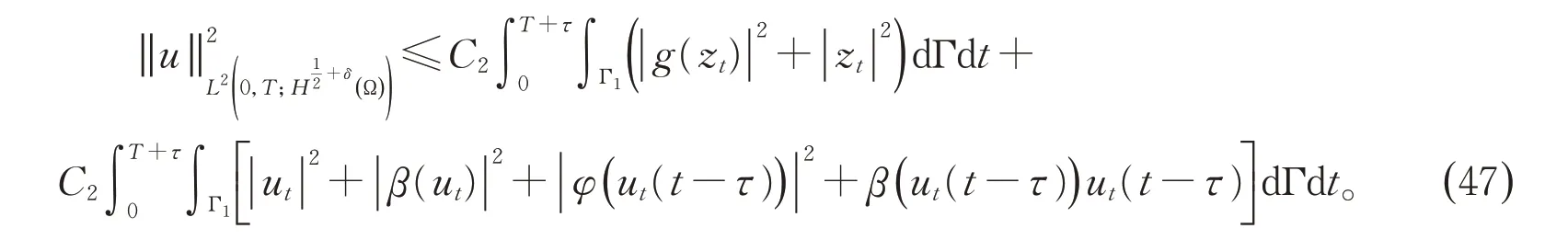
类似于文献[5],通过紧性和唯一性结论可以证明系统(1)-(8)的解满足(47)。这里不再赘述。
结合引理4 和引理5 易得如下能量估计式。
引理6 令假设1-3 成立。对于充分大的常数T>0,系统(1)-(8)的解满足以下能量估计:
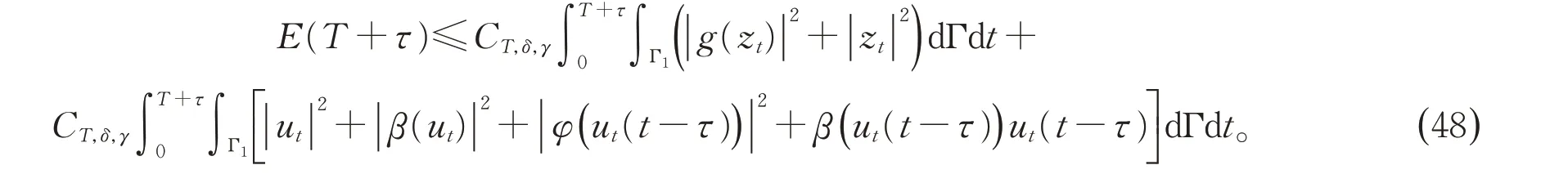
定理1 的证明 类似于文献[8],令h1,h2:[0,+∞) →R是两个严格递增的凹函数且满足h1(0)=0,h2=0 和
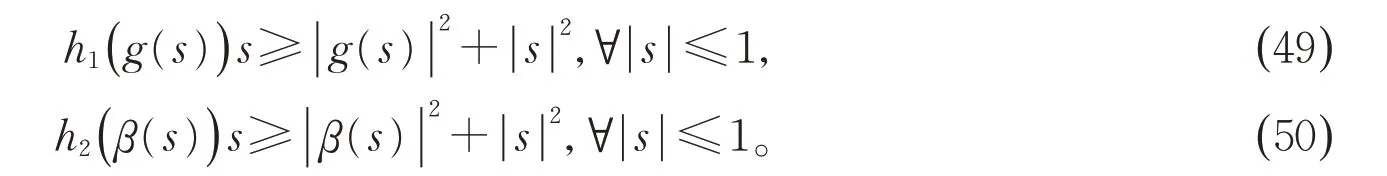
由假设1 可知满足(49)和(50)的函数h1和h2是存在的。
为简洁起见,记Σ1=Γ1×(0,T+τ)。用measΣ1表示Σ1的测度。定义辅助函数h˜1(x)和h˜2(x)如下:

其中C1是由引理1 中确定的正常数,不难看出h˜1(x),h˜2(x)也是单调递增的。
参照文献[5,15]的方法,只需证明:当T>0 充分大时,以下不等式成立:

其中


由假设1 可知
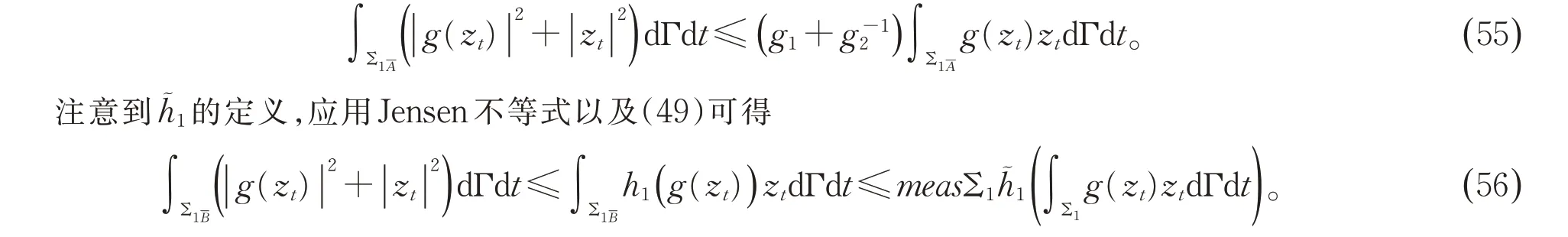
由假设1 还可知
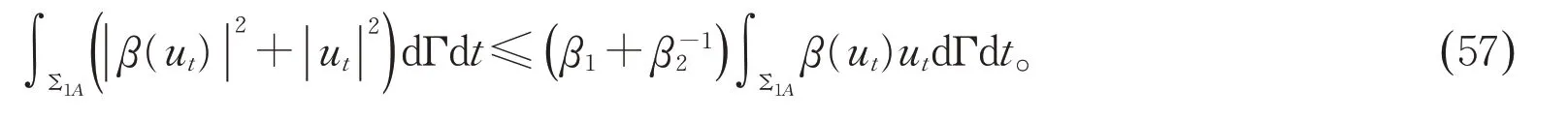
注意到h˜2的定义,应用Jensen 不等式以及(50)可得
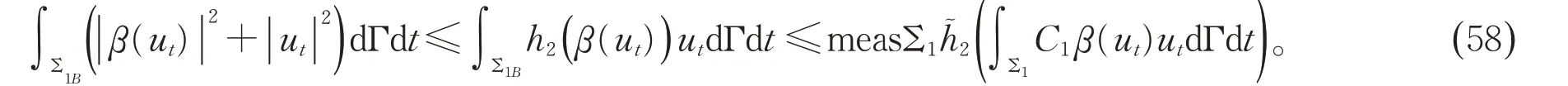
进一步,根据假设1 可得

类似于(58)的推导,由假设1 可得

则q(0)=0,q也是严格递增,显然,如果r>0,则q(r)>0。接下来类似文献[5,15]中的证明过程可推导出定理1 的结论,这里不再赘述。定理1 得证。
3 结论
本文通过使用乘子法研究了一类声学边界条件是非局部反应边界的波动系统的稳定性,获得了该类非线性系统在边界时滞扰动下的一般能量衰减率,将其归结为一个常微分方程的解。所获得的非线性时滞系统能量衰减率依赖于非线性耗散项的增长率。

