振动磨机环扇形激振板的横向振动与稳定性分析

杨勇强，张 曼

（陕西科技大学机电工程学院，陕西 西安 710021）

1 引言

振动磨机是一种矿产试样破碎加工的主要设备。振动磨机的原理是利用特殊研磨介质和矿料之间的相互碰撞、挤压和摩擦将矿料制成粉状。国内外学者对振动磨机进行了一定的研究。文献[1]采用有限元法进行了振动磨机的振动特性分析，得到了振动磨机整体的工作频率控制方法。文献[2]建立了离散磨介群动力学模型，计算获得研磨介质质点的速度、加速度以及应力应变的变化情况。文献[3]以振动强度和撞击力最大，研磨介质体积最小为优化目标，采用多目标遗传算法对立式振动磨机关键结构参数进行了多目标优化设计。上述研究主要针对振动磨机整机工作及研磨介质进行了分析，对其激振机构的研究较少。一种小型立式振动磨机，其核心部位为环扇形机构，如图1所示。该环扇形机构高速旋转产生激振力促使钵体产生振动，实现磨料工作。立式振动磨机的激振力、振动频率和振幅等参数与环扇形机构的结构和运动速度等因素有关[4]，环扇形激振机构的横向振动对振动磨机的整机运转产生较大影响，因此研究振动磨机环扇形机构的运动稳定性具有重要的理论意义。

近年来，许多学者对环扇形板横向振动问题进行了一定的研究分析。文献[4]利用有限元法分析了功能梯度扇形板的非线性自由振动问题。文献[5]在建立统一旋转结构动力学模型的基础上，分析了复杂边界条件下扇形板和类扇形板的自由振动问题。文献[6]在平面线弹性理论基础上，建立了环扇形板面内自由振动运动方程，并计算获得其自由振动的无量纲固有频率。以上动力学研究均未研究旋转角速度对环扇形板横向振动的影响，事实上，旋转角速度对其横向振动影响较大。基于此，本文以振动磨机的环扇形激振板为研究对象，对其在一定旋转角速度情况下的横向振动进行分析，并研究其运动稳定性问题。

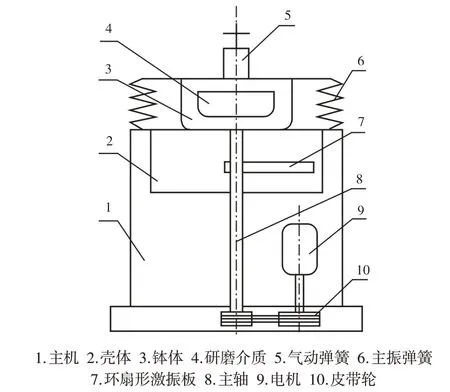
图1振动磨机示意图Fig.1 Sketch of Vibration Mill

2环扇形板运动微分方程的建立

该小型振动磨机的环扇形激振机构，如图2（a）所示。其结构可简化为环扇形板，如图2（b）所示。图中：h—环扇形板的板厚为，b—外半径，a—内半径，ϕ—扇形角，Ω—旋转角速度。

图2振动磨机环扇形激振板Fig.2 Annular Sector Excitation Plate of Vibration Mill

根据哈密顿原理，环扇形板横向振动运动微分方程为[7]：

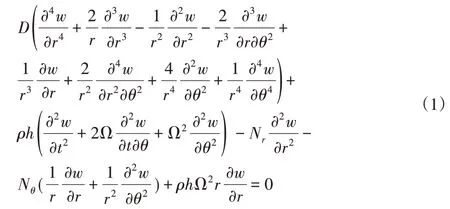
式中：w—横向挠度，抗弯刚度，E—弹性模量，μ—泊松比，N r和Nθ—环扇形板单位宽度的径向和环向拉压力，ρ—材料密度。

根据弹性小挠度薄板理论，利用平衡微分方程、物理方程和相容方程可得[8]：

式中：u r—环扇形板中面的径向位移；A和B—积分常数，与环扇形板的边界条件有关。外径边界条件为自由，即。根据边界条件计算A和B，得到环扇形板拉压力分别为：

3运动微分方程及边界条件无量纲化

引入下列无量纲量：

则方程（1）的无量纲形式为：

环扇形板拉压力无量纲化分别为：

设方程（6）的解为：

式中：ω—无量纲振动频率，j= -1。

将式代（9）入方程（6），得到环扇形板的运动微分方程为：

环扇形板内外径处的无量纲边界条件为：

4 微分求积法求解

利用微分求积法在环扇形板的径向和环向区域内取若干节点，则节点的横向振动函数值W及其各阶导数可用其函数值加权求和来表示。径向节点划分采用节点替代法（即δ法）进行非均匀划分，其计算公式为：

根据参考文献[9-10]，径向一阶导数权系数

径向高阶导数的权系数可以通过矩阵相乘求得，即：

环向节点划分及函数各阶导数B(kmj)权系数矩阵与上述径向情况类似，这里省略。采用微分求积法法离散化振动方程（10），其微分求积法形式为：

式（15）和（16）的微分求积形式联立得到的矩阵形式为：

其中，矩阵[R]，[G]和[K]中含有环扇形板的半径比、扇形角以及无量纲角速度等参数，式（17）构成了广义特征值问题。因此，振动磨机环扇形板的特征方程表达为：

5 无量纲复频率随无量纲角速度变化的数值计算与分析

根据磨料工况不同，该小型振动磨机环扇形板的半径比为ξ=0.25,0.305（内半径为55 mm，外半径为220mm，180mm），扇形角ϕ分别为π4和π2。以下对不同半径比和扇形角情况下的环扇形板无量纲复频率进行计算分析。

当半径比ξ=0.25，扇形角ϕ=π4时，旋转环扇形板前四阶模态无量纲复频率随无量纲角速度的变化情况，如图3所示。由图3可知，当无量纲角速度c=0，环扇形板自由振动的无量纲固有频率ω为实数。随着无量纲角速度c的增加，前四阶无量纲复频率Re(ω)实部为正值，虚部Im(ω)保持为零，表明板处于稳定状态。当c=0.72时，第1阶模态复频率实部Re()ω=0，而虚部Im()ω分为正负两个分支，说明环扇形板出现第1阶模态发散失稳。无量纲临界角速度c=0.72即为第1阶临界发散角速度。当c=0.96时，板又恢复稳定。当c=1.44时，第1阶和2阶模态发生颤振耦合；当c=0.90时，第3阶和4阶模态也发生颤振耦合。c=1.44和c=0.90分别为第1、2阶临界颤振角速度和第3、4阶临界颤振角速度。

图3 前四阶无量纲复频率随无量纲角速度变化曲线（ξ=0.25，ϕ=π4）Fig.3 First Four Order Dimensionless Complex Frequency Versus Dimensionless Angular Speed（ξ=0.25，ϕ=π 4）

当半径比ξ=0.305，扇形角ϕ=π4时，旋转环扇形板前四阶模态无量纲复频率随无量纲角速度的变化情况，如图4所示。由图4可知，当c=1.04时，环扇形板出现第1阶模态发散失稳，第1阶临界发散角速度c=1.04大于图3所示的第1阶临界发散角速度。当c=1.22时，板又恢复稳定状态。与ξ=0.25，ϕ=π4情况不同在于，环扇形板并没有发生第1阶和2阶颤振耦合失稳，仅仅出现了第3、4阶模态耦合失稳，相应的第3、4阶临界颤振角速度为c=0.48。

图4 前四阶无量纲复频率随无量纲角速度变化曲线（ξ=0.305，ϕ=π4）Fig.4 First Four Order Dimensionless Complex Frequency Versus Dimensionless Angular Speed（ξ=0.305，ϕ=π4）

当半径比ξ=0.25，0.305，扇形角ϕ=π4时，旋转环扇形板前三阶模态无量纲复频率随无量纲角速度的变化情况，如图5和6所示。由图5、图6可以看出，随着无量纲角速度c的增加，环扇形板均发生第1阶发散失稳现象以及第2阶和3阶颤振耦合现象。对比图5、图6，在半径比ξ=0.305，扇形角ϕ=π4情况下，当c=0.98时，旋转环扇形板第2和3阶模态的无量纲复频率实部Re(ω)分为两支，虚部Im(ω)为零，说明板在发生颤振耦合失稳之后又重新恢复稳定。同时，ξ=0.305情况下的第1阶临界发散角速度大于ξ=0.25情况下的第1阶临界发散角速度

图5 前三阶无量纲复频率随无量纲角速度变化曲线（ξ=0.25，ϕ=π2）Fig.5 First Three Order Dimensionless Complex Frequency Versus Dimensionless Angular Speed（ξ=0.25，ϕ=π 2）

图6 前三阶无量纲复频率随无量纲角速度变化曲线（ξ=0.305，ϕ=π2）Fig.6 First Three Order Dimensionless Complex Frequency Versus Dimensionless Angular Speed（ξ=0.305，ϕ=π2）

6 结论

采用微分求积法对振动磨机旋转环扇形激振板的横向振动和稳定性问题进行了分析，得到了旋转环扇形板的前三（或四）阶复频率的实部和虚部随旋转角速度的变化情况。分析结果表明，随着无量纲角速度的增加，振动磨机环扇形板发生第1阶模态发散失稳现象和其它阶模态的颤振耦合失稳现象，颤振耦合失稳现象发生的模态阶数与环扇形板的半径比和扇形角有关。上述结果为振动磨机激振系统的设计与研究提供了一定的参考依据。