改进Zernike矩的运动靶标高精度定位算法
朱帅飞,马 伟,杨 芳
(1.河南科技大学机电工程学院,河南 洛阳 471003;2.河南省机械设计及传动系统重点实验室,河南 洛阳 471003)
1 引言
图像的边缘检测是运动目标中心定位中的重要一环,直接影响着运动目标中心位置检测的精度。传统的边缘检测方法包括Sobel、Roberts、Canny、Prewitt、Laplacian等,但是这些方法在硬件设备一定的情况下,检测精度只能达到像素级。随着对检测精度的要求的提高,传统的检测方法早已不能满足我们的需求,很多学者把目光转向了亚像素边缘检测领域,而且取得较大的进展[1]。
在亚像素边缘检测算法中,基于Zernike矩的亚像素边缘检测算法由于其独特的优点促使国内外学者对其进行了大量的研究。文献[2]建立了理想的灰度模型,利用Zernike矩的旋转不变形,通过3个不同阶次的Zernike矩来计算定位所需要的4个参数,最终实现了亚像素级别的边缘定位。文献[3]为了提高Zernike矩边缘检测的速度,在传统算法的基础上将傅里叶变换函数与Zernike矩相结合提出了一种新的检测算法,并通过一系列的实验对检测速度进行了验证;但是该算法边缘检测的精度不高。文献[4]通过对三角函数的分析,结合三角函数的对称性和反对称性的特点,对原有的Zernike矩进行了改进,在一定程度上提高了算法的检测精度。文献[5]针对Zernike矩边缘检测的图像存在的边缘较粗、精度不高等问题,从边缘判据和卷积模板的大小两个方面出发,对其进行改进,从而达到了提高边缘检测精度的目的。文献[6]将小波能量熵与二维Zernike矩相结合,来进一步改善图像边缘检测的精度,并且将该算法推广到工程实践中实现了对IC芯片表面的定位识别。文献[7]等对传统的形态学梯度算子进行了改进,利用改进后的梯度算子作为边缘粗定位,再通过Zernike矩算法对图像进行重定位,通过这两种结合的方式提高了算法的精度和抗噪性。
以运动靶标中心定位为研究对象,提出了一种基于改进Zernike矩的亚像素边缘定位算法。该算法首先采用改进的Can⁃ny边缘检测算法对图像进行粗定位,再采用提出的改进的Zernike矩算法对图像进行亚像素级重定位,并且对误差进行了分析和补偿,然后利用最小二乘法拟合确定靶标的中心,最终通过坐标变换实现了靶标位置的空间定位。
2靶标标记圆像素级边缘粗提取
2.1改进的Canny边缘检测算法
经典的的Canny边缘检测算法利用高斯滤波降噪,会造成图像边缘模糊,影响之后的亚像素定位。自适应中值滤波不但可以有效的滤除噪声,而且可以能够较好的保留图像边缘的完整度和图像的细节[8]。利用自适应中值滤波代替经典的的Canny边缘检测算法中的高斯滤波。自适应中值滤波算法主要分为如下两个步骤:
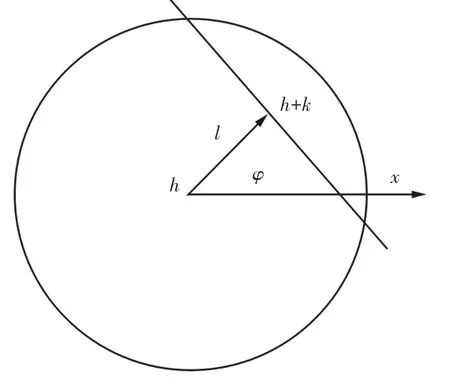
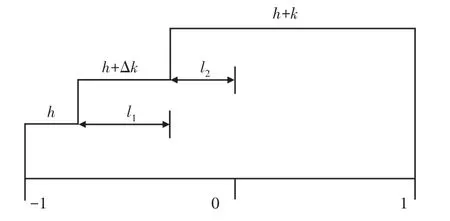
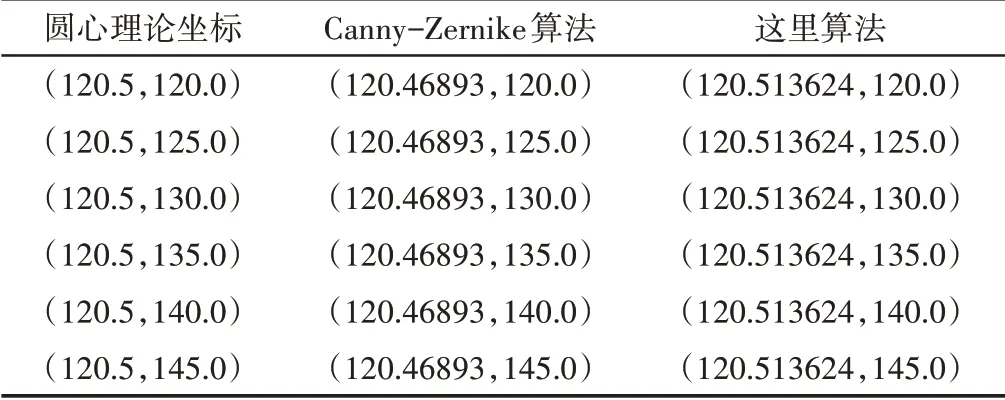
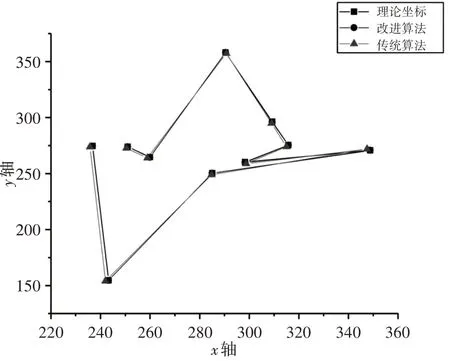
(1)若fmin (2)若fmin 可以看出,算法中噪声的检测和认定时以fmin和fmin为基准的,如果fmin 其中,f ij表示点(i,j)的灰度值,s i j为当前工作窗口。fmin表示当前工作窗口s ij中灰度的最小值;fmax表示当前工作窗口s ij中灰度的最大值;f med表示当前工作窗口s ij中灰度的中值;smax预设允许的最大窗口。 图像在平移或旋转时,圆形中心定位精度影响较小,算法的稳定性较好;而对矩形中心定位精度影响很大,算法的稳定性差[9]。因此在运动靶标上制作圆形标记,标记圆的中心点作为特征点。靶标标记圆像素级边缘提取步骤如下: (1)对采集到的靶标图像进行预处理。 (2)将R G B转化为HSV模型,通过颜色特征作为提取的标准,提取出感兴趣的区域即靶标标记圆,最后采用改进的边缘检测算法,对提取出的标记圆进行像素级边缘提取。 其中原始图像和像素级提取后的图像,如图1、图2所示。 图1原始图像Fig.1 The Original Image 图2提取后图像Fig.2 The Extracted Image 一副图像中p阶q次Zernike矩定义如下: 当图像为离散形式时,其理论公式如下: Zernike正交矩的很重要的一个特性是拥有旋转不变的性质,根据这个特性可知当转角为φ时,旋转前的正交矩A pq和旋转后的正交矩关系如下:根据这个特性,可以推导得到其它所需要的参数,从而实现图像边缘的亚像素定位。 传统的Zenike正交矩在计算时,灰度边缘模型采用的是理想的二级阶跃边缘模型,如图3所示。其中参数k表示阶跃高度,参数h表示背景灰度,l表示圆心与理论边缘之间的垂直长度,φ表示l与坐标轴x轴之间的夹角。 图3 二级理想灰度模型Fig.3 Two-Level Ideal Gray Model 式中:f′(x,y)—旋转后的边缘函数。 由上式进一步可得旋转角度为: 进而推导出模型的多元方程式如下: 由此可以推导出模型中各参数l,k,h的表达式,如式(9)所示。 最终得到图像亚像素边缘点的位置坐标如下: 经典的Zernike边缘检测算法中亚像素边缘判据为k≥τ⋂l≤δ,其中δ为1 2,由上面可以推导得出φ,h,l,k四个参数。其中阈值τ的选取的自由的,其值影响着亚像素边缘检测的效果。若阈值τ选取太小,亚像素边缘检测结果中会出现较多的虚假边缘;若阈值τ选取太大,则会导致亚像素边缘检测时丢失较多的边缘信息。传统的阈值τ选取是经过人工手动选取的,通过多次反复调整阈值τ使亚像素边缘检测达到理想的效果,不仅降低了检测效率而且精测的精度会随着调试人员的情绪问题而变得不稳定,无法保证其检测质量。 基于迭代法的最佳阈值选取是采用逼近的思想,其原理是先选取一个估计值作为阈值,然后利用此阈值对图像进行分割,根据生成的子图像的特征来选取新的阈值,再采用新的阈值来分割图像,经过一定次数的循环,使图像中错误分割的像素点达到最少。 图像中相同像素点的灰度值与阶跃灰度值在其像素点及其邻域内的变化趋势相同,因此可以利用迭代法求最佳阈值的方法求出最佳阶跃灰度阈值τ。具体步骤如下: (1)初始值的选取 式中:Zmin、Zmax—图像中最小阶跃灰度值和最大阶跃灰度值。 (2)根据阈值T k将图像分为两部分,并分别求出两部分的平均阶跃灰度值。 式中:Z(i,j)—图像上(i,j)点的阶跃灰值;N(i,j)—(i,j)点的权重系数。 (3)求解新阈值 (4)如果T k=T k+1,即阶跃灰度最佳阈值τ=T k=T k+1迭代结束,反之k=k+1转向步骤(2)。 改进的Zernike边缘定位算法检测流程,如图4所示。其大致可以分为以下几个步骤: 图4 改进算法检测流程图Fig.4 Flow Chart of Improved Algorithm Detection (1)采用传统的Zernike矩检测算法分别求得三个不同阶次的Zernike矩A00,A11,A20,φ; (2)根据Zernike正交矩旋转不变的性质,计算得到A′00,A′11,A′20; (3)将阶跃灰度值作为研究对象,利用4.1基于迭代法求取阶跃灰度最佳阈值τ; (4)根据亚像素边缘判据为k≥τ⋂l≤δ,对图像中像素点进行判别。符合条件k≥τ⋂l≤δ,则该像素点为边缘像素点,反之不成立。 在选取卷积模板时,由于模板大小的不同会引起误差。若模板大小为N×N,其覆盖区域是模板中心周围N2个像素,在单位圆内取样时,此时单位圆半径变成N∕2,则需要把计算出来的垂直距离增大两倍,补偿后的亚像素边缘检测坐标公式如下: 上述亚像素边缘检测位置坐标的推导是基于理想的二级阶跃边缘模型,即一个表示背景灰度另一个表示前景灰度。但是图像中图形的边缘是以灰度渐变的形式存在的,实际的边缘模型更接近三级阶跃边缘模型,即一个表示背景灰度,一个表示目标灰度,另一个表示过渡阶段灰度,其模型,如图5所示。 图5 三级灰度模型示意图Fig.5 Three-Level Ideal Gray Model 类似于传统的Zernike矩亚像素边缘检测位置坐标推导方法,同理可以得到如下的公式: 将传统的Zernike边缘检测算法计算得到的l与三级灰度模型得到的l m做差,可推导偏差e如下: 当图像边缘位于模板中心的两侧像素及其邻域时,则可以利用偏差e对传统的Zernike边缘检测算法计算得到的l进行补偿,从而达到提高亚像素边缘精测的精度的目的。 利用上述改进的Zernike矩算法可以得到靶标标记圆的一系列亚像素边缘点,然后通过最小二乘法可以拟合得到标记圆的圆心图像坐标位置,随后采用文献[10]的方法对摄像机进行进行标定,根据得到的标定参数通过坐标变换最终得到靶标的空间位置。其中最小二乘法理论公式如下: 式中:p(x i,y i)—离散的亚像素边缘点;N—离散的数;(x0,y0)—目标的坐标位置;r—圆半径。 第一组实验是计算机仿真实验,为了对两种算法的检测精度进行检测,制做了一副分辨率为(256×256)的图像。以一系列点为圆心坐标,圆半径为60像素,图像背景像素值为0,如图6所示。分别采用传统的Zernike算法与改进算法对圆心坐标进行定位,然后利用最小二乘法拟合得圆心图像坐标位置,如表1所示。通过表1可知传统算法的定位误差为0.03107像素;改进算法定位误差为0.013624像素,表明算法检测精度优于传统Zernike算法。 图6 仿真所用图像Fig.6 The Image for Simulation 表1 仿真结果Tab.1 Simulation Result 第二组实验:在省基金的支持下我们搭建了柔索驱动机构实验平台。实验台主要包括机械结构和电气控制系统,机械结构部分主要由机架、靶标的运动平台、柔索、靶标等模块组成;控制系统主要由用户操作界面、图像采集卡、运动控制中心、伺服电机、驱动器等模块构成,实验台,如图7所示。 图7 柔索驱动机构实验平台Fig.7 Experimental Platform for Cable Driving Mechanism 其中采集装置为德国巴斯勒acA2000-340kc型号的工业相机,分别率为2046*1086,编程平台为vs2013,编程语为c++结合OpenCV2.4.10。在驱动靶标运动的过程中,首先分别采用传统的Zernike算法与这里改进算法分别对运动靶标中心进行亚像素边缘提取,然后采用最小二乘法对提取的亚像素边缘进行拟合,最终通过坐标变换得到靶标中心空间坐标。通过进行对比分析,来验证改进算法的检测精度。在靶标运动过程中抽取十个数据点,将计算坐标与理论坐标进行了对比分析,实验结果,如表2所示。 表2 实验结果Tab.2 SimulationResult 三条曲线比较接近,不容易直观地对其进行区分、评价,如图8所示。为了对两种算法的检测精度进行定量的分析,将这些实验数据进行了整理分析,整理后的数据,如表2所示。通过表2可知传统Zernike算法的x方向最大误差为1.269mm,平均误差为0.787mm,y方向最大误差为1.451mm,平均误差为1.065mm;改进算法x方向最大误差为0.744mm,平均误差为0.475mm,y方向最大误差为0.819mm,平均误差为0.65mm。显然,改进算法的检测精度要优于传统的Zernike算法;同时最佳阈值的自动选取相比于相比于人工手动调试具有更高的效率,为后期柔索机构伺服反馈、高精度的控制提供了有效依据。 图8 算法对比曲线Fig.8 Algorithmic Contrast Curve 经典的Zernike矩算法边缘检测判据中因为自由阈值的存在,降低了检测效率,且传统的检测方法对误差的来源未进行分析,也未考虑误差补偿,造成检测精度的下降。针对这两个检测的难题,提出一种基于改进Zernike矩的亚像素边缘定位算法。以运动靶标中心定位为实验研究对象,测试结果表明:该方法能够准确对运动靶标中心进行定位,检测精度要优于传统的Zernike算法,同时最佳阈值的自动选取相比于人工手动调试具有更高的效率。2.2像素级边缘粗提取


3传统的Zernike边缘定位算法
3.1图像中Zernike矩定义



3.2 Zernike亚像素边缘定位原理



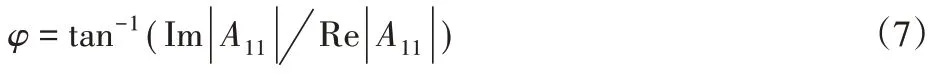

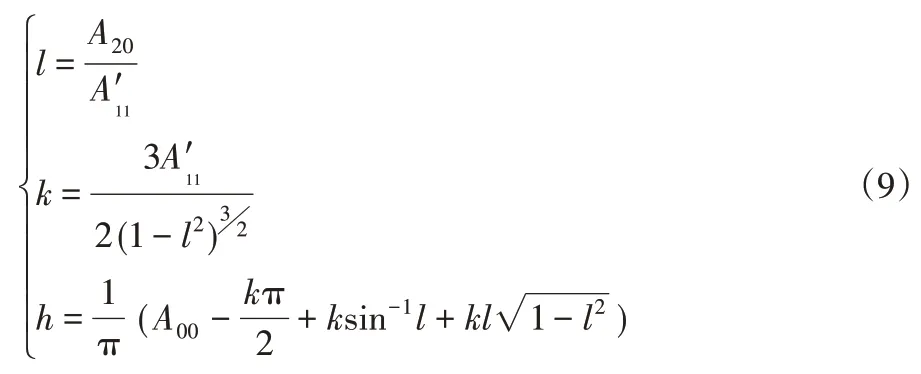

4 改进的Zernike边缘定位算法
4.1 基于迭代法的阶跃灰度最佳阈值选取



4.2 改进的Zernike边缘定位算法检测流程

5 误差分析及补偿
5.1 卷积模板引起的误差

5.2 边缘模型选取引起的误差

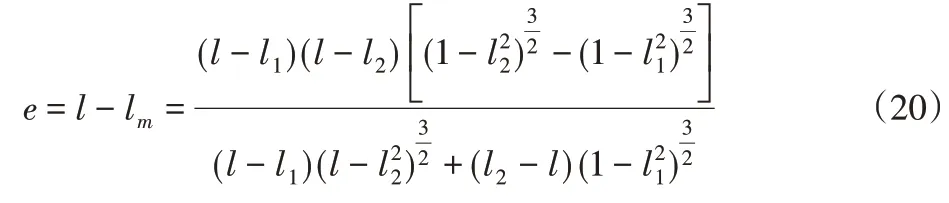
6 最小二乘法拟合靶标圆心坐标

7 实验结果及分析



8 结论

