螺旋给料机结构优化设计
王友胜,许焕敏,高 腾,甘润节
(河海大学机电工程学院,江苏 常州 213022)
1 引言
作为一种有连续进给能力和较高进给精度,同时兼备混合、搅拌、称重等功用的无挠性牵引设备[1],螺旋给料机由于其结构简单、对环境污染小、使用较为便捷,经常在化工、粮食加工等领域被用于输送流动性较好、无粘性或者粘性较小的粉体物料以及相应磨琢性较小的颗粒物料[2-3],某公司螺旋给料机实物图,如图1(a)所示。工作中,由于物料属性、工作环境不同,有可能会出现卡料、堵塞现象,进而导致给料机输送量、进给效率较低。为此,就得到适应性较强、进给效率较高的机型,国内外学者开展了大量的研究。
文献[4]通过分析大倾角输送机中单个颗粒运动特性,通过理论与实验结合的方式,准确预测了实际生产率;文献[5]利用DEM对颗粒在螺旋体内的运动进行数值模拟分析;文献[6]通过将多个三维输送机模型导入EDEM中,定量地分析了螺旋转速、螺距大小等因素对给料过程的影响;文献[7]以提高输送效率为优化目标,建立优化模型并结合蚁群算法得到最佳优化参数;文献[8]从螺旋给料装置和螺旋给料仿真两方面着手,详细分析了国内外关于螺旋给料装置的研究现状,指出了理论仿真模型与真实结构之间仍存在一定偏差;文献[9]利用离散元方法研究了螺旋体参数的变化对输送量以及功率消耗的影响,为螺旋体设计提供了理论支持;文献[10]对螺旋输送机的输送性能进行了大量的实验研究。以上研究都主要是螺旋给料机的主要参数设计和输送过程分析,没有对优化后的螺旋体结构进行相应的有限元分析,无法得知新结构是否满足实际要求。
螺旋体是螺旋给料机的核心组件,直接影响着整机的输送性能,螺旋体结构实体,如图1(b)所示。螺旋体中所涉及的参数较多并且相互之间存在影响,因此很难用传统的设计方法得到最优结果。本课题在以先建立起各参数数学模型基础上,确定合理的优化目标;然后在Matlab中编写相应的M文件,求解得到优化结果。根据相应的优化结果参数,在Inventor中建立螺旋体三维模型,再将其转换成igs格式;导入ANSYS中进行有限元分析,对三维模型结构强度进行验证。

图1螺旋给料机实物展示Fig.1 Physical Display of Spiral Feeder
2给料机原理与螺旋体模型
2.1给料机工作原理
作为螺旋输送装置,螺旋给料机工作原理跟输送机类似,都是在进料口处,将物料投入壳体内,同时螺旋体即螺旋叶片与转轴在电机的驱动下做高速旋转运动;投入壳体的物料受到螺旋叶片的推力作用使得其沿轴向运动,因自身重力的影响,物料在向前推进过程中又会自动坠落,故而物料在壳体内的运动轨迹为复杂的空间曲线运动[11]。
2.2螺旋体模型
即为图1(b)所示该型号螺旋体参数模型,如图2所示。包括螺旋叶片与螺杆轴两部分;其主要参数有:叶片直径D,螺距S,螺旋杆外径d,螺旋杆内径d0,叶片厚度t,螺杆长度L,叶片高度h。本课题以该产品为实例进行优化设计,已知螺旋叶片的材料为Q235A,螺旋杆的材料为45钢,相关参数如叶片厚度t=3mm,叶片高度h=7mm,螺杆长度L=1.1m,当前输送量可达到20t∕h。

图2螺旋体参数模型Fig.2 Spiral Parameter Model Diagram
3螺旋体参数优化模型
3.1参数设计变量
考虑到产品参数标准化的重要性以及螺旋体实现规模化生产,相关螺旋体尺寸如,叶片厚度t以及高度h、螺杆长度L都是固定的,尺寸大小如2.2中所述;需优化的参数则包括螺旋叶片直径D,螺距S,螺杆外径d、内径d0,变量表达式,如式(1)所示。
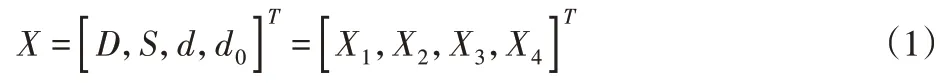
设计螺旋体时,需要选择合理的尺寸大小,同时参数优化的过程,即是在满足给定条件前提下,在一定范围内求出变量的最优值。查阅资料,相关尺寸叶片直径D取值范围是(0.15,0.35),螺距S是(0.1,0.5),螺杆外径d是(0.05,0.15),螺杆内径d0是(0.03,0.05),尺寸单位均为米(m)。
3.2目标函数
对螺旋体结构进行优化,主要就是在以满足结构的刚度和硬度为前提,降低螺旋体的质量,一方面可以达到节约降本的目的,同时优化后的螺旋体进给的效率更高。螺旋主体的总重量有螺旋叶片和螺杆组成,所以建立的螺旋体质量参数模型包括叶片质量模型和螺杆质量模型,相对应的目标函数如下:

式中:G—螺旋体重量(kg);V1—螺旋叶片体积;V2—螺杆轴体积;

将V1、V2代入上式,其中L、t、ρ1均为常数,则目标函数表达,如式(3)所示。

3.3设计约束条件
(1)合理的叶片螺距有助于避免出现给料过程卡塞现象,相应约束条件,如式(4)所示。

(2)给料机进给效率不小于最小值,相应约束条件,如式(5)所示。

式中:αx—螺旋半径为x处的螺旋升角;ρ2—粉体物料与叶片之间的当量摩擦角
(3)刚度限制条件
对螺杆轴进行力学分析时,可将力学模型简化成简支梁,螺杆轴最大挠度不应大于许用值,相应约束条件,如式(6)所示。


(4)功率限制条件
螺旋给料机在工作中的功率应不应大于电机的额定功率,即P负≤P额,相应约束条件,如式(7)所示。

式中:P额—电机额定功率,取3kW;K—电机使用安全系数,取K=1.2;μ1—粉体物料与机槽间摩擦系数,取μ1=0.4;H1—物料在进料口的有效堆积高度,取H1=0.25m;L1—进料口长度,L1=0.28m;R—料槽截面半径,取R=(0.5D+0.01)m。(5)转速限制条件
螺旋轴的转速在满足输送能力的条件下不宜过高,以免物料受过大的切向力而被抛起进而影响输送效率,故螺旋转速n不能超过极限转速nmax,如式(8)所示。

式中:n—螺旋轴转速(r∕min);A—输送粉体时物料综合系数,A取75。
(6)扭转强度限制
由于螺旋给料机螺旋轴是空心轴,故而空心轴的最大剪切力τmax应不大于许用剪切力,取许用剪切应力相应约束条件,如式(9)所示。

式中:T—螺旋轴扭矩;Wn—抗扭矩截面系数。
4 算法优化求解及有限元分析
4.1 遗传算法
遗传算法是以自然界中物竞天择、适者生存为依据,模拟生物进化历程中优胜劣汰和染色体信息相互交换、结合的高效寻优算法。其可在限定的搜索空间内,用区别于传统搜索算法的方式,不断地进行寻优,直至最优解。
本课题基于经典遗传算法,首先在Matlab中建立螺旋体质量相关数学模型、变量约束条件等遗传准备工作,然后计算每个关于质量的解在种群中的适应度值,再通过选择、交叉、变异遗传操作,得到最优解即最佳螺旋参数值,具体求解过程,如图3所示。

图3 算法求解过程Fig.3 Soluting Process of Genetic Algorithm
在Mtalab中编译关于螺旋体质量寻优的程序代码,选定初始种群大小为20,最大遗传代数为50,个体长度为10,交叉概率为0.7,变异率0.02,相应部分程序如下,程序运行得到遗传进化代数图,如图4所示。



图4 遗传进化代数Fig.4 Genetic Evolution Algebra
4.2 优化结果及有限元分析
在Matlab中编制基于遗传算法优化目标的M文件,运算求得关于螺旋叶片直径、螺距等螺旋体参数最优值,具体数值,如表1所示。

表1 优化前后参数比较Tab.1 Comparison of Parameters before and after Optimization
由表中的优化结果可知,优化后的螺旋叶片直径较之前减小20mm,螺距增加25mm,螺杆轴外径大小增加4mm,螺杆内径减小2mm,螺旋升角提高4°,螺旋进给效率提高8.2%,螺旋体重量减轻1.4kg;由相关数据表明螺旋体优化的目标包括质量得到减轻,效率得到提升,满足预期要求。
基于优化后的参数结果,建立新三维实体模型,将优化前后的螺旋体结构模型分别在ANSYS环境下进行有限元分析。划分单元网格大小为1mm,生成247007个节点,包含131449个单元;优化前、后的螺旋体应力分布情况,如图5(a)、图5(b)所示。

图5 优化前后等效应力分析Fig.5 Equivalent Stress Analysis of Pre-Optimal and after
根据等效应力分析结果表明,优化前的螺旋体最大等效应力结果为220.626MPa,优化后的螺旋体最大等效应力为183.87MPa,通过此次优化设计,螺旋体的最大等效应力降低36.756MPa;通过优化前后对比,螺旋体的强度得到提升,增强了其工作中的可靠性。
5 结论
针对提高螺旋给料机工作适应性、进给效率和螺旋体轻化,提出了一种基于遗传算法的螺旋体参数优化设计,并模拟实际工况对优化后的机体模型进行有限元分析。通过优化计算和仿真分析,得到以下结论:在满足使用要求和工作强度等限制条件下,该方法使得螺旋体质量减轻9.34%,进给效率提高8.2%,仿真分析结果显示最大等效应力降低16.7%;此方法合理地优化了给料机的设计参数,增强了给料机适用性,减轻螺旋体重量和提高输送效率,同时也提高了其工作强度,进而节省了资源,提高了经济效益。

