改进的超短基线系统自适应相位差估计器
喻敏,丁贤君,张晓亮,祝明思
(1.武汉理工大学 交通学院, 湖北 武汉 430070;2.中国船舶工业系统工程研究院,北京 100036)
0 引言
超短基线定位系统通过测量相位差来估计目标方位,准确估计基元间接收信号的相位差是超短基线定位系统的关键技术之一。由于海洋信道是复杂的、多途的随机时变空变信道,自适应滤波器比固定参数滤波器具有更好的处理性能,使得自适应Notch滤波器(ANF)成为估计窄带相位差的经典方法。
截至目前,已有大量学者研究了ANF在相位差估计中的应用。文献[1]提出了设计极窄带ANF的方法,介绍了将其用作相位估计器的概念,该估计器的优势是能同时完成信号检测和相位差估计。文献[2]进一步提出了利用ANF来估计单频矩形脉冲(CW)信号的瞬时频率、信号包络和瞬时相位。针对频率未知或者存在频差的情况,文献[3]提出频点自跟踪自适应估计器,文献[4]提出基于极坐标系、以幅值和相位为正交基的相位估计方法。为了研究ANF在多目标定位中的应用,文献[5]给出了多路并联ANF的结构,文献[6-7]进一步分析了单通道、并行多通道和串行多通道3种滤波器的工作特性。
相位差估计器中应用最广泛的自适应算法是最小均方(LMS)算法,它具有结构简单、计算量小和易于硬件实现的优点。但是其步长因子μ是固定的,稳态精度与收敛速度、自适应跟踪能力不可兼得。针对传统LMS算法存在的固有矛盾,研究者们对步长μ提出了一系列改进算法。文献[8]将瞬时误差引入μ的更新过程,在迭代初期,为了加快收敛速度,μ的取值较大,但同时也增加了稳态失调。文献[9]将瞬时误差的Sigmoid函数作为μ的更新准则,可以同时提高收敛速度、稳态精度和跟踪能力,但当瞬时误差趋于0时步长变化太大,易出现稳态失调。此外,双曲正弦函数[10]、双曲正切函数[11]、对数函数[12]、指数函数[13]和箕舌函数[14]等函数也被作为μ的更新准则。其中,基于双曲正切函数变步长LMS(tanh-LMS)算法的收敛速度优于Sigmoid函数,具有较好的综合性能,但其步长受误差函数的影响较大,导致稳态失调较大。另外一种应用较为广泛的自适应算法是最小二乘(RLS)算法,但尚未在自适应相位差估计器中得到广泛应用,文献[15]仅将RLS算法作为滤波预处理,以提高广义互相关时延估计精度。
本文针对tanh-LMS算法稳健性的不足,基于噪声和信号的相干性提出改进的tanh-LMS算法,以增强自适应算法的抗干扰能力。同时,为避免LMS算法步长选择,将RLS算法应用到自适应相位差估计器中,以降低估计器的稳态误差。进而通过数值仿真分析LMS算法和RLS算法两种自适应相位差估计器的参数取值问题,最后利用实验数据对两种估计器的收敛性能进行对比验证。
1 自适应相位差估计器
在超短基线定位系统的应用中,信号频率已知,采用基于LMS算法的两个正交权的ANF可实现信号相位估计。将两路ANF并联,即可得到自适应相位差估计器,其结构如图1所示。图1中,rs(t)和rc(t)为两路正交的参考信号,xi(t)(i=1,2)为输入信号,yi(t)为输入信号,si(t)为输入声源信号,ni(t)为背景噪声,ωsi和ωci分别为rs(t)和rc(t)的权向量,εi(t)为残差,代表不同线路的自适应Notch滤波器。

图1 自适应相位差估计器
对于第1路ANF,s1(t)=B1cos(ω0t-φ0),B1为第1路输入声源信号幅值,ω0为信号频率,t为时间序列,φ0为初始相位。则rs(t)和rc(t)分别为
(1)
式中:A1为第1路参考信号的幅值。利用LMS算法可对两个权向量ωs1和ωc1进行自适应学习。将其过程离散化为
(2)
当ANF稳态收敛时,可得滤波器最佳稳态权为
(3)
由此得到相位值
(4)
同理,利用第2路ANF估计输入声源s2(t)的相位为
(5)
两路信号之间的相位差[1]可表示为
(6)
式中:k为采样点序号,k=1,2,…,n,n为采样点个数。
2 改进的LMS自适应算法
2.1 改进LMS算法的原理
LMS算法中步长的取值是影响整个算法收敛性能的关键参数之一。文献[11]提出的变步长tanh-LMS自适应算法,在低信噪比时,该算法收敛性、跟踪性、稳态性均优于其他多种变步长算法,但该算法存在步长μ受误差函数ε(n)影响较大的问题。为此,本文将tanh-LMS自适应算法中μ值的更新过程改进为
(7)
式中:μ0为初始步长;参数a控制双曲正切函数的幅度;参数b和c控制函数的形状,决定曲线上升的速度。在起始迭代阶段,要有较大的μ值,以保证较快的收敛速度和跟踪速度;在达到收敛状态后,μ值保持较小的值,以减少稳态失调。为了分析改进tanh-LMS算法的性能,定义权系数的偏差矢量为
Δω(n)=ωo-ω(n),
(8)
式中:ωo为最佳权系数。则有第n次迭代的期望信号为
(9)
式中:ζ(n)为零均值白噪声,且与输入信号x(n)相互独立。根据LMS算法,d(n)可表示为
d(n)=ε(n)+ωT(n)x(n),
(10)
式中:ε(n)第n次迭代的滤波器误差。(8)式和(9)式代入(10)式,可得
ε(n)=ΔωT(n)x(n)+ζ(n).
(11)
由(11)式可得
E[ε2(n)]=E[ΔωT(n)x(n)xT(n)Δω(n)]+
E[ΔωT(n)x(n)ζ(n)]+
E[ΔωT(n)x(n)xT(n)Δω(n)]+E[ζ2(n)]=
E[ΔωT(n)x(n)xT(n)Δω(n)]+E[ζ2(n)],
(12)
E[ε(n)ε(n-1)]=
E[ΔωT(n)x(n)xT(n-1)Δω(n-1)]+
2E[ΔωT(n)x(n)xT(n)ζ(n-1)]+
E[ζ(n)ζ(n-1)]=
E[ΔωT(n)x(n)xT(n-1)Δω(n-1)].
(13)
文献[11]提出的变步长tanh-LMS自适应算法使用ε2(n)来调整步长,而本文采用ε(n)ε(n-1)来调整步长。通过比较(12)式和(13)式可以发现,E[ε2(n)]受到背景噪声ζ2(n)的影响,而E[ε(n)·ε(n-1)]不受ζ2(n)的影响,背景噪声对步长μ的影响较小。因此,本文提出的改进算法利用噪声与输入信号间的相关性,进一步提高了LMS算法的抗干扰能力。
2.2 参数对改进LMS算法的影响
下面通过仿真计算,对参数a、b和c的取值进行分析。仿真条件设置为:SNR=20 dB,权向量初始值为0,后续仿真中均沿用上述仿真条件。步长初始值μ0=0.004,单次仿真只改变一个参数,相位差估计的均方误差如图2~图4所示。

图2 a值对改进tanh-LMS算法相位差估计器收敛特性的影响(b=2.5,c=0.05)

图3 b值对改进tanh-LMS算法相位差估计器收敛特性的影响(a=2.5,c=0.05)
从图2~图4中可以看出:a值对μ的起始迭代速度影响较小,当迭代次数增加时,a值越大,估计器收敛的速度越快,但稳态后的均方误差增加;b值对稳态精度的影响较大,b值越大,稳态误差越大;c值越小,估计器的收敛时间越长。综合考虑,并经过大量仿真研究,认为较合适的估计器参数取值为a=2,b=0.5,c=0.005.
如图5所示,对基于传统LMS算法、tanh-LMS算法和改进tanh-LMS算法的3种自适应相位差估计器性能进行数值仿真。其中,传统LMS算法的步长μ=0.02;tanh-LMS算法的参数取值为:α=2.5,β=0.005[11].由图5可知,与传统LMS算法估计器和tanh-LMS算法估计器相比,改进tanh-LMS算法相位差估计器的收敛速度更快,而且稳态误差更小。
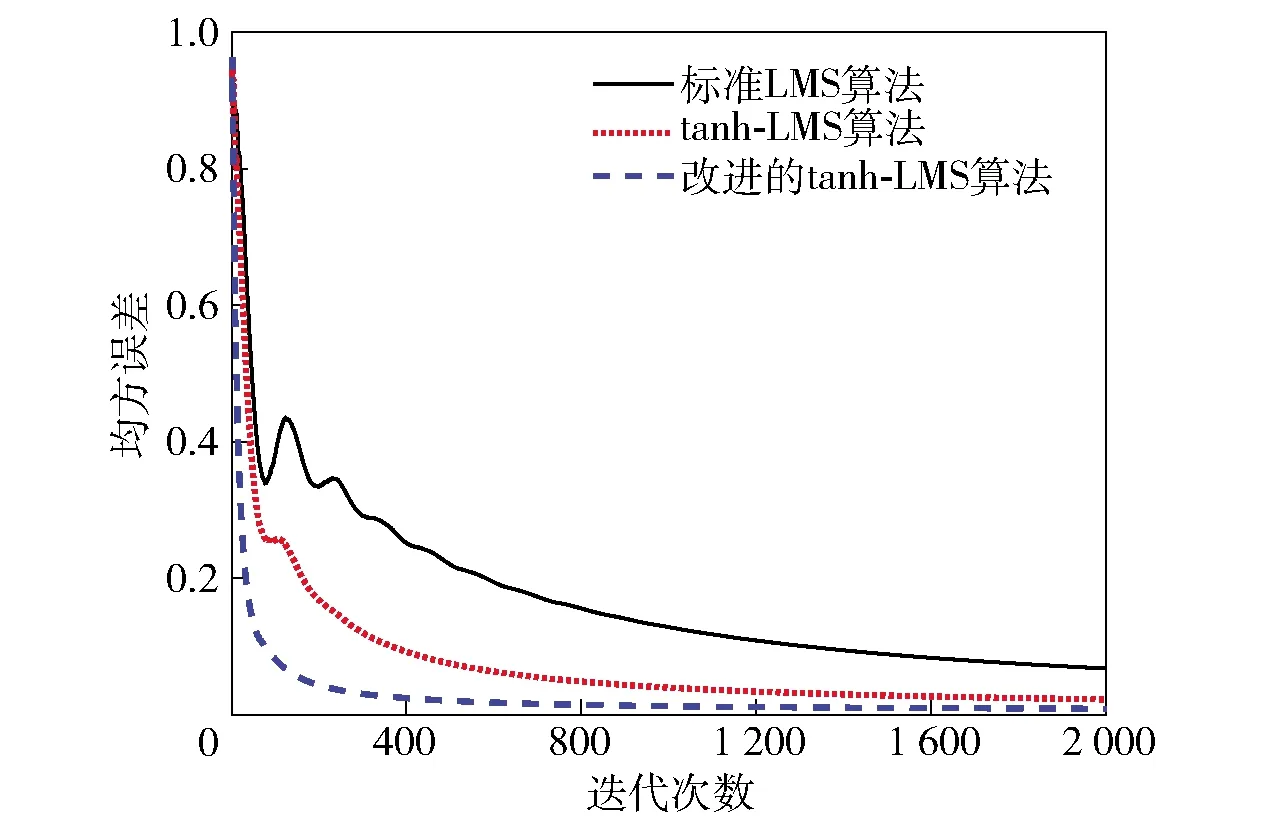
图5 3种算法相位差估计器收敛特性的对比
3 RLS算法自适应相位差估计器
除了LMS算法,RLS算法本身就具有更快的收敛速度,也可以应用到自适应相位估计器中。
基于RLS算法的自适应相位差估计器的代价函数可以表示为
(14)
式中:ξ(n)为估计误差和;λ为遗忘因子;en为估计误差。通常,赋予更新的采样点的估计误差更多的权重。
滤波器的抽头权系数可以通过最小化公式(14)式中的ξ(n)来更新:
餐厅名称,也是别有学问的。“局气”,北京话,“气”字读轻音,指公平、公正、守规矩、讲道理,也有仗义,大方,豪爽之意。
(15)
式中:
Ψλ(n)=λΨλ(n-1)+r(n)rT(n),
(16)
r(n)为输入信号的自相关矩阵;
θλ(n)=λθλ(n-1)+r(n)x(n).
(17)
为了计算矩阵Ψλ(n)的逆,根据矩阵求逆引理,得到Ψλ(n)逆矩阵的递推形式为
(18)
为了简化,定义增益向量为
(19)
(20)
重新整理(20)式,增益矩阵k(n)也可以简化为
(21)
(n)=(n-1)+k(n)n-1(n),
(22)
在第n次迭代中,抽头权系数的改变量取决于先验估计误差n-1和增益向量k(n)的内积。增益矩阵的作用类似于传统估计器中的步长参数,由于增益矩阵可以根据各个时刻的采样数据实时更新,使得基于RLS算法的自适应相位差估计器具有更充分利用新信息的能力。
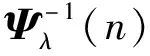

图6 RLS算法相位差估计器收敛特性
从图6中可以看出,与传统LMS算法估计器相比,RLS算法估计器估计精度较高,抗噪能力强,具有较好的收敛性能和稳定性。对RLS算法而言,λ值取值越小,收敛时间越短,但收敛后的噪声也偏大。考虑到λ值越趋近于1,估计器具有更长的有效记忆长度,稳态误差更小。因此,认为λ取0.95较为合适。
4 数值仿真
下面通过数值仿真对两种估计器的收敛速度、稳态误差和跟踪能力进行对比。
改进tanh-LMS算法自适应相位差估计器的参数取值为:a=2,b=0.5,c=0.005,步长初始值μ0=0.004.RLS算法的遗忘因子λ=0.95.权向量初始值均取为0.仿真条件同上,两种相位差估计器的均方误差曲线如图7所示。

图7 两种自适应相位差估计器的收敛特性
由图7可知,改进tanh-LMS算法自适应相位差估计器的收敛时间更短,而RLS算法估计器的稳态误差更小,二者总体性能接近。
由于水声信道复杂且多变性,系统接收到的信号可能会发生突变。针对信号突变的现象,仿真比较两种自适应相位差估计器的跟踪性能,并与传统的LMS算法进行对比。接收信号为CW窄带信号,在第500次采样点处设置幅值和相位突变。仿真结果如图8所示。

图8 3种自适应相位差估计器的跟踪曲线
由图8可知,针对信号突变,本文提出的两种方法对信号突变的适应能力都优于传统LMS算法。其中,改进tanh-LMS算法自适应相位差估计器的稳态失调较小,权值重新调整的速度更快,对时变信号具有更好的跟踪能力。
5 实验验证
为了验证两种改进算法自适应相位差估计器的性能,在实验水池中进行了声学实验。声源采用频率为14 kHz的正弦信号,相邻阵元接收信号的真实相位差为π/6 rad.对直达声信号进行预处理后,作为自适应相位差估计器的输入。基阵接收到的两路原始信号和预处理后的信号曲线如图9所示。

图9 相邻阵元的接收信号曲线
由图9可知,两个自适应相位差估计器的中心频率都与声源相同,其他参数设置保持一致。分别使用改进tanh LMS算法和RLS算法的自适应相位差估计器来测量预处理后信号的相位差,测量曲线如图10所示。

图10 改进算法自适应相位差估计器的估计曲线
由图10可知,两种自适应相位差估计器均能较快收敛,表明两种估计器收敛速度快且稳定性好。经过误差分析,改进tanh-LMS算法自适应相位差估计器的绝对误差为0.078 5°,RLS算法自适应相位差估计器的绝对误差为0.069 9°,因此RLS算法自适应相位差估计器的波动小,估计精度更高。
6 结论
本文针对基于窄带信号的超短基线定位系统相位差估计器存在稳态精度与收敛速度、自适应跟踪能力不可兼得的问题,对自适应相位差估计器展开研究,并通过数值仿真和水池实验结果进行了验证。得到如下主要结论:
1)利用噪声与输入信号间的相关性,对变步长tanh-LMS自适应算法进行改进,提高了LMS算法的抗干扰能力。
2)开展了基于RLS算法的ANF研究,与基于LMS算法的滤波器相比,基于RLS算法的自适应滤波器收敛速度更快和稳态精度更高,不受输入信号的频谱限制。
3)针对信号突变,本文提出的两种改进算法对时变信号有较好的适应性,信号跟踪能力都优于传统LMS算法。
4)将改进tanh-LMS算法的自适应滤波器和基于RLS算法的自适应滤波器应用于超短基线定位系统相位估计算法中,证明了这两种算法的优越性,丰富了超短基线定位系统相位估计算法。
——中国制药企业十佳品牌

