飞行器往复式滑翔延时弹道特性
杨昌志,姜毅,牛钰森,王璟慧
(北京理工大学 宇航学院, 北京 100081)
0 引言
自二战末期德国成功研制“V-1”巡航导弹以来,巡航导弹逐渐成为军事大国的“宠儿”。相比于二战时期,现代巡航导弹以其体积小、质量轻、发射方式灵活度高、打击目标多样性强的特点在现代战争中继续发挥着重要作用[1]。巡航导弹按照战术作用可分为两大类:攻击类巡航导弹和侦察类巡航导弹。其中,如何延长侦察类巡航导弹的飞行时间,提高侦察效率及其对敌方领域的空中压制能力是军事领域的研究热点。针对该问题,国内外学者致力于巡航导弹结构的优化设计研究,通过降低巡航导弹的结构重量或者提高巡航导弹发动机的工作效率以达到延长侦察类巡航导弹飞行时间的目的[2]。然而,考虑弹体结构尺寸及发动机制造工艺水平等因素限制,弹体质量的减轻及其发动机效率的提高有一定局限性。本文基于大自然中鸟类滑翔飞行的原理,创新性地提出一种往复式滑翔盘旋弹道方案以实现延长侦察类巡航导弹飞行时间的目的。
滑翔飞行方式的最大优势在于飞行器可以不依靠自身动力而可以借助气动力实现自身的运动。基于滑翔方式的巨大优势,相关学者已经将滑翔方式应用到各种各样的飞行器中,以实现增大飞行器航程或提高飞行器机动性的目标。在利用滑翔方式提高飞行器航程方面:涂胜元等[3]研究了滑翔方式增大火箭弹航程的可能性,建立了滑翔火箭弹的理论弹道方程,并进行了不同工况下的数值仿真;史金光等[4]研究了滑翔增程弹不同阶段的弹道特性。在利用滑翔方式提高飞行器机动性方面,1933年德国科学家Sanger提出了一种名为“Silverbird”的助推-滑翔跳跃式的新概念飞行器[5];1948年钱学森教授提出一种可以完成洲际飞行的助推-再入大气层滑翔的导弹弹道,也就是后来著名的钱学森弹道[6];孙一博等[7]研究了滑翔飞行器多投放条件下的飞行性能优化问题;王肖等[8]研究了基于准平衡滑翔的解析再入制导方法。进入21世纪以来,关于助推-滑翔式飞行器的研究成果更加丰富:Guo等[9]阐述了动力滑翔机导弹的弹道问题,并分析了其发展的必要性;张元龙等[10]调研汇总了滑翔类飞行器的弹道规划与制导方式;陈思远[11]针对助推-滑翔导弹弹道优化问题给出了一种可行的分段优化方法;何威等[12]研究了滑翔飞行器的再入段弹道特性。综上所述,大多数学者主要研究了滑翔方式对于飞行器的增程效果或滑翔方式对于飞行器的机动性能力提高效果,然而对于利用滑翔方式提高飞行器飞行时间的研究相对较少。
本文提出一种基于亚音速往复式滑翔方式的创新型弹道方案。在该弹道模式下,飞行器不需要借助助推器或者是再入大气层收获较大的速度来实现高超音速滑翔飞行,而是在亚音速的状态下通过自身姿态的调节借助空气动力以实现相应的往复式滑翔弹道飞行,进而实现延长飞行器飞行时间的设计目的。本文参考美军“战斧”巡航导弹BGM-109[13]的模型参数,数值解算飞行器水平盘旋弹道和往复式滑翔盘旋弹道二者的飞行时间差异;在此基础上,研究了飞行器的初始飞行速度和初始弹道倾角对于往复式滑翔盘旋弹道模式飞行时间的影响,为延长侦察类巡航导弹飞行时间提供了一定的理论指导。
1 模型构建
1.1 三维模型
本研究使用的飞行器三维模型如图1所示,主要参考美国海军的“战斧”巡航导弹BGM-109[13]的公开资料。

图1 飞行器三维模型示意图
1.2 计算流体模型
求解飞行器的弹道方程时需要用到升力系数和阻力系数等气动参数,为此本文应用基于计算流体力学(CFD)的数值风洞技术,求得上述飞行器模型的气动参数表。通过网格划分工具软件对包围飞行器三维模型的计算域划分有限体积网格,飞行器表面网格如图2所示。

图2 飞行器表面网格示意图
为验证CFD仿真的有效性,参考Cook等[14]对三维翼型RAE2822的风洞试验结果,通过对比本文针对三维翼型RAE2822气动参数的数值计算结果与风洞试验结果,验证CFD仿真的可靠性。图3为来流马赫数为0.725、攻角为2.92°工况下CFD数值计算结果与风洞试验结果[14]的对比。图3中相对位置是指从来流方向看翼型x轴坐标与翼根弦长的比值。

图3 飞行器翼型表面压力系数数据对比
对比图3中数值风洞结果与试验结果可知,数值风洞仿真结果与风洞试验结果[14]吻合度很高,表明本文选择的数值风洞模型是有效的。
基于数值风洞进而获得了该飞行器的气动参数,主要包括飞行器不同飞行工况下的升力系数和阻力系数,分别如表1、表2所示。

表1 飞行器升力系数表

表2 飞行器阻力系数表
1.3 弹道模型
为研究往复式滑翔方式的延时效率,本文设计了两种飞行弹道,分别是常规的水平盘旋弹道和借助滑翔方式的往复式滑翔盘旋弹道,通过数值弹道解算,对比两种弹道下的飞行器飞行时间,进而分析往复式滑翔盘旋弹道方式提高飞行器飞行时间的延时效率。
1.3.1 水平盘旋弹道
水平盘旋弹道是一种较为常规的飞行弹道,即飞行器抵达目标区域后,飞行器保持一定的速度在某一高度做匀速圆周运动。这一过程中飞行器所受重力、发动机推力和气动力动态平衡,保证了飞行器的速度保持不变;同时这一过程发动机一直处于工作状态,导致飞行器质量的不断变化。为保证实现气动升力抵消飞行器自身重力的弹道设计特点,飞行器的攻角会发生相应改变,进而改变飞行器受到的气动力以适应飞行器重力的变化。水平盘旋弹道方程[15]为
(1)
mg=(Psinα+L)cosγv,
(2)
(3)
[CD,CL]=Coe(v,α),
(4)
D=CDqS,
(5)
L=CLqS,
(6)

(7)
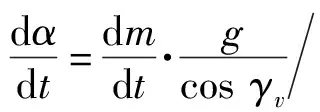
[P(sinαtanα+cosα)+
f′D(α)tanα+f′L(α)],
(8)
(9)
(10)

(11)
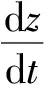
(12)
式中:m为飞行器质量;v为飞行器速度;t为飞行器飞行时间;P为飞行器推力;α为攻角;L、D分别为飞行器受到的气动升力和气动阻力;g为当地的重力加速度;γv为速度倾斜角;R为飞行器的水平盘旋半径;CD、CL分别为飞行器的阻力系数、升力系数,基于表1、表2的气动数据,代入飞行器不同的速度v和攻角α进行插值得到;Coe(v,α)为飞行器的升力系数、阻力系数随飞行速度和攻角变化的函数;q为动压;S为飞行器特征面积;scf为飞行器发动机耗油率;f′D(α)、f′L(α)分别为飞行器气动阻力和气动升力基于飞行器攻角的插值函数关于攻角α的导数;ψ为偏航角;x、z分别是飞行器的二维平面坐标。
水平盘旋弹道的弹道设计特点是,飞行器速度保持不变并保持在某一高度做匀速圆周运动,动力学方程如(1)式~(6)式所示。联立(1)式~(6)式,可求得飞行器飞行过程中的质量m、攻角α、推力P、偏航角ψ以及飞行器运动坐标x、z的微分方程,如(7)式~(12)式所示。
1.3.2 往复式滑翔盘旋弹道
飞行器的往复式滑翔盘旋弹道总体上分为3个阶段,依次是飞行器无动力滑翔盘旋下降阶段、无动力滑翔盘旋上升阶段以及动力助推盘旋上升阶段。无动力滑翔盘旋下降阶段,飞行器最初在某一高度以一定的速度和弹道倾角滑翔盘旋下降,这一过程飞行器发动机处于关机状态,仅依靠飞行器所受气动力和自身重力的调节来实现滑翔过程,并通过改变飞行器的速度倾斜角以改变飞行器受到的气动升力在水平方向的分力,保证盘旋运动的实现。飞行器滑翔盘旋下降至临界高度后,飞行器通过改变气动舵偏角调整飞行姿态进行无动力滑翔盘旋上升阶段。该过程中飞行器的受力状态类似于无动力滑翔盘旋下降阶段,相比于无动力滑翔盘旋下降阶段,不同的是无动力滑翔盘旋上升阶段飞行器在重力和气动力的作用下,飞行器的速度会逐渐降至往复式滑翔盘旋弹道的临界速度。为保证飞行器继续上升,飞行器发动机开始工作进行助推飞行器盘旋上升,飞行器开始进入动力助推盘旋上升阶段,直至飞行器上升至预定的高度后,飞行器调整飞行姿态,飞行器发动机关闭后再次进行无动力滑翔盘旋下降阶段,以此往复,直至飞行器接受到新的飞行指令进而做出飞行状态的改变。
往复式滑翔盘旋弹道相比于水平盘旋弹道的最大区别是:水平盘旋弹道模式下飞行器的飞行高度保持不变,并且飞行器的发动机一直处于工作状态;往复式滑翔盘旋弹道模式下飞行器的纵向运动坐标是在做下降、上升的往复运动,飞行器发动机仅在上升段工作。两种弹道模式下飞行器的纵向运动坐标变化对比如图4所示。
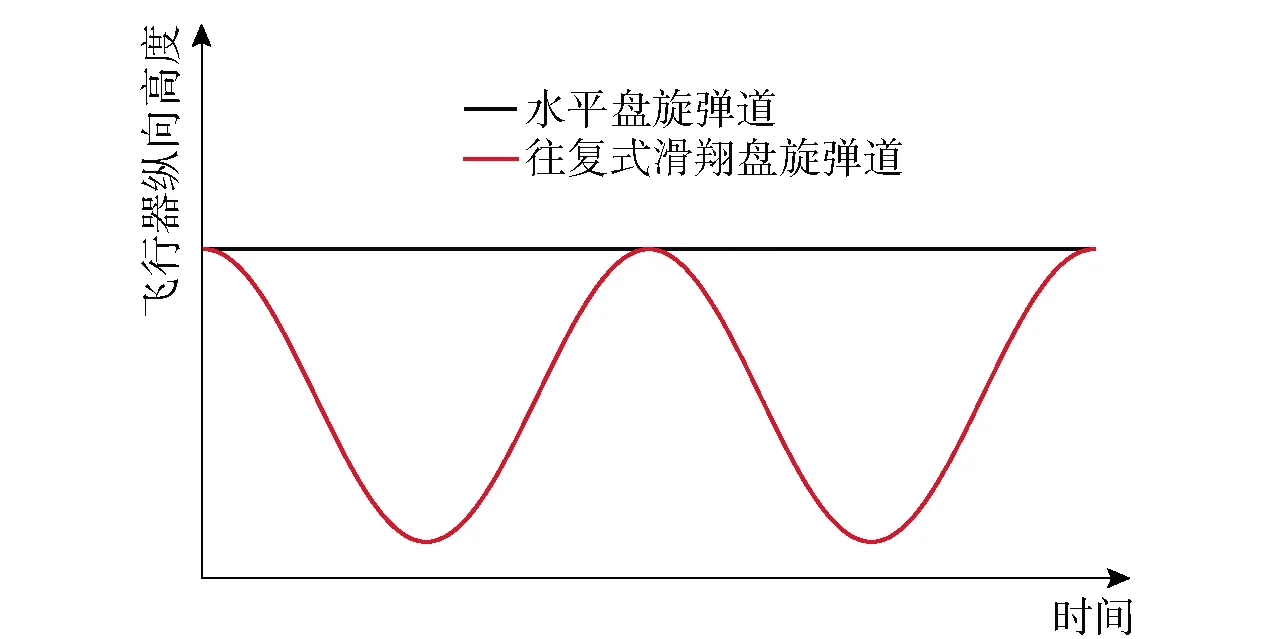
图4 飞行器纵向高度变化示意图
往复式滑翔盘旋弹道整体弹道方程为

Pcos(α+θ)-Dcosθ,
(13)

-Lcosγvcosθ-Dsinθ,
(14)
(15)
(16)

(17)

(18)

(19)
(20)
(21)
[CD,CL]=Coe(v,α),
(22)
D=CDqS,
(23)
L=CLqS,
(24)

(25)
(26)
式中:vh、vv分别为飞行器的水平分速度和竖直分速度;θ为弹道倾角;H为飞行器滑翔期间的高度临界值(飞行最低高度、最高高度等)。
往复式滑翔盘旋弹道的设计特点是飞行器借助气动力和重力的共同作用实现滑翔下降,同时通过调整飞行器速度倾斜角改变飞行器气动力的水平分力,进而保证飞行器滑翔下降的同时也在做水平面的盘旋运动,(15)式体现了这一特点。当飞行器借助气动力无法实现继续上升,发动机开机动力助推飞行器上升,发动机的推力主要受到飞行器当前时刻的速度v、弹道倾角θ以及飞行高度H的调节。当飞行器急需加速上升时,发动机推力增大,当飞行器速度已经足够大时,飞行器发动机的推力会有所减小,尽可能提高发动机的使用效率,(26)式体现了这一特点。
1.4 数值方法
针对1.3节所推演出的两种弹道方程组,本文采用了4阶精度的Adams-Moulton线性多步法[16]求解常微分方程,该方法数值精度较高,在实践中应用很广,算法如下:
设1阶微分方程为

(27)
式中:f为变量χ关于(t,χ)的微分函数。若已知t0时刻的变量值χ0=a0,时间步长h=h0,其中a0、h0是t0时刻的χ变量值以及时间步长,t1、t2时刻的χ变量值a1、a2借助欧拉法或龙格-库塔法求出,χ1=a1,χ2=a2.4阶Adams-Moulton多步法利用求得的χ0、χ1、χ2可求得ti+1=ti+h时刻的χi+1的近似值,公式为

5f(ti-1,χi-1)+f(ti-2,χi-2)],i=2,3,….
(28)
2 计算与分析
本文基于建立的飞行器模型与获得的飞行器气动数据,通过构建不同飞行状态下的弹道方程,结合一定条件下的飞行器弹道设计相关参数[2](见表3),数值迭代求解飞行器往复式滑翔盘旋弹道和水平盘旋弹道模式下各自的飞行时间,研究往复式滑翔盘旋方式提高飞行器飞行时间的效率。在此基础上,研究飞行器的初始飞行速度以及初始下滑弹道倾斜角对飞行器往复式滑翔盘旋弹道延时效率的影响,对其结果进行分析与总结。

表3 飞行器弹道设计相关参数
2.1 往复式滑翔盘旋弹道延时效率研究
通过对比分析不同工况下飞行器水平盘旋弹道和往复式滑翔盘旋弹道的飞行时间,研究往复式滑翔盘旋弹道延时方案的延时效率,计算工况如表4所示。
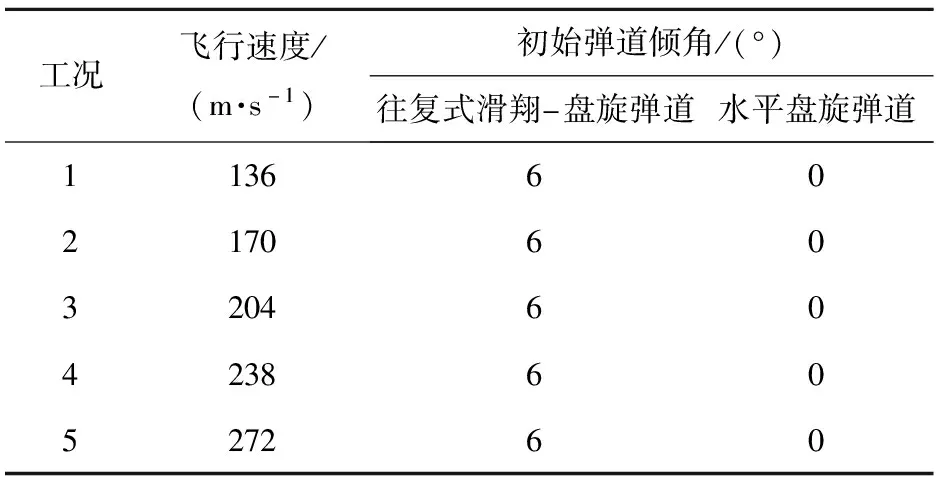
表4 飞行器的不同计算工况
考虑到飞行器往复式滑翔盘旋弹道和水平盘旋弹道的差异,即水平盘旋弹道下飞行器一直保持在某一飞行高度,飞行器的弹道倾角θ等于0°,而往复式滑翔盘旋弹道飞行器处在往复式的下降、上升的运动模式,故选择初始飞行速度v作为工况变量进行计算;针对往复式滑翔盘旋弹道,弹道倾角θ=6°,针对水平盘旋弹道,弹道倾角θ=0°,代入5组工况不同的初始飞行速度,分别进行飞行器往复式滑翔盘旋弹道和水平盘旋弹道模式的弹道解算。
代入不同飞行工况下的初始条件,利用4阶精度Adams-Moulton数值解算程序,最终得到飞行器两种飞行弹道模式下的飞行时间。图5是飞行器水平盘旋弹道结果图,图6是飞行器往复式滑翔盘旋弹道结果图,图7是两种弹道模式下飞行器飞行时间的柱状图对比;表5给出了不同工况下飞行器两种弹道模式的飞行时间对比。

图5 飞行器水平盘旋弹道结果

图6 飞行器往复式滑翔盘旋弹道结果
结合图5、图6可以看出:水平盘旋弹道模式下,飞行器一直保持在某一高度做匀速圆周运动;往复式滑翔盘旋弹道模式下,飞行器在做着滑翔盘旋下降、滑翔盘旋上升以及动力助推上升的往复性运动。从图7、表5中可以清楚地看到飞行器水平盘旋弹道模式和往复式滑翔盘旋弹道模式的飞行时间差异。同一飞行工况下,往复式滑翔盘旋弹道相比于水平盘旋弹道拥有更长的飞行时间,并且随着初始飞行速度的增大,飞行器往复式滑翔盘旋弹道模式下的延时效果愈加明显,在本文列出的5组工况中,当初始飞行速度v=272 m/s时,延时效率达到了1 232.13%.综合分析,随着飞行器飞行速度的逐渐增大,水平盘旋弹道模式下飞行器受到的气动阻力也在逐渐增大,为抵消气动阻力的作用,发动机的推力也在逐渐增大,进而加剧飞行器发动机燃料的消耗速率,导致飞行器水平盘旋弹道的飞行时间减小。

图7 不同工况下飞行器两种弹道飞行时间

表5 不同工况下飞行器两种弹道飞行时间对比
对比5组工况下飞行器两种弹道模式下的飞行时间发现:往复式滑翔盘旋弹道模式下5组工况的飞行时间变化不大,基本都维持在13 300 s附近;而水平盘旋弹道模式下5组工况的飞行时间差距较大。为了避免工况计算的局限性,深入研究往复式滑翔盘旋弹道的延时效率,本文继续研究飞行器水平盘旋弹道模式下最优工况对应的飞行时间。基于(1)式~(6)式,飞行器水平盘旋弹道最优工况对应的飞行速度是在保证飞行器气动升力可以抵消飞行器自身重力的前提下,尽可能减小飞行器的飞行速度以减小飞行器所受到的气动阻力,进而减小发动机的推力,最终实现降低发动机耗油速率的最优飞行速度。通过对表1中飞行器气动升力系数进行数据拟合,可以得到飞行器升力系数关于飞行速度v和攻角α的函数关系式,如(29)式所示:
fL(v,α)=0.000 007v2+0.002 169v·α-
0.001 692v+4.519α+0.415.
(29)
联立(2)式、(3)式可得水平盘旋弹道飞行器速度倾斜角与飞行器速度v的关系为
(30)
对(30)式转换,可得
(31)
考虑到水平盘旋状态下飞行器的攻角α较小,进一步利用sinα=α≈0,同时将(31)式代入(2)式中,可得飞行器自身重力mg与飞行器飞行速度v的函数约束关系为
(32)
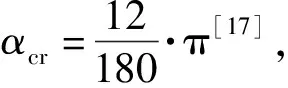
(33)
令
(34)
f(v)在区间v=[20 m/s,180 m/s]内的函数曲线如图8所示。代入表3中弹道设计相关参数,利用牛顿法数值迭代可求解(34)式,得到飞行器水平盘旋弹道的速度最优解为

图8 飞行器不同初始速度的重力约束函数
vo=125.64 m/s.
(35)
将上述求得的飞行器水平盘旋弹道速度最优解vo代入水平盘旋弹道方程解算,可求得飞行器水平盘旋弹道最优飞行时间为11 586.24 s,对比往复式滑翔盘旋弹道的飞行时间均值13 300 s,发现飞行器往复式滑翔盘旋弹道相比于水平盘旋弹道最优解依然能够实现飞行器延时的目的,延时效率可达到14.79%.
2.2 初始参数对往复式滑翔盘旋弹道的影响
在分析了往复式滑翔盘旋弹道模式延时效率的基础上,研究飞行器初始飞行参数对于往复式滑翔盘旋弹道飞行时间的影响。表6给出了研究飞行器初始飞行参数(初始飞行速度、初始弹道倾角)对往复式滑翔盘旋弹道飞行时间影响的25组飞行工况,基于5组飞行速度工况和5组弹道倾角工况。

表6 飞行器工况参数基准
代入表6中的飞行器各种初始飞行参数,进行数值迭代求解,最终得到25组工况下的飞行器往复式滑翔盘旋弹道飞行时间对比,如表7所示。

表7 不同工况下的飞行时间
对比表7中不同工况下飞行器的最终飞行时间,发现在飞行器往复式滑翔盘旋弹道能够实现的前提下,随着飞行器初始飞行速度以及初始弹道倾角的改变,飞行器不同工况下滑翔盘旋弹道下飞行时间差别并不大,基本上都是维持在13 300 s.
综合分析,飞行器做往复式滑翔盘旋弹道时会在气动力和重力的共同作用下做类似匀速盘旋下降的运动,尽管不同工况下飞行器的初始飞行参数不一致,但在飞行器往复式滑翔盘旋的过程中气动力和自身重力的调整下,经过一段时间后不同工况下的飞行器会呈现出相似的运动状态,即不同工况飞行器的飞行时间相差较小。
为验证上述分析,从25种工况中选出2组工况,分别是基于弹道倾角6°的飞行速度工况组和基于飞行速度170 m/s的弹道倾角工况组,具体工况参数如表8所示,图9、图10为9种工况下飞行器的水平速度、竖直速度以及发动机耗油量对比。

表8 飞行器不同初始飞行参数
由图9、图10可以看出:飞行器在最初的运动阶段,飞行器的运动状态变化确实会受到飞行器初始状态的影响,水平速度曲线以及竖直速度曲线均出现了一些上下波动;但经过一定的飞行时间后,不同工况下的飞行器呈现出相似的运动状态,即保持接近的飞行速度作循环往复的往复式滑翔盘旋弹道,飞行器的耗油量曲线变化也呈现出相似的趋势,直至飞行器发动机的燃料消耗完或接受到新的飞行指令才作出飞行状态的改变。综上分析,飞行器初始弹道参数对飞行器往复式滑翔盘旋弹道的飞行时间影响不大。

图9 不同初始飞行速度工况的弹道参数对比
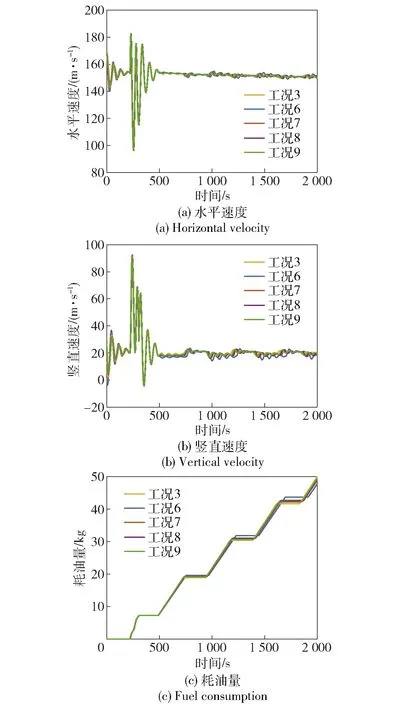
图10 不同初始弹道倾角工况的弹道参数对比
本文在研究飞行器初始飞行参数对于飞行器滑翔盘旋弹道飞行时间的过程中发现,当飞行器的初始飞行速度低于0.3马赫或者初始弹道倾角大于12°会出现飞行器难以实现设计状态下的往复式滑翔盘旋弹道现象,达不到飞行器延时飞行的目的。综合分析之所以出现该现象是由于飞行器的初始速度太小,会导致飞行器的气动力过小,甚至不能抵抗飞行器自身重力,导致飞行器失速,从而加剧了飞行器初始阶段的飞行振荡,最终导致往复式滑翔弹道方案的失败。当飞行器的初始弹道倾角过大时,飞行器竖直方向的速度大小剧增,导致飞行器在滑翔下降至临界高度后仅在自身气动力的调整下难以实现拉起的姿态调整,进而导致滑翔弹道方案的失败。综上,在设计飞行器往复式滑翔盘旋弹道相关初始飞行参数时,应当综合考虑飞行器的气动参数特点,选择相应的弹道参数以保证飞行器往复式滑翔延时弹道方案的成功实现。
3 结论
本文提出一种往复式滑翔盘旋弹道飞行方案,可有效延长飞行器的飞行时间。以美军BGM-109导弹为原型建立飞行器的三维模型,应用数值风洞技术获取升力系数和阻力系数等气动参数。采用4阶Adams-Moulton法求解飞行器的弹道方程组,系统地研究了往复式滑翔盘旋弹道方案的延时效率以及飞行时间与飞行参数之间的关系。得出主要结论如下:
1)相比于飞行器常规的水平盘旋弹道,本文提出的往复式滑翔盘旋弹道可实现更长时间的飞行,且延时效率随飞行速度的增加而提高。往复式滑翔盘旋弹道与水平盘旋弹道油耗最低的理想飞行模式相比,延时效率可达到14.79%.
2)在飞行器往复式滑翔盘旋弹道实现的前提下,不同工况下飞行器在气动力和自身重力的作用下呈现出相似的飞行状态,不同工况下飞行器的飞行时间相差不大,说明飞行器不同的初始速度和初始弹道倾角对飞行器往复式滑翔盘旋弹道的飞行时间影响不大。
3)为确保飞行器往复式滑翔盘旋弹道方案的可实现性,在设计弹道初始参数时应当结合具体飞行器的气动参数特点以及弹道参数设计特点,制定相应的弹道初始参数以保证飞行器往复式滑翔盘旋延时弹道方案的成功实现。

