火炮后效期火药气体流空过程的近似计算方法
缪伟,尹强,钱林方,2
(1.南京理工大学 机械工程学院, 江苏 南京 210094; 2.西北机电工程研究所, 陕西 咸阳 712099)
0 引言
膛内后效时期是指弹丸离开炮口瞬间开始到膛内外流动平衡为止的这个过程[1]。准确计算火药气体的压力及反作用力对包括预估火炮的后坐运动、确定安全的开闩时机、设计炮口装置等火炮设计的多个阶段都有重要意义[2]。
早期的后效期理论建立在准定常假设之上,包括Hugoniot理论[3]和斯鲁霍斯基理论[4]。这些理论采用处理定常流的方法计算膛内气体的空间分布,用平均参数计算气流随时间变化的规律,而平均处理的方法各有不同,这类理论称为准定常理论。郑建国[5]摒弃准定常假设,保留拉格朗日假设,推导了火炮后效期非定常理论计算公式,其理论可视为准定常理论的延续与发展。Corner[6]根据膛内气流的控制方程,考虑膛内膨胀波的传播过程,得出了膛内气体的温度、压力和速度的分布,以及膛底压力随时间的变化规律。由于采用了密度随空间线性变化等假设,Corner得到的结果只能近似地符合膛内气流的分布。此外,Corner方法仅计算到膨胀波第1次抵达膛底前的过程。上述这些方法都是解析方法,它们能够满足工程设计的需求,但是所假设的气流分布与数值解不能严格符合,因此仍存在一定的误差。随着计算机硬件和计算理论的发展,计算流体力学(CFD)方法在后效期计算中得到了广泛应用[7-23]。CFD方法能够得到流场的细节,给出详细的数值结果,然而计算过程通常消耗大量计算资源。
综上所述,后效期过程的关键问题之一是气流的空间分布。本文根据相似性假设得出膛内气流的相似分布及气流参数随时间的变化规律,据此得出后效期炮膛合力的计算公式,针对气流分布向相似分布过渡的过程,给出修正方法。此外,本文根据炮膛合力公式推导了后效作用系数β的计算公式,并将计算公式结果与经典理论计算结果、数值仿真结果进行对比,以验证其有效性。
1 后效期膛内气流的相似性解
文献[10]中图4数值仿真结果表明,后效期中后期膛内气体的密度、速度和压力的分布曲线形状趋近于不变,据此假设膛内气流控制方程存在这样一个相似性解(相似性假设),即气流参数可分解为一个固定不变的空间分布函数与一个时变函数的乘积,称此空间分布函数为后效期相似分布。
1.1 基本假设
在寻找相似性解之前,先给出以下有益的假设:
1)身管是一根等截面的细长圆柱形管道,其左端封闭,弹丸与气体从右端喷出(见图1)。真实火炮的内膛一般包括一段锥形的药室,当药室扩大系数较小时将身管简化成等截面的圆管并不引入很大的误差。

图1 火炮发射过程示意图
2)火药在弹丸射出前即已完全燃烧,火药燃气是理想气体,忽略余容的影响。
3)气体微元各自经历等熵过程,即忽略摩擦等因素引起的热量损失,并且膛内没有出现激波。
4)膛内气体的熵值处处相等,即膛内气流是均熵流动。
5)炮口截面在整个后效期内(包括弹丸通过炮口的时刻)是临界截面,其气流的速度等于当地音速。
6)忽略身管的后坐运动。身管后坐的速度比炮口处的气流速度小两个数量级,因此身管的后坐运动对气流分布的影响很小。
1.2 气流的控制方程及其相似解
根据1.1节假设,膛内气流是一维可压缩无黏流体的非定常流动,其控制方程组为
(1)
(2)

(3)
式中:ρ、u、p分别为气流密度、速度和压力;k为气体的绝热指数;根据等熵假设及气流的均熵性,K为一个不随时间和空间变化的常数。记身管长度为L,引入无量纲坐标s=x/L,s∈[0,1]。根据相似性假设,在t时刻、s处的气流密度、速度和压力可以分别表示为
ρ(s,t)=ξρm,
(4)
u(s,t)=ηum,
(5)
p(s,t)=ζpm,
(6)
式中:ρm、um、pm依次是炮口截面的气体密度、速度和压力;ξ、η、ζ依次是密度、速度和压力的空间分布函数。在不考虑身管后坐运动的假设下,膛底的气流速度应为0 m/s,所以在s=0处,η=0,在s=1处,ξ,η,ζ=1.炮口截面是临界截面,此处气流参数应满足临界关系:
(7)
由气流的均熵性可得
ζ=ξk.
(8)
(4)式~(8)式代入(1)式~(3)式并整理,得
(9)
(10)
(9)式、(10)式左端都是时间的函数而右端都是空间的函数,要使这两个等式恒成立,则等式两端应都是常数。令
(11)
(12)
式中:C1、C2是待定常数。(11)式和(12)式的左边部分决定炮口气流参数随时间的变化规律,右边部分则决定膛内气流的空间分布。
1.3 炮口气流参数
对(11)式和(12)式左边的等式进行积分,得
ρm=ρm0(1+C2um0t)C1/C2,
(13)
um=um0(1+C2um0t)-1,
(14)
根据气流的等熵关系,炮口的压力为
pm=pm0(1+C2um0t)kC1/C2,
(15)
式中:ρm0、um0、pm0是ρm、um、pm在0 s时刻的值,一般后效期的0 s时刻取为弹底通过炮口截面的时刻。
膛内气体的总质量为
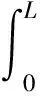
(16)

(17)
整理后,有
(18)
(18)式与(11)式对比,可知
(19)
炮口气流参数(13)式~(15)式代入临界关系(7)式,得
(20)
考虑到临界关系(7)式对包括t=0 s时刻在内的整个后效期都成立,对比(20)式两端的指数,可得
(21)
于是
(22)
则炮口截面的气流参数为
(23)
(24)
(25)
1.4 膛内气流的分布
C1、C2代入(11)式、(12)式,得到描述分布函数形状的积分微分方程组:
(26)
(27)
边界条件为
(28)
这组积分微分方程及边界条件构成了膛内气流分布的边值问题。方程组的解曲线ξ(s)、η(s)分别属于两个曲线族,曲线族的形状因子只有绝热指数k,因而Iξ是k的函数。从方程组(26)式和(27)式中解出导数项,有
(29)
(30)
当k=1时,方程组(29)式、(30)式存在以下满足边界条件的特解:
(31)
(32)
对应的积分为
(33)
当k≠1时,方程组没有显式解,因此寻求数值解。
在右边界处,边界条件ξ=η=1使得方程组的分母为0,因此分布函数在右边界具有奇性。数值求解时采用变步长法从左边界向右进行数值积分。由于右边界处存在奇性,取积分步长充分小处作为近似的积分终点。在得到解之前ξ(0)和Iξ是未知的,所以积分过程需要以迭代的方式进行。数值求解的步骤如下:

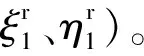



图2绘制了k=1.333时ξ和η的计算收敛过程,停止条件取|εm|≤1.0×10-12时仅需要进行6次积分即可收敛。

图2 k=1.333时密度和速度分布函数的收敛过程

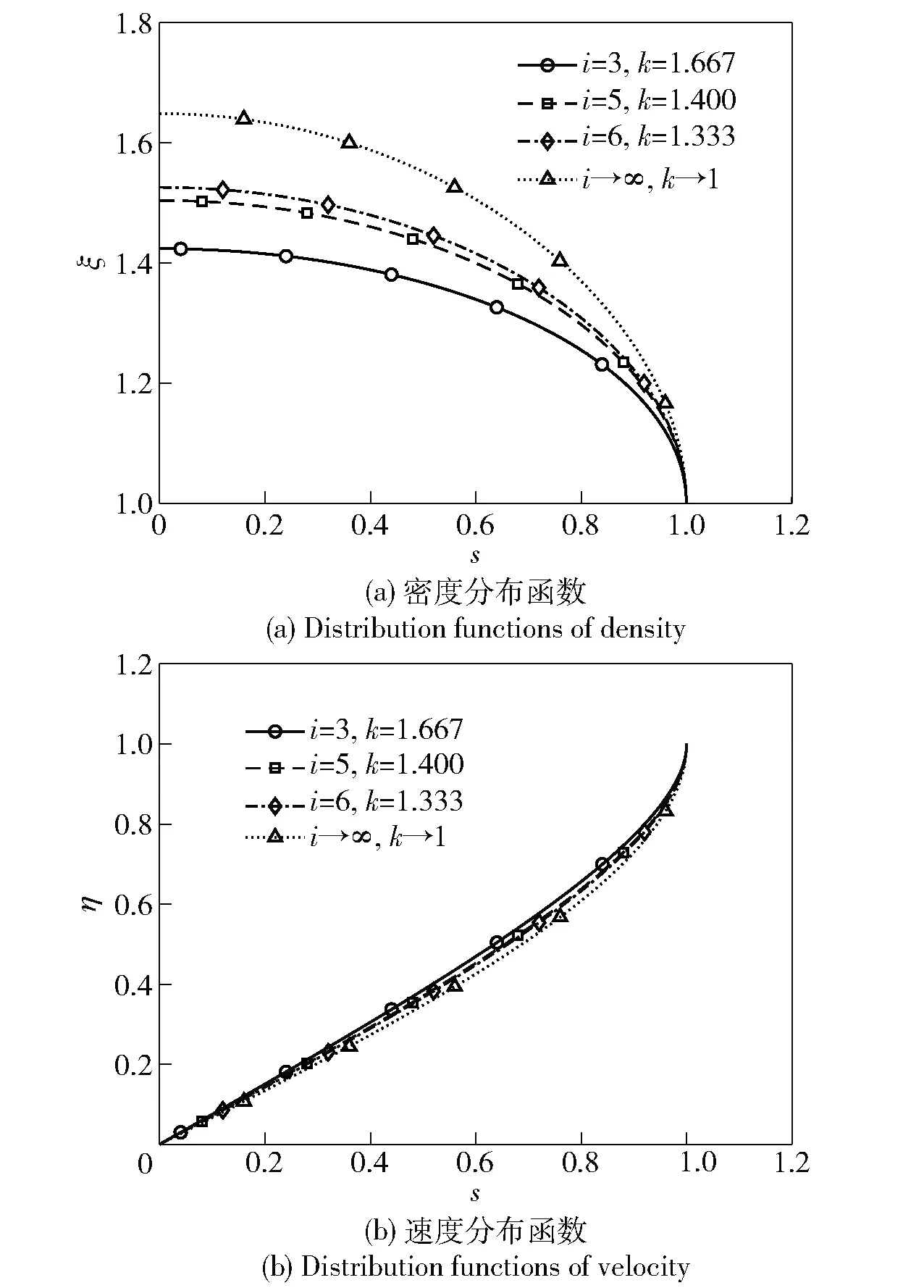
图3 膛内气流密度和速度的分布函数
ξ=exp(a1η4+a2η2+a3),
(34)
s=a4η5+a5η3+a6η,
(35)
式中:拟合系数a1~a6是i的函数,如表1所示。更进一步地,系数a1~a6对i的关系可以拟合成为
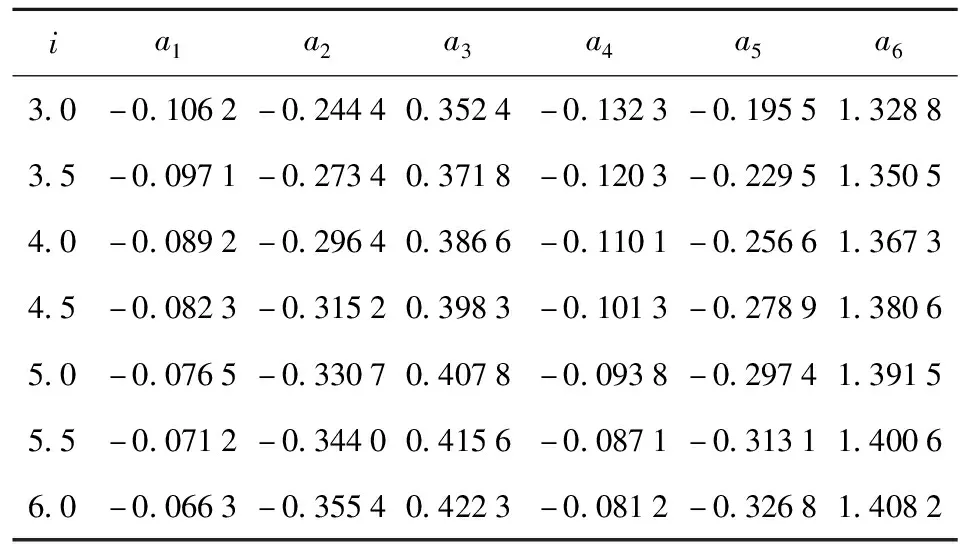
表1 分布函数的拟合系数a1~a6
(36)
式中:系数pj、qj、rj如表2所示。

表2 系数pj、qj、rj
由(30)式可得
(37)
拟合关系(35)式代入(37)式,有
Iξ=a6.
(38)
需要特别说明的是,相似性要求膛内气流分布的形状在后效期内保持不变。而实际上,在后效期开始的瞬间,膛内气流服从内弹道末期的气流分布。在后效期初期,气流分布从内弹道末期的分布逐渐过渡到后效期相似分布,这一过程是由膛内临近炮口截面处产生的原发膨胀在膛内传播与反射实现的。因此不能直接用内弹道时期结束时的炮口参数作为炮口气流参数(23)式~(25)式中的初值,而应该根据守恒律计算ρm0、um0和pm0.此外,内弹道时期的膛内气流通常不能严格满足均熵性,因此对K进行平均处理。本文采用基于密度的加权平均法,则K的平均值为
(39)
式中:mP为发射药的装药量;ρ0和p0分别为内弹道时期结束时膛内的密度和压力。于是炮口截面的气流参数的初值为
(40)
(41)
(42)
至此便可以计算后效期内任意时刻和任意位置处膛内气流的参数。
以上所述膛内气流相似性解的计算步骤可归纳为一个流程框图(见图4)。本文提出的相似性解包括炮口气流参数和气流空间分布函数两部分,其中炮口气流参数随时间变化的规律(23)式~(25)式具有解析的形式,空间分布函数(34)式、(35)式是数值解的拟合公式,因此本文提出的方法属于半解析解法。

图4 气流参数计算流程图
2 后效期炮膛合力与后效作用系数β
火炮气体在后效期对炮身作用的冲量约占火炮后坐总动量的20%,因此,准确地计算后效期内炮膛合力的变化规律,对于火炮的受力和运动计算有着十分重要的意义[24]。
2.1 无炮口装置时的炮膛合力
对于等截面的身管,其不装炮口装置时在后效期内所受的炮膛合力主要来自膛底的气体压力,身管内外表面及炮口端面所受的力很小。膛底的气体作用力为
Fb=Ap|s=0=pmAζ|s=0=
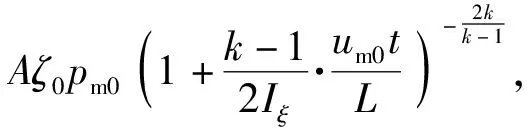
(43)
式中:ζ0=ζ(0)。用拟合公式(34)式近似压力的分布函数ξ,则ζ0=ξ(0)k=exp(ka3)。当k取1.333时,ζ0=1.755.
2.2 考虑膨胀波传播的修正
由1.4节可知,后效期内膛内气流从内弹道末期的分布向后效期相似分布的过渡是逐渐完成的。在此过程中,炮口产生的原发膨胀在膛底和炮口之间往复反射。数值仿真结果表明,在膨胀波第1次抵达膛底时,膛内气流的分布已经十分接近后效期相似分布,此后膨胀波的传播不会对气流分布产生很大的影响。因此本文将后效期分成两个阶段:第1阶段,膛内气流被膨胀波前分成两部分,靠近炮口的部分经历了膨胀波的扰动,而靠近膛底的部分则没有;第2阶段,膛内气流完全服从相似分布。
在第1阶段,膨胀波前面的气体未受扰动,因此它们的运动规律完全由初值决定,这部分气体将延拓内弹道过程。对于一般的枪械和火炮,假设弹丸在穿过炮口后沿着一段虚拟的身管继续内弹道运动,在后效期时间内其速度的增量很小。因此,为了简化计算,认为弹丸在穿过炮口后以速度φv0匀速运动。v0是弹丸穿过炮口时的速度,φ是速度补偿系数,其值略大于1.对于初速高的弹丸,φ应取得小一些,对于初速低的弹丸,φ应取得大一些。这是因为初速低的弹丸在上述假想的运动中获得的速度增量相对更大。这里的初速高低指初速相对弹丸极限速度的大小。综上所述,在膨胀波第1次抵达膛底前,炮膛合力是内弹道过程的延拓,在此之后炮膛合力服从(43)式。
在经典内弹道理论中[25],弹后空间中气体的密度就是平均密度:
(44)
由等熵关系可以得到弹后气流的平均压力为
(45)

(46)
式中:φ1为次要功系数;mS为弹丸质量。由(44)式~(46)式,膨胀波第1次抵达膛底前的膛底气体作用力为
(47)
为了保证膛底气体作用力的连续性,膨胀波第1次抵达膛底的时刻tR由(48)式隐式地确定:
(48)
修正后的膛底气体作用力公式为
(49)
2.3 无炮口装置时的后效作用系数β
后效作用系数是反映火药燃气从膛口高速流出运动对炮身运动影响大小的系数,是火炮设计中的重要参数。它包括内弹道部分和后效期部分:
(50)

(51)
若依据修正的炮膛合力计算公式(49)式,因为后效期被分成两个阶段,则
(52)
2.4 带炮口装置时的炮膛合力
与无炮口装置时相比,加装炮口装置后炮口流场被改变,气流对后坐部分的作用力也随之发生变化。为了保证弹丸安全地飞出,炮口装置的截面总是比身管内膛的截面大,因此加装炮口装置后,炮口截面仍然是临界截面。炮口之外的膨胀扰动不能穿过临界截面传播到膛内,所以炮口装置不改变膛内气流的流空过程,膛底的气流作用力与无炮口装置时的情形并无不同,因此后坐部分受力的改变完全来自炮口装置。
无炮口装置时炮膛合力[4]又可以写为
(53)

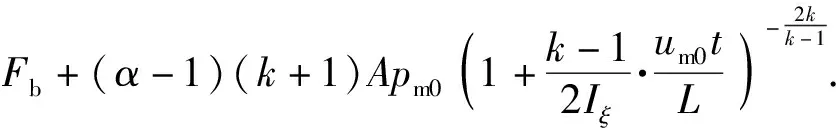
(54)
若考虑2.2节的修正,则将Fb替换为Fb,m.
3 算例
本文以37 mm高射炮[10]和122 mm榴弹炮[16]为例验证本文公式的有效性,这两种火炮分别代表两类火炮,以弹底气流的当地音速计算,37 mm高射炮的弹丸初速是超音速的,而122 mm榴弹炮的弹丸初速是亚音速的。本文参照王杨等[10]的计算方法,用商用流体力学分析软件Fluent的AUSM+格式计算后效期的炮膛流空过程,以数值仿真结果作为对比基准。计算域的构成如图5所示。计算所用参数如表3所示,膛内气流初始条件根据文献[10,16]中的曲线图拟合得到(见表4和表5),膛外大气环境的初始条件为海平面标准大气。

图5 计算域示意图

表3 计算参数

表4 37 mm高射炮后效期膛内气流初始条件

表5 122 mm榴弹炮后效期膛内气流初始条件
在斯鲁霍斯基及郑建国的理论中,火药气体的密度在膛内是均匀分布,速度从膛底到炮口是线性分布。图6中是用本文公式和CFD数值方法计算气流分布的对比,其中数值仿真结果取37 mm高射炮在后效期15 ms时的气流分布,此时膛内气流已充分发展。由图6中可以看出,本文公式求解的相似分布与数值求解的气流分布最接近。
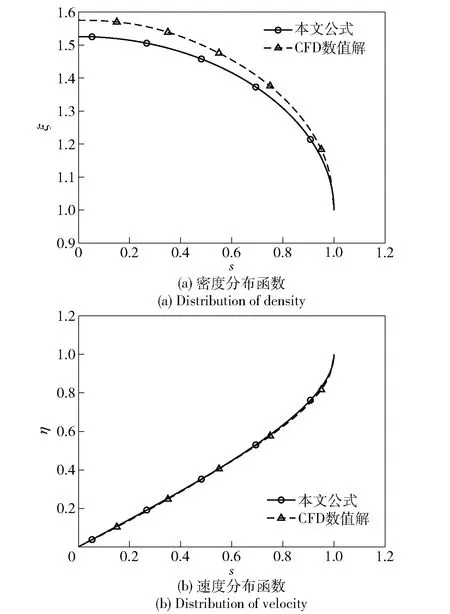
图6 本文公式与数值方法计算气流分布的对比
图7绘制了炮膛内平均密度和平均压力随时间变化的曲线。由图7可以看出,本文公式所计算的平均密度和平均压力介于斯鲁霍斯基公式与郑建国公式[5]的结果之间,37 mm高射炮的结果在5 ms之后、122 mm榴弹炮的结果在整个后效期内与数值解符合得很好。图8对比了37 mm高射炮的炮口压力与数值解、实验测量值[26],三者在后效期内基本符合。上述对比结果表明本文的计算方法有效。

图7 膛内平均密度和平均压力随时间的变化曲线
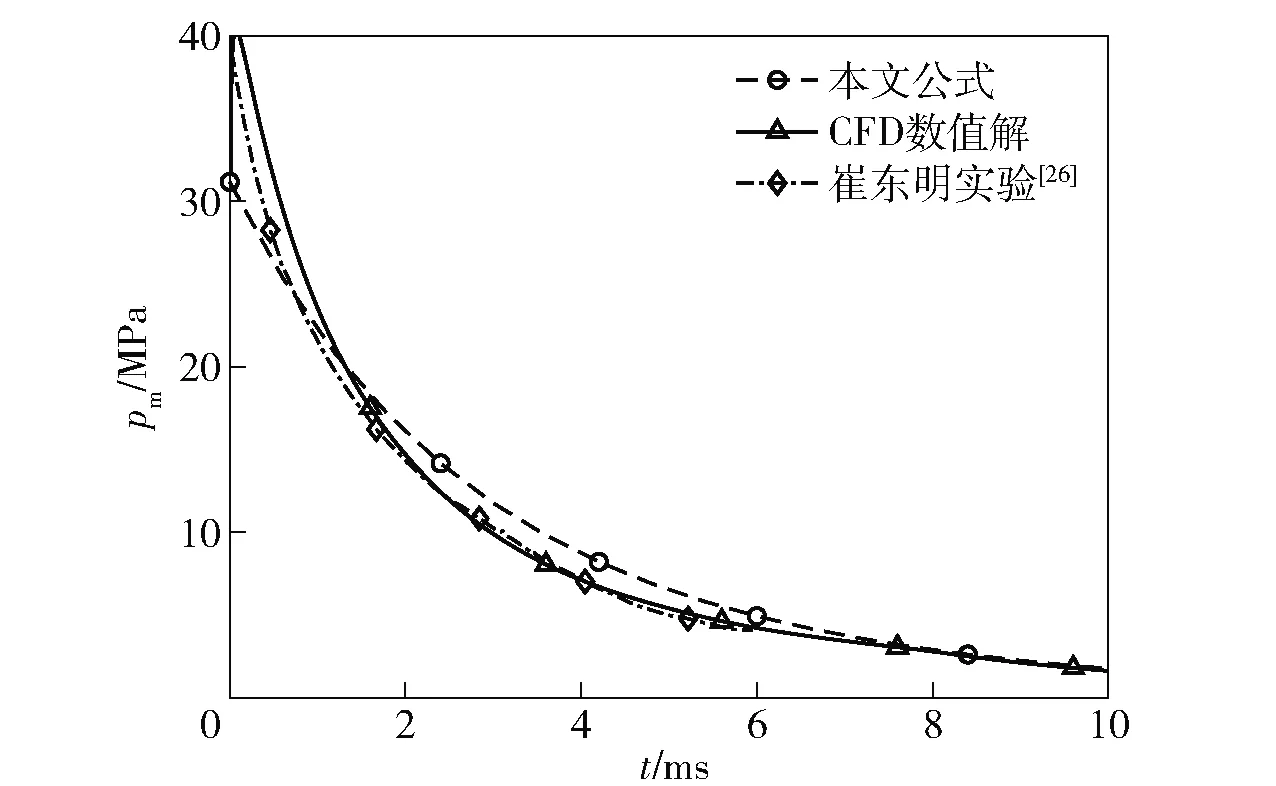
图8 37 mm高射炮的炮口压力
图9绘制了用不同方法计算的后效期炮膛合力。由图9可以看出,CFD方法得到的炮膛合力曲线明显地分成两段。(43)式计算的结果偏离第1段曲线,但是与第2段曲线很好地符合,反映出后效期过渡阶段的存在。
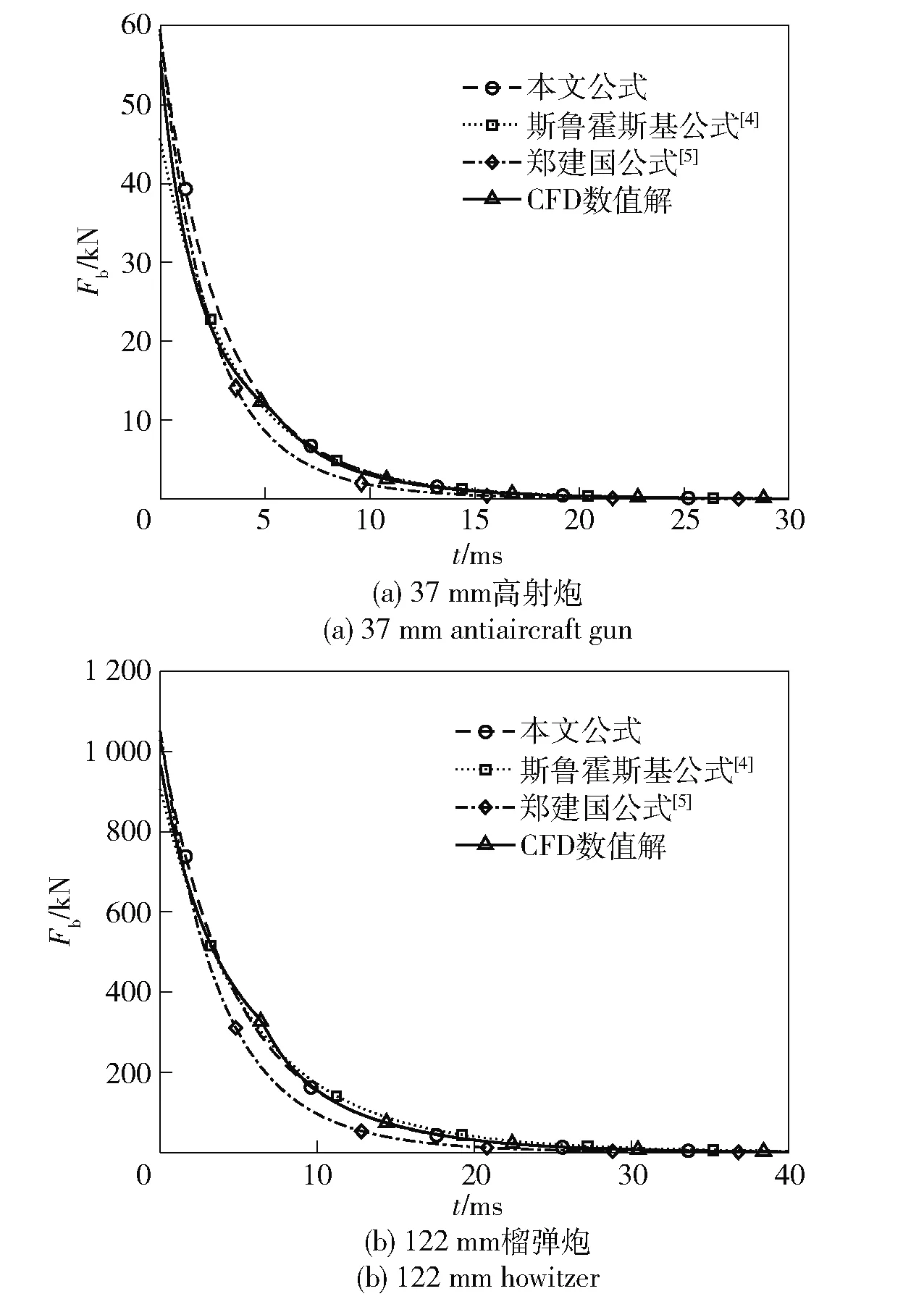
图9 后效期炮膛合力随时间的变化
考虑膨胀波的传播过程并对其进行修正后,由(49)式计算的后效期内炮膛合力与CFD仿真结果的对比如图10所示。在计算时,对于37 mm高射炮和122 mm榴弹炮,本文将速度补偿系数分别取为φ=1.05和φ=1.10.通过对比可得,修正后炮膛合力计算结果与数值解的符合程度得到提升。采用不同方法计算后效作用系数β,结果如表6所示。由表6中可以看出:斯鲁霍斯基公式和郑建国公式计算的后效作用系数均小于CFD结果;而修正前的(51)式过高地估计了后效期气体冲量,其β值偏大,据此进行火炮设计则偏保守;修正后的本文公式计算β与数值仿真结果很接近,相对误差为0.38%~1.80%.

图10 修正后的后效期炮膛合力随时间的变化

表6 不同方法计算的后效作用系数β
4 结论
本文根据后效期膛内气流控制方程的一组相似性解提出了后效期炮膛合力与后效作用系数β的计算公式,并将计算结果与经典公式及数值方法的结果进行对比。与经典公式相比,本文公式有以下优点:
1)本文提出的气流相似分布与充分发展的膛内气流分布更接近。
2)本文提出的炮膛合力计算公式能够与后效期中后期的炮膛合力变化规律很好地符合。
3)考虑膨胀波的传播,修正后的炮膛合力计算公式与后效期炮膛合力变化规律的符合程度得到提升。
4)修正后的本文公式计算的后效作用系数β与数值仿真结果很接近,相对误差为0.38%~1.80%.

