跨速域大后掠角近距耦合翼气动干扰特性

刘清扬，雷娟棉

(北京理工大学 宇航学院, 北京 100081)

0 引言

可回收高超声速飞行器[1-2]目前已经成为各个航天大国的研究热点之一，例如美国2016年为了降低高超声速常规实验成本而建立的HyRAX高超声速可重复使用飞行试验平台和2018年进入轨道飞行实验的XS-1可重复使用高超声速空天飞机。可回收高超声速飞行器在完成高空高速的相关任务后，返回地面的过程中其速度逐渐降低，从高超声速降低到超声速、跨声速、亚声速、低速，再着陆。对采用正常式气动布局的可回收高超声速飞行器来说，在整个飞行过程中，随着飞行速度从高超声速降低到亚声速，前翼对尾翼产生的气动干扰发生变化，使尾翼的气动特性发生变化，对飞行器的飞行稳定性和控制特性都有很大的影响。

高超声速飞行器为了提高巡航飞行器能力，一般采用具有高升阻比的面对称正常式气动布局；为了减小高超声速飞行时的阻力，弹翼和尾舵一般采用具有大后掠角的小展弦比外形[3-5]；为了获得较大的升力和过载能力，需要通过增大翼根弦长来增大升力面积，使得前翼的根弦很长，导致前翼和尾舵之间的距离很小，形成具有大后掠角的近距耦合式气动布局方案。

由于大后掠角弹翼多用于高超声速飞行器，所以研究人员在超、高超声速条件下对大后掠角前翼对尾舵的气动干扰进行了大量的研究。早期由于实验条件的限制以及数值模拟方法的不足，关于后掠主翼和尾舵气动干扰的研究主要集中在马赫数相对较低的超声速条件下。Hart[6]对高超声速翼身组合体复杂干扰现象做了初步分析，在马赫数Ma=2.5的条件下，对两种不同的带有大后掠角前翼翼身组合体分别研究翼身干扰、翼舵干扰等对组合体气动特性的影响，认为通过改变前翼翼后缘形状可以缓解前翼对尾翼的干扰。Leroy[7]对NASA的带后掠角弹翼导弹研究项目进行综述，分析在Ma=2.5条件下弹翼位置对导弹气动特性的影响，研究表明，上单翼布局具有更高的升阻比和更好的俯仰配平特性与方向静稳定性。Blair[8]研究了Ma=3时，后掠三角翼与尾舵间距、上下弹翼位置、多面安装角等参数对高超声速导弹气动特性的影响。

随着实验和数值模拟技术的成熟，国内外研究人员在更高马赫数条件下对大后掠角前翼对尾舵的气动干扰进行了研究。Jerry[9]在Ma=4.63条件下，通过风洞实验研究后掠弹翼对全动舵的干扰特性，提出了翼的遮挡效应。Zhang等[10]研究了高超声速条件下十字形主翼及×形尾翼战术导弹的气动特性，通过数值模拟和实验两种方法对导弹压心位置随攻角的变化进行了研究。Ghoreyshi等[11]研究了大后掠角鸭翼与大后掠角主翼气动干扰特性，展示了高超声速巡航客机有无鸭翼的涡系图。国内外对于大后掠角前翼对尾舵的气动干扰和控制效率的影响进行了一定的研究和实验，但是这些研究基本都是在超声速、高超声速条件下，对于在亚声速、跨声速条件下，大后掠角近距耦合正常式布局中的翼舵干扰问题尚未看到有系统研究的资料。

对具有大后掠角近距耦合翼正常式布局的可回收高超声速飞行器，研究在跨速域不同马赫数和攻角条件下的翼舵干扰气动规律和机理，对飞行器的研制和飞行试验的成功尤为重要。本文对具有大后掠角近距耦合翼正常式布局飞行器的绕流场进行数值模拟，研究亚声速、跨声速、超音和高超声速条件下前翼对尾翼的气动特性干扰规律和机理。本文通过典型算例验证了数值模拟方法的可靠性，分别在有无弹身的情况下，研究跨速域条件下前翼对尾翼的升力、阻力和俯仰力矩特性的影响规律，并通过尾翼表面压力系数和流场结构分析气动干扰机理。

1 数值模拟方法

本文采用有限体积法求解雷诺平均Navier-Stokes(RANS)方程，空间离散和时间离散均采用2阶迎风格式，采用Spalart-Allmaras湍流模型，对大后掠角近距耦合布局流场进行了数值模拟。

1.1 控制方程

本文数值计算采用有限体积法求解RANS方程，三维积分形式的Navier-Stokes方程可以写为

(1)

式中：W、F和G分别定义为

(2)

ρ、E和p分别为密度、单位质量的总能和流体压力，v为流体速度，u、v、w为流体速度分量，τxi、τyi、τzi、τij为黏性应力张量分量，vj为单位速度分量，i、j、k为单位矢量，q为热流通量；V为体积；dA为矢量面积元；矢量H为源项。

1.2 湍流模型

本文数值模拟计算采用了Spalart-Allmaras湍流模型，该模型是一个相对简单的一方程模型，计算量较小，对有逆压梯度的边界层问题能够给出较好的计算结果。

1.3 数值模拟方法验证

本文以文献[12]中美国国家航空航天局进行鸭舵气动干扰试验研究的外形为算例对数值计算方法进行验证，该外形如图1所示为大后掠角近距耦合翼布局，弹身为尖拱形头部加圆柱体形。算例验证取与文献[11]中相同的条件：来流马赫数为0.7、1.2,攻角变化范围为0～20°.图2给出了通过数值模拟得到的算例验证外形全弹升力系数CL和阻力系数CD随攻角变化曲线及文献[11]的试验结果。由图2可以看出，数值模拟计算得到的结果与试验结果均吻合良好，说明用本文数值模拟方法进行具有大后掠角近距耦合翼绕流场模拟计算具有高的可靠性，能很好地进行本文翼舵干扰流动问题的数值研究。

图1 算例验证气动外形示意图

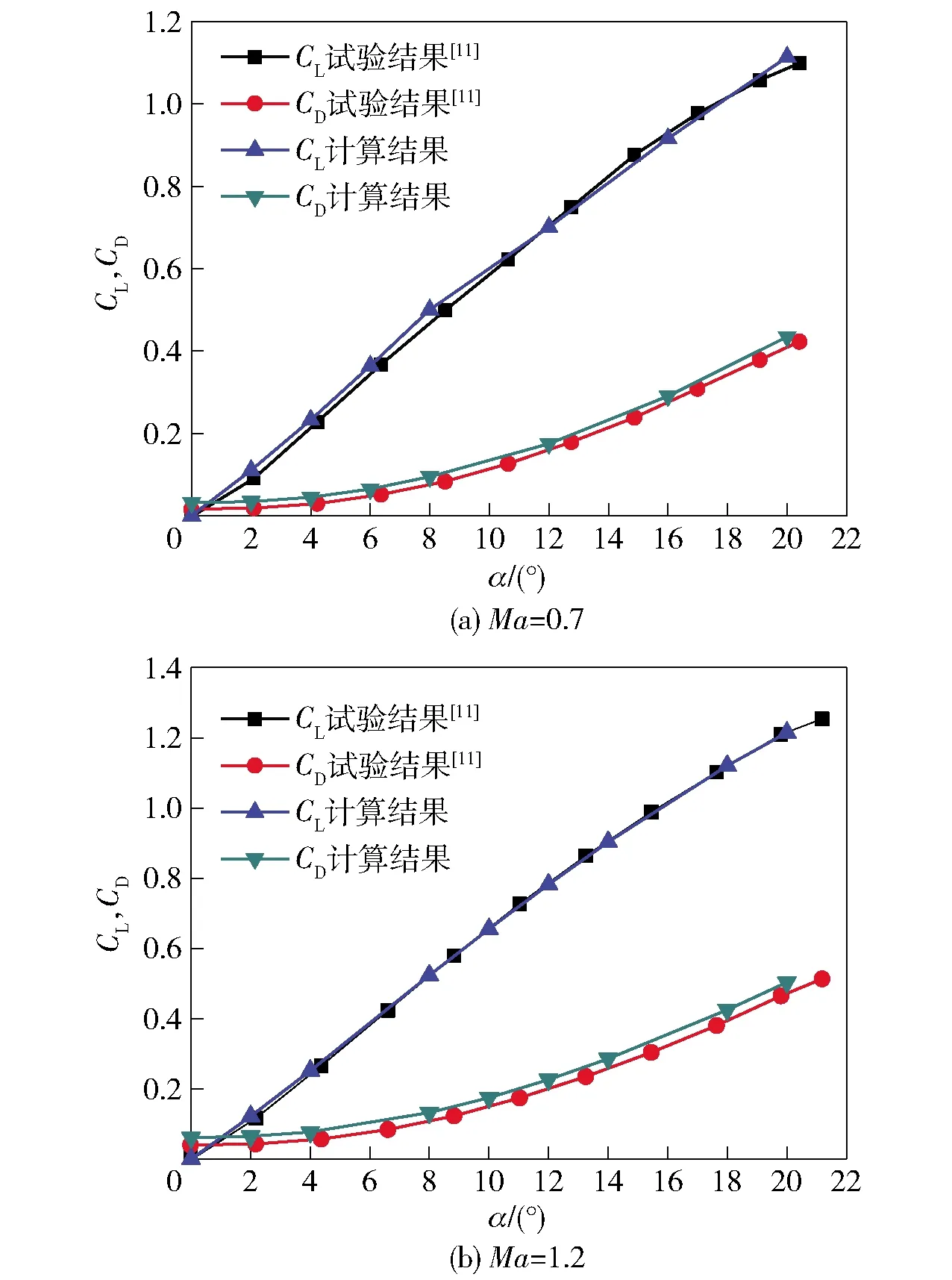
图2 全弹升力系数、阻力系数随攻角的变化

2 数值研究外形及条件

2.1 数值研究外形

本文数值研究的跨速域飞行高超声速飞行器外形如图3所示，为具有大后掠角近距耦合翼的正常式气动布局，只有一对水平弹翼，为面对称外形方案，由弹身、一对水平前翼和十字形的4片尾翼组成。表1给出了不同翼身组合体的示意图，本文重点研究不同马赫数和攻角条件下大后掠角前翼对尾翼气动特性的影响和机理，为排除弹身对前翼及尾翼的气动干扰，首先对前翼+尾翼组合体(简称WT组合体)的绕流场进行了数值模拟计算。为对比分析前翼对尾翼气动特性的影响，还对无前翼的尾翼组合体(简称T组合体)绕流场进行了模拟计算。为分析翼身组合体中翼舵干扰的流动规律和前翼对全弹气动特性的影响，对弹身+前翼+尾翼组合体(简称BWT组合体)和弹身+尾翼组合体(简称BT组合体)的绕流场也进行了数值模拟。表2为本文所研究飞行器各部分的几何参数。

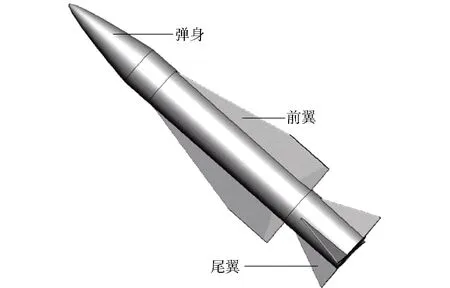
图3 大后掠角近距耦合布局飞行器

表1 翼身组合体示意图

表2 外形几何参数

2.2 计算条件

本文计算条件为马赫数Ma为0.6～8.0,攻角α为5～30°.参考面积Sr=πD2/4，参考长度Lr=LB，D为飞行器弹身直径，LB为弹体长度。

2.3 计算网格及边界条件

本文采用结构化网格对计算域进行离散，在弹体壁面附近等区域对网格进行了加密。考虑到本文中的翼身组合体均为面对称外形，为了提高计算效率，本文沿纵向对称面取半模进行计算。图4为表1中的WT组合体、T组合体、BWT组合体和BT组合体的半模表面和对称面内的计算网格示意图。

图4 翼身组合体表面和对称面内计算网格

数值模拟计算时，计算域外边界采用远场边界条件，弹体表面采用无滑移的固壁边界条件，纵向对称面采用对称边界条件。

3 近距耦合翼跨速域绕流场数值模拟结果

3.1 前翼对尾翼的气动干扰特性

本文首先在不考虑弹身对弹翼和尾翼气动干扰的条件下，对表1中WT组合体的绕流场进行了数值模拟，研究前翼对尾翼的气动干扰特性数值研究。为了更好地分析前翼对尾翼的气动干扰特性，在进行WT组合体绕流场数值模拟的同时，还对表1中T组合体的绕流场进行了数值模拟，得到了两种外形条件下尾翼的气动数据。图5给出了来流分别为亚声速、跨声速、超声速和高超声速典型马赫数条件下，WT组合体和T组合体两种外形条件下尾翼的升力系数CL和阻力系数CD随攻角α的变化曲线。

图5 尾翼升力系数、阻力系数随攻角的变化曲线

由图5可看出：与无前翼的单独尾翼T组合体相比，在同一攻角下，有前翼的WT组合体尾翼升力系数和阻力系数都明显地减小；在同一马赫数条件下，随着攻角的增大，WT组合体尾翼的升力系数和阻力系数的减小量增大。在Ma分别为0.6、1.1的亚声速、跨声速条件下，WT组合体尾翼升力系数和阻力系数显著减小，升力系数的减小量达到50%以上；来流马赫数增大到Ma=3.0的超声速时，WT组合体尾翼升力系数和阻力系数的减小量降低；随着来流马赫数进一步增大，达到Ma=8.0的高超声速时，WT组合体尾翼升力系数和阻力系数的减小量进一步降低；在Ma=8.0且攻角不大于25°的条件下，WT组合体尾翼的升力系数和阻力系数变化量最小。这说明：在亚声速、跨声速、超声速和高超声速条件下，前翼对尾翼都存在洗流干扰；在亚声速、跨声速条件下，前翼对尾翼干扰作用最强，随着马赫数增大，前翼对尾翼的下洗干扰逐渐减弱；在高超声速条件时，前翼对尾翼的下洗作用是最弱的。同一马赫数条件下，攻角越大，大后掠角前翼对尾翼的下洗作用越强。

综上所述，在亚声速、跨声速条件下，前翼对尾翼的干扰作用最强，所以下面以典型亚声速Ma=0.6条件为代表，通过对比有前翼WT组合体与无前翼T组合体尾翼表面压力系数的分布规律，分析前翼对尾翼气动特性变化的影响机理。

为了便于对数值模拟结果进行分析，如图6所示，分别沿尾翼的展向和弦向取不同的剖面，其中L为单独尾翼的展长，C为单独尾翼的弦长。图6(a)中给出了沿尾翼展向3个不同纵向剖面位置，z/L分别为0.2、0.5、0.8；图6(b)给出了沿尾翼弦向4个不同的横向剖面位置，x/C分别为0.1、0.3、0.6、0.9.

图6 尾翼不同剖面位置示意图

图7为在Ma=0.6、α=5°条件下，WT组合体外形和T组合体外形沿展向z/L为0.2、0.5、0.8 3个剖面处尾翼上、下表面压力系数Cp的分布曲线。由图7可看出：与无前翼的T组合体外形相比，有前翼的WT组合体，尾翼展向不同位置上、下表面压差都减小了；相同马赫数和相同攻角条件下，越靠近尾翼前缘，其上、下表面压差的减小量越大。说明WT组合体尾翼展向不同位置均受到了前翼下洗气流的干扰影响，且尾翼前缘附近受到的干扰影响最大。

图7 Ma=0.6、α=5°有前翼和无前翼情况下不同展向剖面内尾翼表面压力系数

图8为在Ma=0.6,α为5°、15°、25°条件下，WT组合体和T组合体在展向z/L=0.5剖面内，尾翼上、下表面压力系数的分布曲线。由图8可知，在同一马赫数条件下，与无前翼的T组合体相比，有前翼WT组合体尾翼上下表面压差的减小量随着攻角增大逐渐增大，导致尾翼的升力系数减小量随攻角增大而增大。

图8 Ma=0.6、不同攻角有前翼和无前翼情况下z/L=0.5剖面内尾翼表面压力系数

图9为在α=25°，Ma为0.6、1.1、3.0和8.0条件下，WT组合体和T组合体在展向z/L=0.2剖面内，尾翼上、下表面压力系数的分布曲线。由图9可知，在同一攻角条件下，与T组合体相比，WT组合体尾翼上下表面压差的减小量随着马赫数的增大逐渐减小，导致尾翼的升力系数减小量随马赫数增大而降低。

图9 α=25°、不同马赫数下z/L=0.2剖面内尾翼表面压力系数

3.2 前翼对尾翼的流场干扰特性

表3为Ma=0.6时WT组合体和T组合体两种外形在不同攻角下沿尾翼弦向x/C为0.1、0.3、0.6、0.9剖面内的流线与压力分布云图。由表3可以明显看出：与没有前翼的T组合体外形相比，有前翼的WT组合体尾翼上表面附近出现了一个明显的旋涡，且随着x/C的增大，尾翼上表面越来越靠近旋涡；在相同攻角和弦向位置处，WT组合体尾翼上表面的压力明显增大，而下表面的压力明显减小，这也是有前翼时，尾翼法向力减小的流动机理。由表3还可看出，攻角增大，WT组合体前翼后脱涡在尾翼区的涡流强度增大，前翼对尾翼的干扰作用增强，这便是3.1节同一马赫数下，攻角越大，WT组合体尾翼的升力系数和阻力系数下降得越多的流动机理。

表3 Ma=0.6时沿弦向不同剖面内尾翼周围流线与压力分布云图

表4为有前翼的WT组合体在不同马赫数和攻角下尾翼弦向x/C=0.1处剖面内的流线图和压力分布云图。由表4可以看出：在Ma为0.6、1.1的亚声速、跨声速条件下，WT组合体尾翼上表面附近出现了明显的旋涡；在Ma=3.0时，尾翼上表面附近的旋涡明显减弱；在Ma=8.0时，尾翼上表面附近没有明显的旋涡。这是因为，亚声速、跨声速条件下，前翼后缘向后拖出的旋涡比较强，到尾翼附近其仍然非常显著；随着马赫数的增大，超声速条件下前翼后脱涡的强度在逐渐减弱；当马赫数增大到高超声速时，在尾翼附近已没有明显的前翼后脱涡。这也是亚声速、跨声速条件下前翼对尾翼气动干扰明显，超声速时前翼对尾翼的气动干扰减小，高超声速时前翼对尾翼的干扰影响很弱的气动机理。

表4 有前翼存在时沿弦向x/C=0.1剖面内尾翼周围流线与压力分布云图

4 有弹身近距耦合翼的数值模拟结果

4.1 有弹身前翼对尾翼的气动干扰特性

为了分析有弹身条件下，从亚声速到高超声速的跨速域范围内大后掠前翼对尾翼的气动干扰特性，对表1中BWT组合体和BT组合体分别在亚声速、跨声速、超声速、高超声速条件下的绕流场进行数值模拟，得到了不同马赫数下BWT组合体和BT组合体尾翼的气动特性计算结果。为对比分析，图10、图11分别给出了Ma为0.6、1.1、5.0条件下，BWT、BT、WT、T 4种组合体尾翼的升力系数、阻力系数随攻角的变化曲线。图12为Ma为0.6、1.1、5.0条件下，BWT和BT组合体尾翼对翼身组合体头部顶点的俯仰力矩系数Mz随攻角的变化曲线。

由图10、图11可知，在亚声速、跨声速、超(高超)声速条件下，有弹身的BWT组合体和BT组合体与无弹身的WT和T组合体相比，尾翼的升力和阻力系数变化规律基本相同。由图12可知，在跨速域条件下，BWT和BT组合体中尾翼对翼身组合体头部顶点的俯仰力矩系数变化规律与尾翼的升力系数和阻力系数变化规律相似。亚声速、跨声速条件下，由于前翼的影响，尾翼的升力系数、阻力系数和俯仰力矩系数都大幅减小，同一马赫数下随攻角增大其减小量增大；随着马赫数增大，有前翼存在时尾翼的升力系数、阻力系数和俯仰力矩减小量降低，到超(高超)声速时，减小量进一步降低，有弹身和无弹身外形的升力系数和阻力系数值也越来越接近。

图10 尾翼升力系数随攻角变化曲线

图11 尾翼阻力系数随攻角变化曲线

图12 尾翼俯仰力矩系数随攻角变化曲线

4.2 前翼对尾翼的流场干扰特性

表5为Ma=0.6时BWT和BT两种组合体在不同攻角下沿尾翼弦向x/C为0.1、0.6、0.9剖面内的流线与压力分布云图。由表5可知，与无弹身组合体相比，有弹身组合体尾翼周围流场变化规律基本相同。有前翼的BWT组合体，尾翼上表面附近出现了一个明显的后脱涡。同一马赫数下，随着攻角增大，前翼后脱涡在尾翼区的涡流强度增大，对尾翼的干扰作用增强，但当攻角比较大时，特别是当攻角增大到25°时，在尾翼附近还出现了新的后脱涡，使得尾翼的周围的流场更加复杂。这是4.1节同一马赫数下，攻角越大，BWT组合体尾翼的升力系数和阻力系数下降得越多的流动机理。

表5 Ma=0.6时沿弦向不同剖面内尾翼周围流线与压力分布云图

表6为来流马赫数为0.6、1.1和5.0条件下，有前翼的BWT组合体在不同马赫数和攻角下沿尾翼弦向x/C=0.1剖面内的流线与压力分布云图。由表6可知，在跨声速条件下前翼产生的后脱涡对尾翼的绕流场有非常大的干扰，当马赫数增加到5.0时尾翼附近已经没有旋涡存在。从亚声速、跨声速到高超声速有弹身的BWT组合体和BT组合体与无弹身的WT和T组合体中前翼对尾翼的流场干扰规律基本相同，所以尾翼的升力和阻力系数变化规律基本相同。

表6 有前翼存在时沿弦向x/C=0.1剖面内尾翼周围流线与压力分布云图

5 结论

本文采用数值模拟方法，在从亚声速到高超声速的跨速域条件下研究了某正常式布局飞行器大后掠近距耦合前翼对尾翼的气动干扰特性，分别给出无弹身和有弹身情况下尾翼升力系数和阻力系数的变化规律及尾翼表面的压力系数，通过尾翼周围的流场结构分析了前翼对尾翼的气动干扰机理。得出以下主要结论：

1)亚声速、跨声速条件下，前翼产生的后脱涡对尾翼的绕流场有非常大的干扰，使得尾翼的上下表面压力差减小，尾翼的升力系数和阻力系数都显著降低。随着攻角的增大，前翼后脱涡强度变大，前翼对尾翼的干扰增强，尾翼的升力系数和阻力系数减小量增大。

2)随着马赫数增大，前翼后脱涡逐渐变弱，对尾翼的气动干扰明显减小。超声速条件下，受前翼干扰影响，尾翼的升力系数和阻力系数减小量降低。高超声速条件下，前翼后脱涡已经消失，对尾翼的绕流场几乎没有什么影响，尾翼升力系数和阻力系数的减小量很小。

3)在亚声速、跨声速、超声速和高超声速条件下，有弹身和无弹身时大后掠角耦合前翼对尾翼的气动干扰规律及机理基本相同。