2.5维编织复合材料经向拉伸弹性性能预测

李居影，李莹，王荣惠，魏化震，孔国强

(中国兵器工业集团第53研究所, 山东 济南 250031)

0 引言

目前，火箭发动机喷管扩散段烧蚀层主要采用高温模压成型的短切碳纤维增强酚醛复合材料。该复合材料具有耐强冲刷烧蚀能力较好、成型工艺简单等优点。但是发动机在连续长时或间歇条件下工作时，扩散段烧蚀层易产生开裂、分层，甚至出现大面积整体脱落的现象，严重影响了发动机工作的安全性能[1-3]。

2.5维编织复合材料具有高强度、高模量、高损伤容限、耐冲击、抗分层和抗疲劳等综合性能，其经纬纱交织结构可以明显改善复合材料层间性能弱的缺点，越来越受到人们的关注[4-7]。但是2.5维编织织物在织造过程中因经纬纱弯曲交联影响织物及其复合材料的力学性能[8-9]，如何设计和优化2.5维编织织物及其复合材料的力学性能成为研究热点。

董伟峰[10]针对2.5维弯联编织复合材料，采用经向纤维束的双凸透镜形，且其中心线沿正弦曲线排布的假设，建立了一种新的有限元模型，并对其弹性常数进行预测，并与试验值进行对比，表明了该有限元模型的正确性。朱永新等[11]采用沿经向切片积分的方法计算2.5维编织复合材料的宏观经向拉伸弹性模量，经纱弯曲程度较小的直联结构和添加平直经纱的衬经结构能够有效提高2.5维编织复合材料的经向拉伸弹性模量，并且能够改善经向拉伸应力-应变曲线的非线性。随着有限元计算方法的发展，Cox等[12]、Xu等[13]、Meglockton等[14]、王新峰[15]、孔春元等[16-17]用有限元方法对2.5维机织复合材料的弹性力学性能进行了计算。

本文采用非线性多尺度材料设计与分析方法，首先输入碳纤维性能参数、树脂基体力学性能参数，创建2.5维编织复合材料的纤维和树脂基体组成相，然后输入编织工艺参数建立复合材料的代表性体积元(RVE)模型，并于一端固定约束，另一端施加准静态拉伸载荷，得到其经向弹性拉伸应力-应变曲线及其应力、应变分布情况。进行弯联结构和直联结构的2.5维编织复合材料试样制备及其拉伸性能表征试验，获得两种复合材料的拉伸应力-应变曲线及其拉伸模量等数据，并将试验结果与仿真计算结果进行对比分析，从而验证了非线性多尺度材料设计与分析方法的有效性。

1 RVE模型的建立

建立2.5维编织复合材料RVE模型是进行仿真计算的基础。本文以国产T800/6k级碳纤维制备的2.5维编织织物为增强体，以含硅芳炔(PSA)树脂为基体制备的2.5维编织复合材料作为仿真计算的初始研究对象。根据国产T800/6k级碳纤维性能参数如密度、纵向弹性模量、横向弹性模量、剪切模量、泊松比等，以及树脂基体性能参数如密度、杨氏模量、泊松比等，建立2.5维编织复合材料的纤维增强体和树脂基体等细观结构的组成相，性能参数如表1所示。

表1 2.5维编织复合材料组成相性能参数

在2.5维编织复合材料纤维增强体和树脂基体等细观结构组成相建立的基础上，按照表2所示的2.5维编织织物的工艺参数，分别构建弯联结构和直联结构的2.5维编织复合材料RVE模型。

表2 2.5维编织织物的工艺参数

图1和图2分别为两种结构2.5维编织复合材料RVE模型，其中红色纱线代表经向纤维(经纱)，蓝色纱线代表纬向纤维(纬纱)。比较图1和图2可以看出：弯联编织复合材料织物的经纱与纬纱交织点较多，经纱屈曲较大，经纱的浮长较短；直联编织复合材料织物的经纱与纬纱交织点稀疏，经纱屈曲较小，经纱的浮长稍长。

图1 弯联2.5维编织复合材料RVE模型

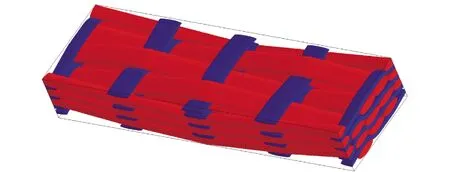
图2 直联2.5维编织复合材料RVE模型

分别对上述两种结构2.5维编织复合材料的RVE模型进行有限元网格的划分，结果分别如图3和图4所示。

图3 弯联2.5维编织复合材料RVE模型有限元网格图

图4 直联2.5维编织复合材料RVE模型有限元网格图

2 RVE模型仿真计算

为得到两种结构2.5维编织复合材料RVE模型的经向拉伸弹性性能，对建立的2.5维编织复合材料RVE模型进行仿真计算。在进行具体的仿真计算工作前作如下假设：

1)假定树脂基体在本次准静态拉伸工况下(RVE模型单元最大拉伸应变为1%)，仅表现出弹性性能。

2)假定纤维与树脂界面的结合完好，暂不考虑界面性能对复合材料整体性能的影响。

3)假定纤维丝束在编织过程中无任何初始损伤，无纤维丝折断等现象。

基于上述假设，利用非线性多尺度材料设计与分析软件，进行两种结构2.5维编织复合材料RVE模型的经向拉伸弹性性能预测。

首先将2.5维编织复合材料RVE模型一端施加固定约束，另一端施加准静态拉伸载荷(拉伸应变设为1%)，拉伸方向沿2.5维编织复合材料的经纱方向(经向)。通过仿真计算得到2.5维编织复合材料RVE模型的平均弹性拉伸应力-应变曲线及其在复合材料模型内部的分布云图。

图5为仿真计算得到的弯联结构2.5维编织复合材料平均弹性拉伸应力-应变曲线。从图5中可以看出，对于弯联结构的2.5维编织复合材料RVE模型，当经向弹性拉伸应变达到1%时，经向弹性拉伸应力达到了265 MPa，计算得知其经向拉伸弹性模量为26.5 GPa.

图5 弯联2.5维编织复合材料RVE模型的经向弹性拉伸曲线

图6为仿真计算得到的直联结构2.5维编织复合材料平均弹性拉伸应力-应变曲线。从图6中可以看出，对于直联结构的2.5维编织复合材料RVE模型，当经向弹性拉伸应变达到1%时，经向弹性拉伸应力达到了1 060 MPa，计算得知其经向拉伸弹性模量为106 GPa.

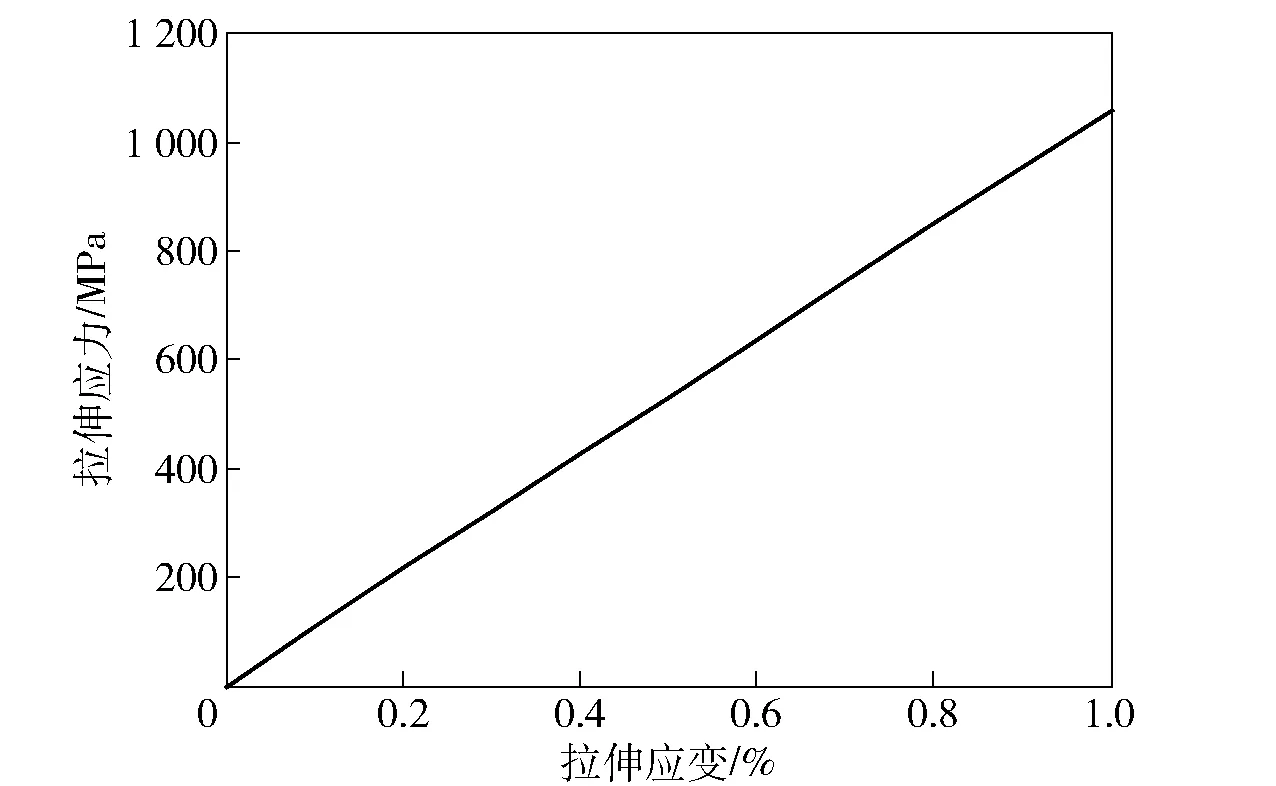
图6 直联2.5维编织复合材料RVE模型的经向弹性拉伸曲线

图7为仿真计算得到的弯联结构2.5维编织复合材料RVE模型的经向弹性拉伸应力分布云图。从图7中可知，当弹性拉伸应变达到1%时，RVE模型内最大应力达到1.51 GPa，且应力较高点主要分布在经纱伸直处，即经纱与纬纱相交区域，纬纱及树脂内的应力水平较低。图8为仿真计算得到的弯联结构2.5维编织复合材料RVE模型弹性拉伸应变分布云图。

图7 弯联2.5维编织复合材料RVE模型的弹性拉伸应力云图

图8 弯联2.5维编织复合材料RVE模型的弹性拉伸应变云图

从图8中可知，模型的最大主应变达到3.3%(本计算过程中暂不考虑破坏)，最大主应变分布在经纱倾斜处，即相邻纬纱区域。初步预测认为，对于弯联结构2.5维编织复合材料RVE模型，当其受到经向拉伸应力破坏时，拉伸破坏首先在相邻纬纱之间出现。图9为仿真计算得到的直联结构2.5维编织复合材料RVE模型弹性拉伸应力分布云图。

图9 直联2.5维编织复合材料RVE模型的弹性拉伸应力云图

从图9中可知，当拉伸应变达到1%时，RVE模型内最大应力达到3.21 GPa，且应力在经向纱线内分布较为均匀。图10为仿真计算得到的直联结构2.5维编织复合材料RVE模型的弹性拉伸应变分布云图。

图10 直联2.5维编织复合材料RVE模型的弹性拉伸应变云图

从图10中可知，RVE模型的最大主应变达到3.7%(本计算过程中暂不考虑破坏)，最大主应变分布在经纱弯曲最大处，即经纱与纬纱相交区域。初步预测认为，对于直联结构2.5维编织复合材料RVE模型，当受到经向拉伸应力破坏时，拉伸破坏首先在经纱弯曲最大处出现。

3 2.5维编织复合材料经向拉伸试验验证

为了验证上述两种结构2.5维编织复合材料RVE模型仿真预测的弹性拉伸模量及拉伸破坏形式准确性，按照国家标准GB/T 1447—2005纤维增强塑料拉伸性能试验方法进行弯联结构和直联结构2.5维编织复合材料试样的经向拉伸性能表征，计算得到了相应复合材料的拉伸弹性模量等试验数据，并获得了两种结构2.5维编织复合材料试样的拉伸应力-应变曲线和拉伸破坏形貌图片。将试验结果与仿真结果进行对比分析，从而验证了2.5维编织复合材料RVE模型仿真方法对复合材料拉伸弹性模量和拉伸破坏形式预测方面的有效性。图11为弯联结构2.5维编织复合材料的拉伸应力-应变仿真结果和试验结果。

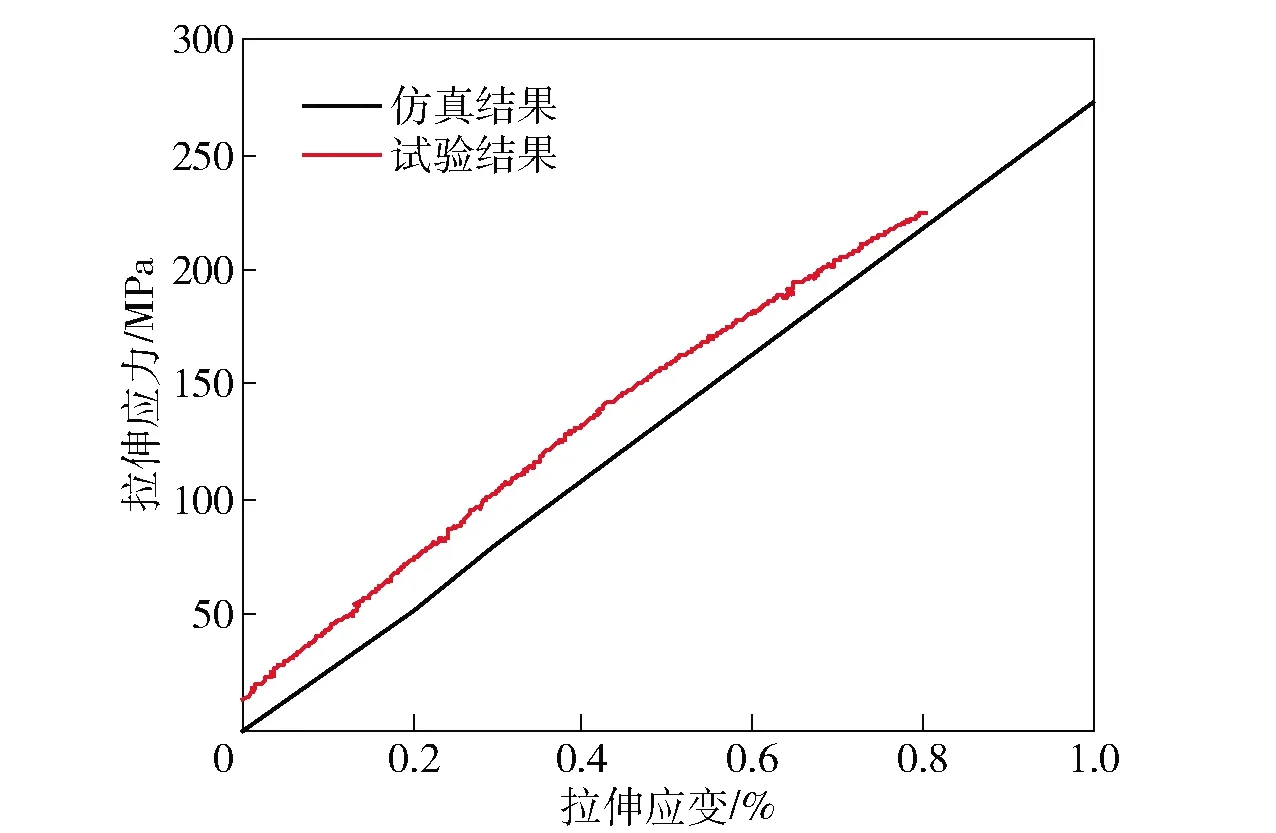
图11 弯联2.5维编织复合材料的拉伸应力-应变曲线

由图11仿真结果可以看出，在0～1%的拉伸应变范围内，该曲线表现出了明显的弹性拉伸特征。分析认为，该弹性拉伸特征主要是由第2节设定的3个仿真计算假设决定的。由图11试验结果可以看出：在0～0.4%的拉伸应变范围内，该曲线表现出了较为明显的弹性拉伸特征；在大于0.4%的拉伸应变范围，该曲线却表现出了较为明显的塑性拉伸特征。分析认为，试验曲线由弹性拉伸阶段向塑性拉伸阶段转变主要是由于树脂基体与纤维的断裂以及树脂基体与纤维基体之间界面的逐渐破坏造成的。

通过比较图11的仿真结果和试验结果还可以看出，两曲线在0～0.4%的弹性拉伸应力-应变过程中吻合度一般，当拉伸应变大于0.4%时，两曲线吻合度趋好。

图12为直联结构2.5维编织复合材料的拉伸应力-应变的仿真结果和试验结果。由图12仿真结果可以看出，该曲线和弯联结构2.5维编织复合材料拉伸应力-应变计算曲线极为相似，在0～1%的拉伸应变范围内，表现出明显的弹性拉伸特征。由图12试验结果可以看出，在0～0.6%的拉伸应变范围内，该曲线表现出明显的弹性拉伸特征，在大于0.6%的拉伸应变范围，表现出明显的塑性拉伸特征。

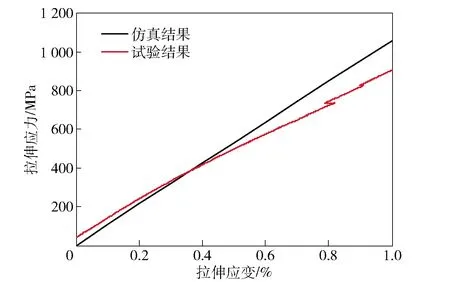
图12 直联2.5维编织复合材料的拉伸应力-应变曲线

通过比较图12中的仿真结果和试验结果可以看出，两曲线在0～0.6%的弹性拉伸应力-应变过程中吻合度较好，当拉伸应变大于0.6%时，两曲线吻合度变差。

通过比较图11和图12的试验结果可知，图12中试验结果的弹性拉伸应变范围更大。分析认为，这主要是因为直联结构2.5维编织织物中沿经纱方向的纤维伸直度比弯联编织织物的伸直度好，经纱与纬纱屈曲降低，而且经纱的浮长增加，在经向拉伸方向上对2.5维编织复合材料力学性能的贡献率更高。这种较为平直的经向纤维编织结构导致了复合材料中树脂基体、纤维以及树脂基体与纤维之间界面的断裂破坏行为延后，相应的曲线弹性应变范围增加[18-19]。

为进一步验证两种结构2.5维编织复合材料在弹性拉伸应力-应变过程中的吻合度差异，进行两种结构2.5维编织复合材料经向拉伸弹性模量试验数据采集，并与仿真计算数据进行对比分析。表3为两种结构2.5维编织复合材料在弹性拉伸应力-应变过程中经向拉伸弹性模量的仿真结果和试验结果。

由表3可以看出：对于弯联结构2.5维编织复合材料，在0～0.4%弹性拉伸应变范围内，其经向拉伸弹性模量仿真计算值和试验测试值的CV值为16.7%，其值超过15%，结果表明，RVE模型仿真计算方法不适用于弯联结构2.5维编织复合材料经向弹性拉伸模量预测；对于直联结构2.5维编织复合材料，在0～0.6%弹性拉伸应变范围内，其经向拉伸弹性模量仿真计算值和试验测试值的CV值仅为3.1%，对比分析认为，采用2.5维编织复合材料RVE模型仿真计算方法可以比较准确地对直联结构2.5维编织复合材料的经向拉伸弹性模量进行预测。

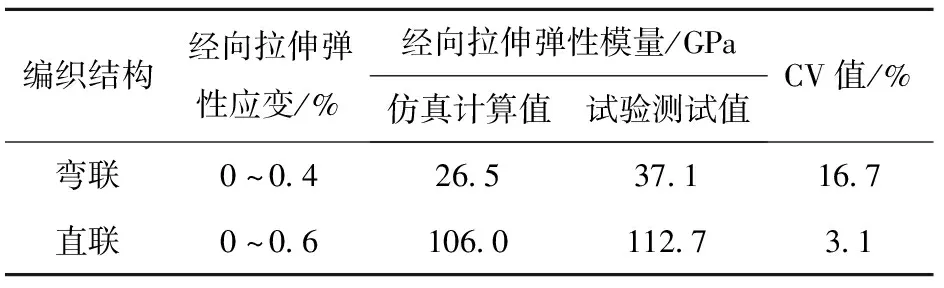
表3 2.5维编织复合材料经向拉伸弹性模量

由表3还可以看出，直联结构2.5维编织复合材料经向拉伸弹性模量高于弯联结构2.5维编织复合材料，前者约为后者的3～4倍。

为进一步验证RVE模型仿真计算方法对2.5维编织复合材料拉伸破坏形式预测的准确性，对两种结构2.5维编织复合材料试样进行了拉伸性能测试和拉伸断裂形貌图像采集，并与通过仿真计算弹性拉伸应变云图预测的复合材料拉伸破坏形式进行对比分析。

图13为弯联结构的2.5维编织复合材料试样的拉伸断裂形貌照片及其对应的相同结构2.5维编织复合材料RVE模型弹性拉伸应变云图。图13中单向红色箭头表示经向纤维方向，双向红色箭头表示复合材料试样断口位置及断裂方向。由图13(a)可以看出，弯联结构2.5维编织复合材料试样的拉伸断面比较齐整，断裂纤维为处于两相邻纬向纤维之间的经向纤维丝束，断裂形式为贯穿式整体断裂，断裂方向沿纬向纤维方向。由图13(b)可以看出，该相同结构复合材料RVE模型弹性拉伸应变云图的最大弹性主应变分布在两相邻纬向纤维(蓝色区域)之间(图中的黄色区域)，即第2节预测的复合材料RVE模型的最先断裂位置。

图13 弯联2.5维编织复合材料的拉伸破坏及预测

通过以上对比可知，对于弯联结构2.5维编织复合材料，其经向拉伸断裂特性如断裂位置、断裂方向的试验结果和仿真计算预测结果非常吻合。分析认为，采用2.5维编织复合材料RVE模型仿真计算方法能够比较准确地对弯联结构2.5维编织复合材料拉伸断裂形式进行预测。

图14为直联结构2.5维编织复合材料试样的拉伸断面形貌照片及其对应的相同结构2.5维编织复合材料RVE模型弹性拉伸应变云图。图14中单向红色箭头表示经向纤维方向，双向红色箭头表示复合材料试样断口位置及断裂方向。由图14(a)可以看出，直联结构2.5维编织复合材料拉伸试样出现了与经向纤维方向呈约30°夹角的拉伸裂纹，无贯穿式拉伸断面产生。由图14(b)可以看出，直联结构2.5维编织复合材料RVE模型弹性拉伸应变云图的最大弹性主应变出现在经向纤维弯曲最大处(红色区域，经向纤维和纬向纤维相交位置)，即第2节预测的复合材料RVE模型的最先断裂位置。通过对出现的经向纤维弯曲最大处(红色区域)进行连线，连线方向(双向红色箭头)基本与经向纤维方向(单向红色箭头)呈约30°夹角。

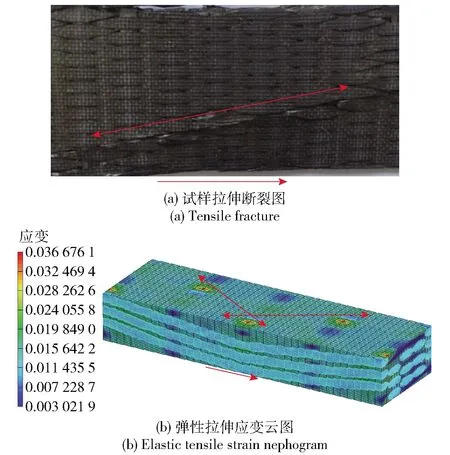
图14 直联2.5维编织复合材料的拉伸破坏及预测

通过以上对比可知，对于直联结构2.5维编织复合材料，其经向拉伸断裂特性如断裂位置、断裂方向的试验结果与仿真结果非常吻合。分析认为，采用2.5维编织复合材料RVE模型仿真计算能够比较准确地对直联结构2.5维编织复合材料拉伸断裂形式进行预测。

4 结论

本文采用非线性多尺度材料设计与分析方法，进行了弯联和直联两种结构2.5维编织复合材料RVE模型的经向拉伸弹性性能仿真计算，并对RVE模型进行了经向拉伸弹性模量和拉伸破坏形式的预测。同时进行了两种结构2.5维编织复合材料试样的经向拉伸性能表征，并与仿真计算的预测结果进行对比分析。得出主要结论如下：

1)采用非线性多尺度材料设计与分析方法，通过2.5维编织复合材料RVE模型仿真计算，可以比较准确地对直联结构2.5维编织复合材料的经向拉伸弹性模量进行预测，其仿真计算值和试验测试值的CV值仅为3.1%；对于弯联结构2.5维编织复合材料，其仿真计算值和试验测试值的CV值超过了15%，表明该计算方法不适用于弯联结构2.5维编织复合材料的经向拉伸弹性模量预测。

2)采用非线性多尺度材料设计与分析方法，通过复合材料RVE模型的弹性拉伸应变云图，可以比较准确地对两种结构2.5维编织复合材料的拉伸断裂形式进行预测。

3)仿真结果和试验测结果均表明，直联结构2.5维编织复合材料的经向拉伸弹性性能要远优于弯联结构2.5维编织复合材料，其中直联结构2.5维编织复合材料经向拉伸弹性模量约为弯联结构的3～4倍。