跨介质航行器高速入水冲击载荷特性

袁绪龙，栗敏，丁旭拓，任伟，周方旭

(西北工业大学 航海学院，陕西 西安 710072)

0 引言

随着现代防御技术的发展，传统的反舰导弹面临突防能力不断被抵消的风险，而鱼雷也因航程短而面临作战效能不足的困境。为了促进导弹武器系统的高速远程优势与鱼雷武器系统的隐身性和毁伤能力优势相融合，跨水空介质航行器概念应运而生。利用超空泡减阻降载技术能最大程度弥合空中飞行与水下航行的速度差距，降低入水载荷，实现空中水下无缝切换，不仅可用于开发新一代高性能武器装备，也能大大提升现有空投鱼雷和潜射导弹武器系统的性能。

本文以一种基于超空泡航行技术的新概念跨介质航行器为对象，研究其高速入水-转平过程的载荷特性。已经开展的原理实验研究表明，为了快速转平而预置的舵角诱发了剧烈的尾拍运动，而尾拍过程产生了巨大的法向过载和弯矩，给航行器结构设计带来挑战。为降低法向过载，有必要系统地开展高速入水转平运动过程中尾拍形成机理及其影响因素研究，从而为消除尾拍振荡、降低法向过载提供指导。关于入水冲击现象的研究，已有很长的历史。1932年，Wagner[1]提出了小倾斜升角模型的近似平板理论,并使得该理论成为现代入水理论研究的基础。Truscott等[2-3]应用空泡截面独立扩张原理分析了射弹入水过程中空泡形态的变化。Lee[4]描述了射弹高速入水的空泡动力学模型，提出了空泡深闭合与表面闭合的概念，发现速度对空泡闭合时间并没有影响。Neaves 等[5]考虑了水的可压缩性，修正了Tait方程并用1阶格式求解出了流场方程，结果与试验结果吻合较好。李国良等[6]对旋成体高速入水可压缩性进行了研究，发现随着入水速度增加,液体可压缩性影响显著，会弱化入水冲击载荷及延缓最大载荷出现的时间。朱珠等[7]运用动网格和用户自定义函数(UDF)技术，计算了柱体高速入水过程，获得了不同工况下的冲击载荷和空泡特性。卢丙举等[8]对细长体航行器高速入水载荷特性进行了研究，发现通气可以显著降低轴向载荷。袁绪龙等[9]通过流场-弹道耦合仿真分析了超空泡导弹在不同预置舵角下的入水过程，发现随着空化器舵角增大，超空泡导弹弹道转平能力增强。钱铖铖等[10]对不同入水角和入水速度的射弹入水进行了仿真分析，得出了射弹最大阻力和阻力衰减速度与弹体入水角度呈正比的结论。汪振等[11]利用数值模拟研究了大口径弹体的高速入水冲击载荷，得出同一速度下轴向载荷峰值随入水角的增加而增加。

综上可见，研究人员对超空泡航行器入水冲击问题已进行了大量研究工作，但在跨介质航行器高速入水和快速转平过程中尾拍振荡引起的巨大法向过载方面研究较少。本文建立跨介质航行器高速入水多相流场与弹道耦合仿真模型，进行详细地验证与校核，然后对典型入水转平过程和不同速度下入水过程进行对比分析，尝试获得跨介质航行器高速入水转平过程冲击载荷特性及其形成机理，为进一步开展降载方法研究奠定基础。

1 跨介质航行器高速入水多相流场仿真模型

本文基于计算流体力学(CFD)分析软件Fluent，采用流体体积(VOF)模型多相流框架，结合重整化群(RNG)模型以及Schnerr and Sauer空化模型进行数值仿真。

1.1 主控方程

高速入水是典型的多相流问题，涉及到空气、水、水蒸气 3相的相互作用。基于均质多相流理论，本文的数值模拟采用VOF隐式模型，由于入水速度高，为了保证计算的收敛，计算中考虑了水的可压缩性。

1.1.1 连续性方程

(1)

(2)

(3)

式中：ρm为多项流混合密度；vm为多相流的质量平均速度；n为多相流的相数；αl为第l相的体积分数，l=1,2,3分别表示气相、水蒸气相和水相；ρl为第l相的密度；vl为第l相的速度。

1.1.2 动量方程

(4)

(5)

vd=vm-vl，

(6)

式中：p为流场中任意点压力；μm为多相流混合动力黏度；vd为第l相与主相的相对速度表达式，对于均匀流动可以不予考虑；S为源相，在广义惯性系中动量方程的源相主要是重力。

1.1.3 能量方程

(7)

(8)

(9)

式中：El为第l相的内能，对于可压缩流动El=hl，hl为第l相的显焓；T为当地温度；SE为体积热源；ke为有效地导热率；kl为第l相导热率；kl为湍流导热率。

1.1.4 体积分数方程

(10)

1.2 湍流模型

RNGk-ε模型改善了ε方程中模拟高应变流动的能力，并且可以通过求解湍流Prandtl数的解析公式得到较为准确的Prandtl数。因此本文选择RNGk-ε湍流模型进行计算，方程中的湍流动能k和湍流动能耗散率ε由(11)式、(12)式两个输运方程联合求解：

(11)

(12)

式中：ρ为流体密度；ui为流体速度分量；P为湍流能项，其由速度梯度引起，

(13)

τij为黏性应力张量，i,j=x,y,z；μ为动力黏度；Pkb、Pεb为湍流能项，由浮力引起；C1ε、C2ε、σk、σε为常数，C1ε=1.44、C2ε=1.92、σk=1.0、σε=1.3；μt为湍流黏性系数。

1.3 空化模型

当前CFD计算中广泛使用的空化模型均是基于输运方程的模型，采用质量源项表示蒸发和凝结过程，以此来模拟水和水蒸气之间的质量传递关系，该方法可以较好地得到空泡的非定常特性。本文计算中使用的空化模型为Schnerr and Sauer空化模型，其具体形式为

(14)

2 运动模型建立与动计算域

2.1 运动模型建立

为描述航行器运动过程，建立图1所示的地面坐标系Oexeyeze和体坐标系Oxyz.

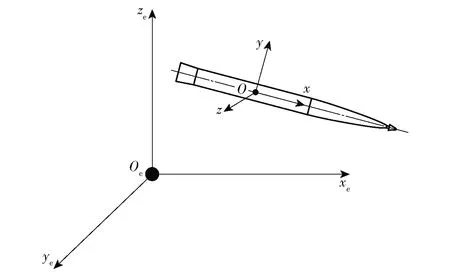
图1 坐标系示意图

2.2 动计算域

本文采用动计算域方法来实现航行器运动过程的网格描述，即通过UDF控制计算域运动，运动过程中网格并不发生变化，变化的是流场域的位置，如图2所示，图中航行器和流场域的相对位置没有发生改变，变化的是整个计算域。

图2 动计算域法运动示意图

入水运动求解过程如图3所示，在每一时间步内，使用UDF提取航行器所受流体动力和力矩，转换到体坐标系下，代入到3自由度(DOF)运动模型中求解出航行器的速度和角速度分量，由Fluent软件完成位置和姿态更新工作。转入下一时间步的计算，直至完成整个高速入水运动过程。

图3 非定常模型求解流程图

3 模型验证与校核

3.1 仿真对象与计算域选择

跨介质航行器外形如图4所示，采用圆锥空化器且带有预置舵角，主体部分有锥台和圆柱组成，圆柱尾部连接一段锥台状扩张裙。

图4 跨介质航行器外形

如图5所示，采用半模计算，计算域尺寸取7 000 mm×2 000 mm×4 000 mm,模型前端距离计算域边界2.5倍弹长，尾部距离计算域边界约4倍弹长，法向边界距离模型轴线24倍弹体直径，设置压力入口和压力出口，边界条件设置如表1所示。

图5 计算域与边界条件

表1 边界条件设置

采用网格生成软件HEXPRESS完成计算域网格划分，对空化器附近、圆柱段、尾裙及尾部后端网格进行加密，如图6所示。

图6 局部网格加密

3.2 网格无关性分析与仿真步长选择

如图7所示，对不同时间步长、单步迭代次数、网格量分别进行了研究。由图7(a)俯仰力矩Mz随时间t变化曲线可见，随着时间步长的减小，仿真结果之间的差异减小，即单调收敛，考虑到计算成本，选用中等时间步长。单步迭代次数和网格尺寸的选择均同此理。

图7 仿真校核曲线

3.3 模型试验验证

为了验证跨介质航行器高速入水数值仿真计算方法的可信性，设计了跨介质入水模型试验，如图8所示，试验模型由斜入水发射装置(见图9)发射进入试验水池，在预置舵角作用下转平。水下高速摄像机记录入水空泡，模型内置的运动测量系统记录弹道数据。

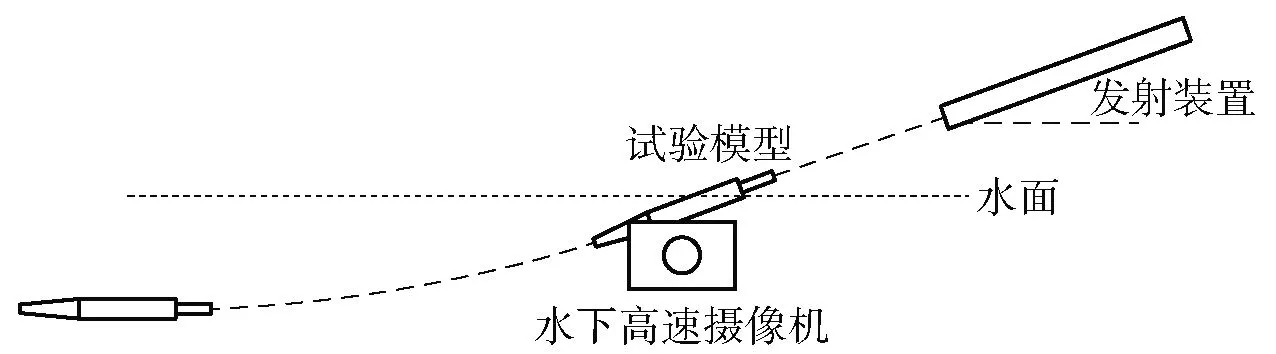
图8 入水试验方案示意图

图9 发射装置

选取入水速度120 m/s、预置舵角7°、入水角15°工况进行了试验。仿真结果与试验数据对比如图10(a)轴向加速度ax曲线和10(b)法向加速度ay曲线所示。试验结果中空化器入水、尾部入水以及模型上下尾拍均产生峰值，其轴向加速度和法向加速度与仿真结果吻合较好。对比图10(c)俯仰角速度曲线可以看出，仿真结果与试验结果的峰值时间对应较好，趋势一致性较好，说明仿真模型设置合理，仿真结果可信。

图10 仿真与试验结果对比

4 仿真结果与分析

4.1 典型入水过程冲击载荷特性

本文以入水角10°、入水速度180 m/s、预置舵角5°作为典型工况进行跨介质航行器高速入水冲击载荷特性研究。图11给出了典型工况下入水-转平过程轴向过载、法向过载、俯仰力矩和攻角变化曲线。

图11 典型工况下过载、俯仰力矩与攻角曲线

结合图12分析，空化器入水后在0.002 11 s形成了一个法向过载峰值，这是由空化器迎流面击水产生的法向冲击力形成的。空化器预置舵角形成的法向力，使模型在入水过程中攻角逐渐增大，迎流面沾湿面积持续增大引起轴向过载持续增大，在尾裙完全入水时(0.006 11 s)达到第1个峰值，同时法向过载也达到峰值。尾裙击水产生的法向力峰值形成了低头力矩峰值(见图11(c))，使得模型低头转动、尾部抬起，在0.008 36 s完全脱离空泡壁，此时，模型仅有头部触水，在预置舵角和攻角共同作用下形成抬头力矩，攻角持续增大，迫使模型快速抬头，尾部下沉第1次拍击空泡下表面，在轴向过载、法向过载曲线上形成冲击脉冲，峰值时刻发生在0.015 11 s.此时，尾部浸水深度达到最大值，法向过载和轴向过载达到峰值，产生的低头力矩也达到峰值。此后，尾部再次弹起，直至离开空泡壁(0.018 61 s)，然后在头部预置舵角作用下，模型再次抬头，尾部第2次拍击下空泡壁。由于速度的衰减，尾拍力度逐渐衰减，模型攻角逐渐减小。

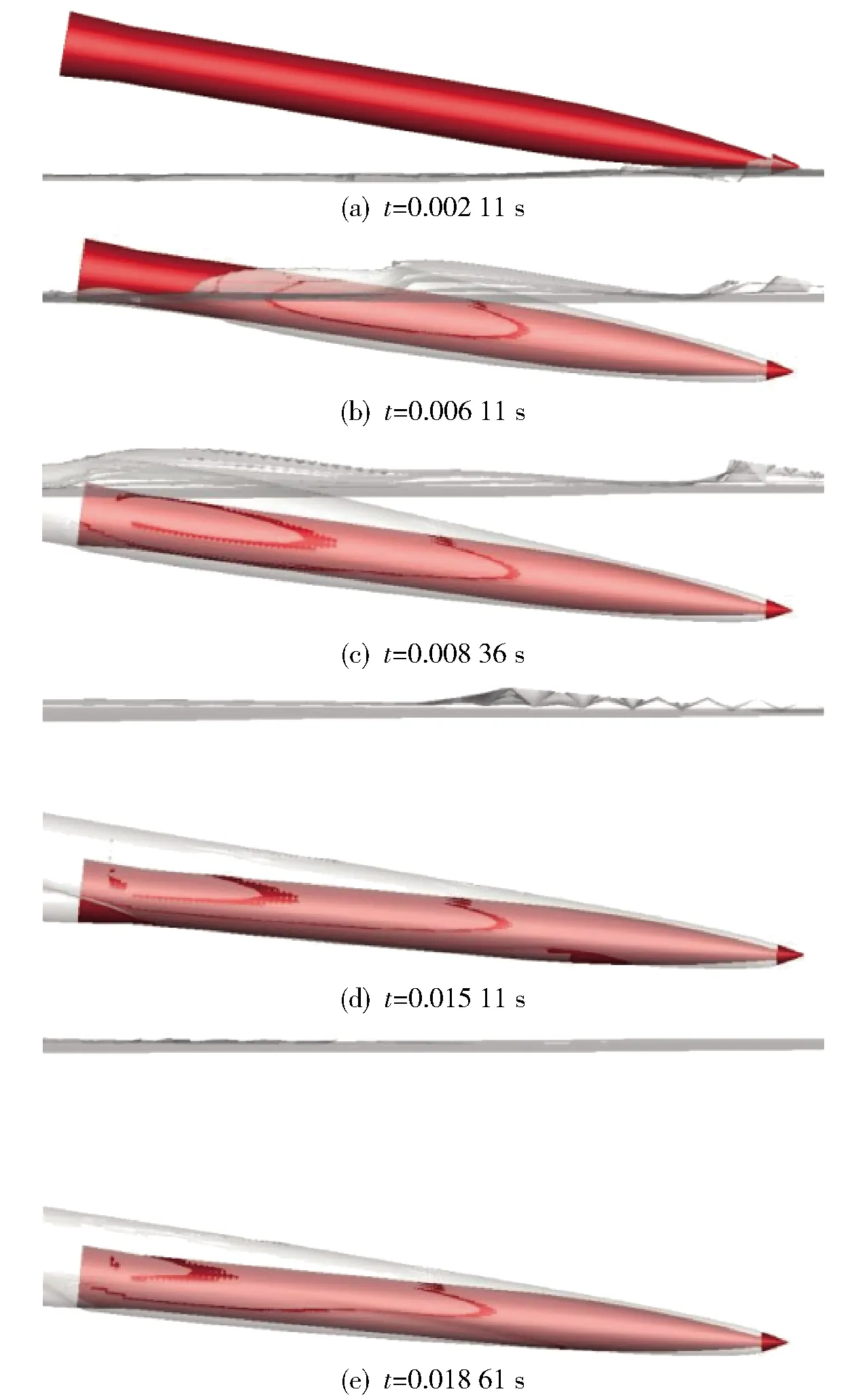
图12 跨介质航行器入水特征时刻的水气界面图

表2列出了各时刻的过载峰值及法向与轴向过载峰值比值。由表2可见，头、尾部入水冲击法向过载是轴向过载值的1.9倍左右，尾拍形成的法向过载是轴向过载的2.7倍左右。头、尾入水冲击时刻形成的法向过载大于轴向过载是由于较小的入水角度造成的，而尾拍产生的法向过载大于轴向过载则是由于尾拍运动速度垂直于航行器轴线。

表2 典型工况下入水特征时刻的载荷峰值点

为了对航行器入水过程中冲击载荷有更清晰的认识，将冲击过程中的轴向力和法向力转化为无量纲系数，并与航行器定常状态下进行对比。

图13给出了入水冲击过程中轴向力和法向力系数曲线。为了分析尾拍产生的升力形成机制(组成成分)，计算尾拍峰值时刻尾部压心处的当地攻角：

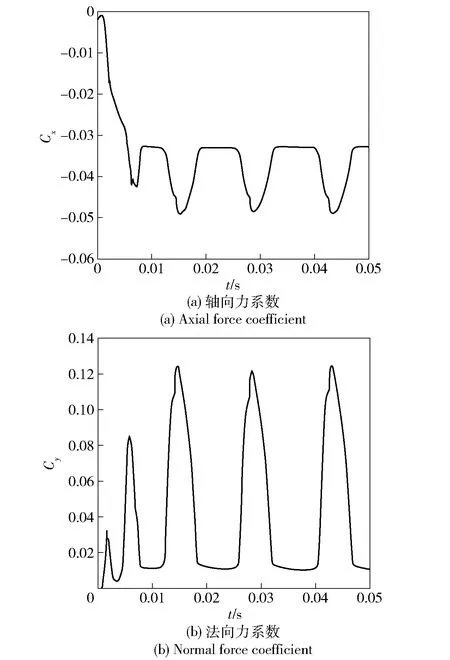
图13 冲击过程中轴向力和法向力系数

(15)

式中：vy为质心处的法向速度；ωz为俯仰角速度；xt(α)为随攻角变化的尾部压心位置；vx为质心处的轴向速度。根据当地攻角αt插值计算轴向力系数Cx和法向力系数Cy.

表3为特征时刻轴向力系数Cx和尾部压心位置当地攻角对应的定常轴向力系数Cx0对比。

表3 典型工况下入水特征时刻的轴向力系数值

结合表3观察图13可见，空化器入水时轴向力系数逐渐增大至0.016，此时空化器仅下表面沾湿，形状阻力很小，随后空泡下表面闭合在锥段并不断后移，锥段沾湿导致轴向力系数继续增大，当闭合位置移动至尾部扩张裙时，轴向力系数快速增加达到第1次峰值0.041，然后尾部向上弹起，航行器尾部悬空时轴向力系数为0.032.随后航行器3次下压碰触空泡壁，轴向力系数峰值均为0.053.整个入水过程航行器轴向力系数较小(0.032～0.053)，超空泡降载效果可观。尾拍引起轴向力系数增大，且峰值小于相同攻角和空化数下的定常阻力系数。

表4列出了特征时刻的法向力系数Cy和尾部压心位置当地攻角对应的定常法向力系数Cy0.由表4可以看出，二者非常接近，因此可以推断尾拍形成的法向力峰值实质上是由尾部当地攻角峰值引起的，而当地攻角由质心攻角和旋转角速度引起的攻角增量组成，其中质心攻角产生位置力，攻角增量产生阻尼力，也就是说尾拍力主要由位置力和阻尼力构成，惯性力很小，可以忽略。这是因为带尾裙航行体尾拍时，只有尾裙下表面沾湿，沾湿面积小，附加质量小到可以忽略。同时也印证了，超空泡状态下阻尼力可由当地攻角计算得到。

表4 典型工况下入水特征时刻的法向力系数

4.2 不同入水速度下过载与冲击力系数分析

图14给出了不同速度下的轴向过载、法向过载、俯仰力矩与攻角曲线。可见，不同入水速度下，航行器均发生了周期性的尾拍现象。具体表现为，航行器尾部拍击空泡下表面，形成正向的法向过载，由于沾湿面增加，形成了同步的轴向过载峰值。在空化器入水、尾部入水和第1次尾拍时，法向过载峰值随速度增大而增大，后续尾拍幅度变化规律不同。法向过载是由法向力引起的，而从4.1节分析可知，法向力是由攻角决定的，因此，从攻角变化规律进行分析(见图14(d))。

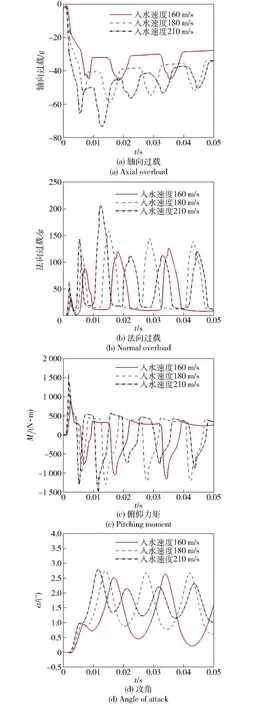
图14 不同入水速度下过载、俯仰力矩与攻角曲线

由图14(d)可见，头部入水时，速度越大，形成的攻角峰值越高、形成时间越早。尾部入水时，尾裙产生低头力矩，短暂地抑制了攻角的继续增大，随后，在头部预置舵角的作用下，攻角快速增大并达到第1个峰值。此时尾部击水深度达到最大，在尾部法向力作用下，快速弹起并离开下空泡壁，攻角减小。攻角减小导致尾部法向力减小，当尾部法向力形成的力矩低于空化器产生的抬头力矩时，低头转动角速度衰减到0°/s，模型达到最小攻角。此时模型在空化器抬头力矩作用下再次抬头转动，开始下一次尾拍过程。第1次尾拍时，速度越高，形成的攻角峰值越大，回弹时的攻角也越大，这是因为速度越高，空化器产生抬头力矩越大，尾部产生相同低头力矩所需的攻角越大。随后攻角变化规律相对复杂，解释如下：尾拍是带空泡航行体在预置舵角引起的阶跃型外部干扰下的系统动力学振荡行为，振幅和频率取决于系统惯性与外力和力矩，不同速度下，系统惯性不变，外力和力矩与速度的平方呈正比，速度越高，振荡频率越高(周期越短，见表5，Δt1～Δt3分别表示3次尾拍的周期)，振幅越低。从攻角振荡曲线可以看出，速度低的振幅大，速度高的振幅小，由于入水后，速度逐渐衰减，所有攻角后续振幅都逐渐增大，振荡周期逐渐增大(见表5)。空化器入水、尾部入水和第1次尾拍时，尚未形成完整的空泡，由于空间位置的关系，其尾拍幅度随入水速度增大而增大。

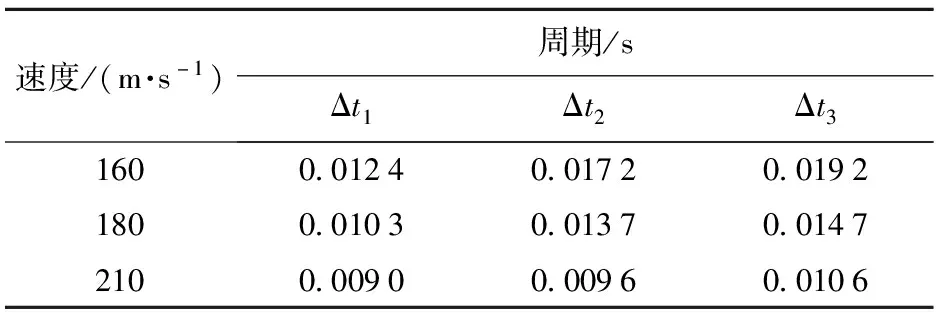
表5 不同入水速度下3次尾拍周期变化表

图15给出不同速度入水过程法向力系数，可见不同速度下，空化器入水、尾部入水、第1次尾拍产生的最大法向力系数相差不大，由法向力系数公式可知，这3种典型入水时刻产生的最大法向力与速度平方呈正比。

图15 法向力系数

表6和表7分别为特征时刻法向力系数及其与尾部压心位置当地攻角对应的定常法向力系数峰值比，可见，尾拍过程的法向力系数基本上是由振荡过程形成的当地攻角引起，由位置力和阻尼力组成，而惯性力(附加质量)可以忽略。

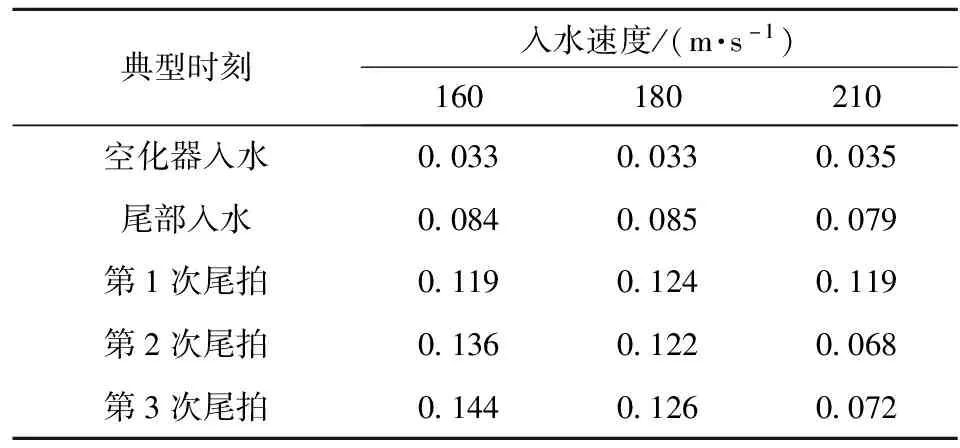
表6 入水特征时刻的法向力系数

表7 入水特征时刻的法向力系数与定常结果比较

5 结论

本文通过数值模拟研究了一种跨介质航行器外形高速入水过程所受的冲击载荷特性，结合运动参数和空泡形态分析了冲击载荷的形成机理。得出以下主要结论：

1)跨介质航行器高速入水转平过程中，形成了尾拍振荡现象。典型入水工况下，空化器入水、尾部入水、尾拍均产生轴向与法向冲击过载峰值，其中第1次尾拍产生峰值最大，空化器入水产生峰值最小。头、尾部入水冲击法向过载是轴向过载值的1.9倍左右，尾拍形成的法向过载是轴向过载的2.7倍左右。

2)小角度情况下，入水过程航行器阻力系数较小(0.032～0.053，约为重型鱼雷阻力系数的1/5～1/3)，超空泡减阻效果显著。尾拍引起阻力系数增大，但峰值仍小于定常状态下阻力系数。

3)尾拍过程法向力系数非常接近尾部压心位置当地攻角对应的定常状态法向力系数，尾拍形成的法向力峰值实质上是由当地攻角峰值引起的，包含了位置力和阻尼力两部分，惯性力可以忽略。

4)随着入水速度的增加，尾拍频率加快，攻角振荡幅度降低，航行器俯仰角振幅减小，本文中带尾裙跨介质航行器入水运动总体上是稳定的。

综上所述，采用超空泡外形的跨介质航行器在高速入水转平过程中，减阻效果显著，也避免了惯性力引起的轴向冲击过载。但是尾拍振荡过程中，产生了较大的法向过载，对弹体结构的影响不容忽视。为了降低法向过载，应设法消除或减弱转平过程中的振荡现象。