间断采样导致末敏弹大范围扫描盲区的消减对策

杨杰，张琪，贺元吉，高洪泉，邓斌

(1.96901部队, 北京 100094; 2.32203部队, 陕西 华阴 714200)

0 引言

在争夺制空权的斗争中，末敏弹是对敌方停机坪飞机实施高精度、高效费比打击的重要手段[1]。打击方案主要有两种：一是通过运载平台在机场上空抛撒有伞或有翼末敏弹，末敏弹在匀速旋转、垂直下降过程中搜索、捕获与攻击目标；二是通过运载平台将自寻的弹丸布散在机场周围，自寻的弹丸发现飞机等装甲目标后垂直抛射无伞无翼末敏弹，末敏弹依靠初始抛出时的高速自旋保持轴向稳定性，在垂直上升与下降过程中搜索、捕获与攻击目标。

末敏弹通常采用占空比作为目标捕获准则，然而该准则受弹目距离、相对姿态影响较大，且易受金属物体干扰[2-3]，导致目标捕获识别概率不高[4-5]。而机场存在大量种类繁多的飞机、车辆及其他金属设备设施，简单的目标捕获准则将使末敏弹误捕、漏捕风险大大增加。基于几何结构[6-8]、特征参数[9]的目标辨识是提高末敏弹捕获目标概率的重要手段[10]。

然而，图像识别、特征匹配等目标捕获准则算法复杂、计算量大。文献[11-13]中试验结果表明，末敏弹线阵列激光雷达图像中目标分离、噪声滤波等处理时间不低于28 ms，基于卷积神经网络的目标辨识时间不低于20 ms，低配置硬件平台辨识时间甚至可达400 ms，此时，末敏弹须采用间断采样目标搜索模式。目前研究仍将间断采样模式下扫描点分布近似为连续采样下的扫描点分布。实际上，间断采样模式下扫描点分布不一定符合螺旋线特征，末敏弹采用等时间间隔采样时，如采样时间间隔满足特定条件，将会出现间断采样导致的大范围扫描盲区现象(以下简称大范围盲区现象)，导致目标漏捕概率急剧增加。

因此，本文通过案例阐述大范围盲区现象的几何特征，从理论上分析无伞无翼末敏弹与有伞或有翼末敏弹大范围盲区现象的形成机制与内在规律，讨论其工程意义，提出减小扫描盲区的对策，并进行仿真评价。

1 末敏弹扫描点轨迹建模

未敏弹的扫描过程[14]如图1所示。图1中，Oxyz为地面坐标系，B、A分别为末敏弹位置、信号波束在地面投影中心点(简称扫描点)位置，θ为末敏弹扫描角，φ、ρ分别为扫描点A的极角与极径，h、v、R分别表示末敏弹的高度、速度、转速。无伞无翼末敏弹迎风面积小、初始转速高，其上升与下降过程可近似为只受重力影响的直线运动且转速恒定，因此，其扫描点轨迹近似为

图1 末敏弹扫描示意图

(1)

式中：v0为抛射速度(m/s)；t为时间(s)；g为重力加速度，g=9.8 m/s2.

由于无伞无翼末敏弹高程不小于0 m，可得

0 s≤t≤2v0/g.

(2)

若末敏弹采用等时间间隔采样模式搜索目标，采样时间间隔为Ts，则t=nTs，代入(1)式可得扫描点集合为

(3)

式中：n为采样序号，

(4)

根据(3)式，可得扫描点集合极坐标形式为

(5)

有伞或有翼末敏弹在稳态扫描阶段可近似为匀速垂直下降运动且转速恒定，同理推导可得，其在等时间间隔采样模式下的扫描点集合为

(6)

式中：H0为末敏弹稳态扫描的初始高度，则采样序号n取值满足：

(7)

根据(6)式，可得扫描点集合极坐标形式为

(8)

定义φ0为标准化极角，与极角φ相差2π rad的整数倍，值域属于[0 rad,2π rad)。

易证，标准化极角φ0与极角φ的关系为

(9)

根据(5)式、(8)式，可得无伞无翼末敏弹与有伞或有翼末敏弹的离散标准化极角φ0(n)均为

(10)

2 大范围扫描现象成因与机理分析

2.1 无伞无翼末敏弹情况

为了描述大范围盲区现象，给出如下仿真案例：

仿真1条件：无伞无翼末敏弹转速R=10 r/s，抛射速度v0=54 m/s，扫描角θ=30°.

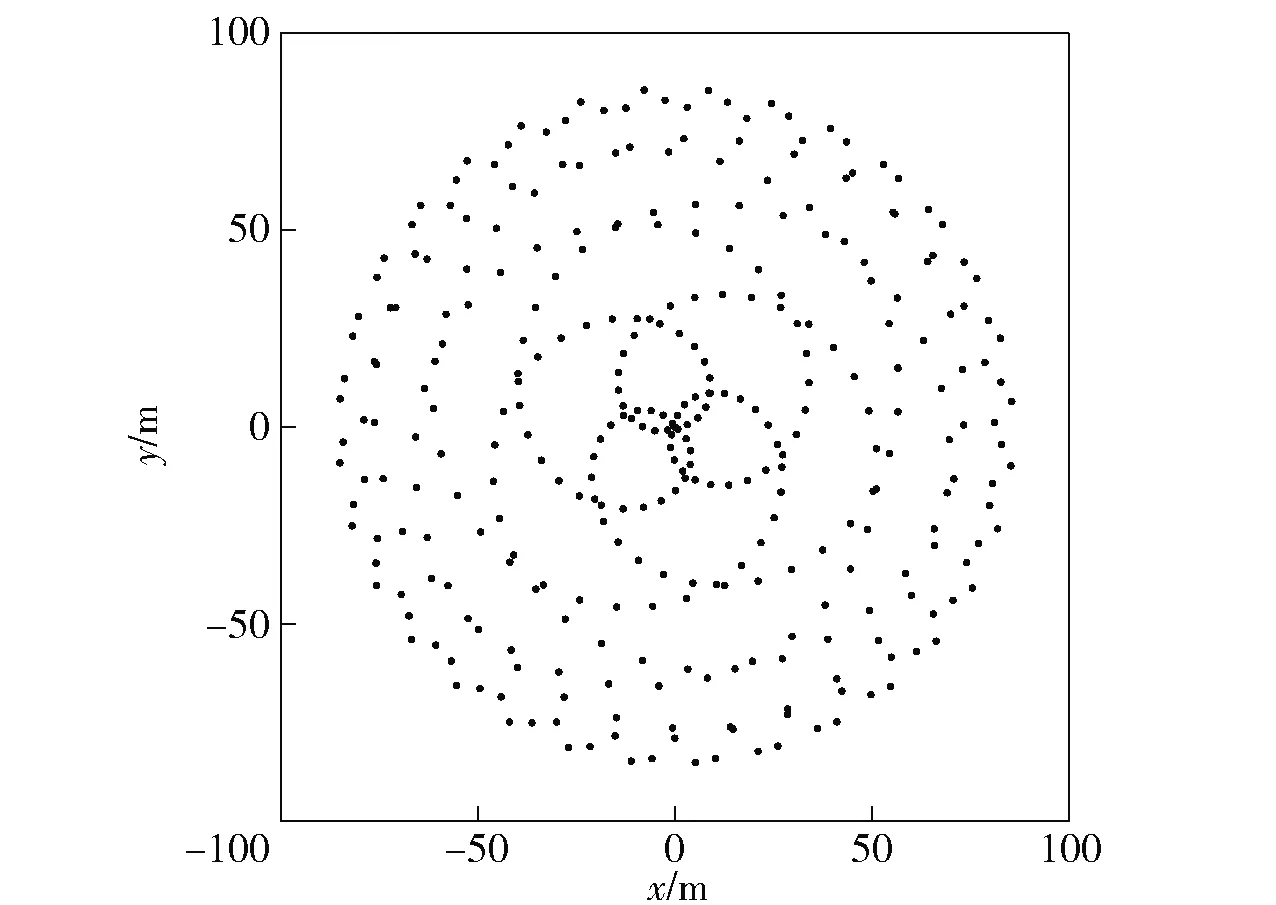
仿真1中，设置采样时间间隔Ts分别取TL、TL+1/2×ΔTN、TL+ΔTN、TL+2×ΔTN，其中，TL、ΔTN分别表示扫描点分布为线性、刚好交叉形状时的采样时间间隔和间隔增量，且TL=3.333 3×10-2s，ΔTN=1.011 2×10-4s.将以上参数代入(3)式，可得末敏弹扫描点集合，如图2所示。

图2 无伞无翼末敏弹在不同采样时间间隔下扫描点集合

由图2可见，该案例扫描点集合不符合螺旋线特点，而表现为若干线段或“叶子”形状，并形成大范围盲区。该现象有两种情况：

1)情况1：离散标准化极角φ0(n)为周期函数，此时扫描点集合形状为若干线段；

2)情况2：离散标准化极角φ0(n)在若干个固定值的基础上周期地、小幅地递进，此时扫描点集合形状为若干“叶子”。

如果该现象导致扫描覆盖区域明显低于连续扫描覆盖区域(即存在大范围扫描盲区)，则称扫描盲区具有显著性，此时目标漏捕概率将大大增加。

针对情况1，本文提出定理1.

定理1离散标准化极角φ0(n)为周期函数的充要条件是，采样时间间隔可表示为

(11)

式中：N0、N1为正整数且互质。

证明先证明充分性。如果采样时间间隔满足(11)式，再结合(10)式，可得离散标准化极角为

(12)

进一步可得

φ0(n+N0)-φ0(n)=0，

(13)

因此，离散标准化极角φ0(n)函数周期为N0.

再证明必要性。如果离散标准化极角φ0(n)为周期函数，由于n是整数，因此周期也是整数，记为M0(M0>0)，则

φ0(n)=φ0(n+M0).

(14)

根据(10)式、(14)式，可得

(15)

令M1=RM0Ts，结合n≥0，可见M1为正整数，易证此时(15)式右侧结果与n的取值无关，即M1是与n无关的常数。因此，有

(16)

对(16)式进行约分即可得到(11)式的对应形式。

定理2如果采样时间间隔满足(11)式，则离散标准化极角φ0(n)的最小正周期为N0，即取值元素数量为N0，且取值集合为{0,2π/N0,…,2(N0-1)π/N0}。

证明根据定理1的充分性证明可知，如果采样时间间隔满足(11)式，则离散标准化极角φ0(n)的周期为N0，再考虑到n是整数，可知φ0(n)的取值数量不超过N0，显然，N0=1时φ0(n)只有取值0.因此只需研究n=0→N0-1(N0>1)时，φ0(n)的取值集合即可。

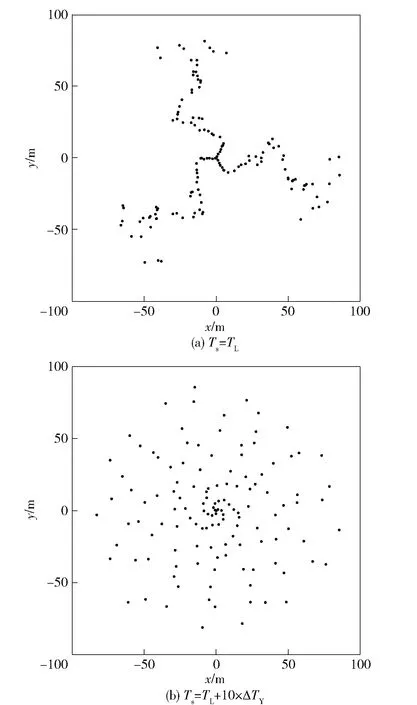
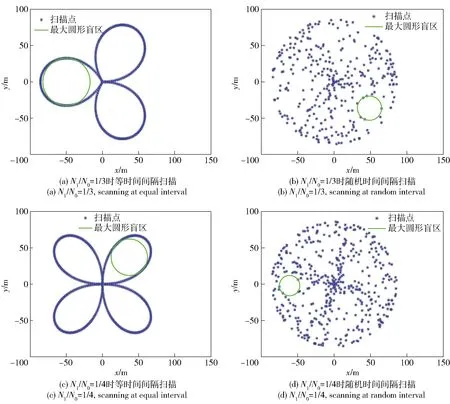
任取满足0≤j

(17)

定义参数：

(18)

由于1≤i-j≤N0-1，N0、N1互质且N0>1，因此，C不可能为整数，(17)式不可能为0，即φ0(i)≠φ0(j)。

因此，n=0→N0-1(N0>1)时，φ0(n)的取值不重复，即取值数量为N0，再结合(12)式可知，φ0(n)的取值集合为{0,2π/N0,…,2(N0-1)π/N0}。

根据定理1、定理2，得如下结论：

1)出现大范围盲区现象情况1的充要条件是采样时间间隔Ts可表示为(11)式；

2)如果采样时间间隔Ts可表示为(11)式，则扫描点集合为N0条角度间隔为2π/N0的线段。

显然，情况2是采样时间间隔在(11)式基础上正向或负向叠加一个小间隔增量ΔT0(ΔT0≥0)，即

(19)

离散标准化极角φ0(n)每前进一个周期(N0个采样点)，就会相对固定值(情况1)递进一个角度增量，呈现为φ0(n)周期地、小幅地递进效果。由于无伞无翼末敏弹扫描点极径按先增后减变化，因此，情况2扫描点集合为“叶子”形状。结合(10)式、(19)式，可得离散标准化极角φ0(n)在单个周期的前进量为

Δφ=2πRN0ΔT0.

(20)

根据(4)式可知，最大采样点个数Nmax为

(21)

则离散标准化极角φ0(n)在单片“叶子”内的最大前进量为

(22)

考虑到情况1中相邻两条扫描线段的夹角为2π/N0，因此，两片“叶子”离散标准化极角φ0(n)无交集(也就是两片“叶子”不交叉)的条件为

Δφmax<2π/N0.

(23)

ΔT0<ΔTN，

(24)

式中：

(25)

考虑间隔增量存在正向与负向叠加两种情况，两片“叶子”不交叉时，采样时间间隔Ts须满足：

(26)

仿真1中，设置N1/N0分别为1/2、1/4，采样时间间隔为TL+ΔTN，其中TL、ΔTN分别按(11)式、(25)式计算，则扫描点集合形状为2片、4片刚好交叉的“叶子”，如图3所示。

图3 扫描点集合形状为2片、4片刚好交叉“叶子”

由图3可见，“叶子”数量由N0决定。“叶子”交叉程度则由间隔增量ΔT0决定，ΔT0越大，“叶子”交叉越厉害，直至难以辨认“叶子”。令N1/N0=1/3，ΔT0=10×ΔTN，仿真结果如图4所示。

图4 3片“叶子”高度交叉

图4中的“叶子”高度交叉，难以辨认，进一步验证了出现大范围盲区现象第2种情况的条件是，采样时间间隔Ts须满足(26)式。

需注意的是，无伞无翼末敏弹由于缺少伞和翼在水平方向减旋，其旋转轴可能不垂直于地面，如图5所示，进而导致其单圈扫描轨迹近似为椭圆[15]。

图5 转轴倾斜于地面时末敏弹扫描示意图

图5中，α表示倾斜角，即末敏弹转轴与地面法向的夹角。可证明，此时末敏弹扫描轨迹方程为

(27)

由(27)式可知，扫描点的极角分布仍然由2πRt决定，因此，旋转轴倾斜于地面时出现大范围扫描盲区现象的条件与旋转轴垂直于地面时相同，只是倾斜角α越大，则扫描点集合形状对称性越差。限于篇幅，本文不再展开讨论。

2.2 有伞或有翼末敏弹情况

参照2.1节分析可知，有伞或有翼末敏弹出现大范围盲区现象的情况1，即扫描点集合形状为线段时，采样时间间隔可表示为(11)式。

由于有伞或有翼末敏弹只有下降过程，因此，出现大范围盲区现象情况2时，扫描点集合的形状为若干“半片叶子”。参照(26)式推导，可得，相邻两个“半片叶子”不交叉时，采样时间间隔须满足：

(28)

式中：ΔTY为相邻两个“半片叶子”刚好交叉时的间隔增量，

(29)

考虑到有伞末敏弹与有翼末敏弹的稳态扫描规律相同，本文只仿真有伞末敏弹的大范围盲区现象。

仿真2条件[14]：有伞末敏弹转速R=4 r/s，初始高度H0=150 m，下降速度v0=14 m/s，扫描角θ=30°.

仿真2中设置N1/N0=1/3，采样时间间隔Ts分别取TL、TL+1/2×ΔTY、TL+ΔTY、TL+2×ΔTY，TL、ΔTY分别按(11)式、(29)式计算，仿真结果如图6所示。由图6可见，有伞或有翼末敏弹与无伞无翼末敏弹出现大范围盲区现象的成因与机制相同。

图6 不同采样时间间隔下有伞末敏弹的扫描点集合

间隔增量ΔT0超过TY时，“半片叶子”之间虽有交叉，但并无交点，而是表现为螺旋纠缠形状。令ΔT0=10×ΔTY、N1/N0=1/3，仿真结果如图7所示。

图7 3个“半片叶子”高度交叉

3 大范围扫描盲区现象的工程意义

末敏弹稳态扫描阶段转速稳定性越好，则引信与战斗部配合效率越高，战斗部定向起爆命中目标概率越大。但工程实际中存在随机气动力矩对转速的干扰，而转速稳定是大范围扫描盲区形成的关键因素，因此需要评估工程实际中扫描盲区现象的显著性。

采用文献[16]中有伞末敏弹的155 mm榴弹炮发射试验数据，转速、扫描角采用32号弹测量数据，落速参考16号弹测量数据并与32号弹测量结束时间对齐，如图8所示，并假设测量结束时间近似为末敏弹落地时间。稳态扫描仿真高度取H0=150 m.

图8 末敏弹扫描参数测量数据

对图8数据分析得到，末敏弹在稳态扫描阶段的转速均值R=3.884 7 r/s，标准差为0.097 0 r/s.令N1/N0=1/3，由(11)式、(29)式计算得到TL=85.8 ms，ΔTY=0.617 2 ms.若末敏弹采取间断扫描模式，采样时间间隔Ts分别取TL、TL+10×ΔTY，由于速度测量值为负值，扫描点坐标计算公式为

(30)

根据文献[16]中试验数据与(30)式得到扫描点分布，如图9所示。

图9 转速波动时不同采样时间间隔对应的扫描点集合

由图9(a)可知，工程实际中转速波动较小时，若采样时间间隔可表示为(11)式或(28)式，仍可出现大范围盲区现象；对比图9(a)、图9(b)可知，该现象对采样时间间隔有较高要求，即采样时间间隔稍有偏离(11)式，扫描盲区显著性会迅速减弱。

进一步分析计算表明，文献[16]试验中，将末敏弹转速的波动放大一倍，则扫描盲区会显著减小，可见大范围盲区现象对于转速稳定性有较高的要求。

4 降低扫描盲区范围的对策研究

4.1 对策的分析提出

由于图像辨识、特征匹配等高复杂度目标捕获准则需要较长的采样时间间隔，因此，扫描点数量有限，如果再出现扫描点聚集的情况(大范围盲区现象本质上是扫描点在某些方向上出现了聚集)，势必会导致目标漏捕风险增大。而理论上讲，只要末敏弹采样时间间隔设计值在(11)式的附近，就有一定的概率出现因大范围盲区现象。为了降低该现象的影响，本文提出如下对策：

对策1采用小采样时间间隔、大敏感器视场角的设计方案。根据(11)式可知，出现大范围盲区现象时，线段或“叶子”及“半片叶子”的数量为

(31)

由上述可见，如果出现大范围盲区现象，小采样时间间隔可有效增加扫描区域的分割数量N0，提高了分割密度，减小了单个盲区的大小。增加视场角则可使扫描光斑面积增大，减小扫描盲区面积。

但末敏弹的低成本、目标的高复杂度特性限制了其采样频率；大视场角则会导致较大的数据处理量，并增大了干扰噪声、降低了目标定位精度[9]。

对策2采用随机采样时间间隔搜索目标，采样时间策略为

t(n+1)=t(n)+Tsε(n)，

(32)

式中：ε(n)为服从区间0.8～1.2均匀分布的随机数。

大范围盲区现象源于等时间间隔采样导致的离散标准化极角周期性，若采用随机采样时间间隔，离散标准化极角便不满足定理1的条件，也就不会有大范围盲区现象。随机采样时间间隔的更深层次意义在于，在扫描点数量不足的情况下，能最大限度地改善扫描点分布的均匀性，避免了扫描点的聚集。该方法对硬件方案改动不大，有较强的实用性。

4.2 对策的效果评价

为了定量评价两种对策对盲区大小的影响，本文在末敏弹的转速、采样时间间隔(随机采样取期望采样时间间隔)、光斑面积均相同的前提下比较两种对策的优劣，并提出盲区半径作为评价指标，即在末敏弹的最大扫描半径范围内，最大圆形盲区(不考虑扫描光斑面积的影响)所对应的半径。

计算如下工况的盲区半径：

1)工况1(大范围盲区现象情况1)：采样时间间隔按(11)式计算；

2)工况2(大范围盲区现象情况2)：采样时间间隔为TL+ΔT0，其中，TL、ΔT0分别按(11)式、(25)式(无伞无翼末敏弹情形)或(29)式(有伞或有翼末敏弹情形)计算；

3)工况3(随机采样时间间隔搜索)：采样策略见(32)式，期望采样时间间隔Ts按(11)式计算，取5次仿真平均值。

易证，3种工况的扫描点数基本一致。

无伞无翼末敏弹在仿真条件1基础上仿真3种工况，得到不同采样方式、采样时间间隔下扫描点集合及最大圆形盲区(见图10)，盲区半径计算结果如表1所示；有伞末敏弹在仿真条件2基础上仿真3种工况，得到不同工况下盲区半径计算结果，如表2所示。

图10 无伞无翼末敏弹扫描点集合及最大圆形盲区

根据图10、表1、表2，可得如下结论：

1)N1/N0减小时，盲区半径随之减小。由于3种工况的转速不变，且N1=1，根据(11)式、(25)式、(29)式可知，N0越大，则采样时间间隔Ts越小，扫描点数越多，对扫描区域的分割越密。可见，减小采样时间间隔可有效降低盲区半径。

2)N1/N0相同时，盲区半径由小至大的排列顺序为工况3、工况2、工况1，且工况3的盲区半径显著小于工况1的盲区半径。工况3在N1/N0=1/2时的盲区半径甚至小于工况1在N1/N0=1/8(见表1)、1/6(见表2)时的盲区半径。可见，采样时间间隔相同时，随机时间间隔采样的扫描模式显著优于固定时间间隔采样的扫描模式。

表1 无伞无翼末敏弹在仿真条件1不同工况下盲区半径

表2 有伞末敏弹在仿真条件2不同工况下盲区半径

如果将盲区半径超过最大扫描光斑(在最高点处)半径作为扫描盲区显著性判断标准，假设末敏弹敏感器视场角为6°[13]，则进一步仿真可得，为避免显著性扫描盲区，有伞末敏弹与无伞无翼末敏弹在工况1均需满足N0≥27(即采样频率至少要达到转速的27倍)，而在工况3只需满足N0≥16(有伞末敏弹)、N0≥9(无伞无翼末敏弹)。因此，随机采样策略所需期望采样时间间隔远大于出现大范围盲区现象时所需采样时间间隔，这大大降低了末敏弹图像辨识的硬件要求。

综上所述，随机采样策略在基本不改变末敏弹原有硬件方案的条件下，有效地降低了大范围盲区现象引起的盲区半径。因此，对策2优于对策1.

5 结论

随着目标复杂度的提高以及干扰技术的发展，基于图像识别、特征分析的目标捕获准则成为末敏弹技术的重要发展方向，间断采样也成为重要的目标搜索模式，由此带来的大范围盲区现象需要引起末敏弹设计者的重视。对此，本文开展了大范围盲区现象的成因分析与对策研究，并得出如下结论：

1)大范围盲区现象的成因是离散标准化极角φ0(n)出现周期性地重复或小幅递进。

2)出现大范围盲区现象情况1，即扫描点集合形状为若干线段的条件是，采样时间间隔满足(11)式。

3)出现大范围盲区现象情况2，即扫描点集合形状为“叶子”(无伞无翼末敏弹)或“半片叶子”(有伞或有翼末敏弹)的条件是采样时间间隔满足(26)式(无伞无翼末敏弹)或(28)式(有伞或有翼末敏弹)。

4)工程实际中，转速波动较小时，仍然会出现显著的大范围盲区现象。

5)采用等时间间隔采样模式时，减小采样时间间隔、增加敏感器视场角可减小大范围盲区现象所引起的盲区半径，但这需要较高的硬件性能，提升了硬件成本，并可能引入噪声、降低目标定位精度。

6)采用随机采样模式，可在保持末敏弹现有硬件方案的前提下，有效降低大范围盲区现象所引起的盲区半径，具有较强的实用性。