基于工作空间的踝关节康复广义球面并联机器人运动学参数优化

刘秀莹 张建军 刘承磊 牛建业 戚开诚 郭士杰

1.河北工业大学机械工程学院，天津，3001302.河北省机器人感知与人机融合重点实验室，天津，300130

0 引言

踝关节为人体重要关节之一，调查显示每天踝关节损伤病人占医院急诊科所有入院人数的7%～10%[1]。踝关节损伤后较难进行及时、规范的康复治疗，康复训练时长也难保证，因此，研发性能优良的踝关节康复机器人既可使患者得到规范、充分的康复训练，又可缓解我国患者多、康复医师少的问题。

国内外学者对踝关节康复机器人进行了大量研究。SAGLIA等[2]提出了多种少自由度并联机构，可实现踝关节的背伸跖屈、内外翻运动。JAMWAL等[3]提出了一种用于脚踝辅助康复训练的三自由度柔性并联机构。ZHANG等[4]提出了一种顺应性踝关节康复机器人。MA等[5]提出了具有柔性机构的康复机器人。姚立纲等[6]提出了一种混联式踝关节康复装置，并基于章动原理对康复运动进行轨迹规划，满足踝关节康复运动的安全性需求。戚开诚等[7]采用并联机构3-UrPS作为两足步行器的腿部机构，并对其工作空间进行了分析。俞志伟等[8]基于踝关节简化成虎克铰的等效模型设计了一种新型的双足机器人，并通过优化运动学参数使其在小功率驱动元件下运动性能良好。文献[9-12]以球为模型分别设计了3-RRR、3-SPS/S、3-RRRPP、2-UPS/RRR机构，并用于踝关节康复训练。文献[13-14]基于空间RR串联等效模型模拟了关节轴线交错的运动，并将其应用于踝关节康复机构上。上述研究工作推动了机器人的技术进步，改善了踝关节康复机器人的性能，然而，现有踝关节康复机器人多采用并联机构，并普遍将踝关节运动等效为转动轴线汇交于一点的球面副，使得康复机器人与踝关节的真实运动存在差异，造成人机运动不协调，机器人对人体产生额外非运动方向作用力，易造成人体二次损伤。

本文根据人体踝关节解剖结构和运动特性，提出一种用于拟合踝关节运动的双球心广义球面并联机器人，对该机器人进行了逆运动学、工作空间的分析，并基于双球心的特点，采用先局部优化动球心、后整体优化动平台工作空间的方法，求出满足踝关节运动需求的运动学参数。

1 踝关节运动串联拟合模型

人体踝关节是主要的负重部位之一，它包括胫距关节和距下关节两个独立的关节，胫距关节由胫腓骨下端与距骨上端组成，距下关节由距骨下端与跟骨组成。人体踝关节解剖结构如图 1 所示，其关节轴线在三维空间内呈现倾斜状态[15-16]，且相互不垂直、不交叉、方向位置随其运动改变，踝关节围绕多个瞬时旋转中心运动[17]。

图1 人体踝关节实际解剖图

空间RR踝关节运动拟合模型(一个固定的转动副轴心线模拟胫距关节轴线，另一个转动副轴心线模拟距下关节轴线)不能充分拟合人体踝关节运动[18]，RR模型如图2a所示。本文提出的空间UR模型(虎克铰U，可视为两个转动副，其中一个转动副R1轴心线模拟胫距关节轴线，另一个转动副R2的作用是使R1轴心线运动，转动副R3轴心线模拟距下关节轴线)能更好地模拟踝关节运动轴线，它的模型如图 2b所示。

文献[18]中采用X-Y-Z欧拉角表示踝关节运动串联拟合模型末端的位姿。根据人体坐标系，原点为转轴中点，右腿Z轴由内向外为正。UR模型坐标系如图2c所示，惯性系{0}系的原点为胫骨中点，Z0轴与膝关节轴线平行，由内向外。内外旋坐标系{1}系的原点为胫骨中点，Z1轴沿下肢长轴，垂直脚底向上。背伸跖屈(胫距关节)坐标系{2}系的原点为胫骨中点，Z2轴沿胫距关节轴线，由内向外。内外翻(距下关节)坐标系{3}系的原点为距骨中点，Z3轴沿距下关节轴线，由舟骨指向跟骨。末端坐标系{4}系的原点在距骨正下方的脚面上，Z4轴与Z0轴同向。在初始位置为人体直立姿势时，各坐标系旋转变化矩阵的旋转角度如表 1 所示，其中{0}-{1}表示{0}系到{1}系的旋转变换矩阵。

(a)RR模型 (b)UR模型(c)UR模型坐标系

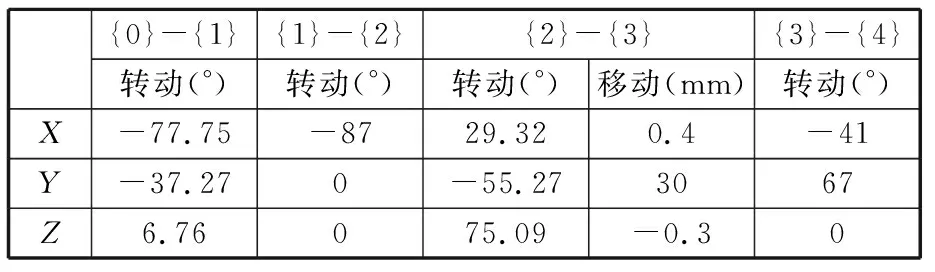
表1 踝关节运动串联拟合模型旋转变换参数表

踝关节运动过程中，Z1变化范围为-14.24°～32.76°，Z2变化范围为-25°～50°，Z3变化范围为42.09°～83.09°。从{4}系到{0}系旋转变换矩阵为

(1)

对踝关节运动串联拟合模型进行运动学分析，经旋转变换矩阵得到末端参考点的工作空间，将工作空间投影到人体解剖学的冠状面、矢状面和水平面中，得到{4}系原点的最大运动范围，该最大范围能够满足人体踝关节做背伸跖屈-30°～45°、内外翻-17°～22°、内外旋-25°～22°的运动，故模型建立正确。

2 广义球面并联机器人自由度分析

2.1 广义球面并联机器人描述

UR模型是针对踝关节结构拟合出的运动模型，不能作为康复机构本体，且人体距骨尺寸微小，串联机构电机无法安装。为满足UR串联模型运动特性，提高踝关节康复运动精度，采用一种双球心广义球面并联机器人实现踝关节康复运动，该机器人结构如图 3 所示。该机器人主要部分是一个广义球面并联机构，如图 4 所示，机构的定球心O和动球心O1分别匹配胫距关节与距下关节，且两球心间的距离满足距骨尺寸要求。机构由动平台、静平台和连接两平台的三条支链组成，其中支链一和支链三具有相同的结构，包含三根球面连杆和四个转动副，相对于定球心O呈对称分布；支链二包含四根球面连杆和五个转动副。三条支链与动平台相连的球面连杆的转动副铰接孔轴心线均通过动球心O1，剩余球面连杆的转动副铰接孔轴心线通过定球心O。在机器人运动过程中，动平台绕O1做球面转动，O1绕O做球面转动。支链一和支链三的球面连杆l1、l2、l8、l9与定平台组成以定球心为汇交中心的球面五杆闭环，当支链一和支链三的输入转角θ1和θ3确定时，就可以求得动球心的空间位置。

图3 踝关节康复广义球面并联机器人

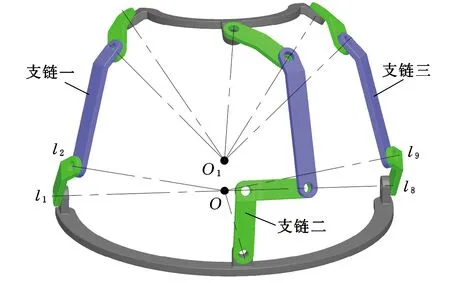
图4 广义球面并联机构

2.2 自由度分析

为了分析该机器人的运动性能，采用螺旋理论计算广义球面并联机构的自由度。支链一和支链二坐标系如图5所示，在该机构运动的任意位置，以定球心O为原点、OO1为Z0轴建立瞬时坐标系。定义Rij为第i条支链第j个转动副，其中R11、R12、R21、R22、R23、R31、R32轴心线过原点，R13、R14、R24、R25、R33、R34轴心线过Z0轴。

(a)支链一 (b)支链二

第一条支链运动螺旋系为

(2)

式中，l为OO1的长度；a0ij、b0ij、c0ij为与各转动副的方向和位置相关的量。

根据螺旋理论和线几何原理，转动副铰接孔轴心线不会出现空间三个力线矢共面汇交于一点、共面平行或共轴的情况，故支链一的四个螺旋线性无关。对式(2)求反螺旋，可得到支链一的约束螺旋系:

(3)

同理可得支链三的反螺旋系:

(4)

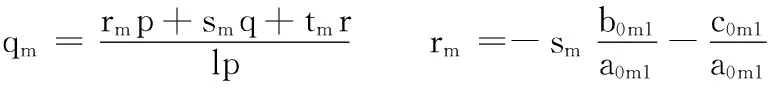
q=b0m4b0m3-b0m3b0m4r=c0m4b0m3-c0m3b0m4

tm=1m=1、3

第二条支链运动螺旋系为

(5)

对式(5)求反螺旋，得支链二的反螺旋系:

(6)

每条支链中都提供给动平台一个经过坐标系原点且平行于Z0轴的约束力，其中两个为虚约束，利用修正的G-K公式，可求得机构的自由度:

M=6×(12-13-1)+13+2-0=3

(7)

根据运动螺旋系与约束螺旋系互易积为零的关系，可以求出机构的运动螺旋和节距为

(8)

(9)

与一般有固定球心的三自由度球面并联机构相比，广义球面并联机构存在两个球心，动球心绕定球心转动，同时动平台绕动球心转动，没有固定的转动中心；广义球面并联机构动平台的运动螺旋系为一个三阶螺旋系，既包含节距为零的特殊螺旋(线矢量)，也包含节距不等于零的螺旋，故广义球面并联机器人能够从自由度上满足踝关节康复需求。

3 运动学分析

为了得到广义球面并联机器人动平台的位置，需要对广义球面并联机构进行逆运动学分析。建立机构运动学坐标系如图6所示，以定球心O为原点，OR21为x0轴，OR31为y0轴，垂直于定平台方向为z0轴,建立定坐标系{0}系；以O为原点，OO1为z1轴，初始位置y1平行于y0，x1轴方向由右手定则确定,建立中间坐标系{1}系；在动球心O1处，初始位置与定坐标系完全平行，建立动坐标系{2}系；(a1，b1，c1)表示O1点的坐标，(aij，bij，cij)表示Rij转动副中心点的坐标，ηij为各个球面连杆所对应的圆心角。

图6 广义球面并联机构坐标系简图

运动学逆解是已知广义球面并联机构动平台的位姿，求解输入转角。本文采取封闭矢量法进行运动学逆解的计算，并通过机构的几何关系和实际装配关系得到逆运动学的唯一解。在进行逆解运算时，用球面坐标表示机构动平台位置，采用欧拉角表示机构动平台姿态的方法来给定动平台的位姿参数。由定坐标系{0}系绕z轴转α，绕新的y轴转β，沿新的z轴移动固定距离l得到中间坐标系{1}系，再绕新的z轴转γ，绕y轴转φ，绕x轴转δ得到动坐标系{2}系。在中间坐标系{1}系下，R13、R33位置可以确定，后三个转角γ、φ、δ只有一个独立，此时机构能够运动的部分见图7。

图7 旋转变换角关系图

由{0}系到{1}系的旋转变换矩阵为

(10)

由{1}系到{2}系的旋转变换矩阵为

(11)

nz=cosγcosφ

oz=cosγsinφsinδ-sinγcosδ

az=cosγsinφcosδ+sinγsinδ

ny=sinγcosφ

oy=sinγsinφsinδ+cosγcosδ

ay=sinγsinφcosδ-cosγsinδ

nx=-sinφox=cosγsinδ

ax=cosφcosδ

由定坐标系{0}系到动坐标系{2}系的旋转变换矩阵为

(12)

d11=cosαcosβnz-sinαny+cosαsinβnx

d21=sinαcosβnz+cosαny+sinαsinβnx

d31=-sinβnz+cosβnx

d12=cosαcosβoz-sinαoy+cosαsinβox

d22=sinαcosβoz+cosαoy+sinαsinβox

d32=-sinβoz+cosβox

d13=cosαcosβax-sinαay+cosαsinβax

d23=sinαcosβax+cosαay+sinαsinβax

d33=-sinβax+cosβax

由式(12)旋转变换矩阵T的位置矢量可知,动坐标系的位置坐标只与α、β有关，而动坐标系的姿态与α、β、γ、φ、δ五个旋转变换角有关。

当给定机构动平台原点位置坐标时，即在中间坐标系{1}系下，通过封闭矢量法可得R12的位置：

(13)

式中，lij为第i条支链第j个转动副轴心线的长度。

使用数学计算软件MATLAB R2014a的solve函数解方程组可得R12坐标矢量，其中c12为

(14)

f=a1b11-a11b1g=a1a11+b1b11

h=(l11lcosη12-gcosη11)

e=f2+(l11c1)2-(l11l)2n+m

由上可知，支链一的输入转角

(15)

式中，li(i=1，2，…，10)为球面连杆的长度。

同理可得，支链三的输入转角

(16)

由θ1和θ3的表达式可知支链一和支链三的输入转角只与α、β有关，即支链一和支链三为机构的位置支链。又因为R12R13O1O在同一平面上，故可求出R13、R33的坐标矢量。

通过旋转变换矩阵T1可得在中间坐标系{1}下R131、R331的坐标矢量，为求解后三个转角γ、φ、δ的关系做铺垫。当给定位置支链某一输入转角时，部分能动机构如图 7 所示，由位置解关系式可得到后三个转角γ、φ、δ的关系：

(17)

此时动平台绕O1做一自由度的转动，设在某一瞬时绕W轴转动θ角度，即

(18)

(19)

动平台上支链二转动副中心点在动坐标系下的坐标为

R′25=(l25sinη26，0，l25cosη26)

(20)

R25=TR′25

(21)

通过l24、η25、η24、l、l23、面OO1R24R23的法向量和η21、η22、l22三组方程组可求得R24、R23、R22坐标矢量，其中c22为

(22)

q0=a21b23-a23b21s=a21a23+b21b23

w=l21l23cosη21cosη22

由此可知，支链二的输入转角为

(23)

根据式(23)可知，θ2与α、β、γ、φ、δ五个旋转变换角有关，故称支链二为机构的姿态支链。

支链一和支链三决定动平台的位置，支链一、支链二、支链三共同决定动平台姿态，广义球面并联机器人存在位置和姿态部分解耦特性。

4 广义球面并联机器人工作空间分析

踝关节主要通过关节运动练习进行康复，所以对广义球面并联机器人工作空间进行分析是必要的。本文采用数值搜索法求解可达工作空间，并将工作空间分析结果作为后续运动学参数优化的依据。

4.1 工作空间的约束条件

本文主要考虑广义球面并联机器人驱动转动副的转动范围，理论上驱动转角可在[0，2π]取值，但由于实际装配情况，选取驱动转角θi范围为[0，π]，且驱动转角的取值为实数。

4.2 工作空间算例

本文求解广义球面并联机器人工作空间的MATLAB程序流程图见图8。

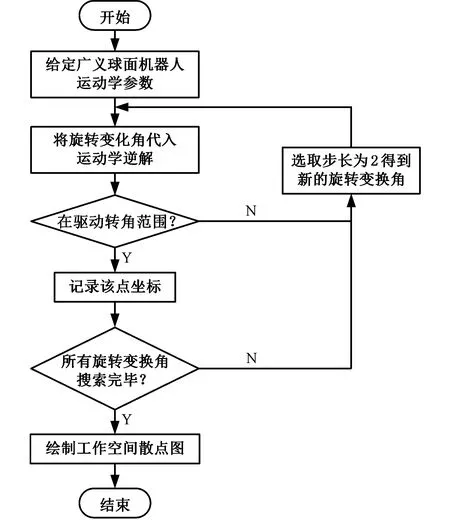
图8 工作空间求解流程图

选取动球心和动平台中心的点为输出散点，得到动球心和动平台工作空间的可视化散点图，分别如图9和图10所示。

图9 动球心工作空间

图10 动平台工作空间

依据初始运动学参数，从散点图上可以看出，广义球面并联机器人的工作空间在各个基准面上的投影都具有一定的对称性，且内部没有空洞，表明在有效的工作空间内机器人的运动性能良好。然而，该尺寸下的工作空间并没有满足踝关节运动串联拟合模型的工作空间，故需要对该机器人的运动学参数进行优化。

5 广义球面并联机器人运动学参数优化

以广义球面并联机器人动球心和动平台的工作空间与踝关节运动串联拟合模型的 U 和 UR 工作空间的匹配度为目标函数，以运动学参数为设计变量，在球面五杆闭环运动学条件和仿生条件等约束下，通过MATLAB遗传算法(GA)工具箱进行优化计算。

5.1 设计变量

据GB/T10000—1988《中国成年人人体尺寸》中人体尺寸百分位数取50% 中数据[19]，25～35岁的男性足长223～271 mm、足宽86～106 mm。定平台半径取足长的一半130 mm。动平台底板长300 mm、宽150 mm，动平台转动副中心线长173 mm，为了方便脚进入广义球面并联机器人，三条支链采取90°均布。依据装配关系可知，所有的转动副中心线长度都是确定的。

由上述分析可知，影响该机器人工作空间的运动学参数为η11=η31=A1、η12=η32=A2、η21=η22=A3、η23=A4、η24=η13=η33=A5、η13=η34=η25=A6、η26=η14=η34=A7。

5.2 目标函数

广义球面并联机器人与人体理论工作空间的匹配程度越高，对踝关节康复的效果越好，二次损伤越小，人机协调性越好。对该机器人的局部和整体工作空间进行优化，以踝关节运动拟合模型{3}系和{4}系原点工作空间与该机器人的动球心和动平台工作空间散点的坐标差值的平方和最小为目标建立目标函数：

(24)

式中，XPi、YPi、ZPi为踝关节运动拟合模型理想坐标值；xti、yti、zti为广义球面并联机器人的工作空间点坐标经过绕定坐标系x0、y0各旋转90°得到的值；i为工作空间的散点数目。

5.3 约束条件

(1)球面五杆闭环能组成又能运动的条件为

(2)动平台理想转角约束如表2所示。

表2 约束转角

(3)连杆不干涉条件：两回转副中心点的距离不小于连杆宽度。

(4)仿生条件：中医上称外踝尖到足底为三寸(99.9 mm)，设置动平台定平台间的距离为100～180 mm。人体胫距关节轴线和距下关节轴线间距为30 mm[20]，故球心距为30 mm。

综上，设计变量的约束范围设置分别为

Amax=[0° 45° 0° 0° 90° 0° 0°]T

Amin=[90° 90° 60° 90° 180° 30° 45°]T

5.4 运动学参数优化算例

通过MATLAB软件中的GA算法工具箱对广义球面并联机器人运动学参数进行求解，工具箱的优化参数设置如表3所示。

表3 GA算法的优化参数

求解广义球面并联机器人运动学参数的GA程序流程图见图11。

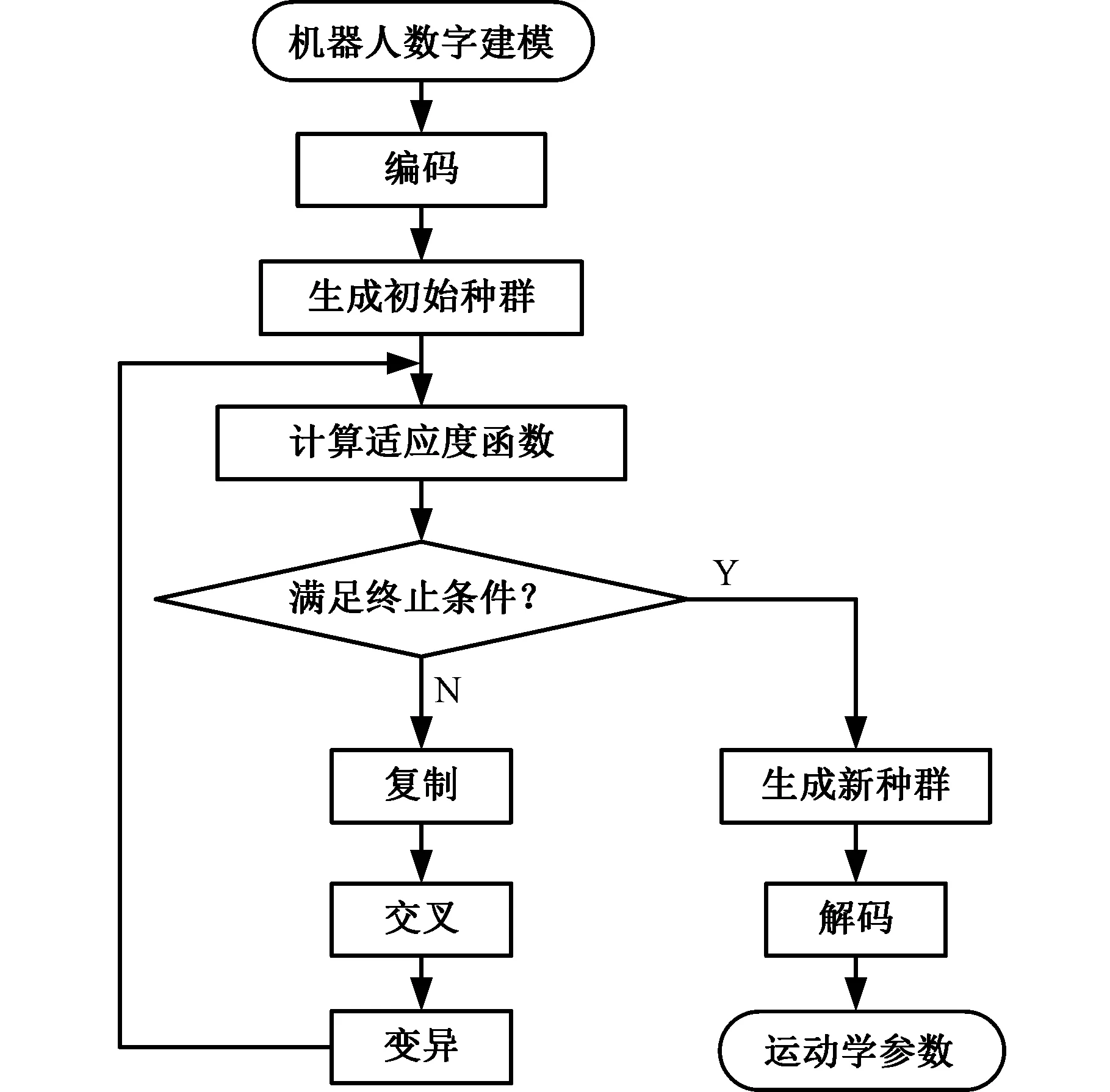
图11 GA程序流程图

利用GA算法求解得到的进化曲线见图12，进化代数在26和80左右，最优适应度函数值和平均适应度函数值逐渐接近，表明适应度函数已经收敛到最优解，即此时广义球面并联机器人工作空间与踝关节运动串联拟合模型工作空间最为接近。

(a)球面五杆闭环运动学参数优化曲线

将各运动学参数取整，如表4所示。使用优化后的运动学参数，在MATLAB中编程绘制出广义球面并联机器人动球心O1和动平台O2工作空间散点图，与踝关节运动串联拟合模型的{3}系和{4}系最大工作空间作对比，如图 13 所示，可以看出优化后的工作空间完全满足踝关节工作空间，而且优化后的工作空间对称，内部没有空洞，表明在工作空间内部无球面连杆干涉现象的发生，因此广义球面并联机器人具有良好的工作能力，更符合工程实际。

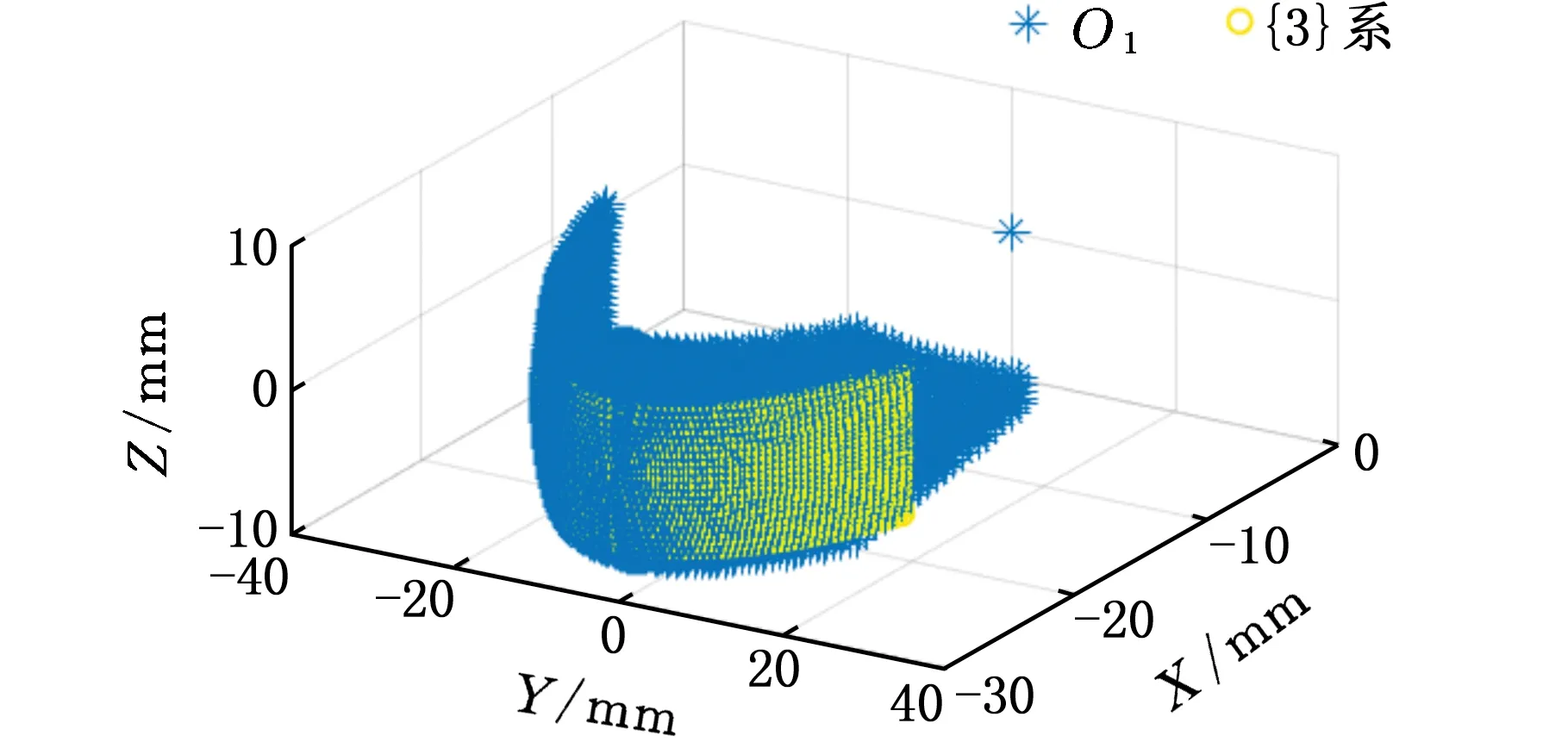
(a){3}系与动球心工作空间对比图

表4 优化后的机器人运动学参数

依据“散点图”区域内“散点”数量，工作空间大小的计算公式[21]可以表示为

V=iΔαΔβΔγ

(25)

式中，Δα、Δβ、Δγ为变量步长。

为了使广义球面并联机器人的空间完全包容踝关节运动串联拟合模型空间，将对比结果量化，评价机器人可达空间有效尺度域(无奇异、性能良好的可达空间)的相对大小，有效工作空间比ξ[22]的计算公式如下：

ξ=Vt/Vw

(26)

式中，Vt为踝关节运动串联拟合模型空间体积；Vw为广义球面并联机器人的工作空间体积。

{3}系与动球心的有效工作空间比ξ1为

{4}系与动平台的有效工作空间比ξ2为

有效工作空间比的结果表明，踝关节运动串联拟合模型的工作空间与机器人的可达工作空间接近，表明优化后的机器人能够满足踝关节运动需求，且机器人的运动学参数合理。

6 结论

(1)通过对人体踝关节解剖结构和运动特点进行分析，基于 RR 模型提出 UR 模型，建立了 UR 踝关节运动串联拟合模型的运动学正解模型，得到了踝关节的运动范围。

(2)用球面坐标表示动平台位置、欧拉角表示机构动平台姿态的方法，确定了动平台的位姿参数，采用封闭矢量法对机器人进行了逆运动学求解。根据逆运动学得到了广义球面并联机器人的运动范围和工作空间的约束条件，并通过MATLAB编程对其进行了工作空间的分析。

(3)以踝关节运动串联拟合模型与广义球面并联机器人的工作空间点的匹配程度为优化目标，通过遗传算法对该机器人的运动学参数进行了优化，得到了符合人体踝关节工作空间的运动学参数。将广义球面并联机器人与踝关节运动串联拟合模型的工作空间散点图进行对比，并求得有效工作空间比分别为0.79和0.86，验证了优化结果的合理性，能够满足人体踝关节的工作空间。