基于改进响应面法的电缆-碳纤维增强复合材料集成构件电缆埋置位置优化
杨 旭 周德俭, 庄功伟 宋 微 刘潇龙 佘雨来
1.西安电子科技大学机电工程学院,西安,7100712.桂林电子科技大学机电工程学院,桂林,541004 3.中国电子科技集团公司第十研究所,成都,610036
0 引言
随着无人机机载电子设备和电缆数量的不断增加,电缆布线空间变得越来越拥挤。碳纤维增强复合材料(CFRP)具有重量轻、强度高、稳定性好等特点,已被广泛应用于航空、航天和汽车等领域[1-2]。本研究将多根电缆埋入到CFRP基体中形成集成构件,既可以节省宝贵的布线空间,又能很好地保护和定位电缆,具有很好的应用前景。
现阶段集成构件已经成为研究热点,部分学者已对复合材料集成构件的可行性和应用效果进行了研究。LING等[3]将光纤埋入到复合材料结构中形成集成构件,已得到应用并取得了很好的效果;ARELLANO等[4]和TORRES等[5]使用有限元法(FEM)研究了传感器嵌入复合材料后对构件力学性能的影响,结果表明这个影响并不显著,证明了在复合材料中嵌入元器件的可行性。电缆的埋置位置是电缆-CFRP集成构件的重要参数,但目前综合考虑力学性能、电磁兼容性能和制造约束条件的电缆埋置位置优化的研究还未见报道。响应面法(RSM)适用于统计建模和参数优化问题,近年来在机械工程和复合材料等领域得到了广泛应用。学者们使用RSM对多因素交互作用下中部槽磨损问题[6]、塑制汽车离合器总泵的上下泵体在旋转摩擦焊接工艺中的焊接参数[7]和高性能纳米复合材料的参数优化问题[8]进行了研究,都取得了很好的效果。但现有的响应面法在求解包含高阶项的非线性问题时,可能会存在预测值与实际验证值吻合情况不佳的情况。
本文针对电缆-CFRP集成构件中电缆埋置位置的优化问题,提出了一种改进响应面法,并在此基础上提出了一种求解电缆埋置位置参数优化问题的方法。
1 建立问题模型
在建立问题模型之前,使用模压工艺制造出了一批电缆-CFRP集成构件的样件,如图1所示,可见,将电缆埋入CFRP基体后,会在电缆周围形成一个楔形的树脂富集区。一方面,本研究根据样件富集区的大小比例来建立后续的几何模型、有限元模型和电缆串扰仿真模型,从而保证计算精度;另一方面,通过前期的加工过程发现一些约束条件,它们将作为本研究中优化问题的约束条件,保证研究结果的可加工性。

图1 电缆-CFRP集成构件的样件
本研究中电缆-CFRP集成构件的结构示意图见图2,其长度、宽度和厚度尺寸分别为400 mm、160 mm和14 mm,顶面距离铝制接地板7 cm,内埋有三根平行布置的电缆。设电缆1和电缆2中心线的间距为D1,电缆2和电缆3中心线的间距为D2,电缆中心线距离接地板的距离为H。这三根电缆处于工作状态时,均传输pulse型信号,信号的延迟时间和峰值保持时间为0.003 μs,上升沿时间和下降沿时间为0.001 μs,各电缆的信号周期、幅度、内径和外径如表1所示。
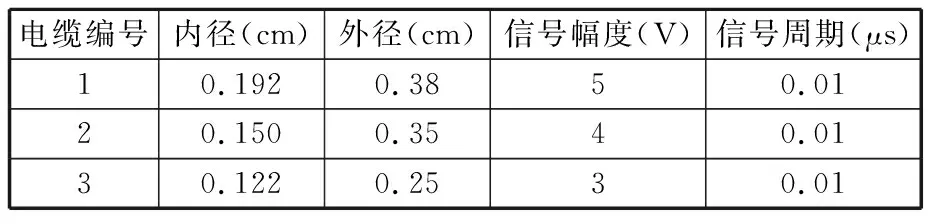
表1 电缆参数
定义弯曲载荷工况1如下:以图2所示的集成构件底面的2个支撑线处为支撑,支撑跨距为320 mm;在构件顶面的加载线上施加100 N的弯曲载荷,加载线位于顶面的中间位置。集成构件几何模型的正面视图见图3。

图2 电缆-CFRP集成构件的结构示意图

图3 集成构件几何模型的正面视图
由于集成构件受到弯曲载荷时其内埋电缆也会产生应力,为了避免电缆的过度变形和损坏[9],必须使电缆的最大应力小于最大允许值;另外,电缆近端串扰过大会对敏感设备造成干扰[10-11]。综合考虑系统整体设计的需求和制造工艺约束,给出本研究优化问题的约束条件如下。
约束1:所有电缆的近端串扰电压均不能超过其所传输信号幅度的4%。
约束2:电缆的应力最大值不能超过4 MPa。
约束3:1.5 cm≤D1≤4.5 cm;2 cm≤D2≤6 cm;1 cm≤H≤1.6 cm;D1+D2≤7.5 cm。
本研究电缆埋置位置优化问题的目标是:集成构件处于工况1时,在满足以上所有约束的前提下,所有电缆的近端串扰电压都尽可能小。
2 分析方法
2.1 基于FEM的应力计算
本研究选用型号为T300/5208的各向异性碳纤维增强树脂基复合材料作为集成构件的基体材料,其材料属性如表2所示。

表2 T300/5208的材料属性
电缆内芯、绝缘层和树脂富集区的材料属性如表3所示。
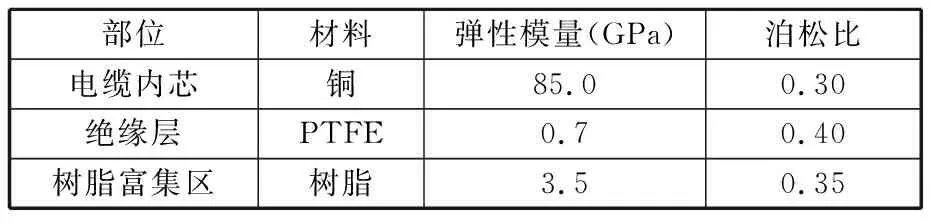
表3 电缆内芯、绝缘层和树脂富集区的材料属性
使用ANSYS有限元分析软件计算在工况1下集成构件的应力分布,如图2所示,建立集成构件的几何模型后,以其底面的2个支撑线处为支撑,在顶面的加载线上施加100 N的弯曲载荷,支撑跨距为320 mm,然后划分网格,基于FEM计算得到应力分布。
2.2 基于多导体传输线法的电缆串扰电压计算
本研究基于多导体传输线法,使用CST电磁仿真软件建立电缆和接地板的几何模型,然后采用集总法和模式法两种方法提取出电缆的分布参数,生成等效电路模型并设置激励信号和负载,计算出接收线上的串扰电压[12-14]。以电缆2为发射线,电缆1和电缆3为接收线时的等效电路模型如图4所示。

图4 等效电路模型
激励源设置在发射线上,每次仿真只设置一个激励源,然后基于叠加原理,计算出所有激励源同时工作时每根电缆的近端串扰电压的最大值。叠加原理的表达式如下:
(1)
式中,U1为电缆1上的总串扰电压;U1k为电缆k对电缆1产生的串扰电压。
2.3 RSM试验设计与分析方法
本研究使用Design-Expert.v8.0.6.1软件进行响应面分析和优化,在完成了试验方案的设计和试验结果数据的输入之后,先尝试使用一阶模型进行拟合,拟合公式如下:
(2)
其中,y表示响应,x表示设计变量,e表示拟合误差。如果一阶拟合的拟合程度不能满足要求,则采用二阶模型进行拟合,其表达式如下:
(3)
得到各因变量与响应之间的数学表达式之后,基于方差分析对模型的质量进行评价,以验证模型的正确性[8,15]。
3 电缆埋入位置的优化
3.1 优化方法
本研究提出一种求解电缆埋置位置参数优化问题的方法,其流程如图5所示。具体步骤如下:首先,建立优化问题的ANSYS仿真模型和CST电磁兼容仿真模型;然后,建立RSM模型和基于Box-Behnken design(BBD)的优化模型,得到初步的埋置位置参数后,将预测值与实际值进行对比,判断计算误差是否满足要求,若是,则优化完成,否则使用改进RSM法进一步优化;得到最优解后,计算预测误差和约束条件是否满足,如果不满足,根据误差分布,在计算时对约束条件进行适当的“修正”以抵消建模误差,直至优化结果满足所有要求。
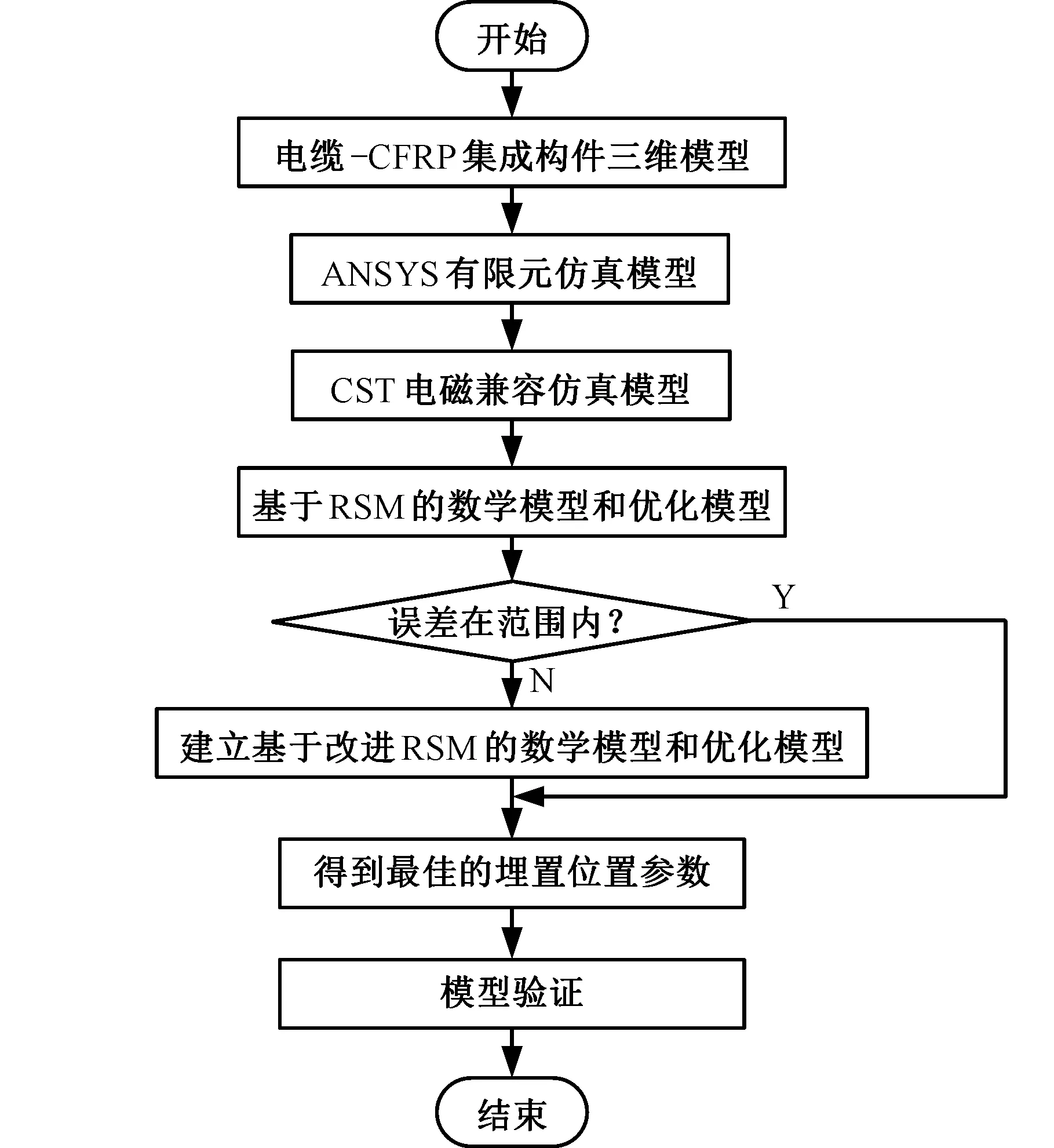
图5 优化方法的流程图
3.2 基于RSM的优化
定义电缆间距D1和D2为设计变量A和B;定义电缆中心与接地板间的距离H为设计变量C;电缆1、电缆2、电缆3的近端串扰电压最大值U1、U2、U3和电缆的应力最大值σ1为拟合模型中的4个响应。采用BBD针对这3个设计变量和4个响应设计了17组试验,包含5组中心重复试验,试验方案和试验结果如表4所示。
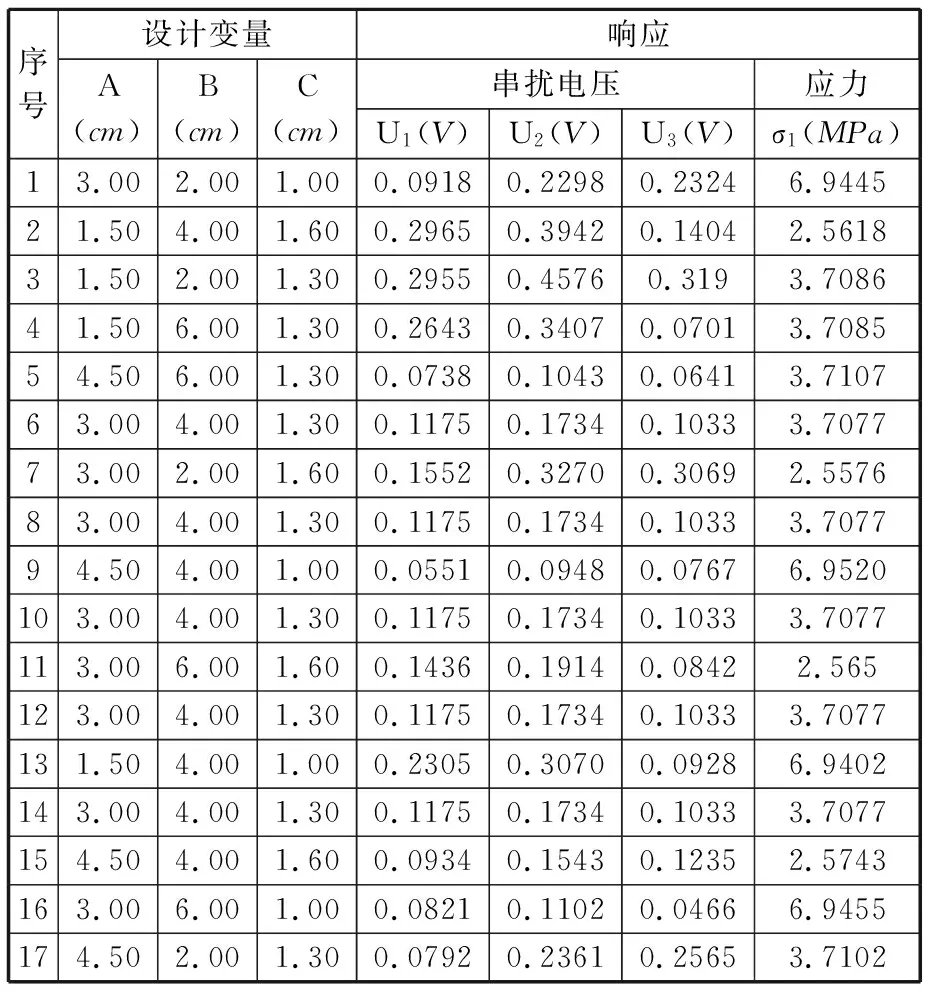
表4 试验方案和试验结果
计算出初步的拟合模型后,使用AB2、AC2等高阶项对拟合模型进行修正,并去除对响应影响不大的因素项,得到各响应模型的方差分析结果,如表5所示。使用F检验来判断模型的显著性[8],回归平方和(F值)的值越大,说明模型越显著;失效概率的值越小,说明拟合模型失效的概率越小,模型越有效。

表5 各响应模型的方差分析结果
如表5所示,本研究中所有响应的F值都很大,失效概率均小于0.05,且失拟项的数值都很小,这说明模型的拟合效果较好,建立的拟合模型是显著的和正确的。
通过三维响应值曲面图来分析各因素对响应的影响关系。由于篇幅原因,只列出其中三个三维响应值曲面图,见图6。由图6a可知,D1对U1的影响大于D2;由图6b可知,D2对U3的影响大于H,当D2和H的取值分别在2.0~2.5 cm和1.3~1.6 cm区间时,这两个因素之间有较强的相互作用;由图6c可知,H对σ1的影响大于D2。结合其余所有三维响应值曲面图可知:所有电缆的近端串扰电压均随着D1和D2的增大而减小,随着H的增大而增大;电缆的最大应力σ1随着D1和D2的增大而增大,随着H的增大而减小。

(a)U1相对于D1和D2
应用RSM进行基于BBD的优化,以获得初步的电缆布置优化方案。由前面的分析可知,目标函数G的表达式如下:
(4)
其中,ω1、ω2、ω3都取1。约束条件的数学表达式如下:
(5)
计算得到各响应的预测值和参数组合后,将这些参数代入仿真模型中进行计算,得到的优化结果如表6所示,可见,有三个响应的实际值与预测值的误差大于5%,且σ1没有满足约束条件,说明使用传统的RSM进行优化无法满足精度要求和部分约束条件。

表6 优化结果
3.3 基于改进RSM的优化
本研究提出基于贪心策略和切比雪夫多项式采样策略的改进响应面法,以提高拟合模型的精度和预测性能。对于一个连续的拟合函数f(x),其表达式可用n阶多项式pn(x)来无限逼近,由于切比雪夫级数与最佳逼近函数十分相近[16],故f(x)近似表达如下:
(6)
i=0,1,…,n
其中,Ci(x)为切比雪夫多项式,fi为常数项系数,可用式(7)近似表示[16]:
(7)
针对预测效果不理想的响应,基于前面的RSM分析,找出影响最大的设计变量x,设其最小值为x1,最大值为x2,引入贪心因子δ1和δ2,缩减采样点的区间,其采样点集合X0的表达式为
(8)
x′1=x1+δ1(x2-x1)
x′2=x2-δ2(x2-x1)
如果满足下面的式(9)和式(10),则说明其取值范围往左缩小能够更接近优化目标值的区间,应令δ1小于δ2;同理,如果满足式(11)和式(12),应令δ1大于δ2;对于其他情况,可令δ1和δ2取相近值;为了避免陷入局部最优,δ1和δ2的取值范围为(0,0.3)。
(9)
(10)
(11)
(12)

在X0的基础上,根据切比雪夫多项式零点得出的采样点集合X1为
(13)
在X1的基础上,为了提高全局搜索的能力,引入贪心补偿项Δ1和Δ2,确保前一步得到的x的最优值xr不在采样区间的边缘,以免陷入局部最优,得到X2的表达式如下:
(14)
xr-(x″1+Δ1)<0.25(x″2+Δ2-x″1-Δ1)
(x″2+Δ2)-xr<0.25(x″2+Δ2-x″1-Δ1)
根据提出的改进响应面法,本研究对设计变量A的采样策略进行改进,最终计算得到采样点空间A2为(3.1,3.6,4.1);其余设计变量的采样点不变,计算得到各响应模型的表达式如下:
U1=0.243 72-0.130 11A-0.048 216B+
0.215 19C+0.011 05AB-0.036 133AC+0.017 768A2+
0.005 2131B2-0.001 232 5AB2
(15)
U2=0.671 04-0.217 52A-0.178 91B+0.304 01C+
0.019 777AB-0.041 567AC-0.007 304 17BC+
0.027 343A2+0.018 543B2-0.002 163 75AB2
(16)
U3=0.830 08-0.236 04A-0.226 17B+0.142 42C+
0.035 082AB-0.013 95BC+0.028 965A2+
0.015 624B2-0.004 26A2B
(17)
σ1=32.872 35+0.002 15A-0.004 056 25B-
37.560 01C+0.003 75BC+11.629 03C2
(18)
得到的优化结果如表7所示,可见,改进后所有响应的实际值与预测值的平均误差仅为3.37%,另外,改进后各响应模型的F值、Adj R-Squared和Pred R-Squared均比改进前有所提高,这说明改进后的各响应模型的质量得到了提高。但是,改进后σ1的实际值仍比预测值稍大,导致优化结果未能满足所有约束条件。
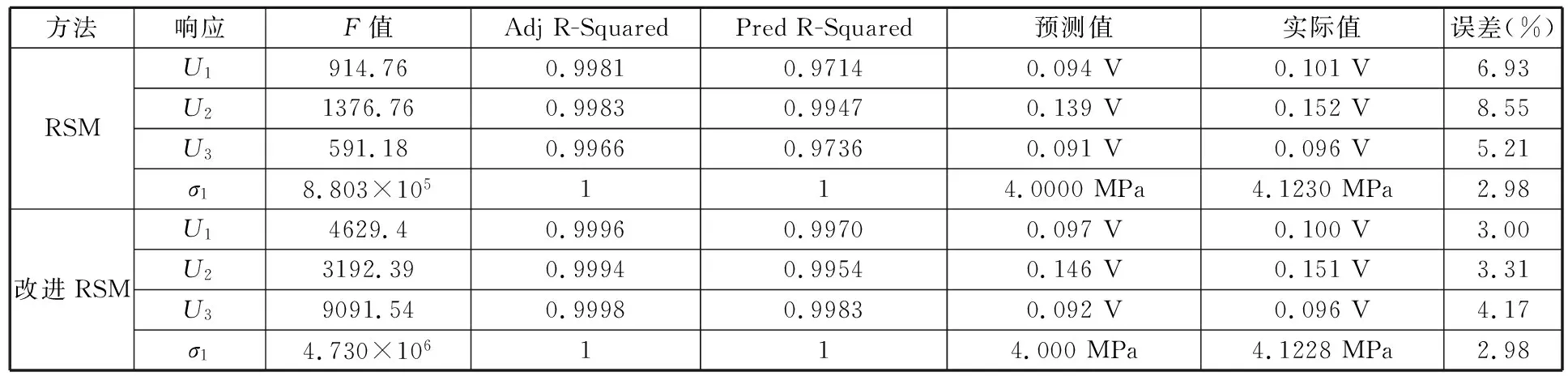
表7 改进后的优化结果
由于电缆最大应力的实际值比预测值稍大,为了抵消误差,在优化时将应力约束条件“修正”为:σ1≤3.88 MPa,其余约束条件不变。最终得到的最优设计变量是:D1=3.39 cm,D2=4.11 cm,H=1.28 cm。得到的电缆最大应力的位置如图7所示,优化结果如表8所示。可见所有响应的实际值与预测值间的平均误差仅为3%,且优化结果满足所有的约束条件。

图7 电缆最大应力的位置
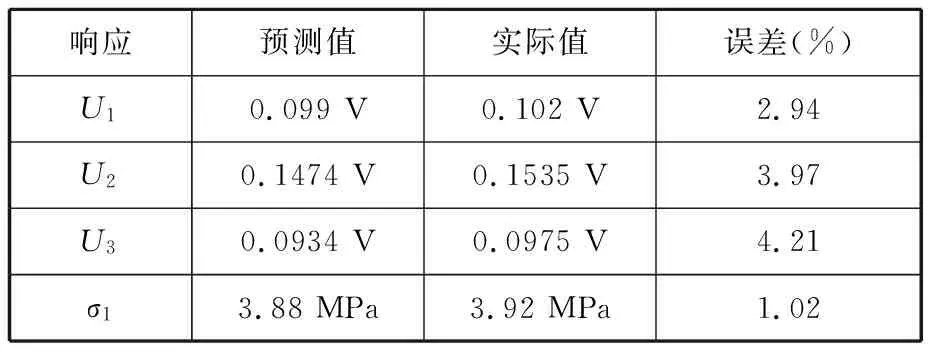
表8 满足约束条件的优化结果
3.4 预埋电缆对CFRP基体力学性能的影响
预埋电缆前后CFRP基体的弯曲应力分布如图8所示。可见埋入电缆后,CFRP基体的应力分布变化不大,且埋入电缆前后CFRP基体的最大应力分别为2.154 MPa和2.168 MPa,可见,预埋电缆对CFRP基体的力学性能影响很小。

(a)预埋电缆前
为了验证使用仿真方法对电缆-CFRP集成构件进行应力应变分析的有效性,首先,根据本研究优化得到的最优设计变量(D1=3.39 cm,D2=4.11 cm,H=1.28 cm)加工得到电缆-CFRP集成构件的实物;然后,使用应变仪对其进行实验测量,如图9a所示。实验时施加的载荷和约束条件与前面有限元仿真中的保持一致(即前面定义的弯曲工况1)。
由于电缆被埋置在构件内部,故无法直接测量电缆的应力应变。CFRP基体应力应变最大的部位下面刚好是支撑底座,也不适合测量。由图8b可见,集成构件底面的中心部位的应变较大且容易测量,因此,本研究在此处粘贴三向应变花来测量其应变(图9),并与仿真结果进行对比。测量得到该部位在0°、45°和90°方向的应变分别为-0.95×10-6、-17.05×10-6和46.05×10-6,通过三向应变花的应变计算公式可得应变花粘贴位置的最大和最小主应变的值分别为6.86×10-5和-2.35×10-5。有限元仿真得到的电缆-CFRP集成构件底面上的应变分布如图10所示,仿真得到的最大和最小主应变的值分别为7.40×10-5和-2.25×10-5。

1.实验样件 2.支撑底座 3.加载件 4.信号线 5.应变仪 6.测量界面

(a)最大主应变分布
计算得到应变花粘贴位置的最大和最小主应变的仿真结果与实验结果的误差分别为7.9%和4.3%,仿真结果与实验结果具有很高的吻合度,实验结果验证了仿真分析结果的准确性,故采用仿真方法对电缆-CFRP集成构件进行应力应变分析是有效的。造成仿真结果与实验测试结果之间误差的原因可能是样件加工时由工艺因素带来的制造误差和仿真模型中树脂区的建模误差。
4 结论
(1)电缆间距和电缆与接地板之间的距离对电缆间串扰和电缆上的最大应力都有重要影响,且这些因素之间存在一定的相互作用。
(2)本文提出了基于贪心策略和切比雪夫多项式采样策略的改进响应面法,与传统响应面法相比,使用提出的改进响应面法计算得到的拟合模型,其显著性、拟合度和预测效果都有较大的提高,表明该方法更适合求解包含高阶项的非线性问题。
(3)优化结果满足所有约束条件,所有指标的预测值与实际值的平均误差仅为3%。最优参数组合为:D1=3.39 cm,D2=4.11 cm,H=1.28 cm。结果表明,本文提出的基于改进RSM的优化方法是非常有效的,可以预测高质量的优化结果。
(4)使用最优埋置参数组合得到的集成构件,埋置电缆对CFRP基体力学性能的影响很小,说明使用所提方法设计的电缆-CFRP集成构件应用于工程实践是安全可靠的。

