人机协同控制的车道保持辅助系统安全性能研究

隋 新 刘春阳 詹 坤 王张飞 张毅晖

1.河南科技大学机电工程学院,洛阳,471003 2.机械装备先进制造河南省协同创新中心,洛阳,471003 3.河南省机械设计及传动系统重点实验室,洛阳,471003

0 引言

车道保持辅助(lane keeping assist，LKA)系统是一种高级驾驶辅助系统，主要用于防止驾驶员因分心、疲劳驾驶导致车辆偏离出车道线[1]。近年来，随着车道偏离预警技术的逐渐成熟，国内外越来越多的研究者聚焦于车道保持辅助系统研究，取得了丰富的成果，例如PID算法[2]、人工势场法[3]、模型预测控制算法[4]等。文献[5-7]建立了驾驶员模型、预瞄模型以及改进模型，通过建立车辆运动学和动力学模型，对车道保持控制算法进行研究，在控制性能上获得较好效果，但人机协同控制策略问题考虑较少。文献[8]从客车车道保持辅助系统实现的角度阐述了两种改进的模型预测控制算法，并从可行性和成本效益方面对两种方法进行定性对比，评述其优缺点。文献[9-11]充分考虑驾驶员特性，在横向控制算法基础上，建立远近视角驾驶员模型和车道偏离决策模型等，有效增强了人机合作程度，而对控制系统的激活/退出安全策略研究较少，难以保证驾驶员的绝对控制权。文献[12]将系统感知与鲁棒控制相结合，使驾驶员与LKA系统能够成功地共享控制权，提高了驾驶员与汽车之间的自动化理解，减少或避免了冲突，作者提到其LKA系统没有考虑车速变化，共享控制的鲁棒性还有待提高。文献[13]提出一种新车道保持辅助系统的共享控制方案，通过调整位移间隔来实现共享控制，并仿真了两种典型的工况。文献[14]基于电子助力转向器设计了一种车道保持辅助系统，并综合考虑车道线置信度、跨道时间、驾驶员状态等信息，提出一种车道保持辅助系统介入和退出策略，该策略有效提高了系统的安全性和舒适性，但文中模型参数较多,系统结构较复杂，调试困难。

针对以上问题，本文综合考虑人-车-路信息，设计了一种基于人机协同控制的车道保持辅助系统。采用最优线性二次型调节器(linear quadratic regulator，LQR)和PID控制算法，可以得到车道保持助力扭矩；通过横向距离误差、质心侧偏角误差和车速等判断车辆偏离状态，并联合助力扭矩和驾驶员实际扭矩实现车道保持人机协同控制；基于驾驶员实际扭矩、转向灯信号、车轮越线距离和车道线置信度等，提出一种安全退出策略，提高了人机共驾的安全性。

1 车辆动力学建模分析

车辆偏离车道线的运动主要是横向运动，故本文忽略车辆纵向动力学特性，重点考虑车辆横向动力学特性。如图1所示，建立简化的二自由度车辆动力学模型[15]，分析车辆轮胎及相关部件的受力情况。车辆动力学方程中各参数及其含义见表1。

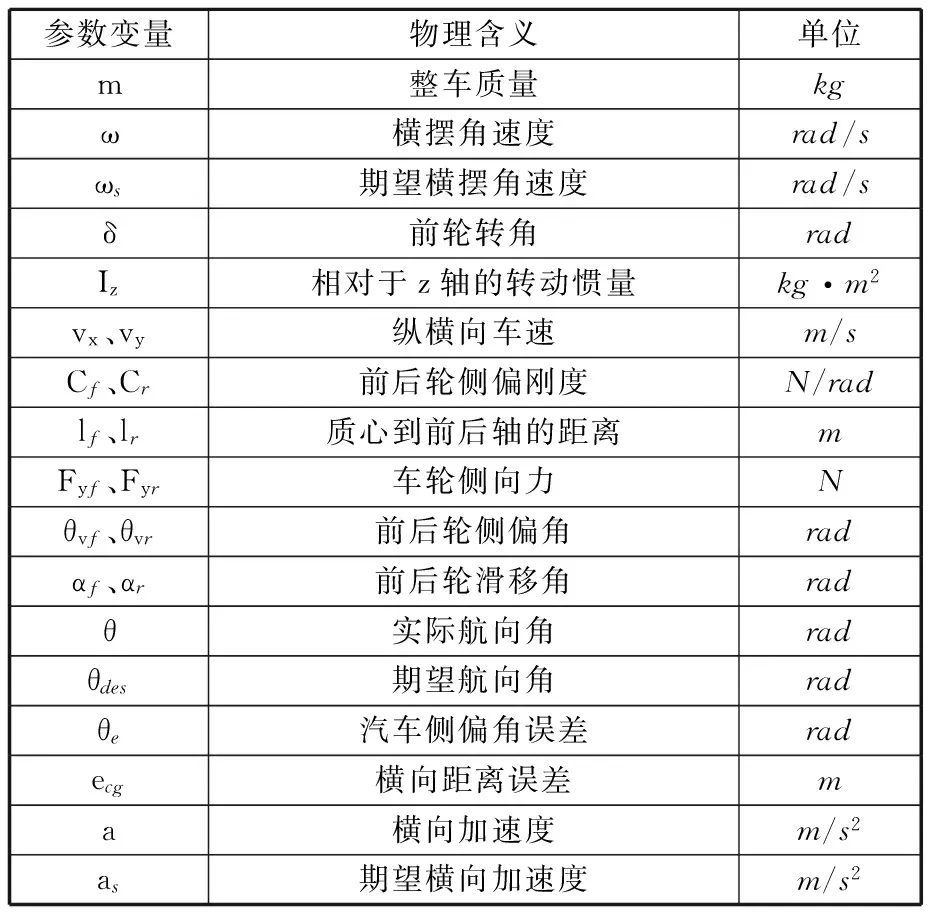
表1 整车模型参数及含义

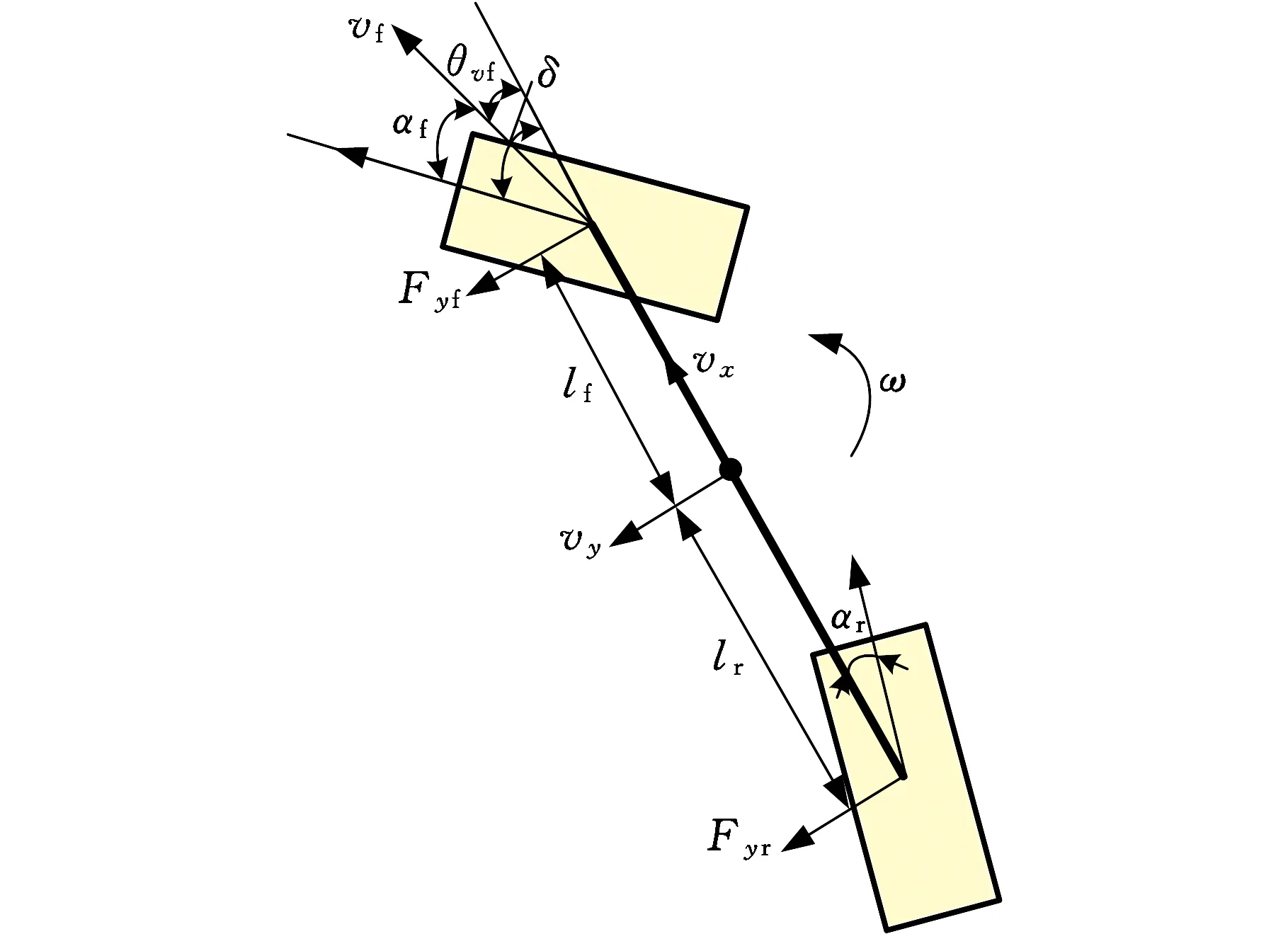
图1 二自由度汽车动力学模型

为减小模型的计算量，作如下假设：①忽略车辆悬架对控制系统的影响；②车辆行驶道路平坦，路况良好；③轮胎符合线性模型，忽略轮胎力的纵横向耦合关系；④忽略横纵向空气动力学[16]。

根据上述条件，沿着y轴和绕z轴的动力学方程为

(1)

根据小角度假设定理，可得到汽车前后轮侧偏角θvf、θvr:

(2)

汽车前后轮滑移角αf、αr为

(3)

则汽车前后轮受到的侧向力Fyf、Fyr为

(4)

将式(2)～式(4)代入式(1)中，可得到状态方程：

(5)

由车辆动力学模型分析可知，汽车横向控制问题主要是通过控制轮胎前轮转角来实现的。如图2所示，建立汽车质心处横向误差与期望轨迹模型，清晰描述车辆与车道线之间的动态关系。

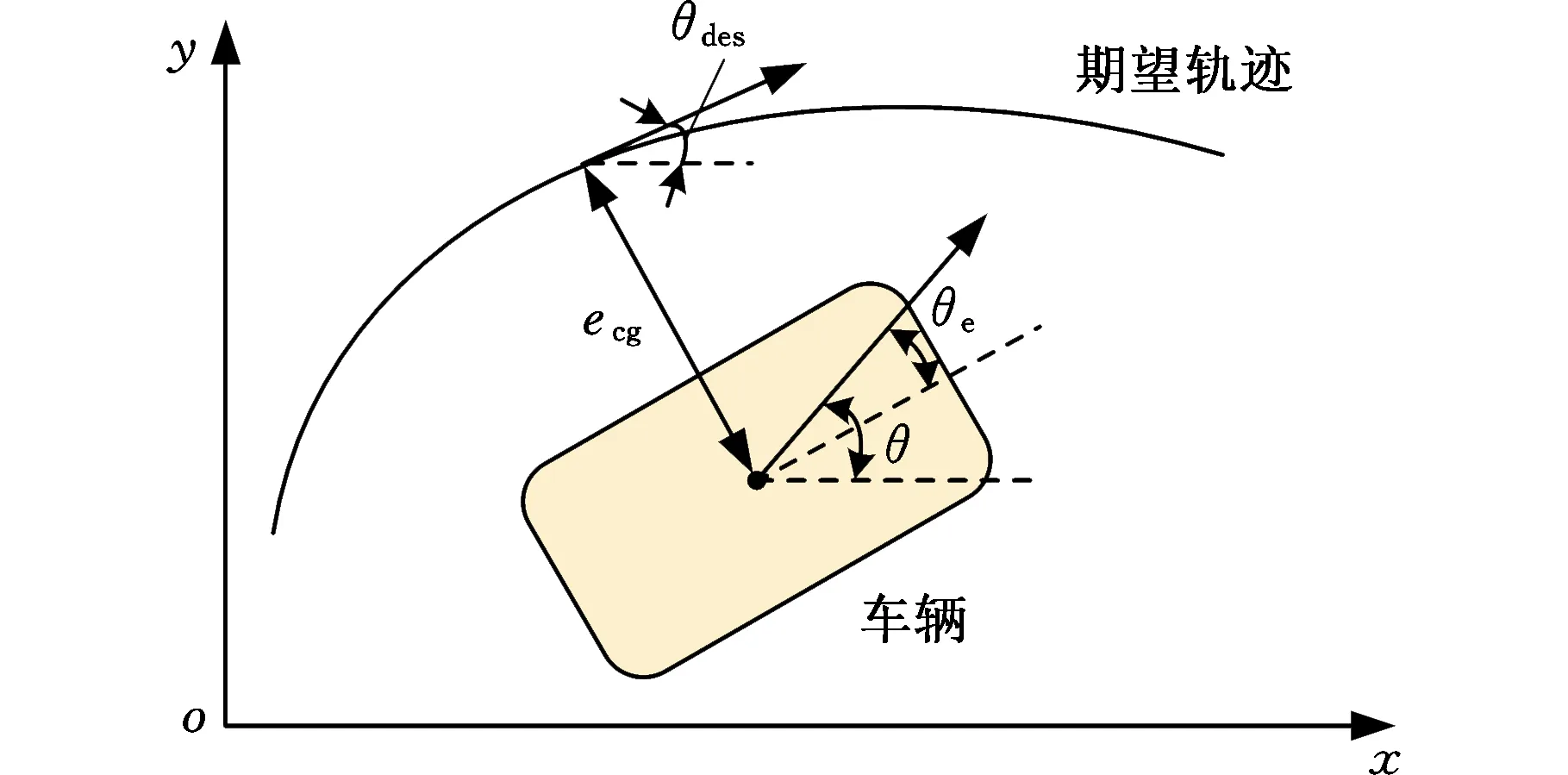
图2 汽车质心处横向误差与期望轨迹的关系

(6)

(7)

(8)

将式(6)～式(8)代入式(5)中，可得关于横向速度误差、横向加速度误差、侧偏角速度误差和侧偏角加速度误差的状态方程：

(9)

2 车辆横向控制策略

2.1 最优LQR横向控制算法

LQR是现代控制理论中最常用、最成熟的一种控制算法，在智能车辆无人驾驶的轨迹跟踪中应用较多。一般是利用期望轨迹及其曲率得到前馈控制量，然后计算车辆当前状态与期望轨迹之间的状态误差，采用LQR前馈控制和反馈控制相结合的方法，实现无人驾驶车辆轨迹跟踪[17]。本文将LQR横向控制算法的轨迹跟踪思想引入车道保持控制，以质心横向距离误差和侧偏角误差为输入变量，通过使性能指标函数取得最小值，最终求得最优期望前轮转角。采用LQR最优横向控制算法，可以满足系统快速性和实时性要求，使系统达到较好的性能，并且该算法简单，容易实现，在工程应用中具有重要意义。

(10)

根据实验车的相关参数，计算得到矩阵A两个特征根为0，说明状态方程不稳定，必须引入反馈控制。

可以求出秩R[B1AB1A2B1A3B1]=4，说明该系统可控，设计系统控制律为

(11)

式中，k1～k4为反馈矩阵K的4个元素。

采用线性二次型调节器计算矩阵K的4个元素。设Ad和Bd为矩阵A和B1的离散形式，则系统的输出可表示为

δ(k)=-Kx(k)

(12)

其中，R为加权系数，矩阵P满足黎卡提代数方程：

(13)

性能指标函数为

(14)

假定Q=diag(q11，q22，q33，q44)，为了简化计算，令q22=q33=q44=0。利用MATLAB可以求得矩阵K的4个元素，代入式(11)可以求出汽车最优期望前轮转角。

2.2 人机协同控制策略

李进等[18]提出了车道保持偏差的概念，即车道保持偏差与横向偏差和航向偏差有关，但在实际应用中，还需考虑车速条件。本文引入车辆偏离安全程度D，基于车辆横向距离误差ecg、车辆侧偏角误差θe和纵向车速vx共同确定D值大小，评估车辆偏离安全状态。所设计的模糊规则依据如下：当车辆发生偏离时，ecg、θe和vx值越大，车辆偏离车道中心线的趋势越快，则危险程度越高；反之则越低。模糊控制器的输入为横向距离误差、侧偏角误差和车速三个变量，输出为车辆偏离安全程度D。根据实车试验经验值，综合考虑了测试系统安全性和可靠性，设论域Uecg=[-0.3 m,0.3 m]；论域Uθe=[-0.01 rad,0.01 rad]；论域Uvx=[25 km/h,90 km/h]，其模糊子集均为{S,M,L}。输出量论域UD={0,1,2}，模糊子集为{Z,PM,PL}，分别表示安全状态、过渡状态和危险状态。输入、输出均采用三角形隶属度函数，具体模糊规则见表2。

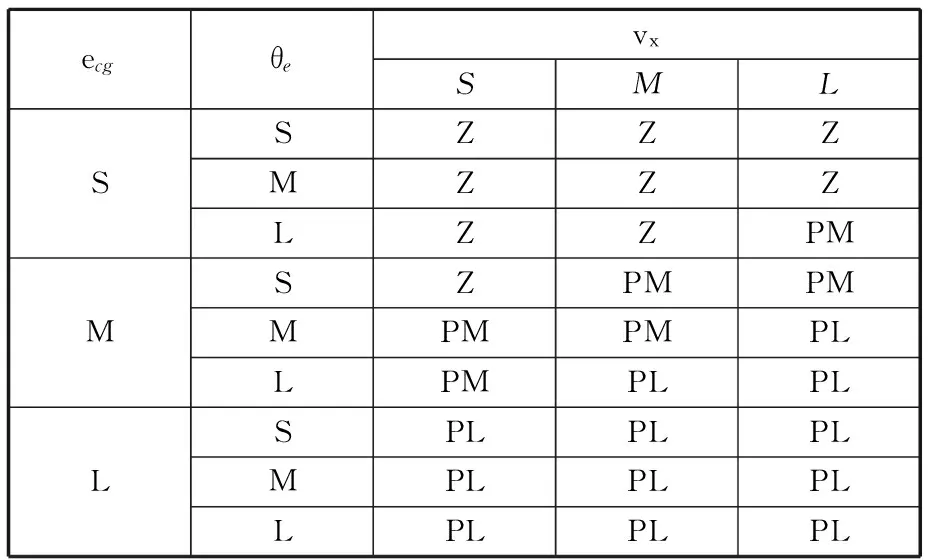
表2 模糊控制规则表

根据模糊规则控制表，进行车道保持系统模式判断。当车辆处于安全状态时，系统处于驾驶员模式，不干预车辆正常行驶；当车辆处于过渡状态和危险状态时，车道保持系统切换为助力纠偏模式，报警提示驾驶员车辆发生偏离并执行纠偏命令，将车辆纠回车道线内正常行驶。

欧盟新车安全评鉴协会和国际自动机工程师学会报告指出[19]，车道保持辅助系统应充分考虑控制系统安全性，避免人机冲突。为了更好地实现人机交互，本文根据车辆的偏离状态和车速信号对车辆进行安全评估，并采用扭矩控制策略，实现人机协同控制。人机协同控制结构如图3所示。

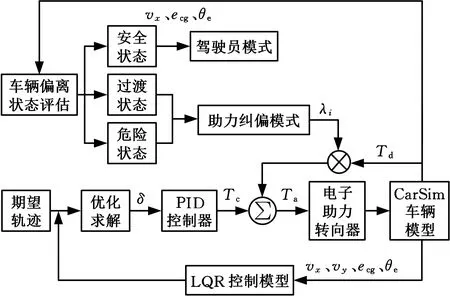
图3 人机协同控制结构图

车辆和道路传感器输出车路状态信息到LQR控制模型中，与车辆中心线位置进行比较后，通过最优求解器计算出最优期望前轮转角，经过PID控制算法输出助力扭矩Tc：

(15)

式中，KP、KI、KD别分为控制器的比例、微分、积分项系数；Δδ(t)为期望转角与实际输出转角的偏差值。

在助力纠偏模式下对驾驶员实际扭矩Td进行加权处理，最终输出的辅助扭矩Ta为

Ta=Tc+λiTdi=1,2

(16)

其中，λ1、λ2分别为过渡状态和危险状态的驾驶员实际扭矩加权系数。根据文献[20]前馈补偿模糊控制器设计思路，在实车测试试验中本文λ1、λ2取值分别为0.55和0.8，可以保证车道保持系统响较快，同时控制效果较好。

2.3 安全退出策略

在LKA系统工作时，还要考虑到驾驶员行为状态和外界环境的干扰。例如：驾驶员打开转向灯，意味着驾驶员有变道意图；驾驶员实际扭矩较大则为驾驶员欲强行介入驾驶操作，控制驾驶主动权；车轮越出车道边线距离较大，表示车辆已经偏离出本车道；车道线置信度较低说明道路环境较差。若在上述任何一种情况下执行LKA纠偏，易造成系统过分干预驾驶员操作，带来不适性和危险性，因此，本文针对此问题，提出一种安全退出策略，在不满足条件情况下LKA系统退出纠偏，切换到驾驶员控制模式，这样可保证驾驶员拥有最高驾驶权，实现驾驶相对安全性。安全退出策略框图见图4。图中，Td为驾驶员实际扭矩；L为车轮越出车道边线距离；C为车道线置信度；Tth、Lth、Cth分别为对应阈值。参考GB/T39323—2020《乘用车车道保持辅助系统(LKA)性能要求及试验方法》和实车测试试验，取Tth=1.5 N·m、Lth=0.4 m、Cth=2。

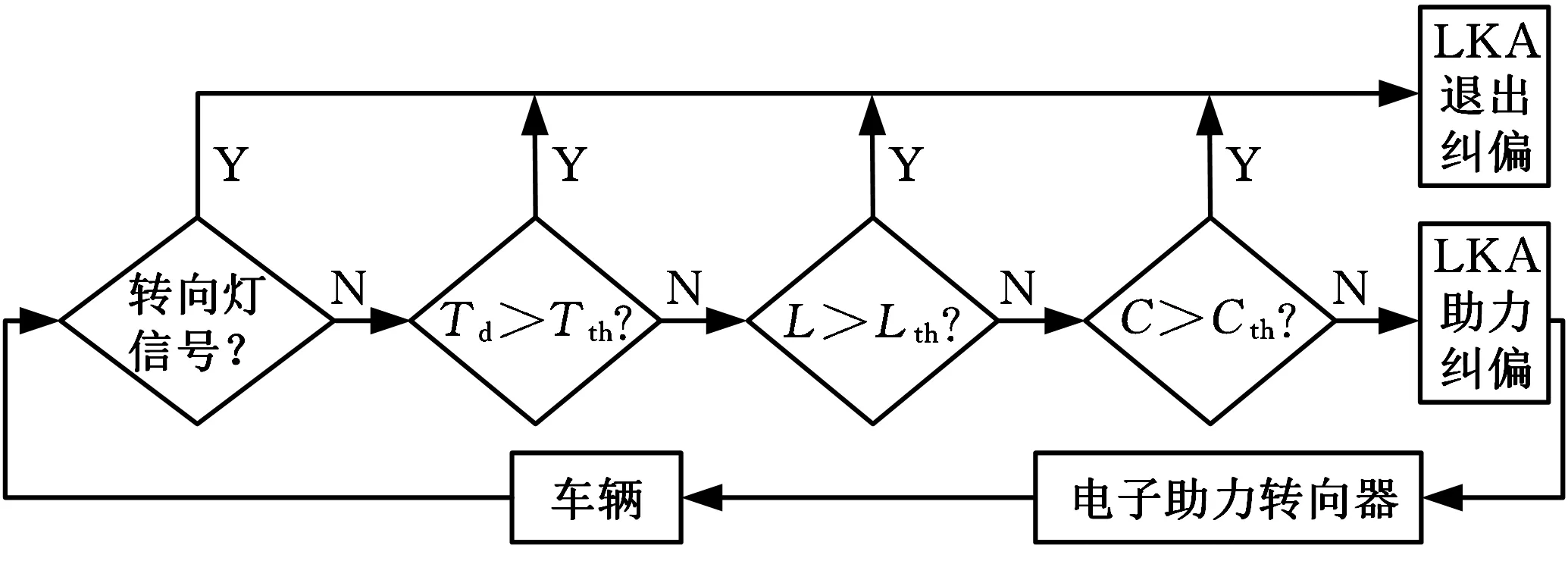
图4 安全退出策略框图

3 仿真与实车测试

3.1 仿真参数设置

为了验证本文所提横向控制算法的控制效果，基于CarSim/Simulink仿真软件平台，以车辆动力学模型为控制对象搭建闭环仿真模型。在CarSim中设置仿真模型的输入信号为驾驶员扭矩(IMP_STEER_T_IN)，输出信号为横纵向车速(Vx)、车辆航向角(Yaw)、质心纵坐标(Y0)、转向盘转角(Steer_SW)。仿真环境如图5所示。

图5 仿真环境

整车模型以CarSim中的Utility Truck为基础，修改其中部分车型参数值。车辆距离车道边线的初始距离值为0.3 m，车辆侧偏角初始角度为0.01 rad，仿真车速恒定为60 km/h，路面附着系数设置为0.85。假设初始条件设置均达到车道保持系统的激活条件，整车参数如表3所示。

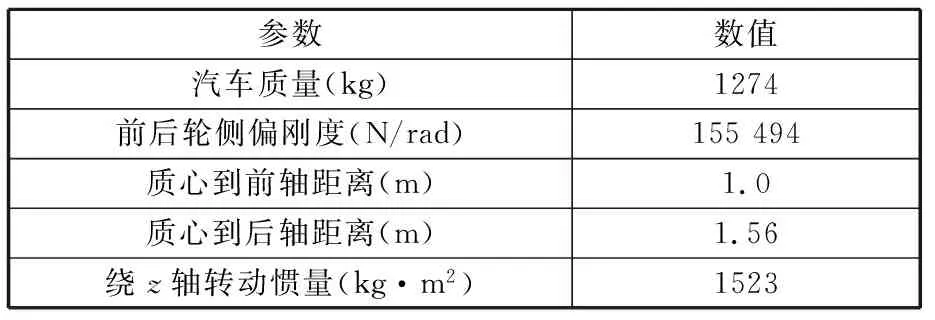
表3 仿真实验整车参数

3.2 横向控制算法仿真

仿真实验分为两部分：一是探究基于LQR-PID控制算法中不同Q、R参数对系统的影响，目的是验证控制算法的可行性，获得最优参数值；二是对比PID算法、预瞄-跟随算法和LQR算法，分析采用不同算法之间控制效果差异。

根据2.1节推导的系统状态方程，分析在前轮转角控制输入作用下，车辆横向距离误差和侧偏角误差的响应特性，结果如图6、图7所示。本文期望的响应特性是误差能够快速、稳定地趋近于零，并保持平衡。从仿真结果可以看出，不同的参数取值对车辆横向距离误差和质心侧偏角度误差影响较大。加权系数R增大表示控制输入尽可能小，当R=0.001时，横向距离误差和质心侧偏角误差较小，并最终能够趋近于0；矩阵Q中的元素增大表示偏差能够快速趋近于0，q11取值越大，系统收敛速度越快，但是质心侧偏角误差会相应增大。综合理论分析及多组实验数据，得出实车试验条件下一组优化参数R=0.001、q11=5。

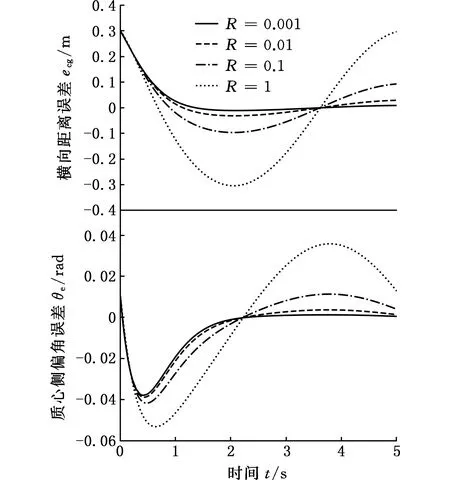
图6 加权系数R取不同值的仿真结果

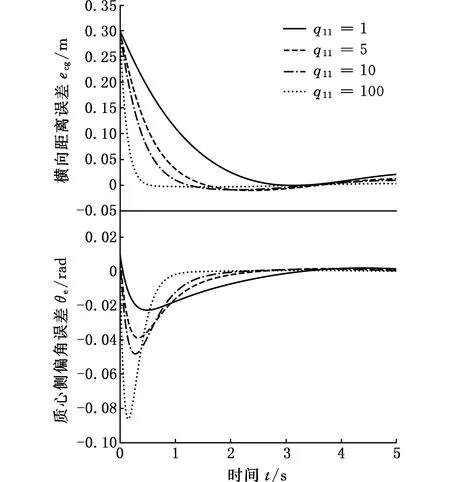
图7 矩阵Q取不同值的仿真结果

将本文所提出的LQR-PID算法与PID算法和预瞄-跟随算法相比较，结果如图8所示。图8a表明，三种控制算法均能实现车道保持功能。但本文算法系统响应速度更快，在2.0 s左右车辆便能够趋于车道中心线，且横向距离误差较小，可以使车辆保持在车道内，满足车道保持控制系统的要求。由图8b可以看出，质心侧偏角误差在-0.038～0.01 rad之间，但是能很快消除误差，表明车辆在纠偏过程中较平稳。

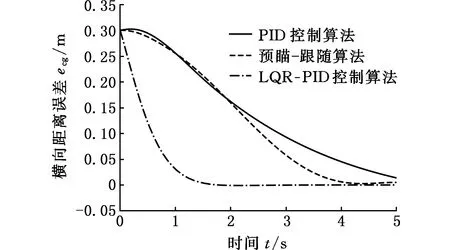
(a)横向距离误差

仿真实验验证了LQR-PID控制算法的有效性，系统快速响应更便于及时将偏离车辆纠回车道线内行驶，提高系统安全性，达到了设计目标。

3.3 实车试验

仿真实验结果表明，本文提出的LQR-PID控制算法能够实现车道保持控制功能，并且与PID控制和预瞄-跟随控制算法比较，LQR-PID算法具有更好的控制效果。在CarSim/Simulink仿真实验基础上，针对人机协同控制和安全退出策略进行实车测试试验，验证系统安全性。

Mobileye 630传感器是一款基于视觉系统分析和数据处理的辅助驾驶产品，其主机安装在车内前挡风玻璃中间位置，利用车辆、车道线、交通标志及行人检测技术，来测量车到左右车道线距离、车道线置信度和道路曲率等信息。此外，也能从车辆CAN总线获取车速和左右转向灯信号等信息。Mobileye 630主要性能参数见表4。

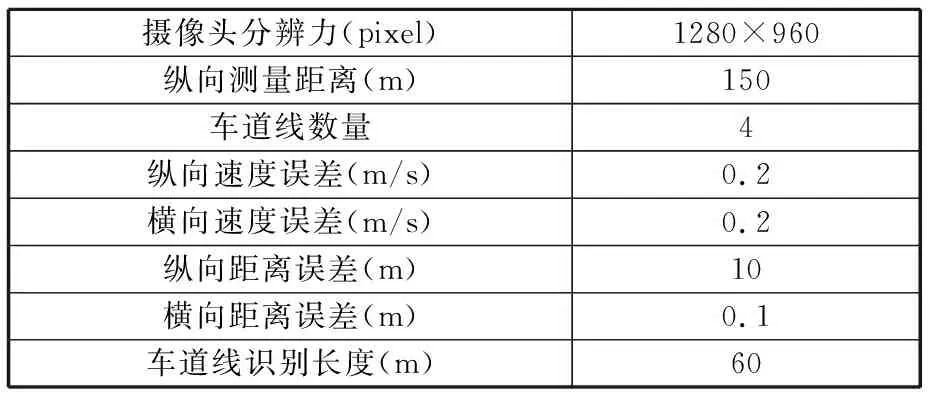
表4 Mobileye 630主要性能参数

本文采用Mobileye 630传感器感知周围环境，主要获取车道线距离、车道线置信度和计算出车轮到车道边线距离等。选用江淮轻卡试验车，设计基于STM32的车道保持控制器；采用电子助力转向器(electric power steering，EPS)作为车道保持系统的执行机构，并且EPS安装扭矩和转角传感器，可以检测驾驶员实际扭矩和转向盘转角值。各硬件系统间采用CAN总线连接。实车试验平台如图9所示。

图9 实车试验平台

3.3.1车道保持人机协同控制试验

如图10所示，在1.8 s内车辆发生偏离但处于安全状态，系统未输出辅助扭矩。1.8 s后，横向距离误差大于设定阈值，启动辅助模式，辅助扭矩增加，LKA系统执行纠偏动作。整个纠偏过程由驾驶员模拟分心状态，采用分辨力为0.2 N·m的扭矩传感器检测驾驶员实际扭矩值，由图10a看出，扭矩范围为±0.6 N·m。试验结果表明，该人机协同控制的车道保持辅助系统实现了纠偏功能，使车辆纠回车道中心线附近稳定行驶。

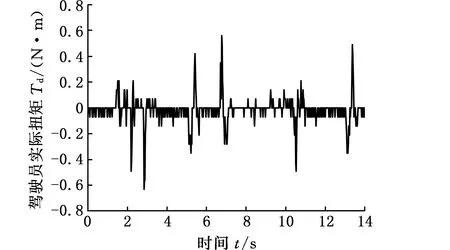
(a)驾驶员实际扭矩

3.3.2安全退出策略试验

安全退出策略试验结果如图11所示，图11a为驾驶员开启转向灯试验，在6.1 s(即A点)时转向灯标志位置1，表明驾驶员参与操控车辆，此时辅助扭矩缓慢降为0，辅助系统退出纠偏，将驾驶权完全移交给驾驶员。图11b为驾驶员实际扭矩试验，在4.0 s(即B点)之前，驾驶员实际扭矩较小，当车辆发生偏离时，系统认为驾驶员没有参与，输出辅助扭矩，执行纠偏功能；当驾驶员实际扭矩超过1.5 N·m的阈值时，系统认为驾驶员参与转向盘控制，则辅助扭矩降为0，系统退出纠偏。对于图11c、图11d，则分别是车轮越线过多和车道线置信度较低，在C点和D点处不能满足车道保持的激活条件，均退出纠偏。试验结果表明，当人-车-路状态条件不满足车道保持辅助系统的激活条件时，系统能够及时退出纠偏，防止系统过多干预驾驶员，提高了系统安全性。

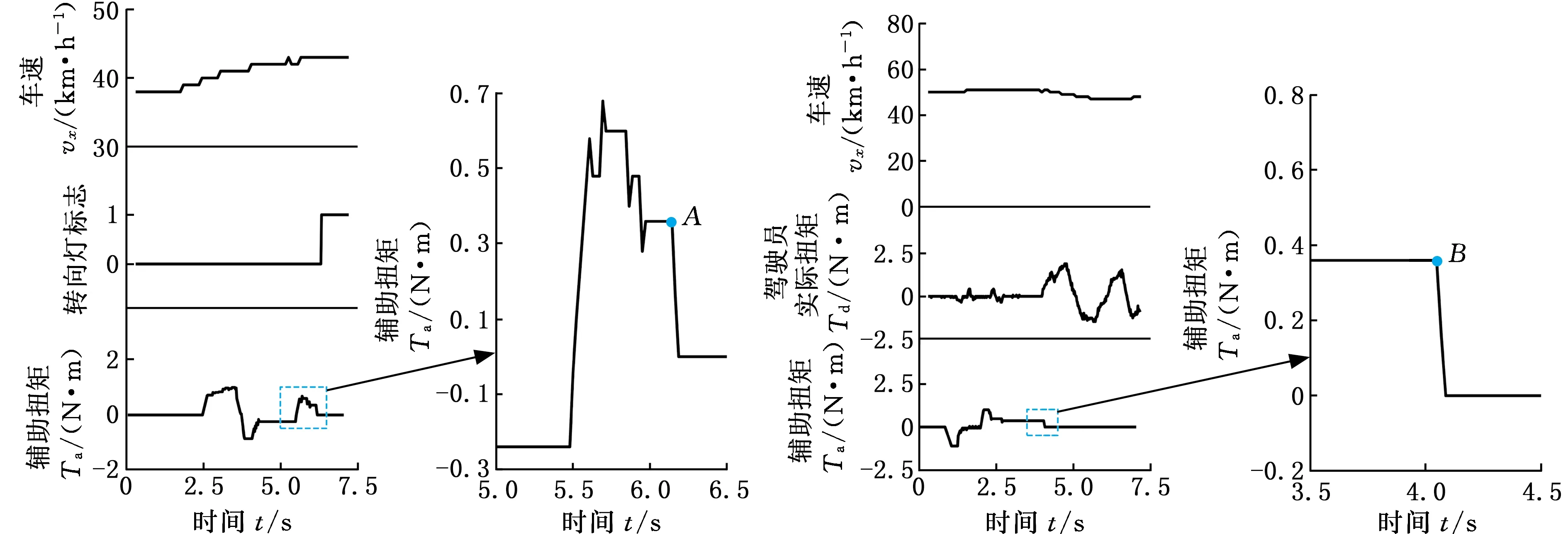
(a)驾驶员开启转向灯试验 (b)驾驶员实际扭矩试验

4 结论

(1)本文基于车辆动力学模型，提出一种LQR-PID横向控制方法，通过CarSim/Simulink软件平台进行联合仿真，验证了LQR-PID算法不仅可以保证车辆稳定地在车道中心线附近安全行驶，且响应速度更快。

(2)本文在仿真实验的基础上，基于横向距离误差、侧偏角误差和车速，对车辆偏离状态进行安全评估并设计了辅助系统安全退出策略，实车试验结果表明，该系统在不满足条件时能够及时退出纠偏，避免人机冲突，保证驾驶员的绝对驾驶权，实现车道保持功能和系统安全性能。