风洞上攻角机器人轨迹规划算法研究与实现

孙晓军 宋代平 林敬周 韩伟航

1.重庆大学机械传动国家重点实验室,重庆,4000442.中国空气动力学研究与发展中心超高速空气动力研究所,绵阳，621000 3.辽宁石油化工大学信息与控制工程学院, 抚顺，113001

0 引言

机械臂的目标轨迹往往先通过试教法确定，再通过轨迹规划算法确定各个关节的速度曲线。传统的轨迹规划算法仅考虑了机械臂运动学模型的非线性及关节电机速度的限制，这使得规划的轨迹不能充分发挥机械臂的工作效率。对目标轨迹进行二次规划可提高机械臂的运动速度，缩短运动时间。与传统的轨迹规划算法相比，基于动力学模型的轨迹规划算法能够充分考虑机械臂运动学模型、动力学模型的非线性，以及关节速度、力/力矩的限制，规划轨迹能够充分发挥机械臂驱动能力，但该算法存在计算量大、计算效率低的问题[1]。

目前考虑机械臂动力学模型的轨迹规划算法有3类。一是相平面法，通过引入路径参数，对机械臂的运动学模型、动力学模型进行参数化变换，得到以路径参数二阶微分方程表示的路径参数化动力学模型，再通过路径参数化模型将关节速度、力/力矩等约束转化为关于路径参数的约束，最终将轨迹规划问题转化为关于路径参数的二维优化问题[2-4]。相平面法计算效率高，但通用性较差，约束增加困难，如考虑加加速度约束，相平面法解算将变得复杂[5]。二是直接优化方法，通常将目标轨迹划分为n段，将规划问题转化为具有n个不等式约束(动力学约束、运动学约束、关节力矩约束等)的优化问题，然后采用如凸优化法[6-10]等相对高效的优化算法进行优化处理。凸优化法具有较高的通用性，约束添加简单，但依赖于高效的优化算法包，计算效率低于相平面法。三是采用最优控制理论的时间最优控制方法，通过求解最优性必要条件的两点边值问题获得最优解[11]，该方法在理论上比前两种算法速度快，但规划的轨迹易引起运动学奇异的问题[5]。

由于相平面法具有较高的计算效率，因此本文采用相平面法进行速度曲线规划，并对相平面法进行优化改进以进一步提高算法的计算效率，对规划的轨迹进行平滑处理以保证机械臂运动平稳。相平面法优化方法体现在以下三点：①通过模糊推理计算路径点数目，减小计算规模，采用0值加速度曲线乘以比例系数替代关节力/力矩约束最大速度曲线，提高算法的计算效率；②通过速度特征点法提取多重约束最大速度曲线的速度特征点，再通过B样条插值法对速度特征点插值，保证速度曲线连续光滑；③采用修型-射靶算法对速度曲线进行修形，得到满足多重约束的最大速度曲线。

1 动力学模型路径参数化

机械臂的动力学模型可以表示为

(1)

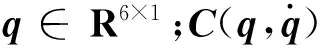
设机械臂在工作空间的目标轨迹为s(P)(∀s∈R+)，P∈Rn×6为目标轨迹的路径点向量。目标轨迹的时间参数化可表示为s(t):[0,T]→[ss,se]，T为机械臂跟踪目标轨迹的运动时间，s为一维路径参数，ss为起始路径参数值，se为末端路径参数值。

在关节空间，根据机械臂运动学模型可得机械臂末端的正运动学特征：

p=Z(q)

(2)

(3)

(4)

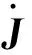
在参考坐标系，采用路径s表示机械臂末端的正运动学特征：

p=f(s)

(5)

(6)

(7)

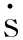
结合式(2)～式(4)可得关于路径参数s的运动学模型：

q=Z-1(f(s))

(8)

(9)

(10)

将式(8)～式(10)代入式(1)，可得关于路径参数s的动力学模型：

(11)

(12)

(13)

(14)

a4(s)=G(q(s))+JTτd(q(s))

(15)

2 多重约束下的最大速度曲线

2.1 目标轨迹路径特征点的提取

机械臂目标轨迹的路径点向量P(P=(P1,P2,…,PK))一般提前设定，通过运动学逆解求解其对应的关节向量q(q=(q1，q2，…，qK))。为了使机械臂平稳通过路径点，采用B样条等曲线对路径点向量P进行插值得到连续的目标轨迹。轨迹二次规划需要将目标轨迹进行离散化处理，进而将轨迹规划问题转化为稀疏离散化优化问题。若离散的位姿向量序列过大将导致优化规模过大，降低轨迹规划算法的效率；若位姿向量序列过小将丢失目标轨迹的特征，甚至失真。在此采用目标轨迹的路径复杂程度与动力学模型非线性程度作为提取目标轨迹路径特征点的依据，使用模糊推理算法计算路径特征点的间隔，等间距提取路径特征点。

(16)

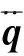
结合式(1)、式(8)、式(9)可得向心加速度/科氏加速度单位向量

(17)

结合式(1)、式(8)可得重力加速度单位向量

γg=a4=[JT]-1G(Z-1(f(s)))

(18)

路径特征点算法流程图见图1，算法步骤如下。

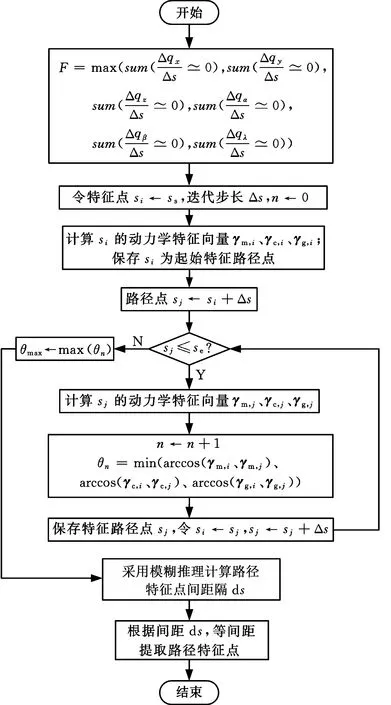
图1 路径特征点算法流程图

(1)根据下式计算路径复杂度：

(19)

式中，Δs为迭代步长；Δqx、Δqy、Δqz为机器人末端在参考坐标系下x、y、z方向的微分变化量；Δqα、Δqβ、Δqγ为机器人末端在参考坐标系下绕x、y、z轴旋转的角度微分变量；sum(·)为求和函数。

(2)计算动力学模型非线性程度。令迭代步长为Δs，计算路径点si=ss的动力学特征向量γm,i、γc,i、γg,i，再计算路径点sj=si+Δs的动力学特征向量γm,j、γc,j、γg，j，计算si与sj特征向量的夹角θn，刷新si=sj、sj=si+Δs，若sj=si+Δs>se，则θmax=max(θn)为动力学模型变化程度。

(3)采用模糊推理计算路径特征点间隔ds。利用路径点间隔ds等间距提取路径特征点序列，令得到的路径特征点向量P′=(P1，P2，…，PN),N≥K，对应的关节向量q′=(q1，q2，…，qN)。

2.2 关节速度约束下的最大速度曲线

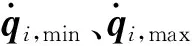
(20)

将式(9)代入式(20)可得关节i速度边界限制的最大速度：

(21)

通过式(21)依次求解机械臂各个自由度速度边界限制的最大速度曲线，然后通过下式求解所有关节速度边界限制得到的最大速度ζv：

(22)

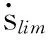
依次求解路径特征点的最大速度ζv，得到关节速度边界限制的最大速度曲线V1：

V1={ζv(s),s∈[0,1]}

(23)

2.3 关节加速度/力矩约束下的最大速度曲线

关节力矩约束表示为

Tmin≤τ(s)≤Tmax

(24)

其中，Tmin∈R6×1、Tmax∈R6×1，为机械臂关节力矩边界。将式(11)代入式(24)可得

(25)

为了表述方便，式(25)可表示为

(26)

分析式(26)有以下三种情况：

(1)a1,i(s)>0时，有

定义加速度的上边界β为

(2)a1,i(s)<0时，有

定义加速度的下边界α为

(3)a1,i(s)=0时为零惯性点，不予考虑。

依次求取各个关节力矩限制的加速度，可得路径加速度边界：

(27)

i=0,1,…，6

至此得关节力/力矩约束转化为对路径加速度的约束：

(28)

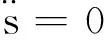
2.4 启动/停止最大速度曲线

机械臂在启动时希望机械臂以最大的加速度沿着目标路径轨迹运动，采用数值积分[12]方法求解启动速度，计算公式如下：

(29)

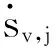
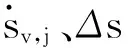
(30)

启动/停止最大速度曲线的获取步骤如下：

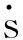
(2)类似地，在停止运动时以最小的加速度减速运动，采用逆向积分的方法求解停止最大速度曲线V5。

2.5 多重约束下最大速度曲线的生成

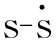
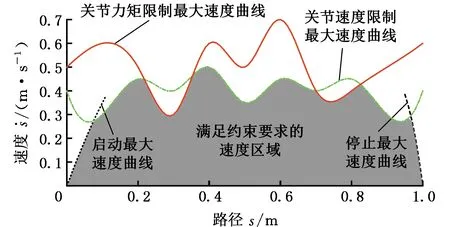
图2 多重约束最大速度曲线的生成

3 最大速度曲线的优化

由于2.5节求得的最大速度曲线Ve可能存在加速度不连续等问题，故需对Ve进行优化。最大速度曲线Ve的优化分为速度特征点的获取、速度特征点B样条插值[13](或其他平滑插值算法)和修型-打靶算法修正速度特征点幅值三步。

最大速度曲线Ve速度特征点的提取方法为：提取最大速度曲线Ve的首尾速度Ve,0、Ve,K；令i←3，若Ve,i-1≥Ve,i≤Ve,i+1，则Ve,i为特征速度点，否则令i←i+1，依此再进行判断，扫描所有最大速度曲线Ve离散点；若速度特征点数目小于4，对速度特征点数进行等间距插值。

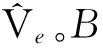
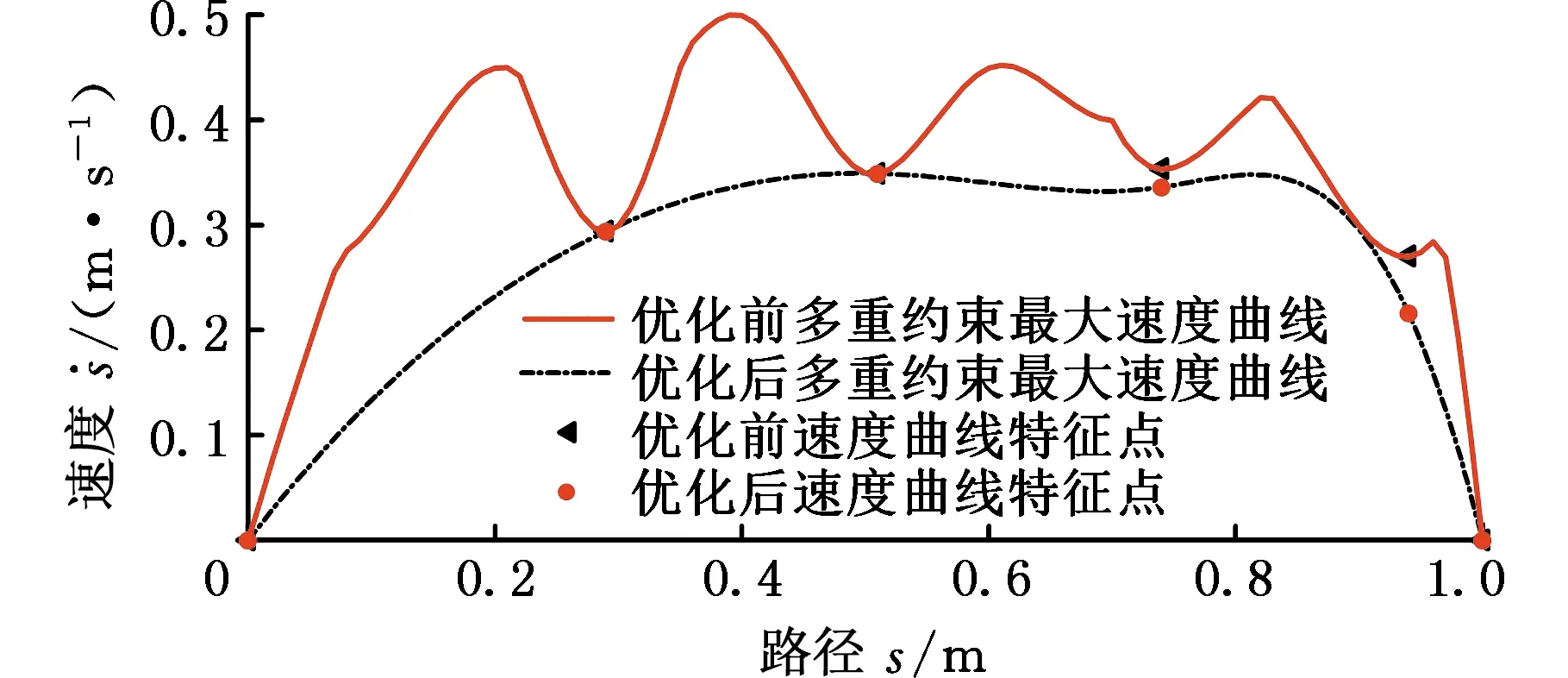
图3 B样条插值速度特征点

修型-打靶算法流程图见图4，算法的流程如下：

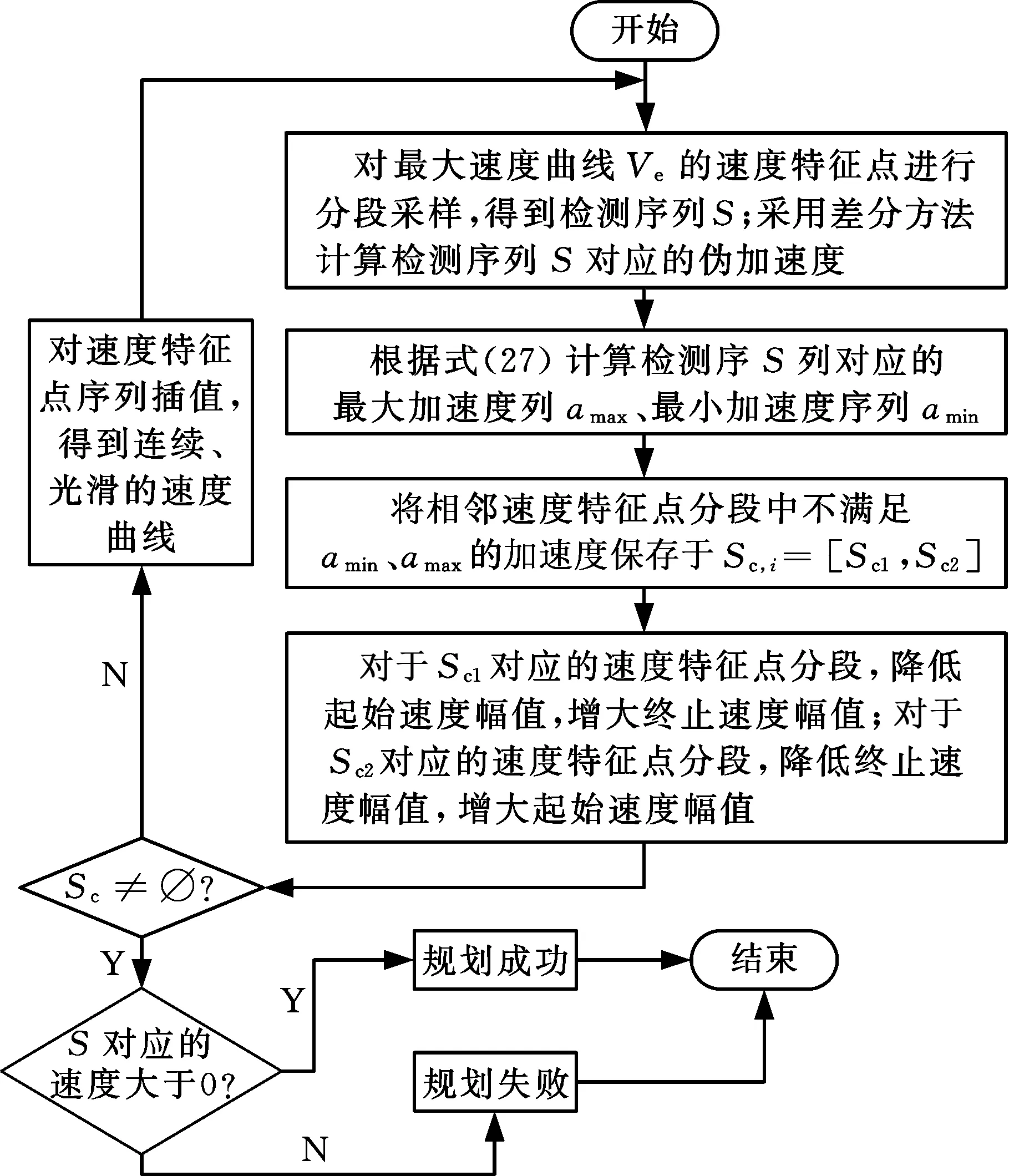
图4 修型-打靶算法流程图

(1)对最大速度曲线Ve进行分段采样得到检测序列S，采用差分方法计算检测序列S对应的加速度as。

(2)根据式(27)计算得到检测序列S对应的最大加速度序列amax、最小加速度序列amin。

(3)依次检查加速度as是否满足约束要求，将不满足amin、amax的加速度保存在Sc,i=[Sc1,Sc2]，其中Sc,i表示第i个相邻速度特征点分段，Sc1表示小于amin序列所对应的加速度，Sc2表示大于amax序列所对应的加速度。

(4)若Sc1非空，则降低Sc1序列所对应的速度特征点分段的起始速度幅值，增大终止速度幅值；若Sc2非空，则降低Sc2序列所对应的速度特征点分段终止速度幅值，增大起始速度幅值。

(5)若Sc非空，则重复步骤(2)～步骤(4)修正速度幅值，直到Sc为空，若检测序列S所对应的速度非负，则认为修形后的最大速度曲线满足关节速度、关节力矩/加速度要求，若检测序列S所对应的速度为负，则规划算法失效。

4 实验

为验证速度曲线规划算法的有效性，以六自由度上攻角机械臂为例验证轨迹规划算法的有效性及计算效率。上攻角机械臂的结构简图见图5，包括轴向X、法向Y、侧向Z、俯仰α、偏航β、滚转γ六个自由度，飞行器模型挂载在滚转机构末端，各个自由度的力矩/电流约束、速度约束如表1所示。

表1 关节力矩/电流约束、速度约束表

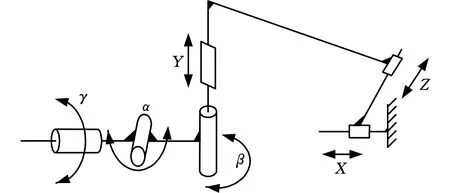
图5 上攻角机械臂结构简图

轨迹规划算法编写在监控PC(CPU 主频为2.3 GHz、内存为 7.9 GB)的MATLAB 2016软件上，监控PC上的人机交互界面软件通过MATLAB接口调用轨迹规划算法，并将规划结果通过ADS通信传输给工控机。工控机运行机械臂的运动控制软件，完成机械臂的运动控制及各个关节位置、速度、电流等数据的采集。

4.1 算法有效性实验

4.1.1简单轨迹规划实验

为了验证速度曲线规划算法的有效性，进行特定轨迹规划实验。定义简单目标轨迹的起始位姿(-500 mm,-100 mm,0,-8°,0°,0°)T与终点位姿(0,600 mm,0,0°,0°,0°)T，起始位姿与终点位姿采用B样条插值得到连续的轨迹。通过动力学特征向量法提取有限数目路径特征点，路径特征点在各个自由度的分布如图6所示。

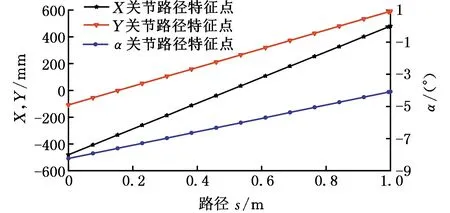
图6 X、Y、α轴的路径特征点的分布

比例系数Kv=1.2，通过MATLAB计算得到关节速度约束、关节力矩约束、启动/停止约束等约束的最大速度曲线，对上述约束曲线取向下交集可得到多重约束下的最大速度曲线MV1，如图7所示。不难看出最大速度曲线MV1存在突变，易引起上攻角机械臂振荡而影响系统精度，因此需要对最大速度曲线MV1进行平滑处理。

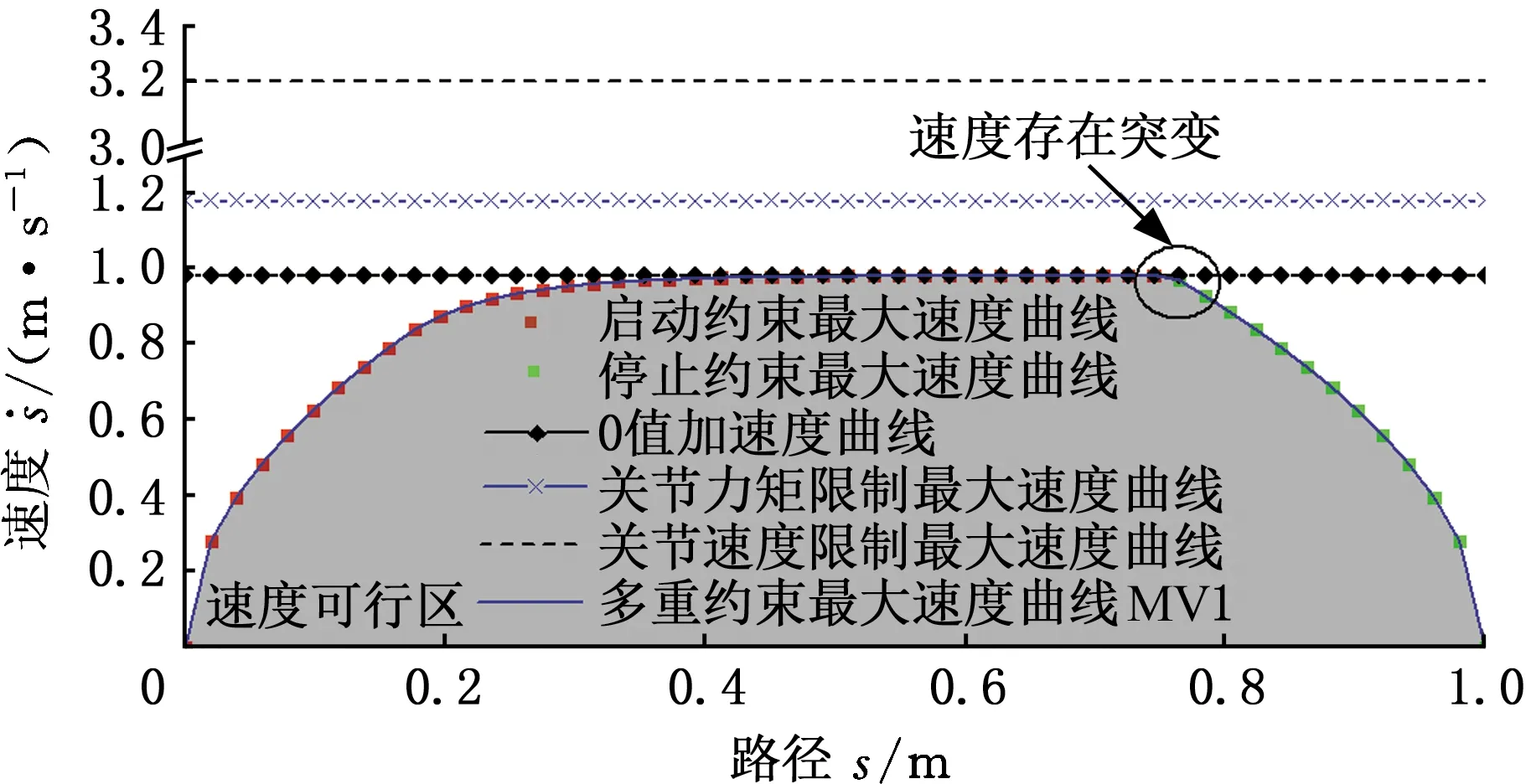
图7 简单目标轨迹相平面

提取最大速度曲线MV1的特征速度点，然后采用B样条插值[14]得到连续光滑的最大速度曲线MV2。B样条插值可能导致最大速度曲线MV2在P1、P2处超过最大速度曲线边界(图8)，超出最大速度曲线边界的速度段不满足关节速度或关节力矩/加速度的约束限制，为此采用修型-打靶算法矫正速度特征值，进而实现对最大速度曲线MV2的修形，使得最终的速度曲线满足关节速度、关节力矩/加速度等约束条件，如图8所示。

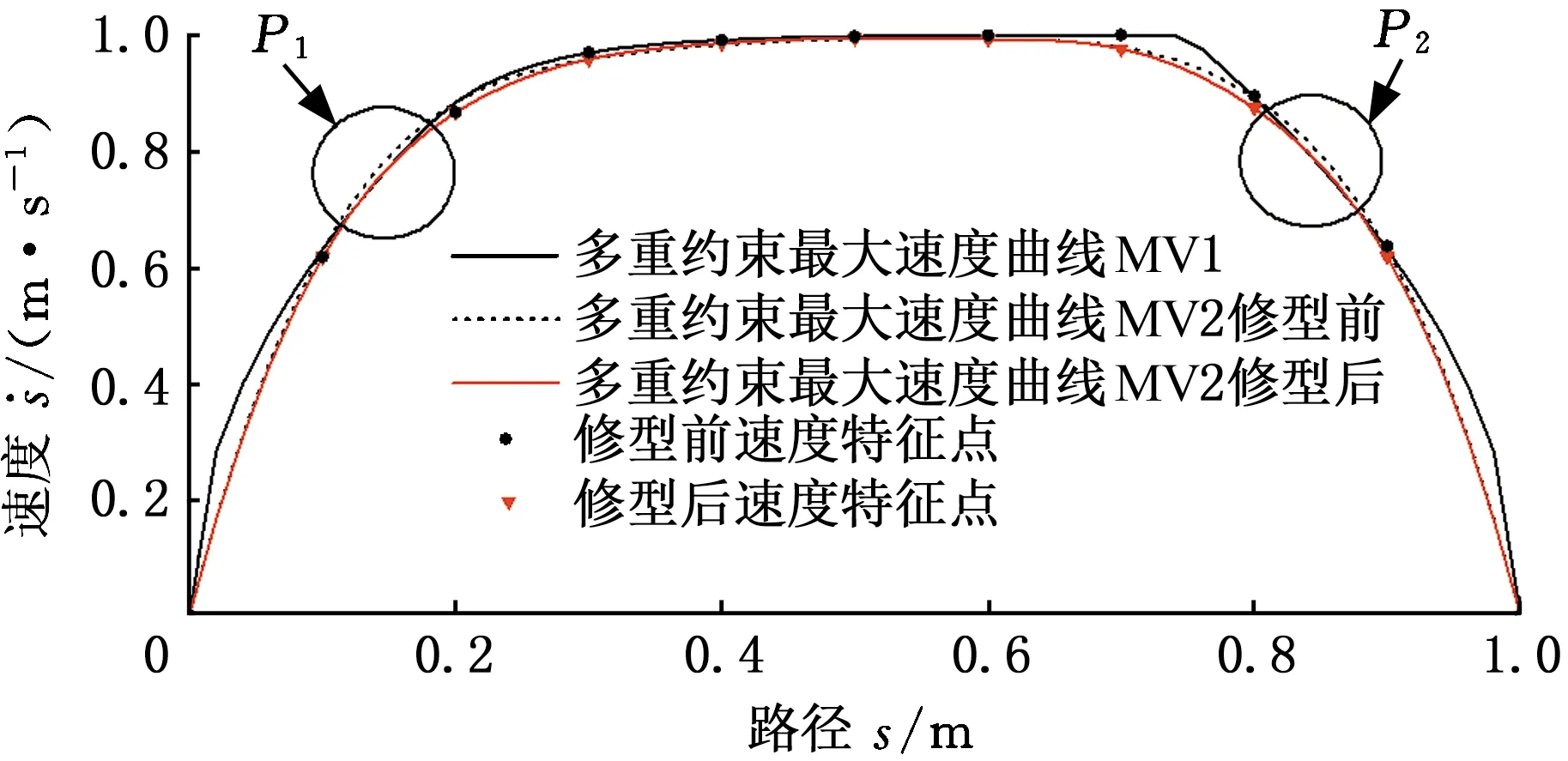
图8 修型-打靶算法修正速度特征点

通过数值计算可得到速度曲线MV2、加速度曲线MVA2在时间轴的表示，如图9、图10所示。不难看出，速度曲线变化连续平滑，不存在突变线性，加速度曲线除了在启动与停止时刻为满足加速、减速特性加速度不为零外，其他时刻都连续平滑。综上所述,规划得到的速度曲线满足对速度、加速度轨迹连续光滑的要求。

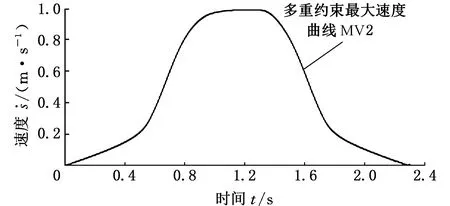
图9 简单轨迹相平面

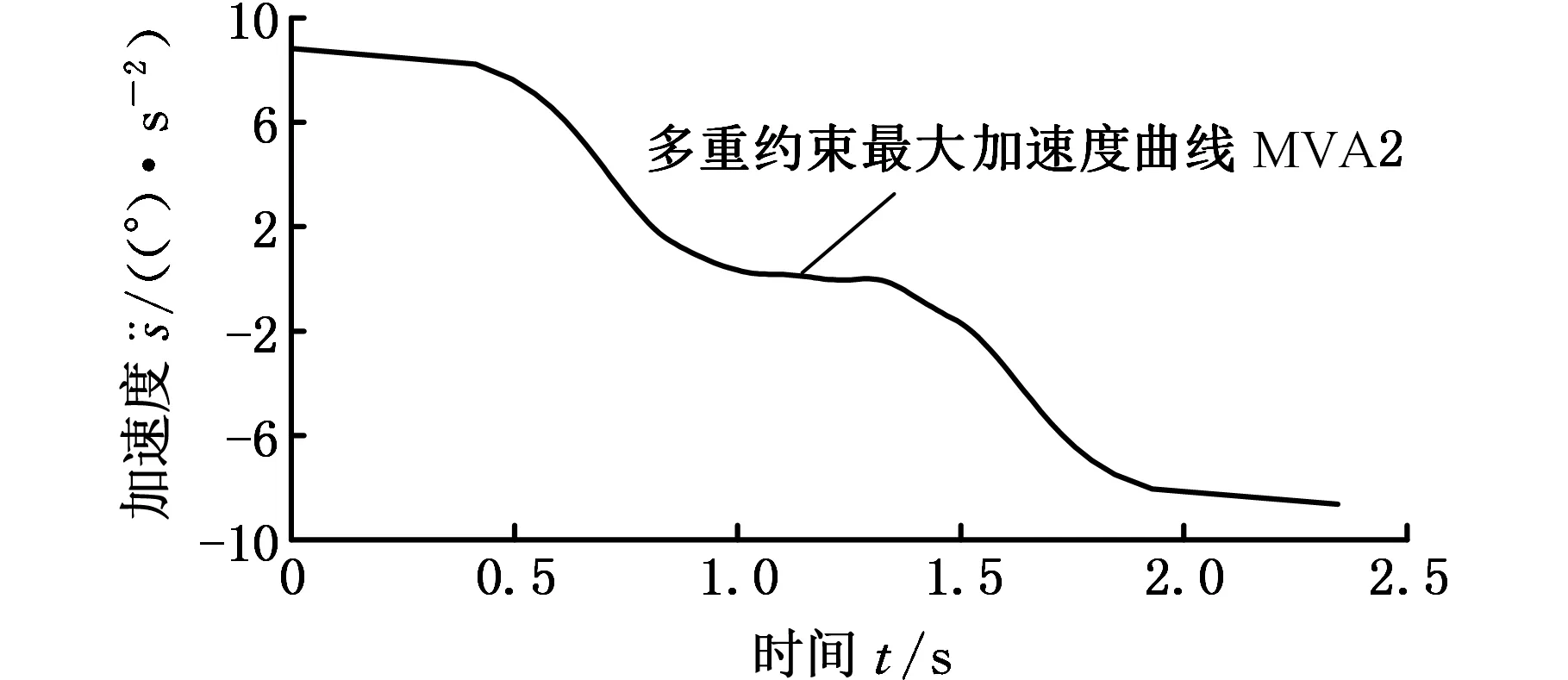
图10 简单轨迹相平面

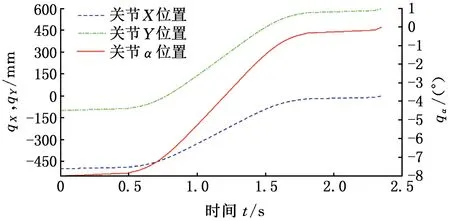
图11 关节位置曲线

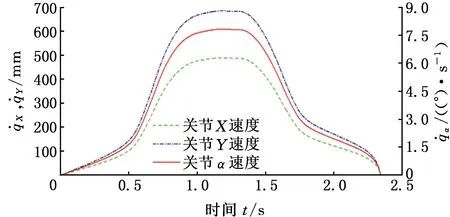
图12 关节速度曲线

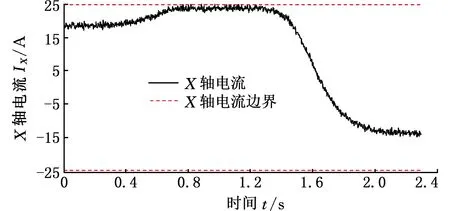
图13 X轴关节电流曲线

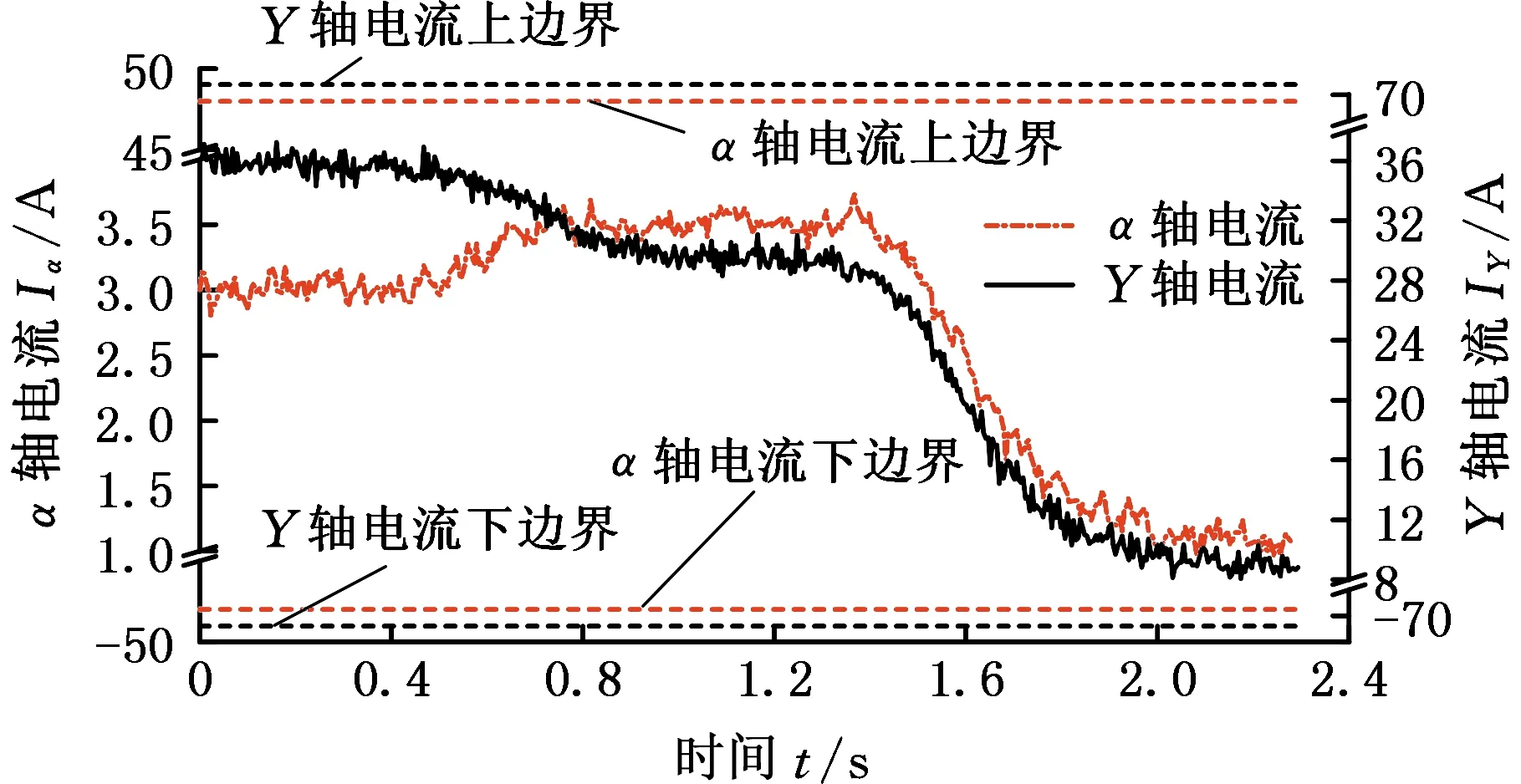
图14 Y、α轴关节电流曲线

4.1.2复杂轨迹规划实验

为了进一步验证速度曲线规划算法对复杂轨迹规划的有效性，图15、图16给出了复杂目标轨迹对应的上攻角机械臂关节曲线。

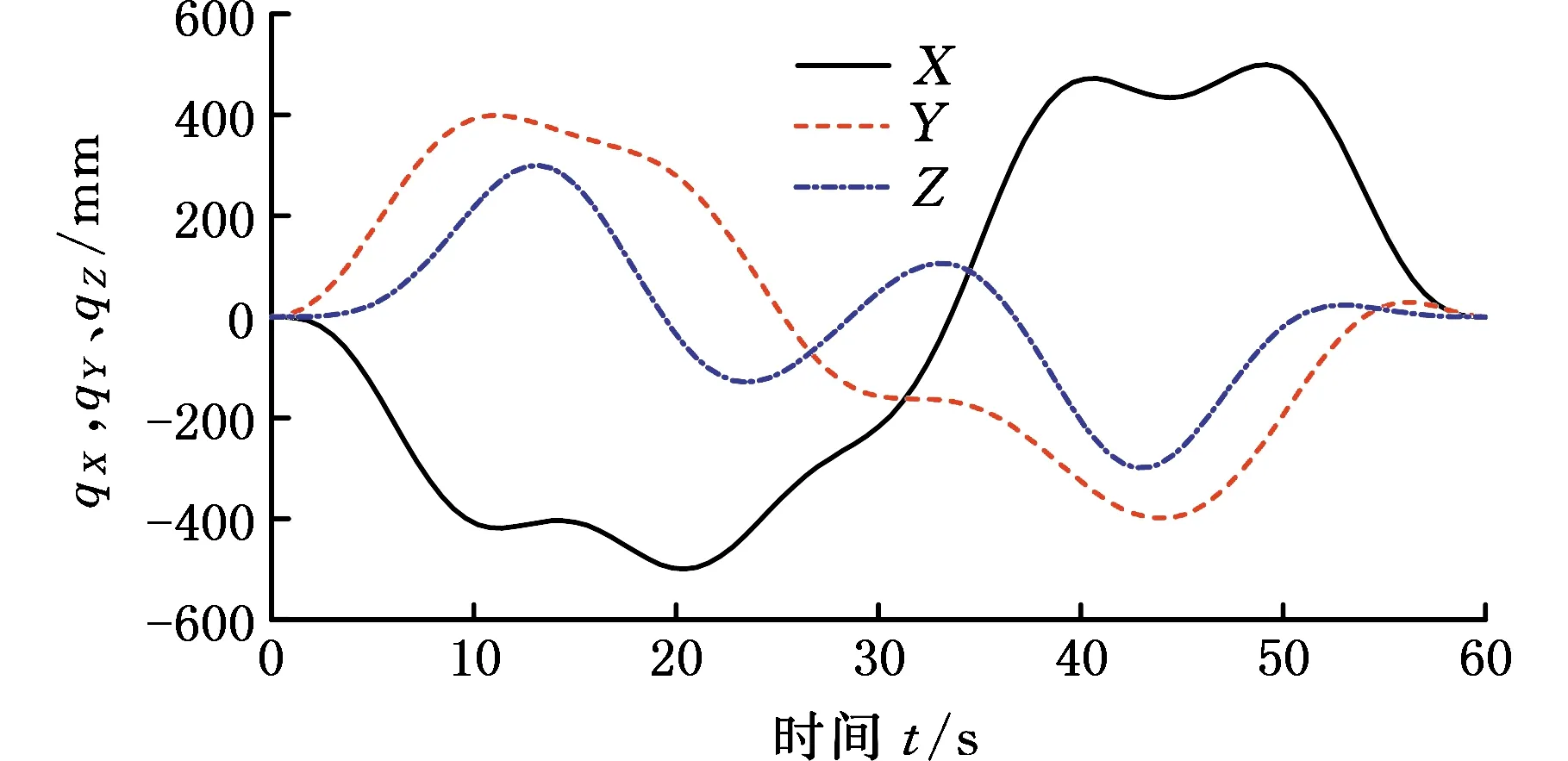
图15 X、Y、Z自由度激励轨迹曲线

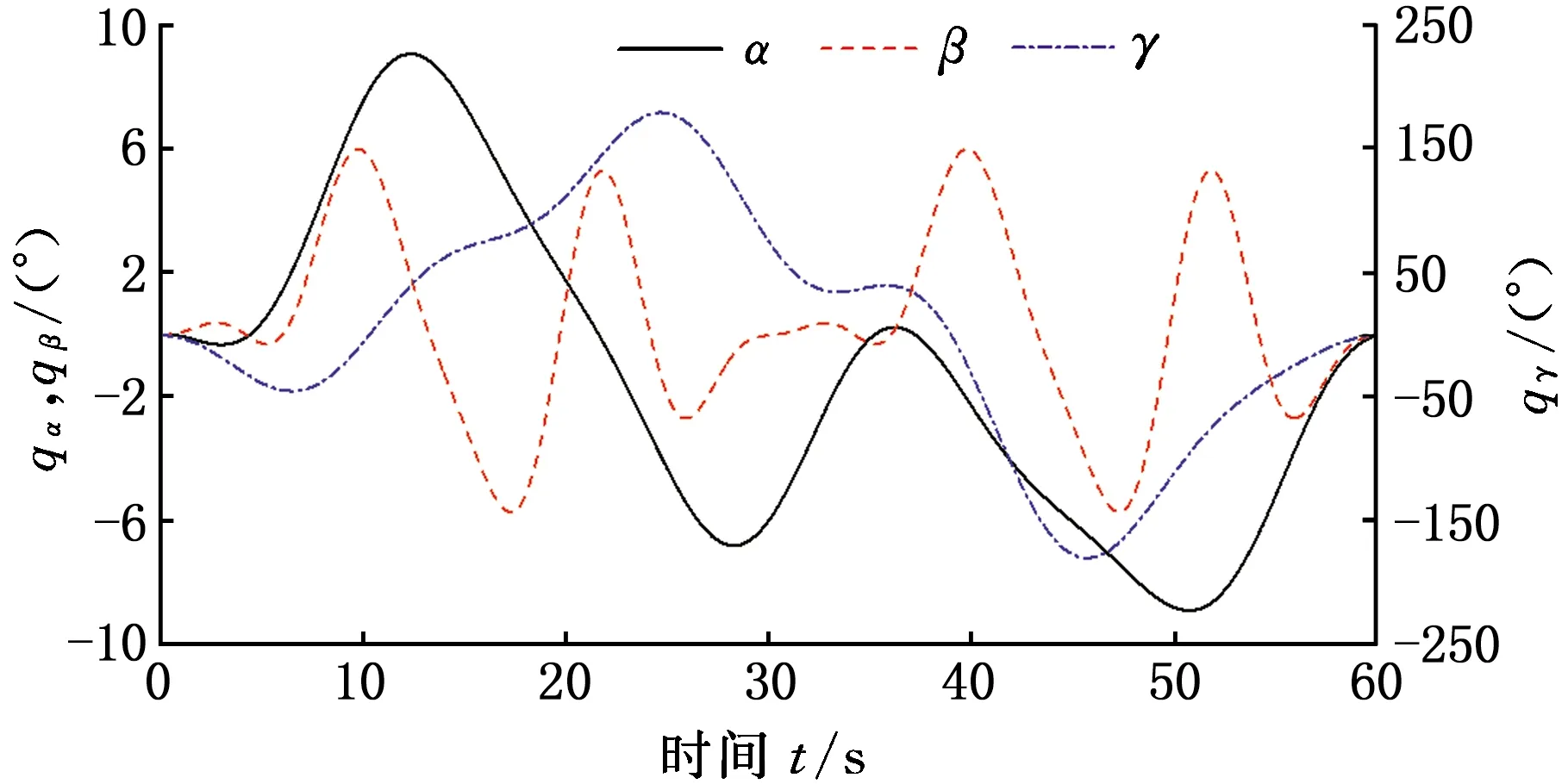
图16 α、β、γ自由度激励轨迹曲线

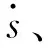
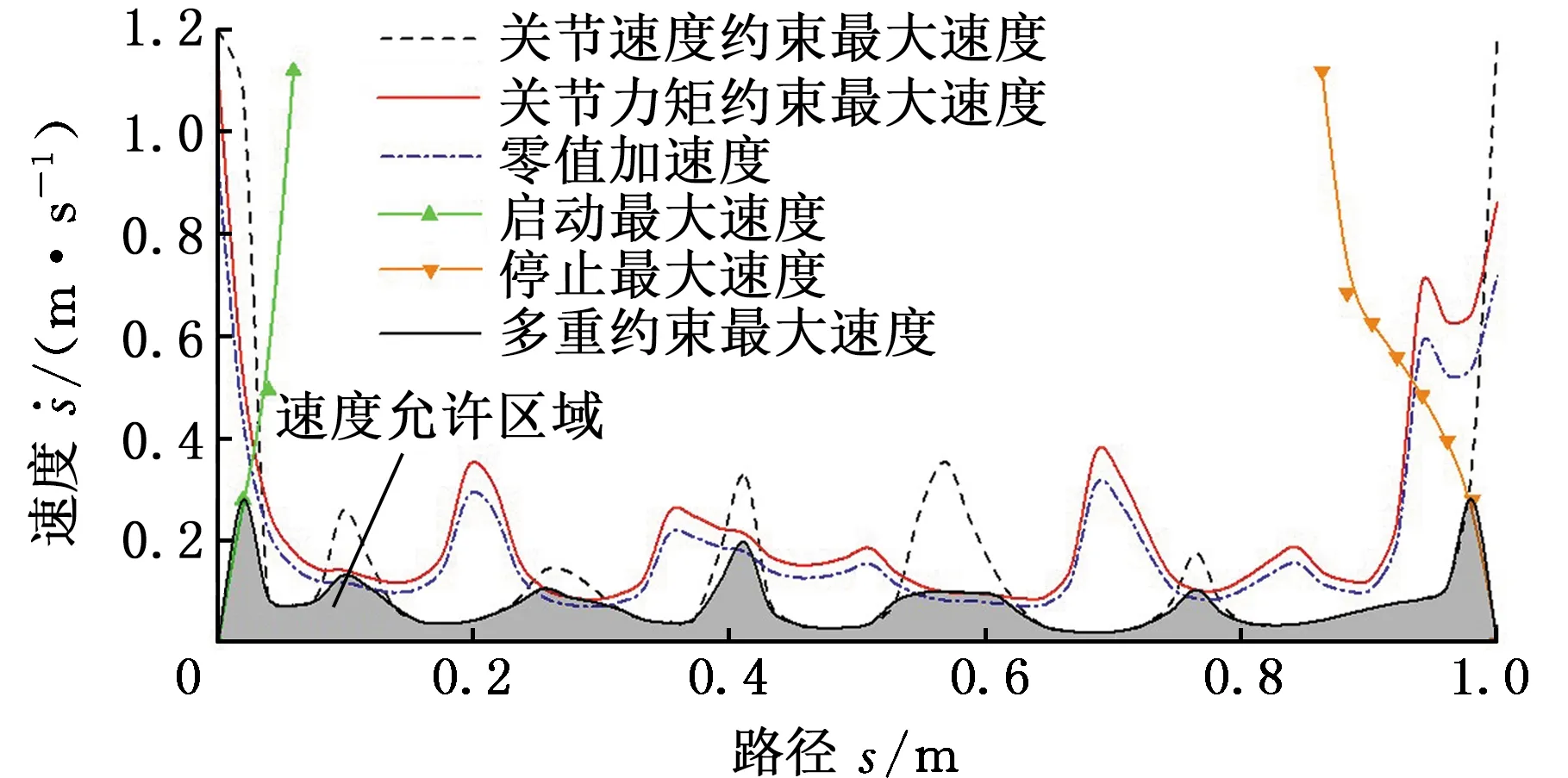
图17 复杂目标轨迹相平面

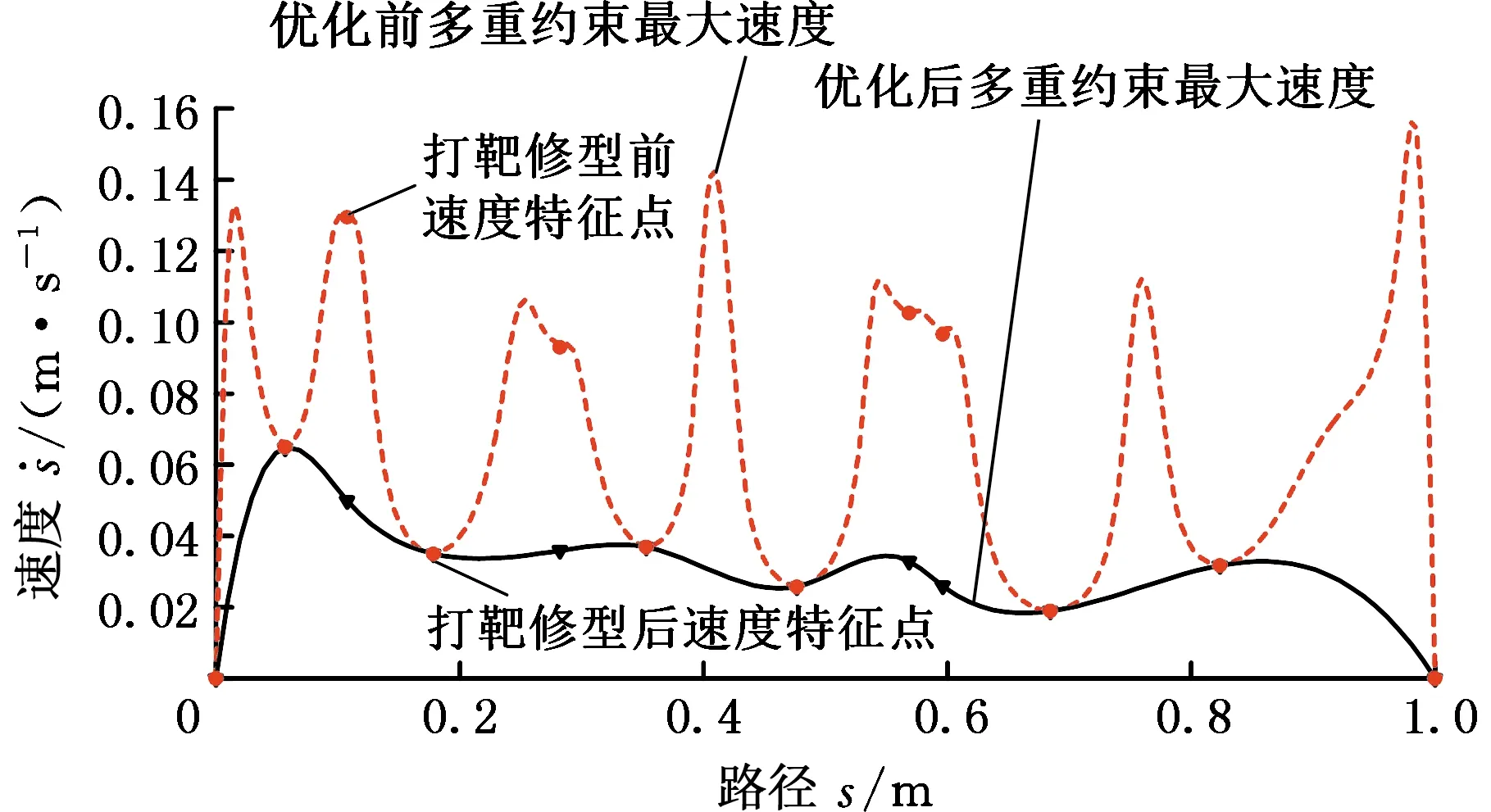
图18 修正后复杂目标轨迹相平面 phase plan of complex trajectory after correction

4.2 算法计算效率分析

4.2.1路径特征点数目对算法计算效率的影响

合适数目的路径特征点序列将影响轨迹规划算法的计算效率与有效性。当不采用路径特征点算法时路径特征点序列为依次经过的路径点，与路径复杂程度、机械臂非线性程度无关。路径特征点算法以路径的复杂程度、机械臂非线性程度为评价变量，模糊计算路径特征点间距ds∈(0,1)，再等间距提取路径特征点，与目标轨迹路径点数目无关。图19所示为采用路径特征点算法与不采用路径特征点算法对复杂目标轨迹进行规划的计算耗时，从中不难看出，路径点数目越多，算法越耗时，当路径点数目过多时，采用路径特征点算法将大幅提高轨迹规划算法的计算效率。

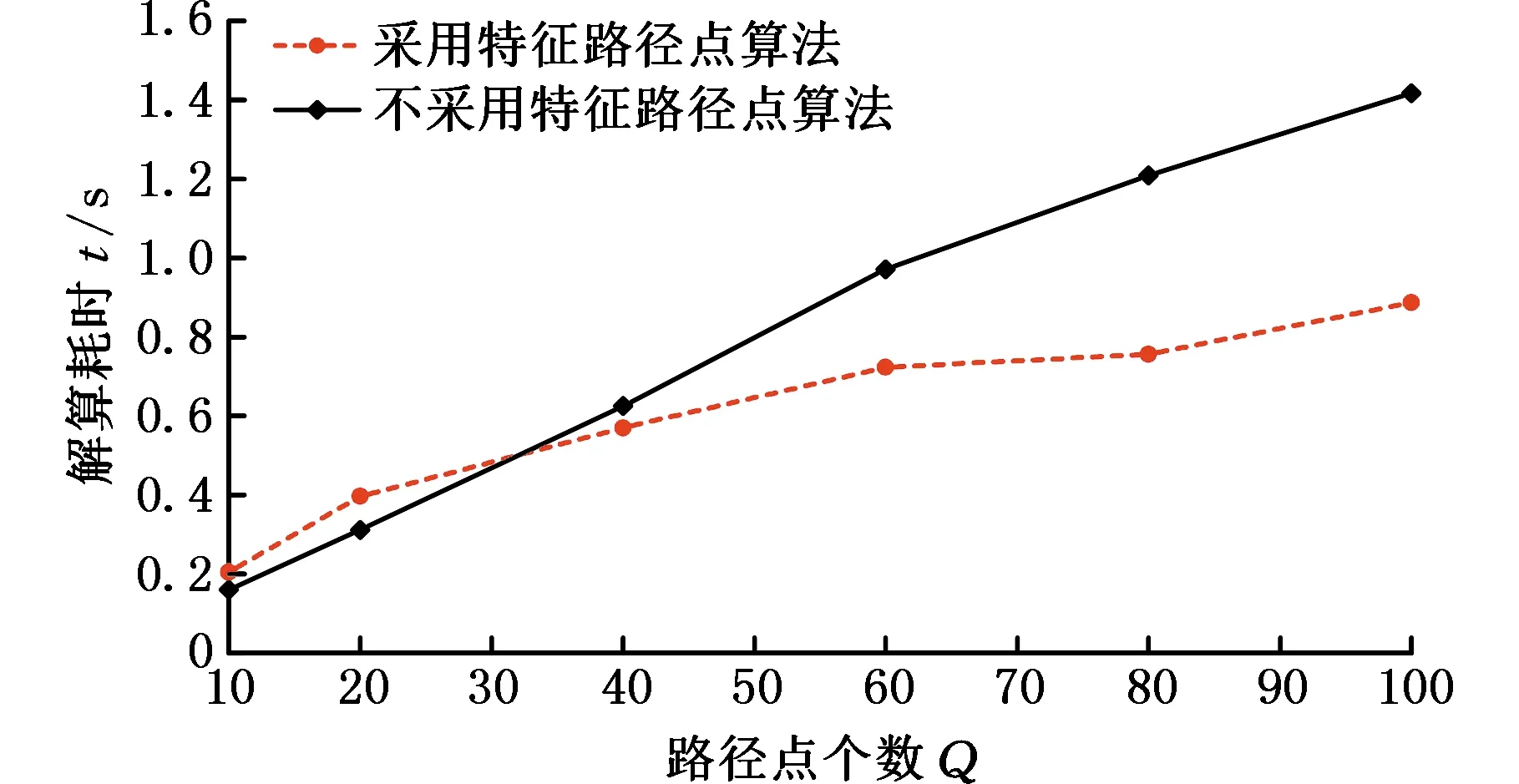
图19 路径离散点数目对算法效率的影响

速度曲线规划算法可分为如下几步：连续路径轨迹的生成及路径特征点的获取T1、获取多重约束最大速度曲线T2、最大速度曲线的优化T3。表2所示为轨迹规划算法优化前后，对简单目标轨迹与复杂目标轨迹进行规划各步骤所占解算时间的比例，不难看出，优化前获取多重约束最大速度曲线T2为轨迹规划算法的主要计算时间，并且它在复杂目标轨迹规划中所占用的比例大于简单目标轨迹，优化后，获取多重约束最大速度曲线T2的占比大幅度缩小。因此采用加速度恒为0的速度曲线替代最大速度曲线V2，可极大地缩短轨迹规划的耗时。

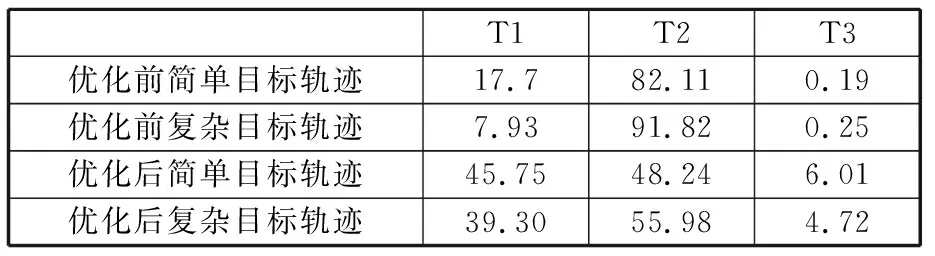
表2 轨迹规划算法各步骤计算时间占比

4.2.2不同轨迹规划算法/优化算法的计算效率

在实际应用中，采用轨迹规划算法/优化算法规划目标路径轨迹的速度曲线所花费的时间是衡量轨迹规划算法计算效率的重要标准。为了研究本文轨迹规划算法相对于其他轨迹规划算法/优化算法的性能，对比分析速度曲线规划算法、遗传算法[7-8]、凸优化算法[3,9]对简单轨迹、复杂轨迹的计算效率，结果如表3所示。不难看出，本文轨迹规划算法相对于其他两种路径规划算法计算耗时最少，遗传算法耗时最多，此外复杂轨迹的计算耗时长于简单轨迹的计算耗时。

表3 优化算法计算效率对比表

综上所述，速度曲线规划算法相对于凸优化算法、遗传算法在计算效率上具有一定的优势，路径的复杂程度影响轨迹规划算法的计算效率，路径越复杂，相应规划用时也越长；此外路径点的数目对规划算法影响最大，过多的路径点将降低轨迹规划的效率，但本文采用的路径特征点法与速度特征点法可在一定程度上降低路径特征点数目对速度曲线规划算法计算效率的影响。

5 结论

本文的轨迹规划算法以相平面法为基础，并对相平面法进行优化，以提高算法的计算效率及保证规划的轨迹连续光滑。

(1)算法计算效率的提高。通过模糊推理计算路径点数目来减小计算规模；采用加速度恒为0的速度曲线替代最大速度曲线V2，简化最大速度曲线V2的求解，缩短计算时间。

(2)速度曲线连续光滑处理。通过速度特征点法提取多重约束最大速度曲线的速度特征点，再通过B样条插值法对速度特征点进行插值，保证速度曲线连续光滑；采用修型-射靶算法对速度曲线进行修形，使得到的速度曲线满足约束要求。

最后通过实验验证了本文轨迹规划算法对不同复杂程度目标轨迹的有效性，目标轨迹的复杂程度越大，其计算时间越长，此外验证了其计算效率与路径特征点数目成正相关。通过对比验证了本文轨迹规划算法相对于凸优化算法、遗传算法具有更高的计算效率。