再谈功的概念

曾浩生 何思芳

(湖南师范大学物理与电子科学学院 湖南 长沙 410081)

1 引言

在讨论功的概念时，几乎所有教科书都给出相同的数学公式A=Fscosα.但对其中位移“s”的理解不尽相同，有理解为“物体的位移” “力的作用点的位移” “受力质点的位移”， 等等.需要指出的是，功的概念一般都是在质点力学中给出的.当受力对象为质点时，上述说法都是正确的.而当受力对象有一定的大小和形状，不能看作是质点时，上述说法的含义不尽相同，于是就出现了争议和误解[1～6].事实上，对于非质点体系，上述任何一种说法都不能完全正确地给出功的定义.鉴于问题的重要性，而且始终没有得到完美地解决，有必要再次进行讨论.我们发现，当受力对象为刚体时，运用作用在刚体上的力的性质，能够完美地理解功的计算，澄清在功的计算过程中时常产生的困惑和错误.

2 作用在刚体上的力的性质

作用在刚体上的力对刚体产生两种效果：一是使刚体的质心产生平动；二是使刚体绕过质心的轴做加速转动.从这两种效果出发，可以推出作用在刚体上的力满足如下两条性质：

(1)力的滑移定理.作用在刚体上的力是滑移矢量.作用在刚体上的力可以沿力的作用线滑移而不改变力的作用效果.或者说，作用在刚体上的力的三要素为力的大小、方向和作用线.

(2)力的平移定理.作用在刚体上的力可以平移到另一点，同时附加一力偶矩的作用.

如图1所示，一力F作用在刚体上的A点，在B点加一零力系(F′,F″),满足F′=F″，于是力F的作用就等价于F′再加上力偶矩(F,F″)的作用.附加力偶矩的大小M=Fd(d为力平移的距离)，方向垂直向里.

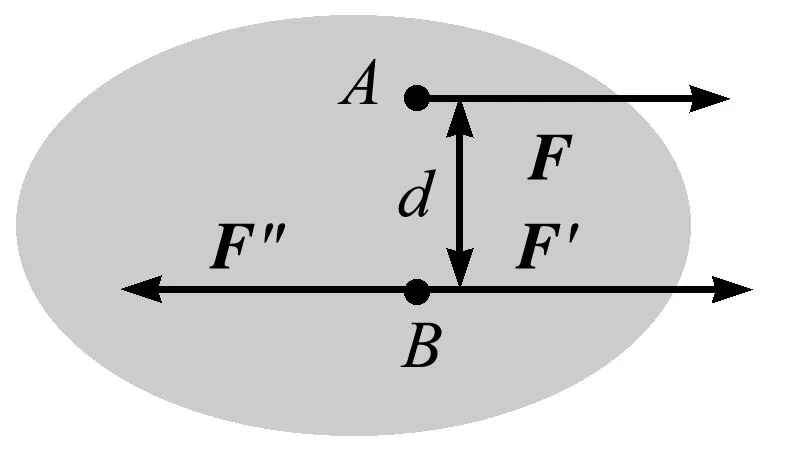
图1 阐述力的平移性质示意图

3 作用在刚体上的力所做的功

刚体的运动可分为平动、转动，以及它们的复合运动.我们将分这3种情况讨论功的计算.

3.1 刚体平动时功的计算

【例1】如图2所示，一卡车载有质量为m的木箱，在平直的公路上行使，因紧急情况突然刹车.刹车后卡车向前滑行了L的距离后静止，木箱在卡车上相对于卡车滑行了l的距离后静止在卡车上.设木箱与卡车间的滑动摩擦系数为μ，试计算木箱与卡车之间的摩擦力对卡车所做的功.

此题中木箱对卡车的摩擦力作用点在不断地变更，在计算功时，位移到底是L，还是L+l？不好确定.但如果采用刚体模型，将卡车视为刚体，利用力的滑移性质，将木箱对卡车的摩擦力滑移到卡车的质心，由于卡车质心所发生的位移为L，于是木箱对卡车的摩擦力所做的功为A=μmgL，问题变得十分清晰.

图2 行驶中的卡车，当木箱在卡车上滑动时， 计算木箱对卡车的摩擦力做功示意图

【例2】如图3所示，手持一支钢笔，钢笔在重力作用下顺势下滑h高度，设手与钢笔之间的滑动摩擦力为f，研究手对钢笔的摩擦力所做的功.

图3 钢笔在手中滑落时，计算手对钢笔的摩擦力做功示意图

如果按照质点力学中功的定义，手对钢笔的摩擦力，其作用点在不断地变更，但当质点受力时没有位移，质点发生位移时没有受力，从而得出手对钢笔的摩擦力不做功的错误结果.但若采用刚体模型，根据力的滑移定理，将钢笔所受摩擦力滑移到钢笔的质心，而质心所发生的位移为h，故得功A=-fh，十分清楚地给出正确结果.

3.2 刚体定轴转动时功的计算

先简单回顾一下力矩做功的概念.如图4所示，圆盘半径为r，在水平力F的作用下绕其中心轴转动.若力F始终作用在圆盘边沿的某一固定位置，并且沿圆盘大圆的切线方向，按照质点力学中功的概念，力F所做的功为

即力F的功等于其对转动轴的力矩的功.如果按照刚体力学的观念，根据平移定理，将力F平移到圆盘中心O，同时附加一力偶矩M=Fr的作用.由于圆盘中心不发生位移，平移到圆盘中心的力对圆盘不做功.而附加力偶矩所做的功等于

这就是力矩做功的来历.

图4 阐述力矩做功示意图

【例3】如图5所示，砂轮半径为r，以ω的角速度绕其中心轴转动.设边沿处被打磨的物体与砂轮间的滑动摩擦力为f，求当砂轮转过角度Θ时，摩擦力对砂轮所做的功(设被打磨的物体相对于地面静止).

图5 打磨物体时，计算摩擦力对砂轮做功示意图

此题中，物体对砂轮的摩擦力的作用点在不断地更换，当质点受力时没有位移，发生位移时不受力，按照质点力学中功的概念，同样得出摩擦力对砂轮不做功的错误结果.如果采用刚体力学的观点，根据力的平移定理，将摩擦力平移到砂轮质心处，再加上力偶矩M=fr的作用.由于砂轮质心不发生位移，作用在砂轮质心处的力不做功.附加力偶矩做功为

此时也就是摩擦力对砂轮所做的功.若f为恒力，则

A=-frΘ

3.3 刚体做一般运动时功的计算

当刚体做平动与转动的复合运动时，要计算作用在刚体上的某个力F所做的功，我们同样可以利用力的滑移定理与平移定理，将力移到刚体的质心.此时平移到刚体上的力可能会做功，于是，力F所做的功等于移到刚体质心处的力所做的功与附加力偶矩所做的功之和.

【例4】一汽车在笔直的公路上行驶，假定车轮相对地面不打滑，研究地面对车轮的静摩擦力所做的功.

若采用质点力学的观点，车轮所受的静摩擦力作用点在不断地变更，但质点受力时不发生位移，故地面对车轮的静摩擦力不做功.若采用刚体模型，我们可以将地面对车轮的静摩擦力f平移到车轮的质心，同时附加一力偶矩M=fR(R为车轮的半径).设汽车前进的距离为s，则平移到车轮质心处的力所做的功

A1=fs

而附加力偶矩所做的功

A2=-Mθ=-fs

故总功

A=A1+A2=0

两种理解结果一致.

【例5】如图6所示，半径为R的圆柱体在重力作用下沿斜面连滚带滑地从顶端运动到底端，设斜面的长为L，斜面对圆柱体的滑动摩擦力为f，试研究下滑过程中滑动摩擦力对圆柱体所做的功.

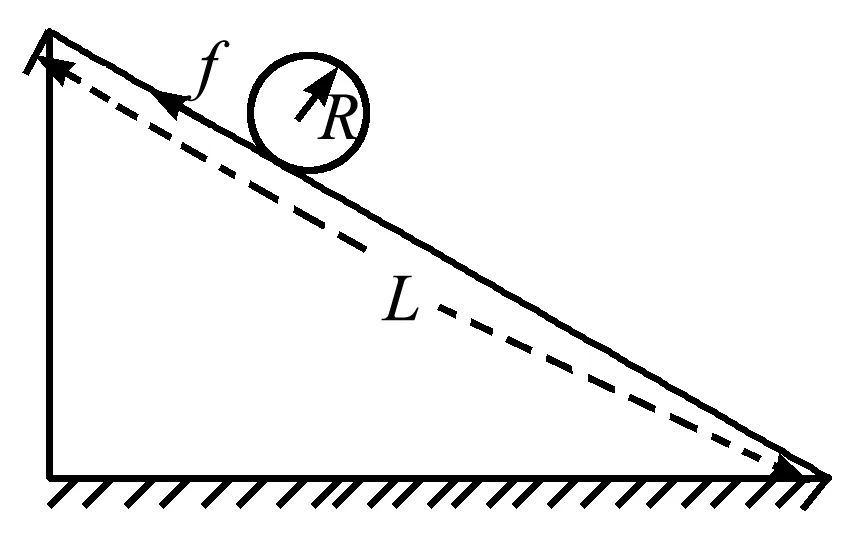
图6 圆柱体在斜面上有滑动地滚下， 计算摩擦力对圆柱体做功示意图

此题中，圆柱体所受的摩擦力的作用点同样在不断地更换，按质点力学中功的概念很难求得正确结果.若采用刚体模型，问题将变得十分清楚.将摩擦力f平移到圆柱体的中心，同时附加力偶矩M=fR的作用.平移到圆柱体中心的力f在运动过程中所做的功显然等于-fL.然而，附加力偶矩在运动过程中也要做功.设在运动过程中圆柱体转过的角度为θ(由于有滑动，应有θR

A=-fL+fRθ<0

4 总结

总之，质点力学中所定义的功的概念原则上只适用于受力对象为质点的情况，不能随意地推广应用到受力对象为非质点的情况，否则就会产生困惑甚至错误.例如，若采用“力的作用点的位移”或“受力质点的位移”，就很难正确地理解例题1～3和例题5中功的计算；若采用“物体的位移”，就很难计算例题3～5涉及的功.但如果采用本文所述的刚体模型的概念，问题就会变得十分清楚和容易解决.