基于GNSS的风电机组低频振动位移计算方法研究*

王 潇,俞佳男,唐 波,余清清,许国东

(浙江运达风电股份有限公司 浙江省风力发电技术重点实验室,浙江 杭州 310012)

0 引 言

随着风电行业的发展,对风能的利用率要求越来越高,风电机组的塔架也越建越高,叶轮和塔架发生耦合振动的临界风速也越来越低,由此引起的整机低频振动问题日益严峻。长期的低频振动会造成叶片、塔架、传动链部件和机电设备的故障和失效破坏,这不仅带来了维修更换的经济损失,严重时还会导致风电机组的安全事故。

目前,对风电机组的振动监测大多通过加速度传感器来实现。但在实际测试和计算过程中,传统加速度传感器对低频振动不敏感,长期监测还会出现零漂和温漂,加速度二次积分计算位移的算法会引入较大误差,所以寻找可靠的风电机组低频振动位移计算方法尤为重要。

目前,风电机组在线状态监测[1]是数字化、智能化风电技术发展的趋势和需求,振动监测主要通过加速度传感器进行特征信号记录和故障诊断分析[2-4]。对于风电机组的低频振动位移,卓沛骏等[5]利用倾角传感器测量了塔顶转角数据,并通过Bladed软件仿真获取了不同风速下塔顶位移与转角的线性关系,进而实现了塔顶转角到位移的转换;但该方法需要通过仿真模型计算转换关系,与实际情况存在一定的偏差。BANG等[6]将光纤光栅应变片粘贴到塔筒不同高度处,实时获取塔筒的变形挠曲线,从而计算塔顶位移;但该方法成本较高、操作困难。ZENDEHBAD等[7]提出了利用激光测振的方法测试风电机组塔顶位移;该方法虽然操作方便且精度高,但设备成本较高,不适合长期监测。

随着GNSS(global navigation satellite systems)技术的发展,其定位精度能够达到毫米级,国内很多专家将其应用在建筑高塔、桥梁等的变形和安全监测上[8-13],并开展了深入研究。在国外,TAMURA等[14]考虑了加速度传感器无法准确获取建筑物风致振动响应的动态波动分量,利用RTK-GPS技术对其进行了测量分析。BREUER等[15]利用GNSS技术对弱风条件下高层结构位移进行了测量。PIOTR[16]对GNSS技术在高烟囱水平动态位移计算中的局限性进行了分析。

本文将GNSS技术引入到风电机组的低频振动监测,提出一种基于GNSS-RTK精准定位技术的风电机组机舱低频振动位移计算方法;通过构建风电机组机舱空间运行轨迹模型,利用该方法对仿真模型进行解算,并与仿真设定的位移作对比分析;在现场测试中,同时布置GNSS设备和加速度传感器设备,并将它们的位移结果与Bladed软件计算的理论位移作趋势和误差分析,进而从仿真计算和现场测试两方面验证本方法的正确性和准确度。

1 计算方法

笔者在风电机组运行空间中建立三维直角坐标系,X轴和Y轴表示水平面两个方向,与移动站天线的坐标方向一致,Z轴表示风电机组的高度方向,风电机组低频振动位移计算模型如图1所示。

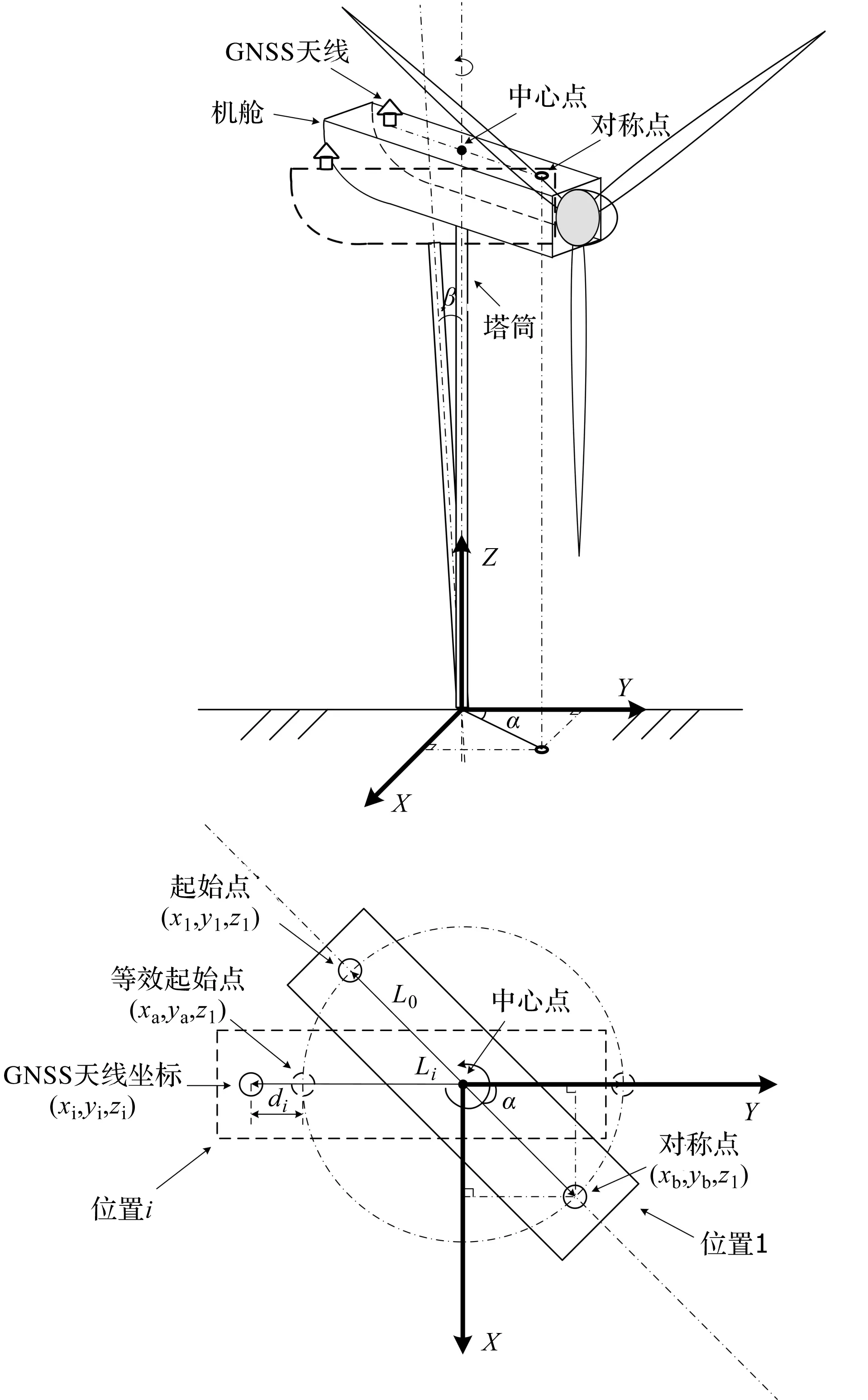
图1 风电机组低频振动位移计算模型

下面,笔者具体介绍单天线定位坐标解算风电机组机舱低频振动位移的方法。

1.1 基准设定

以风电机组无风状态下的位置为基准,设定水平面内塔筒中心点Z方向上投影到机舱顶部的点为理论计算中心点(x0,y0,z0)。由于塔筒是标准的圆形结构,笔者在塔筒外壁采用三点定圆心的方法测定x0和y0;z0是无风状态下机舱顶部距离地面的垂直距离。

在水平面内,以小风停机状态下GNSS移动站天线的坐标(x1,y1,z1)为起始点,其相对于中心点的对称点坐标为(xb,yb,z1)。当风电机组运行时,机舱会发生偏航和摆振的复合运动(如图1所示),移动站天线从位置1运动到位置i,GNSS接收机记录移动站天线坐标为(xi,yi,zi);在水平面内,起始点(x1,y1,z1)以中心点(x0,y0,z0)为圆心旋转到位置i处的等效坐标为(xa,ya,z1),移动站天线起始点坐标满足x1=xa,y1=ya。

1.2 位移计算

基于GNSS的机舱低频振动位移的计算,都是相对于机舱运动后等效的起始点坐标(xa,ya,z1),定义位移为di。

在水平面内,起始点到中心点的距离L0/2可表示为:

(1)

当风电机组运行时,移动站天线在位置i处的空间坐标为(xi,yi,zi),其中i=1,2,3…。

在水平面内,移动站天线与Y轴的夹角α为:

(2)

这里反正切函数的取值范围是[-π/2,π/2],但风电机组运行时,移动站天线与Y轴正方向的夹角为α+会出现在[0,2π]范围内,可表示如下:

(3)

机舱运动后等效的起始点坐标可以表示为(xa,ya,z1),其中,xa和ya的计算式为:

(4)

(5)

通过移动站天线坐标(xi,yi,zi)和等效起始点坐标(xa,ya,z1),可以计算得到机舱低频振动的位移di,即:

(6)

将式(4，5)代入式(6),可得位移di的具体表达式为:

其中,i=1,2,3…。

(7)

1.3 方向判定

由式(6)可知,机舱低频振动计算的位移值均为绝对值,无法反映机舱振动的前后方向,故本文计划通过特定的位移条件来判定,并给相应的位移值添加正负号来表示机舱低频振动位移的方向。

此处以机舱朝着叶轮方向的运动为位移计算的正方向,反之为负方向。

机组运行到位置i时等效起始点为(xa,ya,z1),在水平面内等效起始点相对于中心点(x0,y0,z0)的对称点为(xb,yb,z1),通过坐标变换可表示为:

xb=2x0-xa

(8)

yb=2y0-ya

(9)

当机组运行到位置i,移动站天线坐标(xi,yi,zi)到对称点(xb,yb,z1)的距离为Li,其计算式如下:

(10)

等效起始点(xa,ya,z1)到对称点(xb,yb,z1)的距离为L0,其计算式如下:

(11)

将式(4,5,8,9)代入式(10)中,可得其具体表达式为:

(12)

结合式(10,11),机舱低频振动位移的方向判断条件可表示如下:

(13)

综上所述,笔者介绍了基于GNSS-RTK精准定位技术的风电机组机舱低频振动位移计算方法,其流程如图2所示。

图2 风电机组低频振动位移计算方法流程图

2 仿真验证

针对上述的风电机组机舱低频振动位移的计算方法,笔者开展理论仿真验证。

首先,笔者搭建风电机组运行时GNSS移动站天线空间轨迹模型;然后,利用上述建立的低频振动位移计算方法得到风电机组机舱的低频振动位移;最后,将仿真计算得到的机舱低频振动位移与仿真模型中的理论位移作对比分析,计算它们之间的偏差。

GNSS移动站天线空间运行轨迹如图3所示。

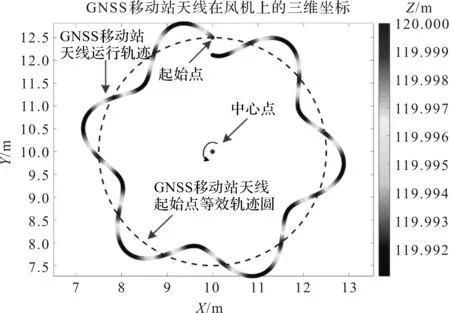
图3 GNSS移动站天线空间运行轨迹

在图3中,设定中心点坐标为(10,10),GNSS移动站起始点到中心点的水平距离为2.5 m,到地面的垂直高度为120 m,渐变线带为GNSS移动站天线的运行轨迹,虚线圆表示GNSS移动站起始点的等效轨迹圆。

该仿真研究中,风电机组一边作逆时针的偏航运动,一边沿着机舱前后方向作摆振运动,机舱最大摆动位移设为0.4 m,摆振频率设为0.2 Hz。因此,GNSS移动站运行轨迹沿着虚线前后作简谐振动,并沿着逆时针方向作旋转运动。另外,云图颜色表示GNSS移动站天线垂直高度的变化。

笔者利用上述低频振动位移计算方法,对仿真模型中风电机组机舱低频振动位移进行计算,结果如图4所示。

图4 风电机组低频振动位移仿真计算结果

由图4可知,仿真计算得到的机舱低频振动位移是幅值为0.4 m,频率为0.2 Hz的简谐振动,与仿真模型设计的结果一致;将仿真计算得到的低频振动结果与仿真模型中机舱前后振动的理论位移作对比分析,得到它们之间偏差在10-15数量级。

通过以上的仿真计算结果,验证了笔者提出的基于GNSS的风电机组低频振动位移计算方法的正确性。

3 现场测试

3.1 测试设备

针对该方法的现场测试在某风场进行。现场的测试风机和使用设备的详细参数如表1所示。

表1 现场测试风机和主要设备参数表

3.2 设备布置

在测试过程中,主要包括两套设备的现场布置,分别是GNSS设备和低频加速度设备。其中,GNSS设备分为基准站和移动站,基准站包括了CR3-G3天线、GNSS接收机和外置电台,整体布置在空旷的地面上;移动站包括了CR2天线和GNSS接收机,布置在风电机组机舱顶部靠后端的吊耳处。

GNSS基准站现场布置图如图5所示。

图5 GNSS基准站现场布置图

为了保证移动站尽可能水平和稳固的布置于机舱顶部,笔者设计了特定的固定装置,加速度传感器通过磁吸式的方式布置在固定装置的肋板上,与机舱前后振动方向一致。

GNSS移动站和加速度传感器现场布置图如图6所示。

图6 GNSS移动站和加速度传感器现场布置图

3.3 数据采集

对于GNSS设备,测试前需对基准站和移动站进行参数配置,并保证移动站与基准站经电台保持有效通讯,当移动站配置界面的解状态显示为固定解,差分延时小于5,说明移动站接收机的采集结果有效。

加速度传感器通过LEMO接口与数据采集仪连接,采样频率为100 Hz。另外,实际测试前需对GNSS设备和加速度数据采集仪进行对时,保证两套设备的北京时间一致,方便后续数据分析。

4 数据计算与分析

通过SCADA导出现场测试时的风速,笔者利用Bladed软件,计算得到测试风速下机舱的理论位移,并与加速度传感器设备和GNSS设备的计算结果作趋势分析和误差分析。

4.1 趋势分析

笔者选取18:34:25至18:38:47时间段的数据进行计算和分析,并对SCADA导出风速、加速度数据和GNSS接收机采集数据进行截取;通过Bladed软件计算风电机组机舱的理论位移;利用高阶逼近的方法,对理论位移曲线进行拟合，反映了理论位移的变化趋势。

Bladed软件计算的理论位移和其拟合曲线如图7所示。

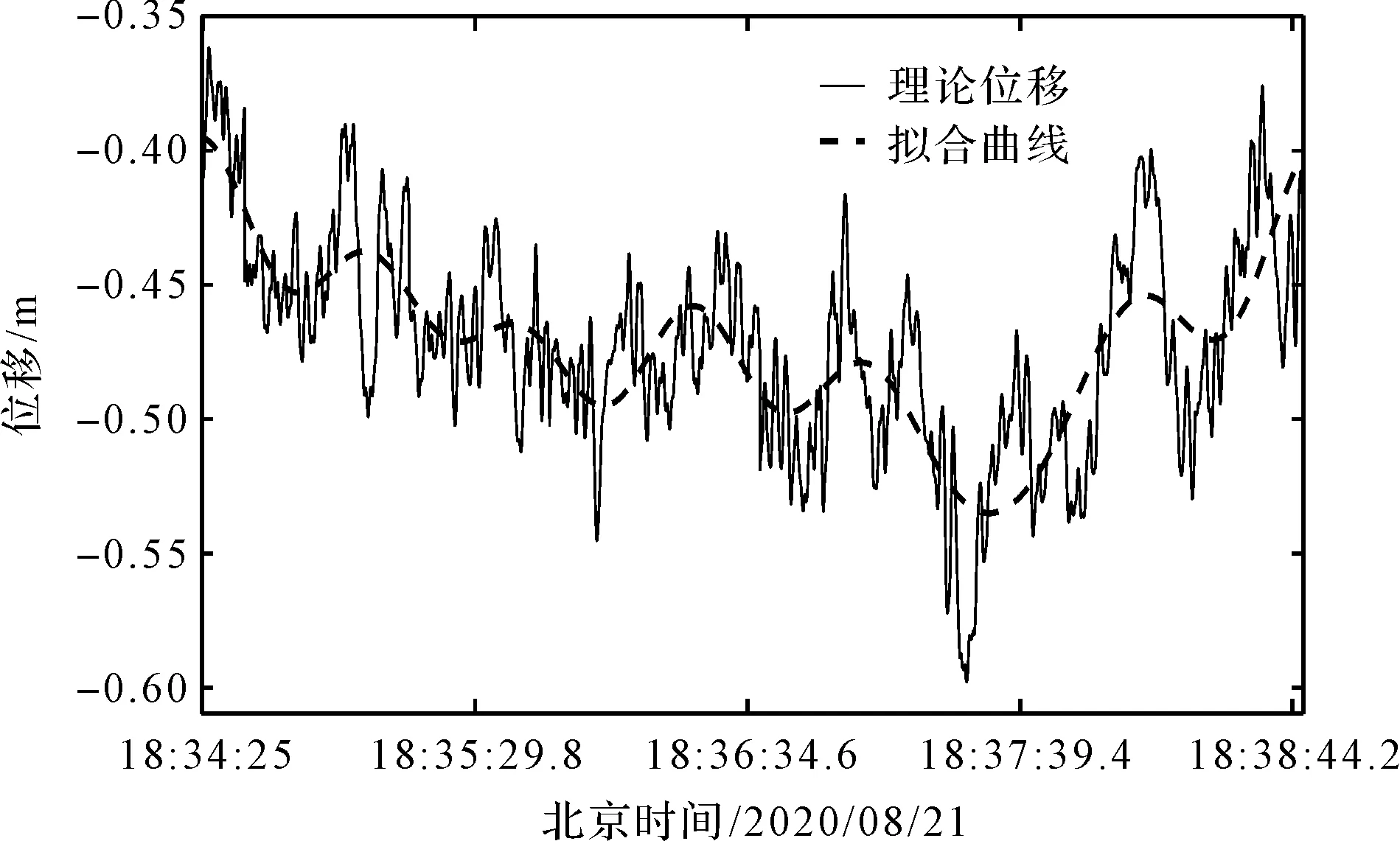
图7 Bladed软件计算的理论位移和其拟合曲线

依据所提出的风电机组机舱低频振动位移计算方法,笔者对GNSS设备采集数据进行计算和分析,得到实测的机舱低频振动位移;同样,利用高阶逼近的方法对位移曲线进行拟合,该拟合曲线反映了基于GNSS实测数据计算位移的变化趋势。

基于GNSS的机舱低频振动位移和其拟合曲线如图8所示。

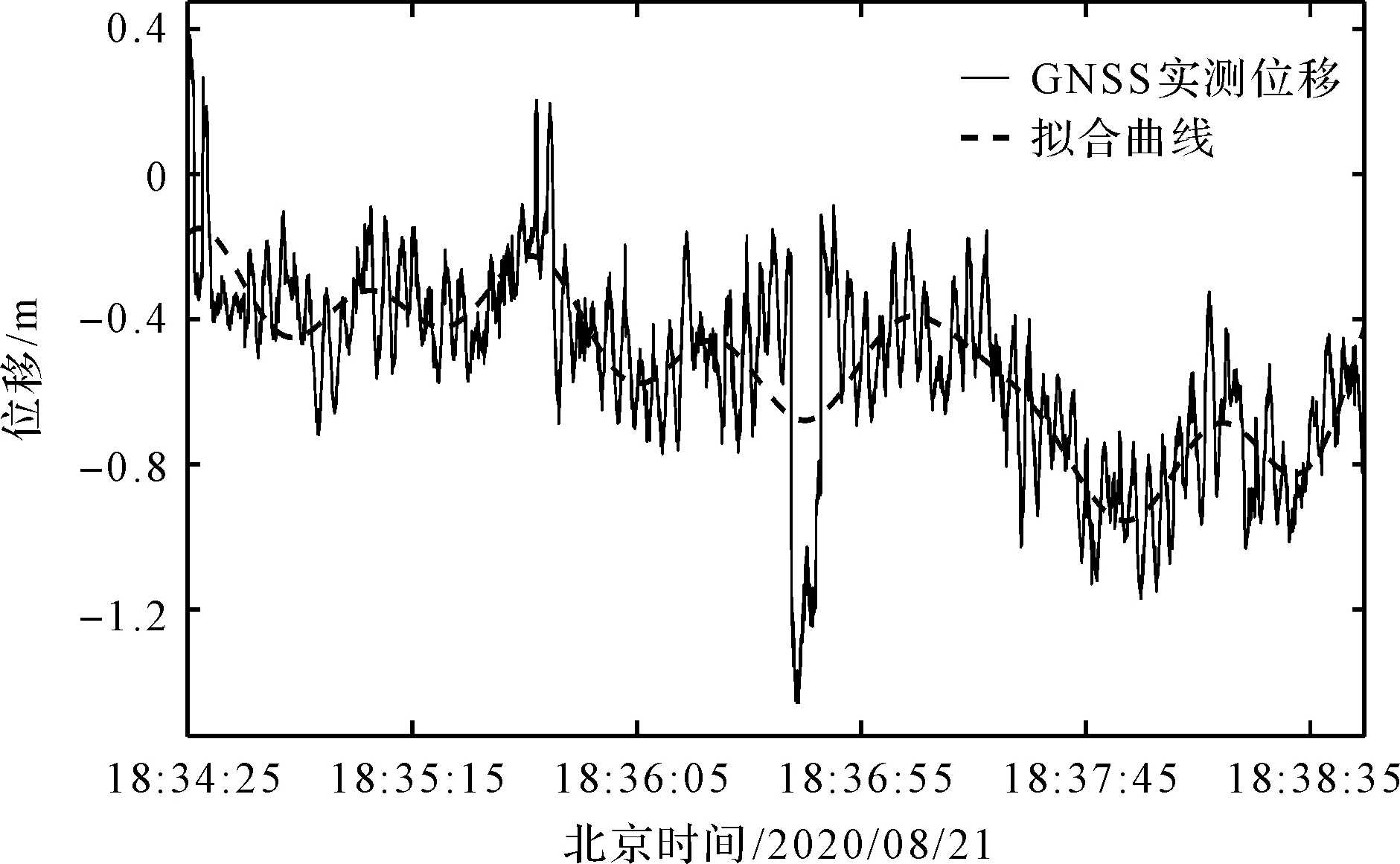
图8 基于GNSS的机舱低频振动位移和其拟合曲线

由于风电机组机舱的低频振动频率在0.2 Hz左右,笔者对加速度信号进行滤波处理,得到只包含低频振动成份的加速度信号;接着,又对其进行二次积分,得到其位移。

加速度传感器设备计算位移如图9所示。

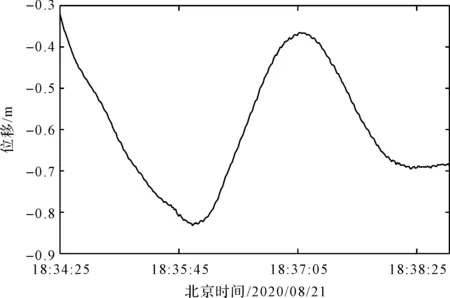
图9 加速度传感器设备计算位移

对比图(7,8)可知,理论位移和基于GNSS实测数据计算的机舱低频振动位移的结果范围相近,均在0.45 m附近;另外,它们的拟合曲线相似,一致性较好,表明理论位移和该方法计算位移的变化趋势一致,进一步验证了基于GNSS的风电机组低频振动位移计算方法的正确性。

然而,在加速度计算位移的方法中,滤波处理不仅不能准确地获取低频成分,还会造成高频成分的泄露,两次积分运算会引入计算误差,所以位移曲线中很多细节丢失,位移的变化趋势简单,无法真实地反映风电机组机舱低频振动的情况。

4.2 误差分析

为了进一步验证基于GNSS的风电机组低频振动位移计算方法的准确度,笔者将对理论位移、GNSS设备计算位移和加速度传感器计算位移中,任意10个相同时刻的位移结果进行提取,计算它们的误差。

误差计算式如下:

(14)

式中:Di—某一时刻GNSS设备计算位移,或某一时刻加速度传感器计算位移;di—某一时刻理论位移;i=1,…,N,N=10。

笔者分别在图(7～9)中选取10个相同时刻的位移值,并统计它们对应的测试时间,结果如表2所示。

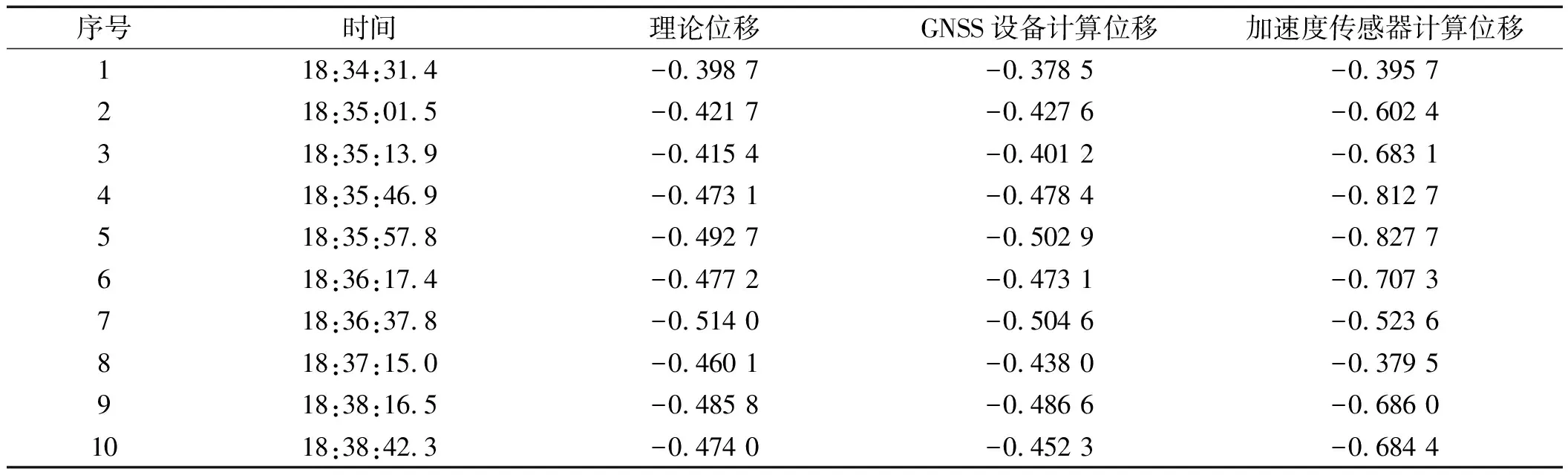
表2 任意10个时刻对应的理论位移和计算位移(单位：m)

笔者利用式(14)对表2的数据进行计算可得,基于GNSS实测数据计算的机舱低频振动位移与理论位移的误差为2.9%,而通过加速度信号二次积分得到的位移与理论位移的误差为47.1%。

以上结果说明,基于GNSS的风电机组低频振动位移计算方法远远优于加速度二次积分计算位移的方法;同时,也从实际工程测试的角度进一步验证了该振动位移计算方法的正确性和准确度。

5 结束语

本文提出了一种基于GNSS-RTK精准定位技术的风电机组机舱低频振动位移计算方法,并从仿真和现场测试的角度对其正确性和准确度进行了验证,得到如下结论:

(1)通过构建机组机舱空间运行轨迹模型,利用本文提出的低频振动位移计算方法对仿真模型进行解算,并与仿真设定的位移值作对比发现,机舱位移作简谐振动的幅值和频率相同,两者的位移偏差在10-15数量级;

(2)利用Bladed软件计算的理论位移与基于GNSS实测数据计算的位移幅值范围相近,均在0.45 m附近,两者的拟合曲线相似,一致性较好,说明了它们的变化趋势一致;而加速度二次积分的位移结果缺少诸多细节,变化趋势简单,无法真实反映风电机组机舱低频振动的情况;

(3)在理论位移、GNSS设备计算位移和加速度传感器计算位移中提取了任意10个相同时刻的位移值,根据计算误差可得,基于GNSS设备计算的位移误差远小于加速度信号二次积分计算位移的误差。

综上所述,不管是仿真研究还是现场测试计算都验证了基于GNSS-RTK精准定位技术的机舱低频振动位移计算方法的正确性和准确度。

另外,该方法精度高、费用成本低,适用于对机组机舱低频振动位移的长期监测。