含间隙曲柄滑块机构的动力学建模及其误差补偿研究*

陈 庆,薛邵文,林乃昌*

(1.泸州职业技术学院 机械工程学院,四川 泸州 646005;2.泸州市智能制造重点实验室,四川 泸州 646005)

0 引 言

机械制造领域中,加工精度、装配公差以及磨损等因素会使各种机构产生运动副间隙[1],导致系统呈现非线性振动,加剧运动副的磨损,降低整个系统的稳定性、可靠性、精度以及使用寿命。因此,含间隙机构的动力学研究成为了智能制造和精密机械领域中亟待解决的问题。

对于含间隙的机构动力学,国内外诸多学者对其已研究多年[2-8]。王见等[9]以3-CPaRR并联机构为研究对象,基于Lankarani-Nikravesh和Coulomb模型,建立了含关节间隙的3-CPaRR并联机构弹性动力学模型,分析了不同的关节间隙对3-CPaRR并联机构运动特性的影响。姜洪奎等[10]基于赫兹弹性接触理论和变形协调原理,考虑了初始游隙和接触角变化等因素,建立了非理想滚道截形的滚珠丝杠副弹性变形接触角的计算模型。何昊南等[11]针对折叠舵面内、外舵铰接处存在的间隙对地面振动响应的影响,及间隙处的非线性建模方法展开了研究。邱雪松等[12]以月球车两级往复可展太阳帆板为研究对象,通过接触碰撞力描述间隙,运用有限元法对太阳帆板进行柔性化处理,建立了多间隙-柔性耦合的动力学模型。侯雨雷等[13]以含转动副间隙RU-RPR并联机构为研究对象,加入Baumgarte违约稳定法和Runge-Kutta法,求解微分代数形式建立的动力学模型,分析了不同摩擦因数对机构动态特性的影响。

在误差补偿方面,孔骏成等[14]在机器人操作手臂模型中,将间隙误差完全等效成杆长误差,利用PSO算法将间隙误差补偿问题转化为求适应度极小值问题。陈纯等[15]建立了Y轴正、反向单向定位精度和反向差值补偿的数学模型,通过840D的丝杠和间隙补偿表功能完成了补偿。唐俊杰等[16]运用了改进的PSO算法,优化了驱动杆位移参数,补偿了由运动副间隙引起的结构误差。吴昊骏等[17]在分析钻孔位姿参数和钻具末端塌落量的函数关系后,对原有车体定位方法进行了修正,对钻孔定位误差进行了补偿。

本文以含间隙曲柄滑块机构为对象,考虑运动副间隙碰撞接触条件及能量耗散因素,结合Nikravesh[18]模型,提出一种表述接触力的非线性弹簧阻尼模型;将其引入到含间隙曲柄滑块机构动力学模型的构建中,分析间隙带来的影响;建立其逆模型,就间隙带来的误差分别进行逆模控制和PID加逆模控制来补偿间隙引起的系统误差。

1 曲柄滑块机构的建模

1.1 理想曲柄滑块机构的建模

曲柄滑块机构示意图如图1所示。

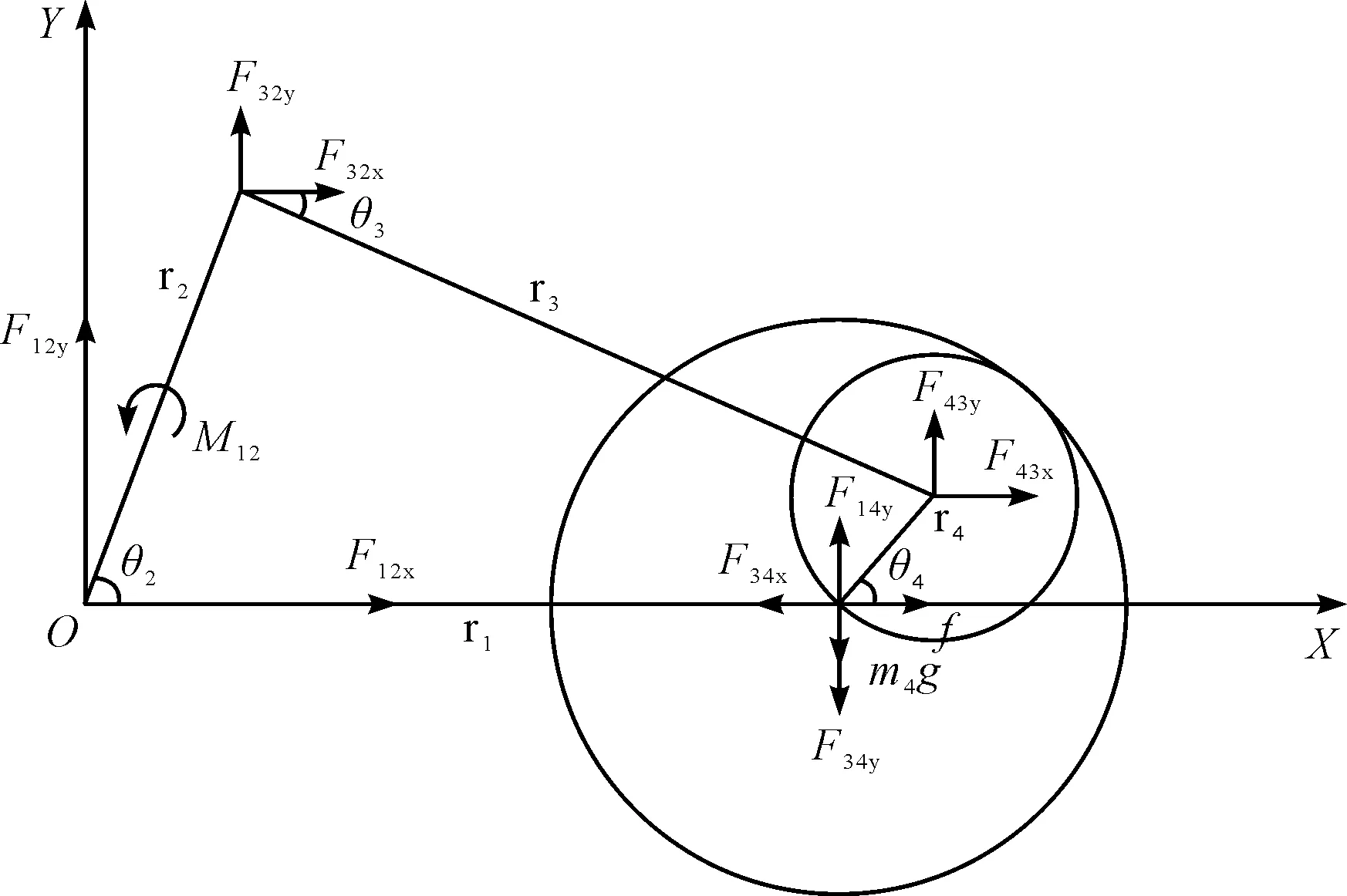
图1 曲柄滑块机构示意图r2—曲柄长度;r3—连杆长度;r1—滑块位移;θ2—曲柄转角;θ3—连杆转角;r4—间隙半径;θ4—x轴与轴销轴套中心连线的夹角;rs1—曲柄质心距o点的长度;rs2—连杆质心距曲柄的长度;m4—滑块质量;M12—曲柄r2转矩;Fmn,x,Fmn,y—机架、曲柄、连杆,滑块两两之间的作用力在x,y轴的分量(其中：m,n=1,2,3,4)

用图1就可表示理想曲柄滑块机构的示意图(忽略其中表示间隙的大圆和小圆)。

由图1可以得到x和y坐标轴的方程式,即:

r2cosθ2+r3cosθ3=r1

(1)

r2sinθ2+r3sinθ3=0

(2)

分别将上述两式对时间求导,分别可得到:

(3)

r2ω2cosθ2+r3ω3cosθ3=0

(4)

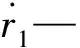
将式(3,4)写成矩阵,即:

(5)

式(5)即为理想曲柄滑块机构的数学模型。

1.2 含间隙曲柄滑块机构的建模

实际系统的间隙:在图1中用大圆和小圆表示连杆轴套与轴销的间隙。

1.2.1 含间隙机构的闭环矢量方程

曲柄滑块机构的闭环矢量方程如下:

R2+R3=R1+R4

(6)

将式(6)分别向x,y轴投影得:

r2cosθ2+r3cosθ3=r1+r4cosθ4

(7)

r2sinθ2+r3sinθ3=r1+r4sinθ4

(8)

将式(7,8)求导可得:

(9)

(10)

1.2.2 含间隙机构的动力学方程

根据图1的受力分析,曲柄动力学方程为:

(11)

式(11)中:

(12)

式中:R—轴销半径。

滑块动力学方程为:

F14,y-Fy-m4g=0

(13)

(14)

1.2.3 接触力的非线性弹簧阻尼模型

本文结合Nikravesh[18]模型,建立表述接触力更精确的非线性弹簧阻尼碰撞模型,即:

(15)

碰撞接触条件取值如表1所示。

表1 碰撞接触条件

该模型综合考虑了接触力是否存在，以及弹性力和碰撞体的材料阻尼引起的能量损失等因素。

接触点轴销相对于轴套的切向速度(Vt)和法向速度(Vn)为:

(16)

(17)

切向触力为:

Ft=(-fsign(Vt)Fn-CtVt)S

(18)

式中:Ct—切向阻尼。

将Fn,Ft向x,y轴分解得:

Fx=Ftsinθ4+Fncosθ4

(19)

Fy=-Ftcosθ4+Fnsinθ4

(20)

最后,联立式(6～20),经整理可得到一个16阶的矩阵,根据矩阵建立的仿真模型如图2所示。

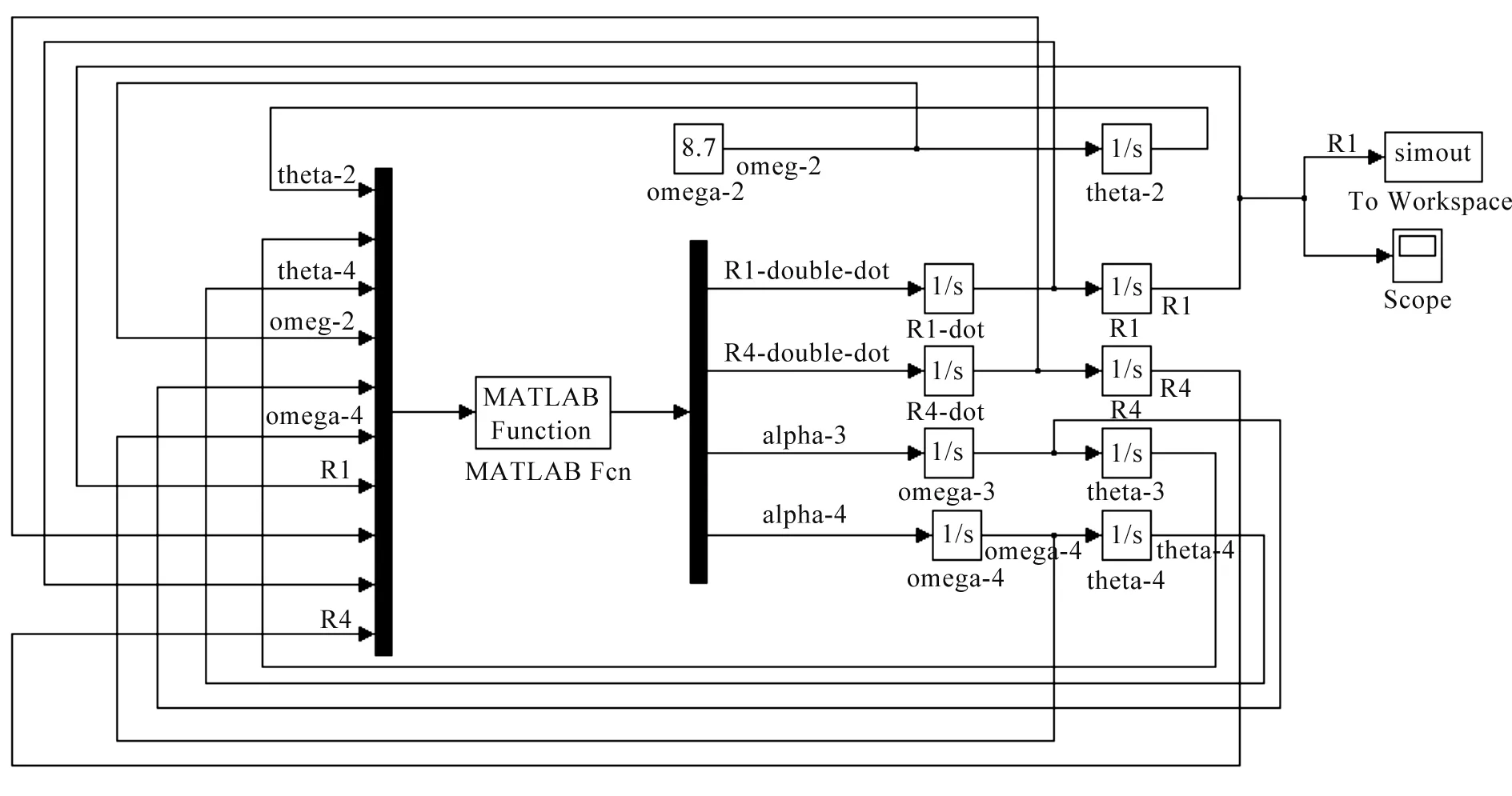
图2 含间隙曲柄滑块机构动力学仿真模型

2 实验验证

2.1 实验平台

为测量曲柄转角,连杆倾角和滑块位移所搭建的实验机构如图3所示。

图3 实验机构

实验平台如图4所示。

图4 实验平台

实验机构的参数如表2所示。

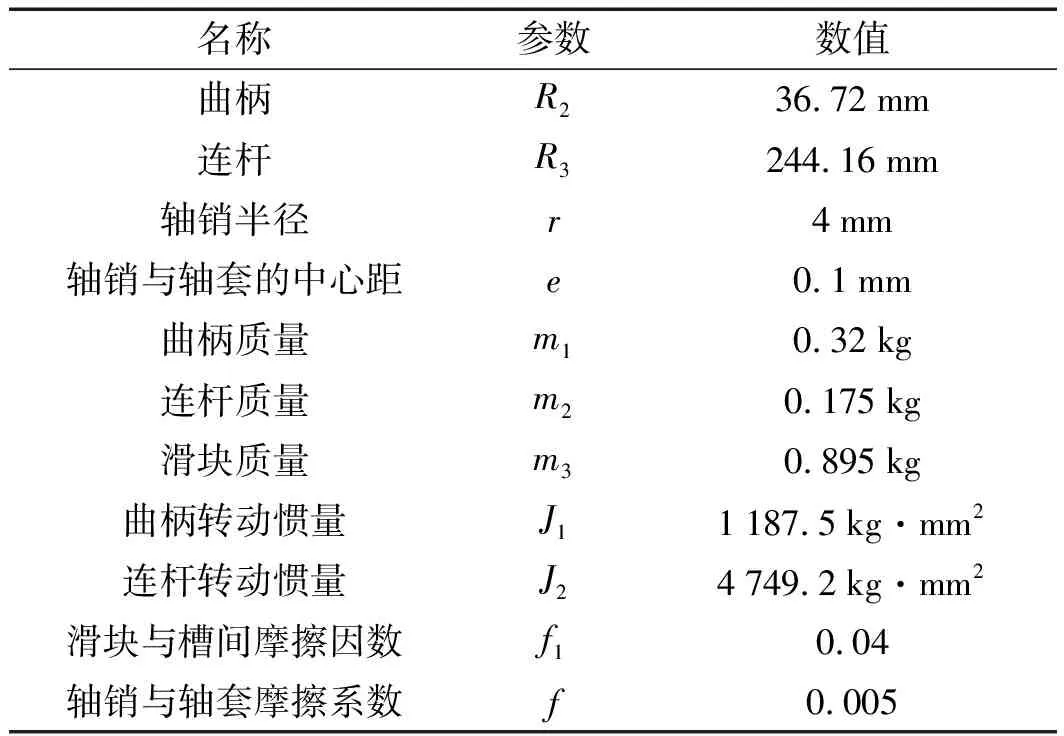
表2 曲柄滑块机构参数

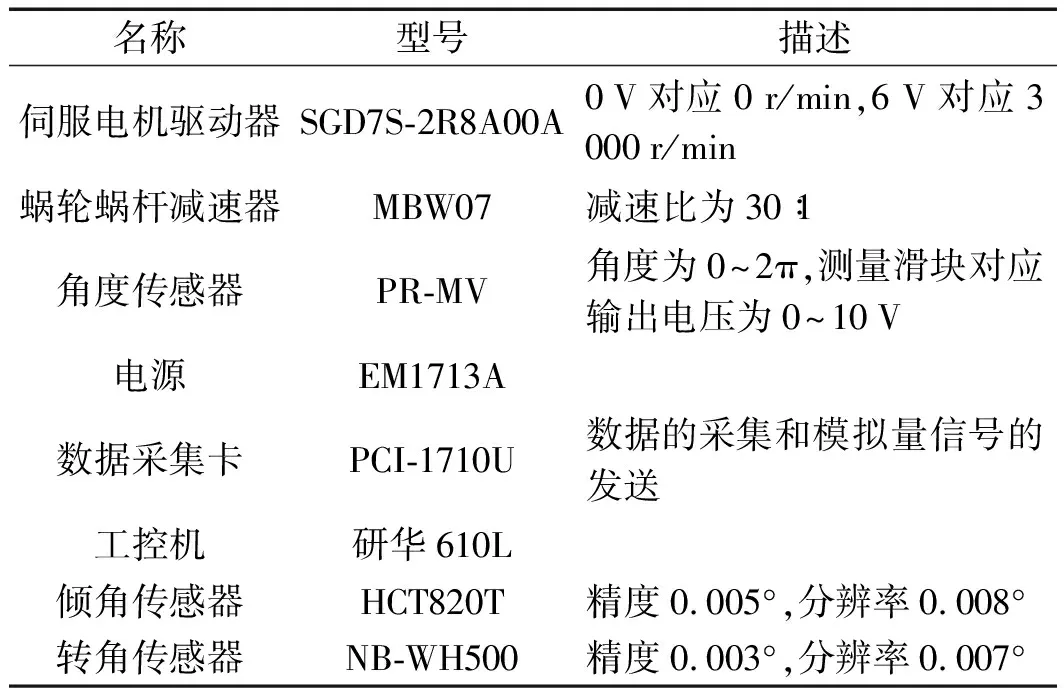
试验平台的规格如表3所示。

表3 实验平台规格

(续表)

2.2 数据采集RTW平台

本次实验所需数据的采集RTW平台如图5所示。

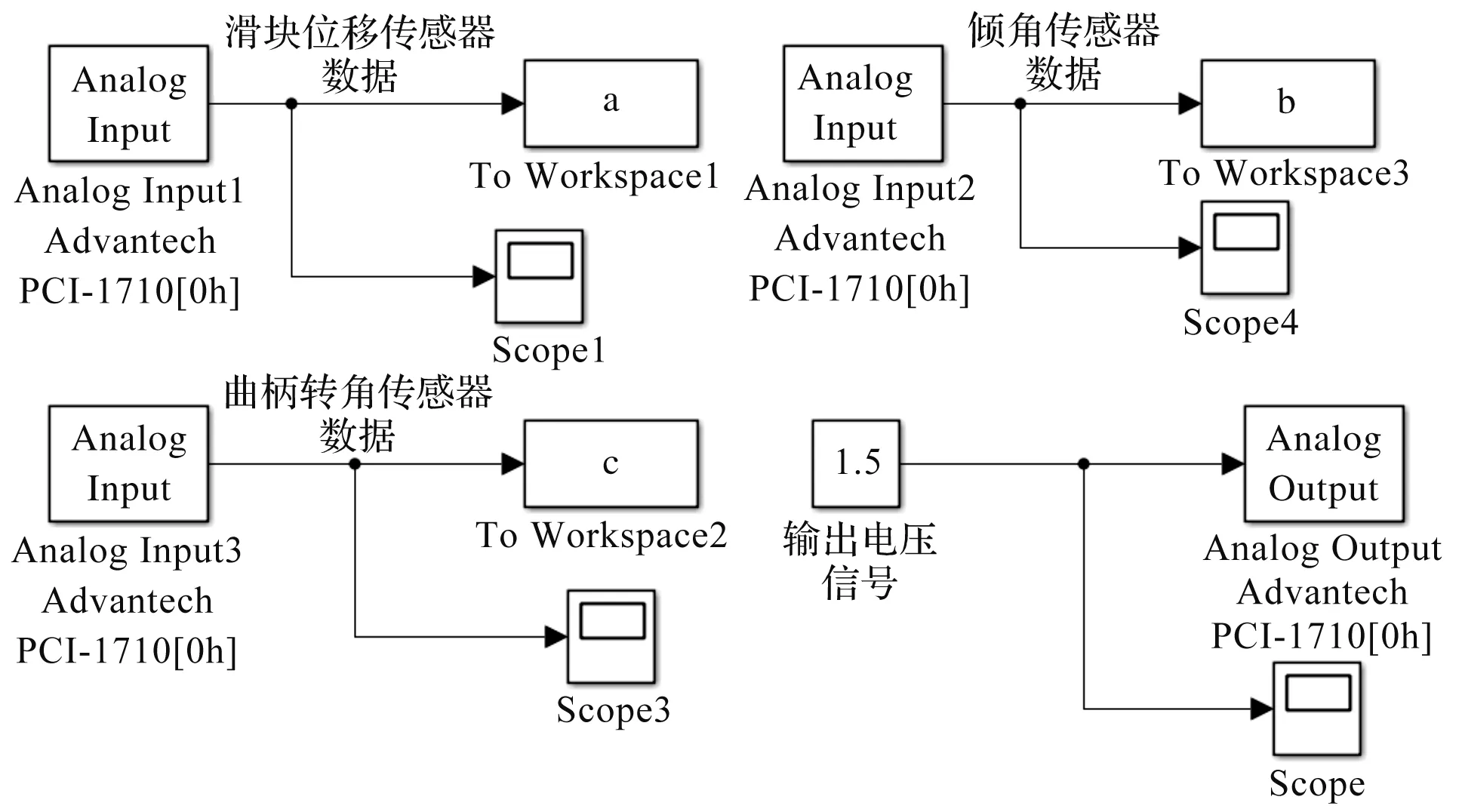
图5 实验数据采集RTW平台

图5中,曲柄转角、连杆倾角和滑块位移的传感器输出数据由3个Analog Input模块采集测量,Analog Output是信号输出模块;采集之前需将每个数据点的采样频率设置为0.005 s。

2.3 仿真模型验证

RTW平台获得的实验数据是电压,滑块位移需要对实验数据进行处理才能得到,其式为:

(21)

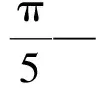
用MATALAB将处理后的实验数据和仿真模型的数据对比,便可得到考虑间隙的曲柄滑块机构模型滑块位移和实测滑块位移的比较图。

考虑到实验的客观性,此处分别选取电机转速在1 200 r/min、1 500 r/min和1 800 r/min时,对滑块的位移和误差进行测量,其结果如图6所示。

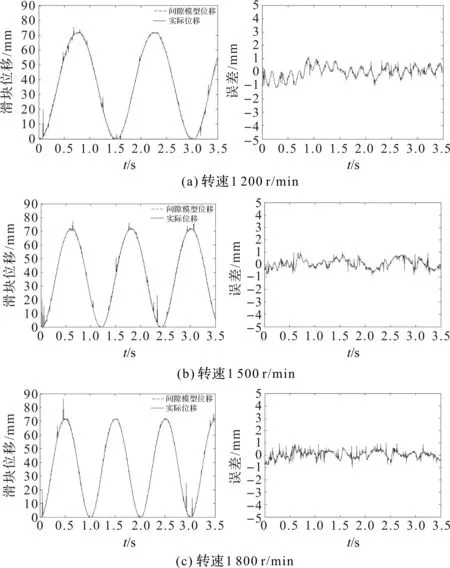
图6 滑块位移(左)和误差(右)

从图6中可以得出:采用不同的运行转速,含间隙模型与实际系统的输出吻合度较高。

为衡量不同转速下两组数据之间的波动程度,笔者计算两组数据的均方差,即:

(22)

式中:Ri—滑块位移实测值;ri—滑块位移仿真值;n—数据个数。

均方差计算的结果如表4所示。

表4 滑块位移误差的均方差

由表3可以看出,滑块位移误差随着电机的转速增加而减小。产生这种情况的原因是:当曲柄滑块机构滑块运动到极限位置时,方向发生改变;速度越快,轴销反向通过轴销和轴套之间间隙的时间越短,而误差越小。

3 误差补偿

理想的曲柄滑块模型和实测数据的对比如图7所示。以下仅给出电机转速在1 200 r/min时的对比。

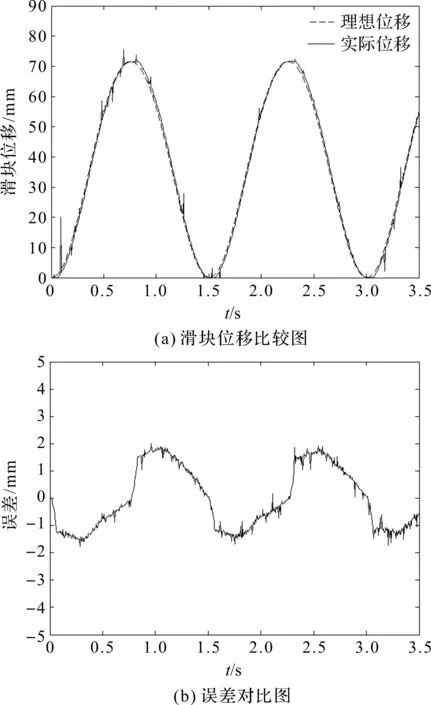
图7 滑块位移和误差对比

由图7可知:两者之间有较大误差,误差峰值达到了1.943 mm,此处的均方差经计算为1.151 mm。原因是曲柄滑块机构除了文中提到的连杆和滑块铰连接处含间隙,在机架和曲柄、曲柄和连杆这两个连接处同样存在不同程度的间隙;本文中的含间隙模型仅考虑了其中较大的连杆和滑块之间的间隙。当滑块运动到极限位置时,轴销反向运动通过间隙需一定时间,导致实际系统运动情况较理想机构有所滞后,需对实际系统进行误差补偿。

3.1 含间隙曲柄滑块机构的逆模型

系统∑具有u(t)=(u1,u2,…un)T这样的n维输入和y(t)=(y1,y2,…ym)T的m维输出,初始状态x(t0)=x0,输入、输出间关系可用式(23)表示:

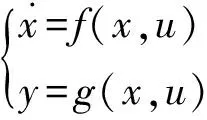
(23)

从式(23)可以看出:系统的数学模型等价于一个从n维输入到m维输出的映射,该映射输出完全由初始状态x(t0)=x0和输入u(t)确定。

用函数θ描述这一映射关系,即:

y(·)=θ(x0,u(·))

(24)

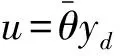
其中,输入yd(t)=(yd1,yd2,…ydm)T是可微函数向量,输出向量记为:u(t)=(u1,u2,…un)T。

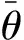
(25)

则称模型∏为系统∑的单位逆模型,∑为原系统模型。结构如图8所示。

图8 单位逆模型与原模型复合结构

图8中,将∑的期望输出yd(t)作为∏的输入,而逆模型∏的输出恰是∑的输入控制量u(t)。根据这一思想建立含间隙曲柄滑块机构逆模型时,闭环矢量方程式(6)不变,将式(7,8)两边同时平方可得:

(26)

(27)

将以上两式相加化简得:

(28)

因为在建立逆模型时,换r1为输入,ω2为输出,所以式(28)可改写为:

(29)

将其作反余弦函数得:

(30)

构建后的逆模型如图9所示。

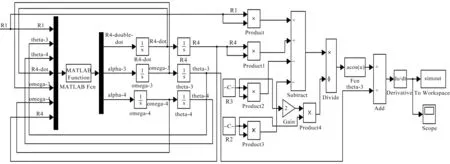
图9 含间隙曲柄滑块机构逆模型

图9中,逆模型由r1作为输入,ω2作为输出,将式(6～20)组装成矩阵,嵌入MATLAB中的function模块,求解出θ3和r4,然后输入到式(30),再求解出ω2。

3.2 逆模控制

本文根据图8构造一个含间隙曲柄滑块机构的逆模型,作为补偿器的逆模控制进行误差补偿,如图10所示。

图10 逆模控制

补偿效果如图11所示。

分析比较图11(a,b)可以得出:在系统中加入逆模控制后仍然有误差,计算得误差均方差为0.852 3 mm,使系统稳定性提升25.9%;为得到更明显的效果,笔者在此基础上加入了PID控制。

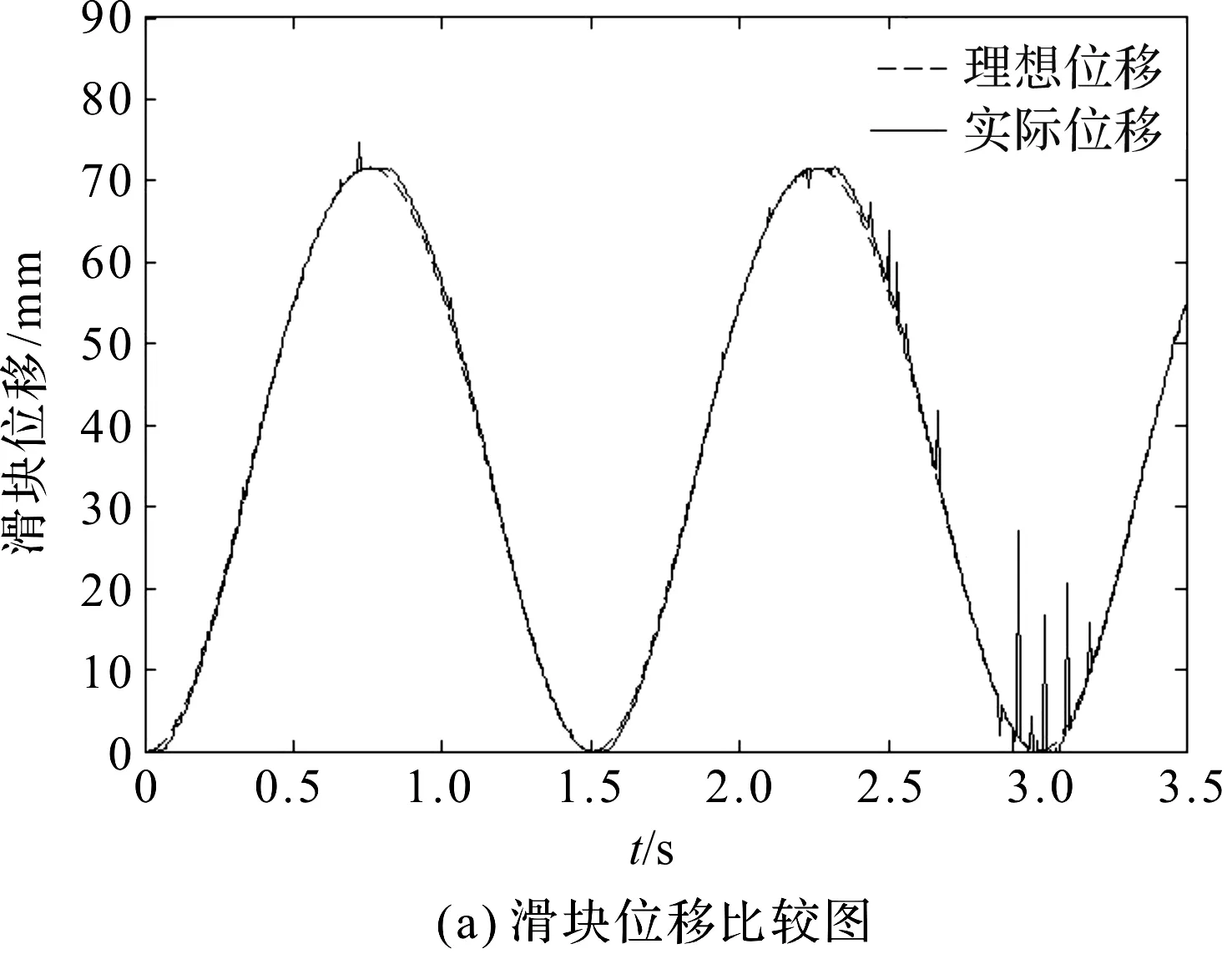
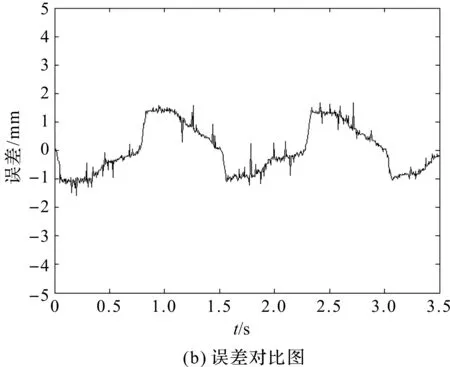
图11 逆模补偿后的输入输出

3.3 PID加逆模控制

为获得更好的补偿结果,笔者将建立的逆模型和PID控制相结合进行误差补偿,如图12所示。

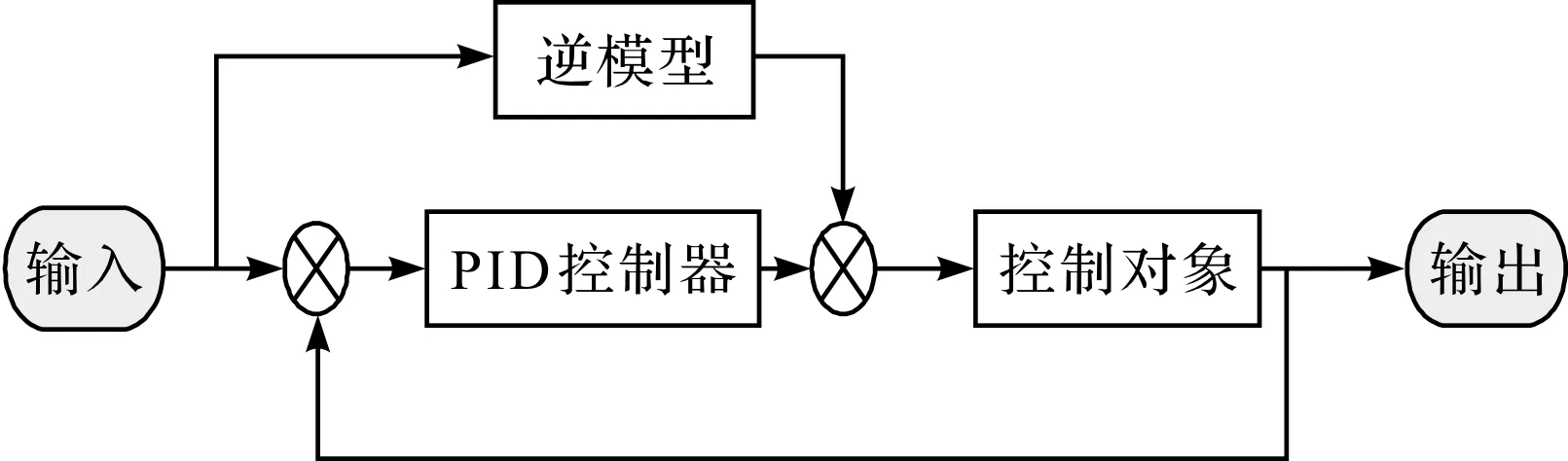
图12 PID加逆模控制

仿真平台如图13所示。

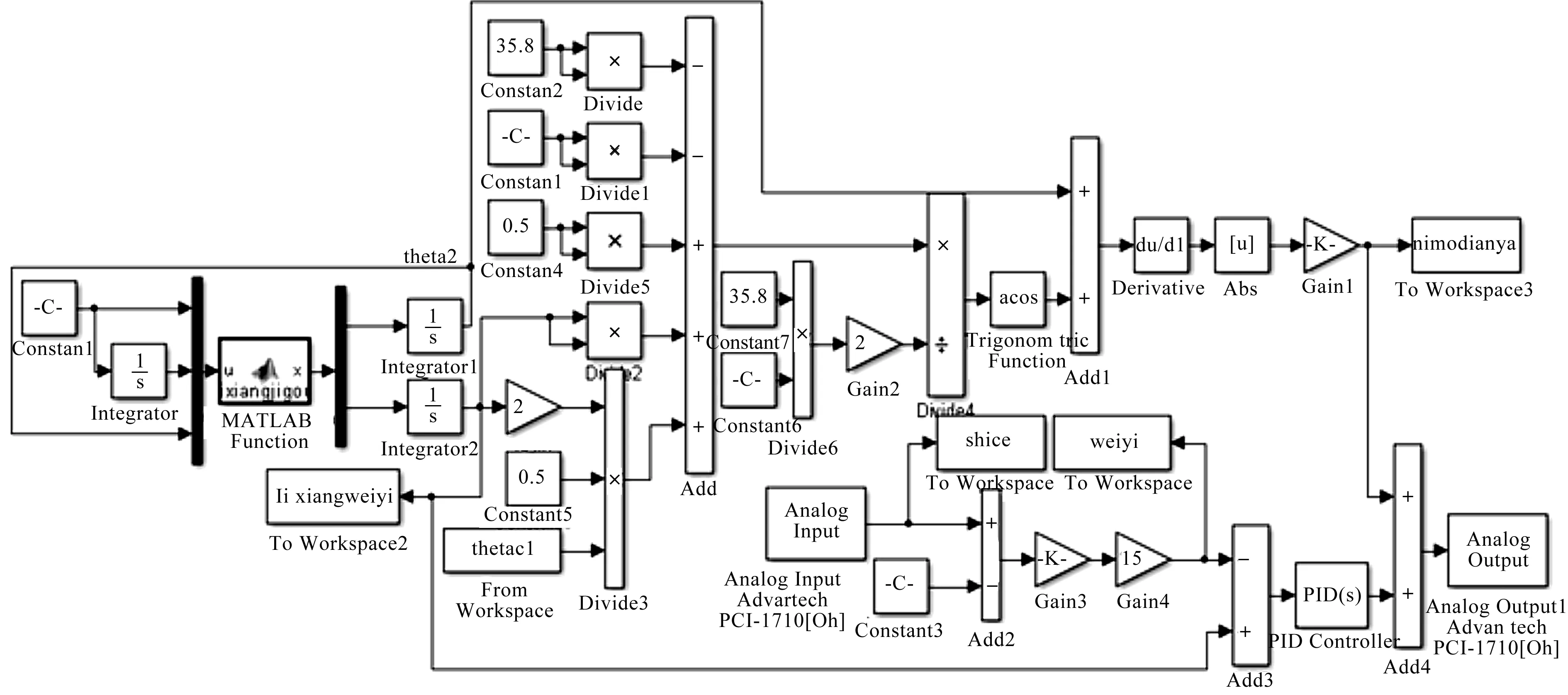
图13 PID加逆模控制仿真平台

在该补偿方法中,PID和逆模控制器的双重作用保证了系统输出信号对输入信号的跟踪精度。

PID加逆模补偿后滑块位移误差的均方差如表5所示。

表5 PID加逆模补偿后滑块位移误差的均方差

补偿效果图如图14所示。

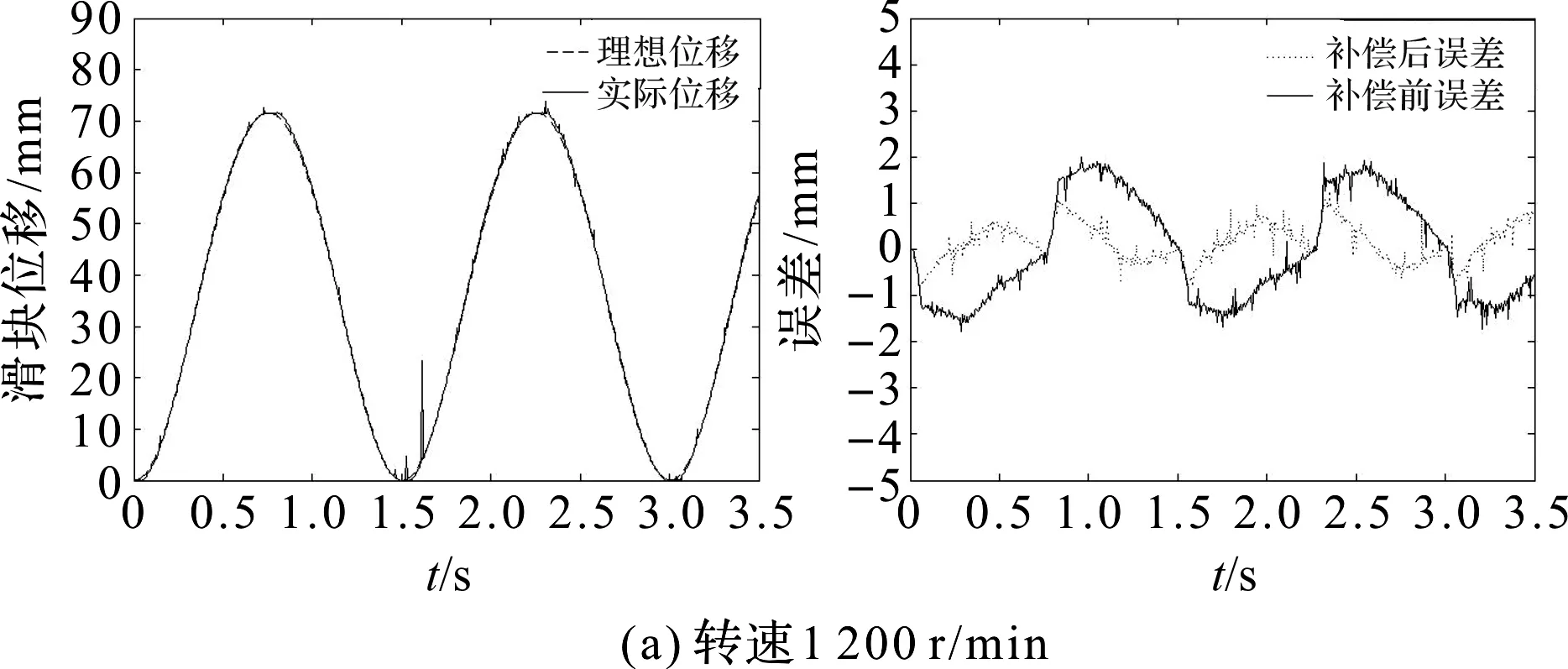
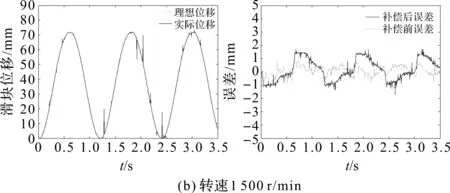
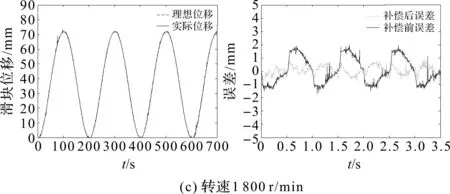
图14 补偿效果图{滑块位移(左)和误差(右)}

从图14和表5可以看出:PID的引入使得误差和均方差均变小,信号跟踪精度又一次得到了提高。

4 结束语

笔者针对含间隙的强非线性系统难以建立较准确数学模型的问题,运用Nikravesh非线性弹簧阻尼碰撞模型,对含间隙曲柄滑块机构进行了动力学建模,并对其建立了逆模型,就其带来的误差分别应用逆模控制和PID加逆模控制进行了补偿。理论研究和实验结果表明:

(1)采用非线性弹簧模型所建立的含间隙曲柄滑块机构模型仿真结果和实验测量结果之间的误差处于合理范围之内;

(2)该逆模型误差补偿策略有较好的补偿效果,具有较强的工程应用价值,可以作为误差补偿的有效途径,为复杂的非线性系统误差补偿提供新的方法和途径。

在下一步的研究中,笔者将考虑到含间隙机构建模的过程中可能存在的各种间隙进行建模,使模型更符合实际情况,且大幅提高模型运算速度。