基于振荡气泡法测定声悬浮液滴的表面张力

蒋乐昕，郭泽虹,黄敏珊，彭 力,b,c

(华南师范大学 a.物理与电信工程学院；b.华南师大(清远)科技创新研究院有限公司;c.物理国家级实验教学示范中心，广东 广州 510006)

超声悬浮是利用超声波的非线性效应产生声辐射力，从而克服悬浮物的自身重力，实现物体悬浮的技术，广泛应用于液体样品的无容器操纵，对液滴动力学研究有重要意义.

表面张力测量可为人们提供气液、液液之间相互作用的信息，通过这些信息可以推断出材料的黏附、浸润、生物相容、润滑、吸附等重要特性[1]. 传统测量液体表面张力的方法有拉脱法、悬滴法、最大气泡法和毛细管上升法等. 目前最常用的方法是拉脱法，该方法所使用的仪器简单[2]，但操作过程复杂，易受环境干扰，样品与固体表面直接接触，易污染样品，且由于人为操作的影响导致实验误差大. 利用声悬浮技术测量液体表面张力是近年发展起来的新方法. Tian等人[3]将拍摄的悬浮液滴图像进行轮廓提取，利用悬浮液滴平衡形态，以液滴的表面张力为待定参量，发展出计算液滴表面张力的理论方法，然而该方法仅在平衡态悬浮液滴近球形时适用. Shen等人[4]修正Rayleigh公式,对声悬浮液滴的振荡频率进行描述，从而测得液体的表面张力，实验结果与文献基本一致，证实了该方法的可行性. 但该方法对使用的仪器要求较高，需采用高速CCD进行图像拍摄和图像处理才能判断液滴的振荡阶数，且不同大小的液滴，每一模态的调制频率不同，需进行大量的调试.

本文通过研究声悬浮液滴的特性，制作了悬浮气泡，对振荡气泡法理论公式进行修正，再与数字图像轮廓提取方法相结合，即可测量悬浮液体动态表面张力，实现了悬浮液滴拍摄、图像处理、表面张力计算一体化的非接触测量.

1 声悬浮原理

声悬浮是在高声强条件下的一种非线性效应，其基本原理是利用声驻波与物体的相互作用产生竖直方向的悬浮力和水平方向的定位力，分别克服物体重力和将物体固定于声压波节处的力.

假设2个发射端的距离为L，通过调节L，可以实现声悬浮所需要的驻波条件，将声场近似看作平面驻波，则驻波的条件为

(1)

2个发射面是声压的2个波腹，声压波节位于λ/4，3λ/4，5λ/4，…，由于声辐射力具有回复力的特性，当样品偏离波节时，就会被拉回原位置，所以声压波节就是样品的稳定悬浮位置. 故悬浮样品个数最多为n，且2个样品之间的距离为λ/2.

假定声源的振动方程按余弦规律变化，则声场空间中声波的波动方程可写为

y1=Acos (ωt-kz).

(2)

式中A为振幅，ω为角频率，k为波矢，z为沿波传播方向任一体元的平衡位置的坐标. 根据理想流体媒质的运动方程，声场中声压p为

p=-2Aωsin (ωt)cos (kz).

(3)

根据Gor’kov关于声悬浮的理论[5]，作用于半径为R的小球上声辐射时间平均势U为

(4)

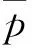
F=-U.

(5)

因此，要使物体能够稳定悬浮，需声波谐振腔的长度恰好是该声波的整数倍. 此外，本文结合不同悬浮装置的优缺点，采用单轴式凹球面相控阵列悬浮系统进行实验，满足在液滴动态非平衡状态下测量液体表面张力. 实验中通过调节声场频率，利用悬浮液滴制作气泡，为液体表面张力的测量提供便利.

2 气泡制作原理

实验过程中通过调节声场或声强的分布，在液体表面张力作用下悬浮液滴的形状发生改变. 液滴收缩使得液滴表面积减小，当悬浮液滴的体积达到某一临界值时，液滴的振动频率与声场频率相同，液滴与声场发生共振，导致液滴突然膨胀，从而形成封闭的气泡[6].

液滴悬浮于声场时,液滴的平衡形状由声辐射压力pA、表面张力和液滴内部压力决定[7]：

pi-pA=σn.

(6)

式(6)中pi为液滴内部压强，pA为液滴外部压强，σ为液体表面张力。为更直接地描述液滴平衡形状,在极坐标下,液滴的形状函数可写为

(7)

其中θ为液滴轮廓的极坐标，RE为液滴赤道半径，ρ为液滴的密度. 液滴表面声辐射压分布不均匀,使得悬浮于声场中的液滴不再是球形. 声场强度(声压)是决定声悬浮液滴形状的主要因素,重力只改变液滴的悬浮位置,对其形状几乎没有影响，图1为不同声压条件下声悬浮液滴的平衡形状.

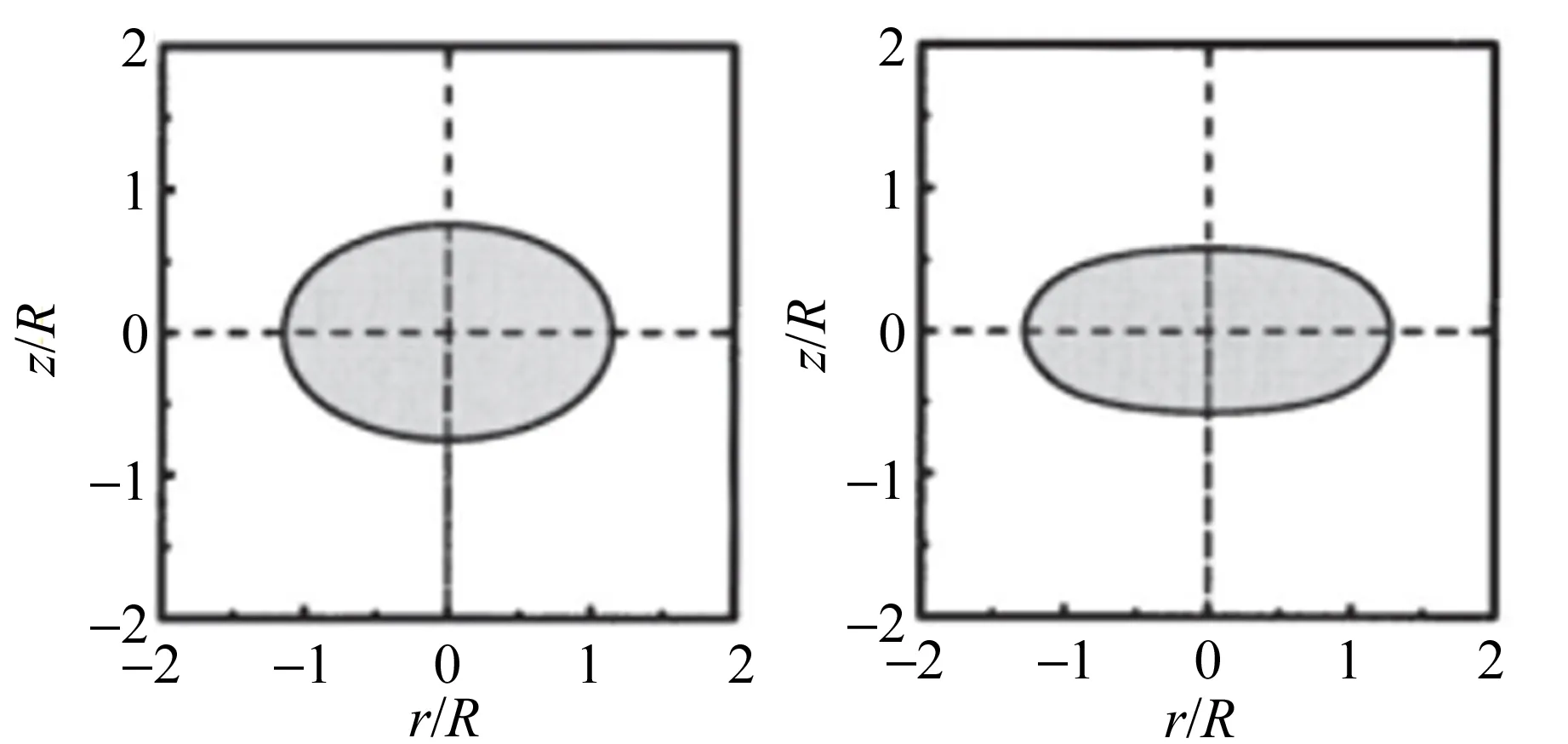
(a)0 g,161 dB (b)0 g,163 dB

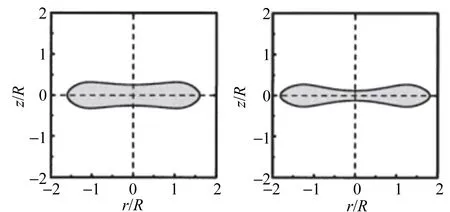
(c)0 g,165 dB (d)0 g,166 dB

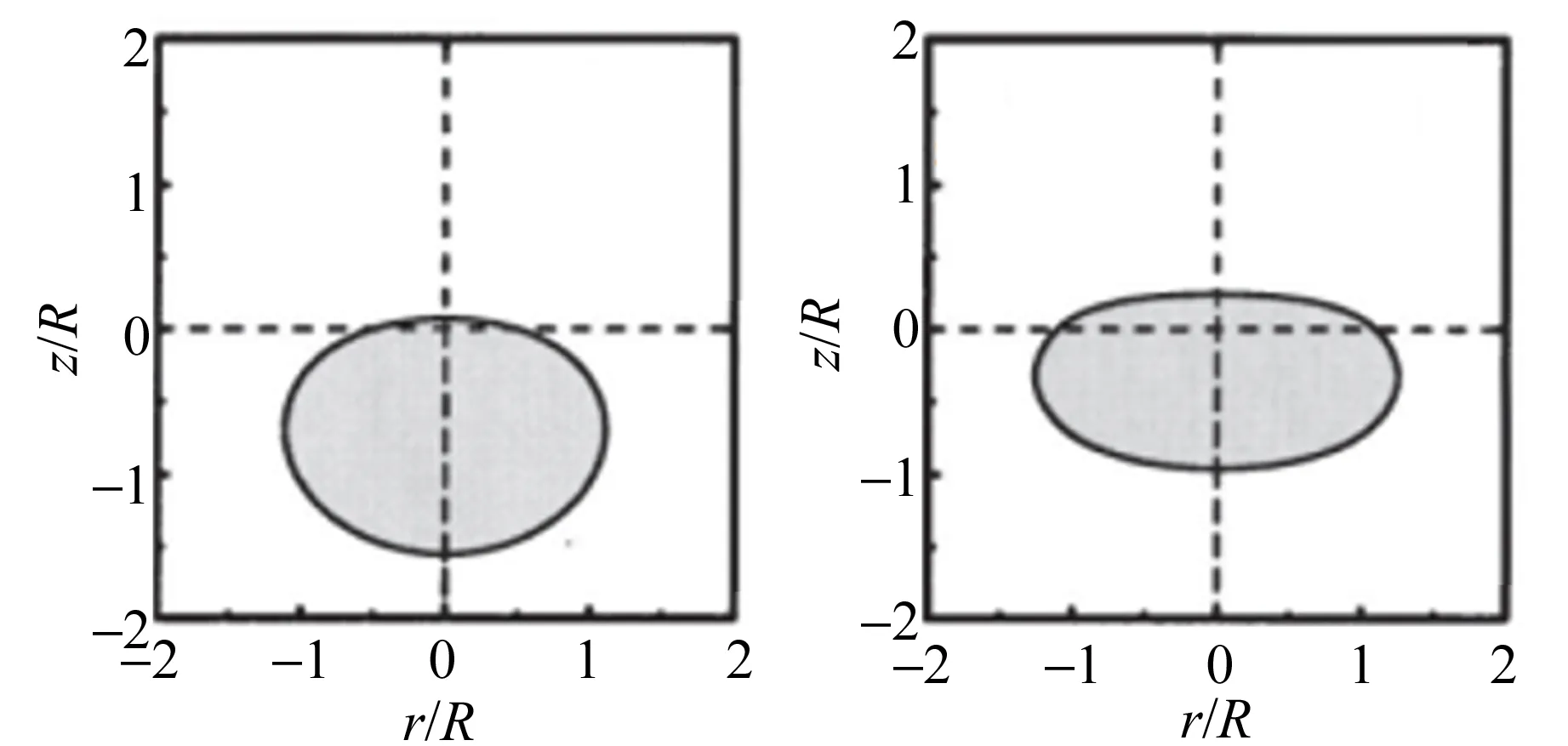
(e)1 g,161 dB (f)1 g,163 dB

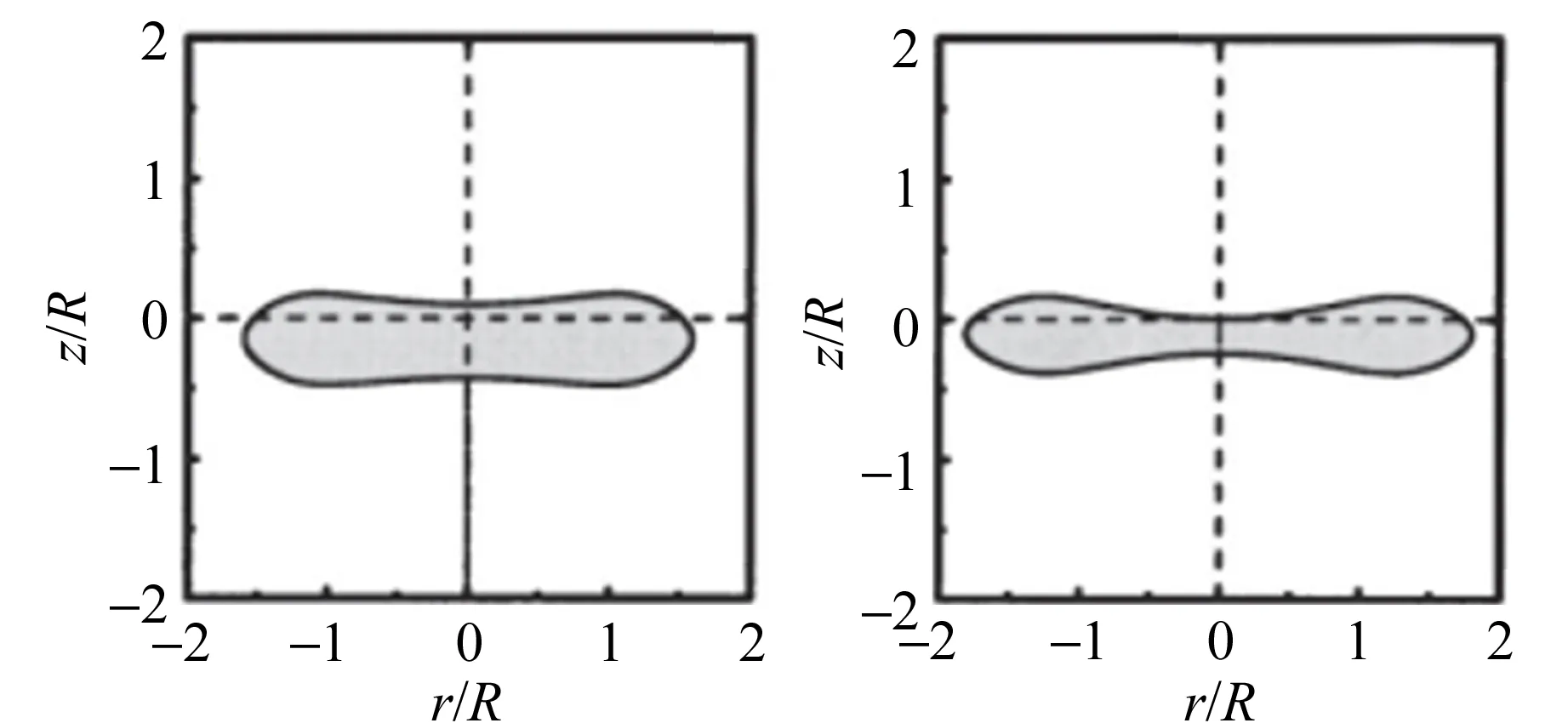
(g)1 g,165 dB (h)1 g,166 dB图1 不同声压条件下声悬浮液滴的平衡形状

根据理论研究，液滴受到的声辐射压力为

(8)

其中,p是声压，c0是声速，ρ0是空气的密度，V是介质粒子速度. 当液滴形状接近扁平时[如图1(b)]，其下表面声辐射压力大于上表面声辐射压力，可知液滴被超声波向上推动，以平衡重力的影响；当液滴形状为凹状时[如图1(c)]，上表面的声辐射压力更大. 从图2中可以看出随着声压的增加，液滴的弯曲程度增加.

为了更好理解液滴到气泡转变的动力学过程，本文分析了液滴/气泡薄膜的表面积随时间的变化过程. 随着声压增加，食用油液滴的表面积变化可分为6个不同的阶段，如图2所示.

从阶段(d)到阶段(e)，液膜的表面积急剧增加，表明液滴-气泡发生转变. 液滴表面积随着声压的增加而不断增加，而对于任意给定的声压，液滴都将在表面张力的作用下呈现其稳定的形状.

综上所述，由于声压以及液体表面张力的作用，使得液体的形状发生改变，并呈现液滴表面积缩小的趋势；当液滴中间空气腔通过弯曲达到适当的体积时，液滴会与相控阵列悬浮装置发出的声场产生共振，能够显著增强能量吸收，在这种情况下，空腔内的空气分子强烈振动，使得腔内声压高于空腔薄膜外部声压，从而导致空腔体积突然膨胀，形成气泡. 因此，利用声悬浮装置可制作气泡.

(a)轻微变形 (b)快速变平

(c)缓慢变平 (d)翘曲

(e)突然膨胀 (f)边缘闭合图2 液滴到气泡的转变过程

实验中，液滴通过共振机制形成气泡. 因此，声能可在ms时间内被有效吸收，并转变为气泡表面能. 在这种情况下，声波不仅提供了抵抗重力的悬浮力，还提供了产生新表面能的能量.

3 表面张力测量

3.1 振荡气泡法

目前普遍利用落点张力计测量液滴表面张力，根据液滴或气泡的形状，再通过高斯-拉普拉斯方程求解表面张力. 但高斯-拉普拉斯方程是针对静态条件推导而来的[8]，在声悬浮场中，流体动力效应导致液滴和气泡轮廓偏离拉普拉斯形状. 因此需寻求其他方法测量声悬浮的液滴或气泡表面张力. 本文采用的振荡气泡法适用于超声悬浮场中小的球形气泡表面张力的测量[9].

已有实验证明非平衡状态下表面分子的膨胀系数能够解释表面张力[10]. 根据Maru等人[11-12]的建议，新建模型用成分效应和内在效应来表征液滴或气泡膨胀特性. 成分效应描述表面组成与表面张力的关系，而表面层内弛豫过程对表面张力的影响由内在效应描述. 二者对表面张力的影响由非平衡状态下的表面膨胀系数来表征.

3.2 非平衡动态表面张力模型

用Boussinesq-scriven方法定义后续测量气泡表面张力的流体动力学参量，气泡二维黏性表面的应力[13]为

(9)

其中，i,j=1,2；γ表示动态表面张力成分效应；η表示表面剪切黏度，κ表示表面膨胀黏度，二者表征弛豫行为；vi表示表面速度分量，x1和x2表示面坐标. 将三维流体压力张量形式变换成二维形式可简化表面张力的计算，但由惯性导致的压力张量发散会影响到式(9)的适用性，因此需要对其进行修正. 在本文中，认为在声悬浮非平衡状态下气泡是1个或几个分子组成的厚度为L的表层，以抵消压力张量的发散，从而减小表面张力计算的误差[12].

由于气泡表层可进行快速的分子交换，具有可变成分的高度可压缩流体相，但根据纳维尔-斯托克斯方程[11-12]的边界条件，只有在解释部分波动实验[14-15]获得的负表面黏度值时，才需考虑这种分子交换，因此本文假设分子交换过程对声悬浮液体表面流变性质没有影响，不产生附加项. 故声悬浮气泡可视为均匀膨胀或压缩，使得二维应力张量方程的剪切分量为零，得到应力张量的纵向分量为

(10)

这是单层或定义厚度较小的气泡层引起扩散效应的数学表达式，最后一项满足描述气泡表面微小正弦膨胀现象的流体动力学效应条件，该条件为

(11)

其中,vs是表面速度矢量，s是表面速度梯度算符. 一般情况下，由该条件推导得到的表面膨胀系数为

(12)

膨胀系数ε(f，ci)是频率f和表面层平衡体积浓度ci的函数[16-18]，仅适用于平衡状态流体，对于缓慢变形(f<1 Hz)非平衡态的声悬浮气泡，利用式(12)无法描述气泡表面张力变化，需修正得到适用于非平衡状态流体的表达式，再利用实验测得相关参量，再通过修正后的表达式计算出气泡的表面膨胀系数.

气泡进入非平衡状态是因为声场相位信号改变使表面层分子交换运动被延迟，用函数h(f,c)来描述该状态[19]：

|h(f,c)|exp [(-iβ(f,c)].

(13)

函数h(f,c)表示在扩展表层内浓度cs的变化与虚拟扩展表层内浓度c*的变化情况，其中D表示气泡的表面扩散率，k为分子交换动力学常量. 用式(13)描述非平衡状态表层分子交换过程对表面膨胀模量的影响，而对于声悬浮液滴或气泡这类非平衡态，分子交换函数实际表达式ζ必须用复表达式代替式(13)才准确：

ζ′=h(f,c)ζ.

(14)

将式(14)和所涉及的流体动力学效应条件代入式(13)可得传统表面膨胀模量ε[20]为

(15)

式中εm为内最大膨胀系数. 然而，式(15)不能在整个声悬浮频率范围内准确计算动态表面张力，需进一步修正. 声悬浮频率在f→0时，分子交换极快，气泡相位极限趋于β=45°. 利用相位修正非平衡动态表面膨胀模量，得到其满足的方程为：

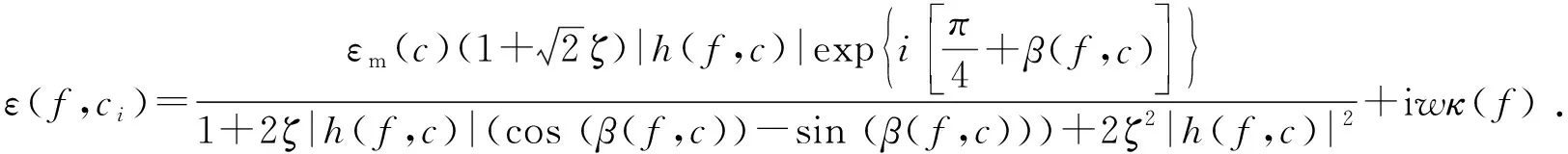
(16)

利用装置拍摄气泡，经过预处理测量其赤道半径和振荡频率f.计算该气泡的表面积A及对应的最大膨胀模量εm、角频率ω和相角β(与频率f和c有关)，再将气泡的表面扩散率D、动力学常量k代入式(16)，计算得到对应的气泡表面膨胀模量ε.测量气泡的表面膨胀模量后，即了解声悬浮气泡的表面张力变化，因表面膨胀模量ε定义为表面张力γ在恒定温度下相对于气泡表面积的小幅增加，即:

(17)

由(17)式即可计算得出液体动态表面张力γ，达到实验预期目标.

4 实验装置及数据处理

图3所示实验装置由悬浮部分、驱动板、控制模块、图像采集系统、分析系统、暗箱及照明系统组成. 悬浮部分为凹球面超声阵列结构，该结构由72个超声换能器和支撑架组成，如图4所示. 支撑架上下2个凹球面分别固定32个压电式超声换能器. 驱动板采用L298N模块用于驱动超声波传感器，控制模块使用FPGA开发板. 根据需求设计算法架构，实现对声场的调节从而改变声场信号的相位，控制表面膨胀黏度κ，同时规律调节频率可完成气泡制作并改变气泡的最大膨胀模量εm.

暗箱可屏蔽空间中除声场外大部分气体的流动干扰，将声悬浮装置垂直置于长方体暗箱内部左侧，固定光源和摄像头后进行实验. 实验样品为锅炉用油[17]，浓度为4.2×10-11mol/cm3. 连通电源并预热设计的实验装置，利用针管提取一定量的液体并挤压液体进入声场，调节凹面相控阵列的工作信号，实现液滴稳定悬浮.

采用Matlab软件对摄像头捕捉的液滴振荡形态图进行分析，获取液滴振荡模态及频率信息，并通过边缘检测，提取液滴轮廓. 实验步骤如下：

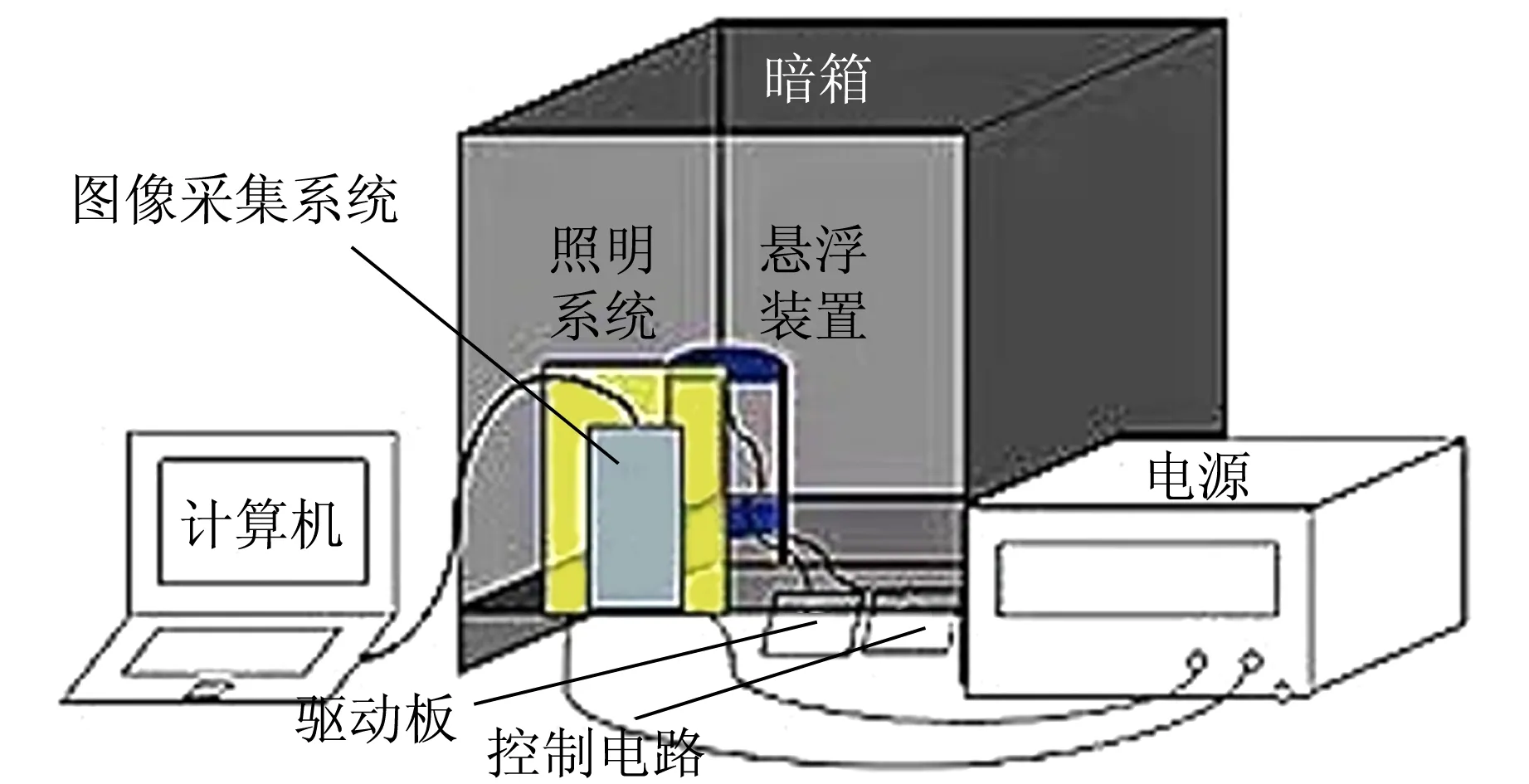
图3 实验装置示意图

1)连通电源并预热实验装置，利用针管提取一定量的油滴.

2)利用针管挤压油滴进入声场，调节FPGA的输出功率来实现对悬浮液滴的径向操控，直至悬浮液滴抵达合适的位置.

3)在保持液滴径向位置不变时，通过控制换能器的电压激发悬浮液滴产生非轴对称大幅振荡.

4)使用高清摄像机进行拍摄，捕捉液滴高速变化的振荡图像，导入Matlab软件进行数字图像处理和分析. 电压与时间的关系需要满足：

V=V0[1+ηcos (wmt)]cos (wact),

(18)

式中,V0为不加调制时换能器的输入电压，η为相对调制幅度，wm为调制频率，wac为超声频率. 为了保证液滴在该实验条件下始终处于稳定悬浮的状态[5],选取在较高的悬浮声压和较小的调制幅度下进行实验.

5)去除干扰信号，保留边缘灰度信息，采用Canny法识别液滴的边缘点，提取液滴轮廓.

6)根据非平衡状态下气泡对应的动态表面张力与弹性模量所满足的关系式,编写液滴表面张力测量程序.

7)输入液滴边缘轮廓信息，利用计算机进行数字图像处理，处理过程如图5所示.

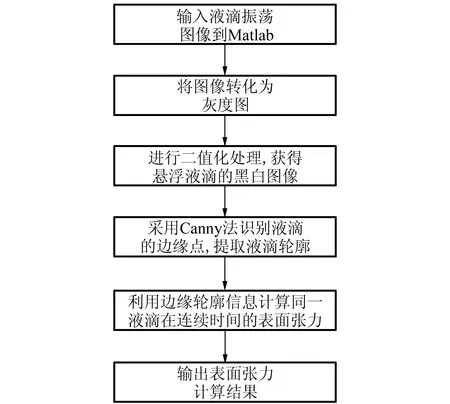
图5 数字图像处理过程

综上，只需将待测液体在声场中悬浮，用摄像机拍摄振荡图像传入编写的Matlab程序，即可计算出表面张力.

5 结果与讨论

采用如图3所示的实验装置进行多次实验，使用基于原理编写的程序，自动计算同一气泡在连续时间的表面膨胀模量及对应的表面张力，图6为Matlab实时处理的二值化气泡轮廓图. 观察到气泡随声压调节过程中可在一定范围内膨胀和压缩后，进行动态表面张力测量. 为避免实验过程中液体蒸发导致浓度变化产生较大的实验误差，实验应尽可能迅速完成. 气泡表面压缩开始时，经不均匀的时间间隔拍摄图片，并取其中在30 s内完成随声压增大/减小而压缩/膨胀的气泡完整图像，导入计算机端进行分析，得到对应实验数据，并多次重复实验以减小误差. 通过数字图像处理方法提取气泡轮廓，计算液体表面膨胀模量来确定气泡的表面张力. 结果如表1所示.

(a) t=0 s (b) t=1 s

(c) t=1.6 s (d) t=1.8 s

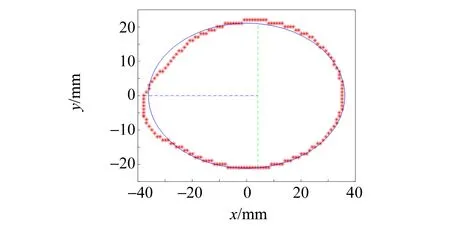
(a) t=0 s

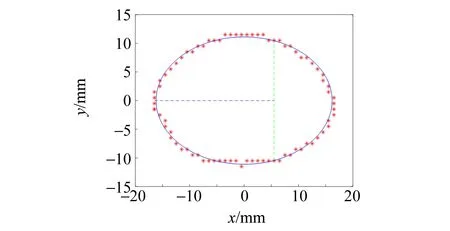
(b) t=1 s

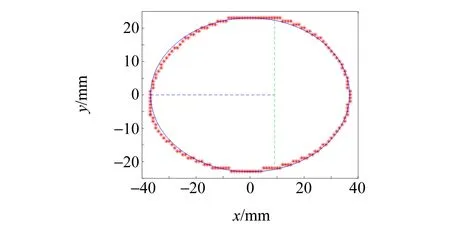
(c) t=1.6 s

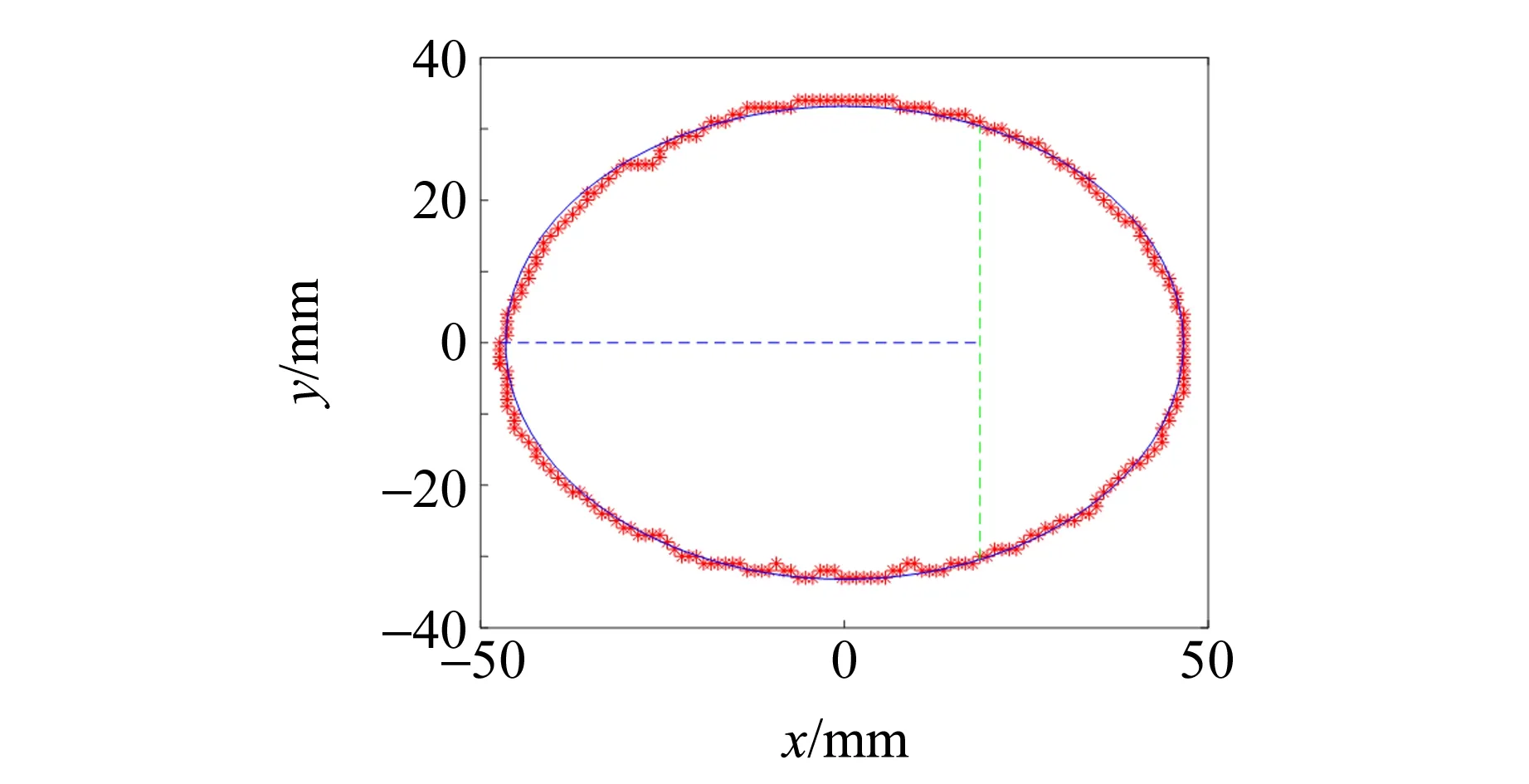
(d) t=1.8 s

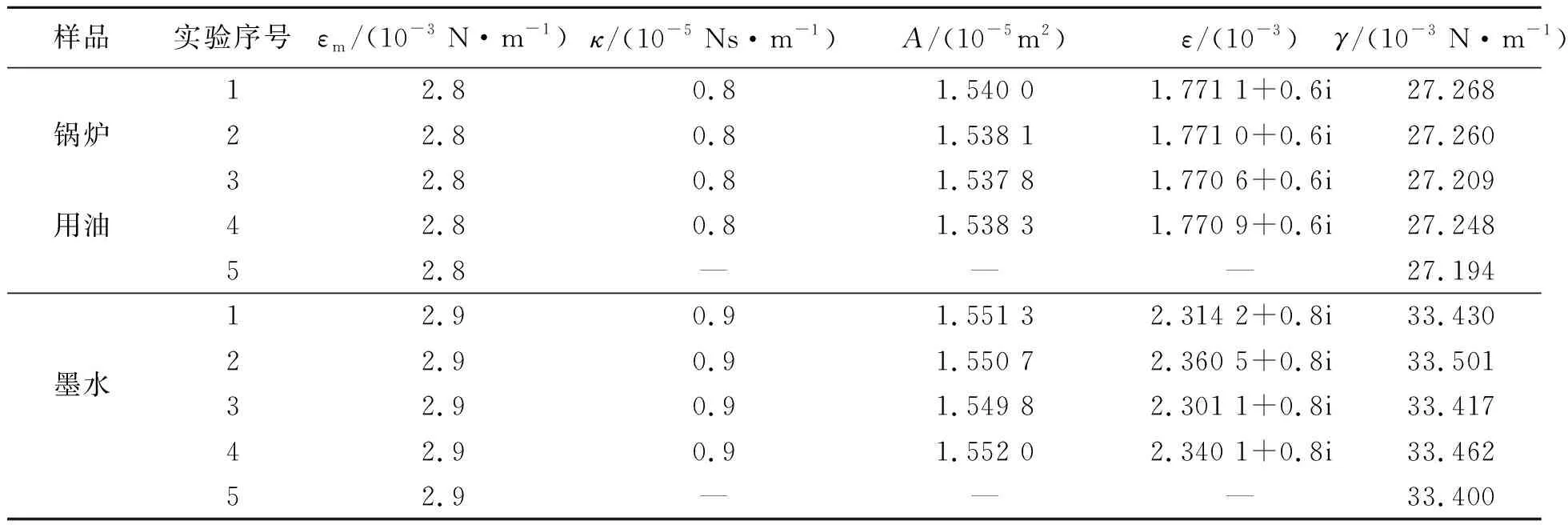
表1 样品表面张力测量结果

6 结束语

本文对声悬浮液滴和气泡现象进行了分析，设计装置实现液滴和气泡的悬浮，在此基础上测量了液体的动态表面张力. 本文所用方法具有操作简单、测量效果良好的特点. 在接下来的工作中，可以建立数学模型对实验数据进行定量的分析，讨论相控阵列功率、液滴颜色、气泡厚度等对表面张力的影响，从而了解非平衡状态下声悬浮液滴动态表面张力的测量机理.