用等浓度薄层移动法测量液相扩散系数
王瑞仙,钱春霖,王 艳,孟伟东,普小云
(云南大学 物理与天文学院,云南 昆明 650091)
液相扩散系数是研究传质过程,计算传质速率及化工设计与开发的重要基础数据,广泛应用于物理、化工、生物及医学等领域中[1-4]. 膜池法、泰勒分散法和全息干涉法是测量液相扩散系数的3种传统方法. 其中,膜池法所需操作时间长,而且需要对实验系统进行膜池标定[5];泰勒分散法由于设备加工精度的限制导致其测量精度较低[6];全息干涉法测量精度高, 但对实验装置的稳定性要求高, 测量时间较长[7].
为解决上述存在的问题,李强等[8]基于玻璃毛细管对芯区溶液折射率的空间分辨测量能力,提出了用玻璃毛细管测量液相扩散系数的方法——等折射率薄层移动测量法. 该方法较好地解决了传统测量方法存在的测量速度慢、抗环境干扰能力弱等问题,并具有样品需要量少、测量速度快、系统稳定性好等特点[9-10]. 但在确定等折射率薄层位置时,推导并计算出液芯柱透镜的焦距与芯区液体折射率的关系f(n);在确定等折射率薄层对应的溶液浓度时,用实验方法测量并拟合出溶液的浓度与折射率[11]的对应关系C(n). 为简化测量过程,进一步缩短测量时间和提高测量精度,本文基于消球差液芯柱透镜搭建了光学测量体系,提出用等浓度薄层替代等折射率薄层的方法测量液相扩散系数. 无需计算f(n)和测量C(n) 关系,用等浓度薄层移动测量法即可测量液相的扩散系数. 本文采用该方法在室温下(25.0 ℃)测量了葡萄糖水溶液的液相扩散系数,结果表明:此测量方法具有装置和操作简单、结果可靠、扩散过程可视化等特点,是利用基础光学知识和基本光学元器件测量液相扩散系数的有效方法.
1 实验原理
1.1 成像原理
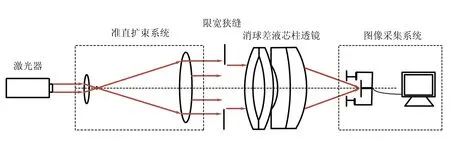
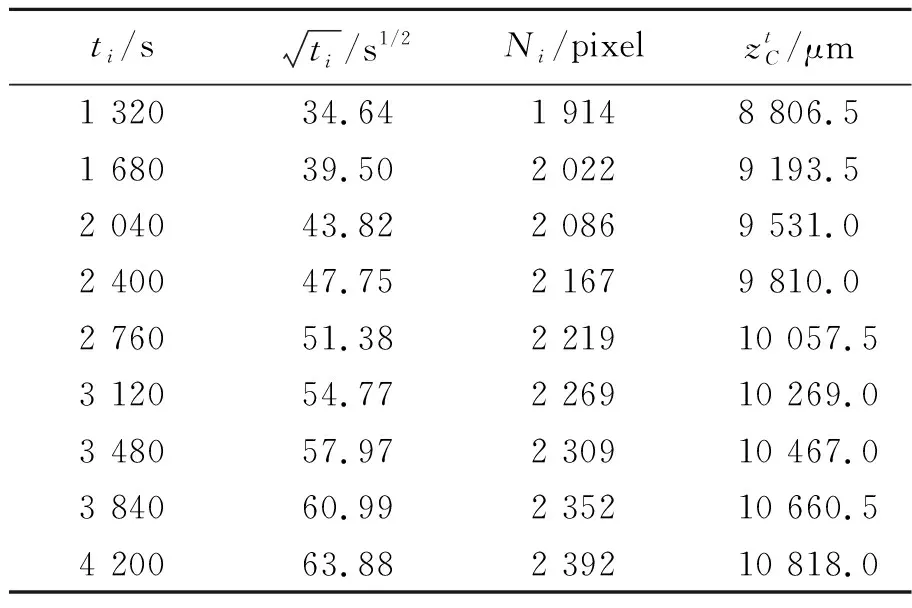
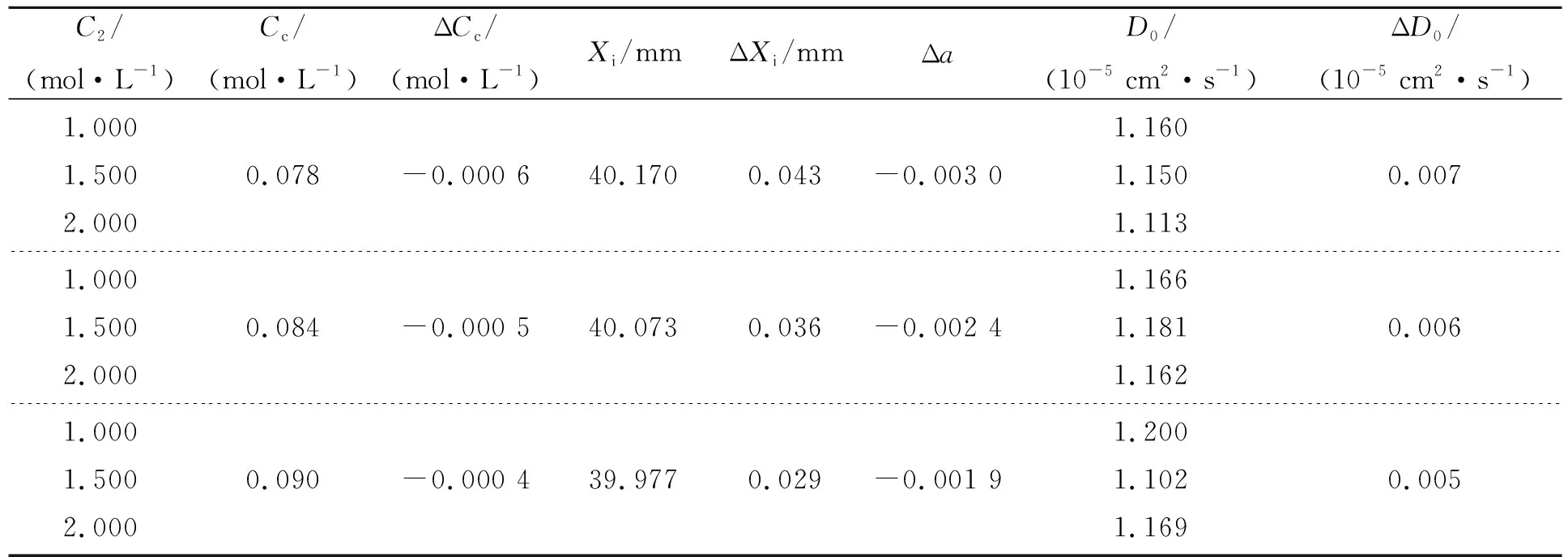
消球差液芯柱透镜由2片对称液芯柱透镜和2片胶合在一起的辅助透镜构成[12],如图1所示. 对称液芯柱透镜的芯区具有扩散池作用,辅助透镜具有消球差作用. 在液芯柱透镜内注入浓度为C1的液体,单色准直光束经过液芯柱透镜后,在其焦平面上会聚成1条明亮的细线,如图1(a)所示. 在液芯柱透镜内上、下半区分别注入浓度为C1和C2的液体(C1 (a) (b) (c)图1 消球差液芯柱透镜成像原理图 由于扩散是动态过程,扩散图像随时间的变化能够可视化地表现出微观分子的扩散运动;扩散图像束腰位置的移动速率,可用于测量扩散体系的液相扩散系数. 在非稳态扩散过程中,扩散溶液的浓度分布C(z,t)是时间的函数,该函数满足Fick第二定律,用二阶偏微分方程可以表示为 (1) 其中,D表示扩散系数,一般而言,D是浓度的函数,即D=D(C),因此式(1)可以展开为 (2) 式(1)和式(2)没有解析解. 但对于小浓度差[∂C(z,t)/∂z较小,即溶液无限稀]或扩散系数的浓度变化率较小[∂D(C)/∂C~0]的条件下,D值可看作是与浓度无关的常量D0,因此式(2)可以简化为 (3) 在初始条件与边界条件下, (4) 将上式代入式(3),C(z,t)可以用误差函数[erf(ζ)]表示为 (5) (6) 已知C1,C2和C(z,t)=Cc,式(6)中的反误差函数有明确的数值,令其为a,则式(6)可简写为 (7) (8) 比较式(7)和式(8)即可求出扩散系数D0. 基于液芯柱透镜的实验测量装置如图2所示. 激光器发出的单色光束(λ=589 nm)通过准直扩束系统(由显微物镜、针孔滤波器[13]及球面透镜组成)和限宽狭缝后,进入消球差液芯柱透镜,经柱透镜折射后,在其焦面上形成束腰状的扩散图像,并由图像采集系统(CMOS相机)记录成像. CMOS的分辨率为4 096×4 096 pixel,像元尺寸为4.5 μm×4.5 μm. 消球差液芯柱透镜置于半导体温控装置内,透镜及扩散溶液的温度控制在室温(25.0±0.1) ℃条件下. 图2 实验装置图 1)用型号为FA2004的电子天平(上海舜宇恒平科学仪器有限公司)称量葡萄糖样品,用EU-LS-100TJ型超纯水器(南京欧铠环境科技有限公司)产出的去离子蒸馏水配置不同物质量浓度的葡萄糖水溶液. 将浓度为Ci(i=1,2,…,n)的葡萄糖水溶液依次注入液芯柱透镜的液芯区,当单色准直光束通过柱透镜后,移动CMOS相机分别测量出其准确成像的位置Xi(i=1,2,…,n). 采用多项式拟合法确定成像位置Xi与浓度Ci之间的函数关系X(C). 2)用数字注射泵在柱透镜芯区下方注入初始扩散浓度为C2的葡萄糖水溶液,注入时保证溶液没有沾在透镜上半部分的内壁上,注入后静置10 min以消除注入溶液的湍流. 用注射泵以0.25 mL/min的速度沿透镜内壁缓慢地将相同体积的去离子蒸馏水(C1=0)注入到透镜上方,定义2种溶液刚接触的时刻为扩散过程的初始时刻(t0=0). 3)根据实验需要,选择扩散溶液中的等浓度薄层,由拟合的X(C)函数关系可计算出单色准直光束通过此薄层后在CMOS芯片上清晰成像的位置Xc,利用位移平台将CMOS相机移动并固定在Xc位置上. 为减小注液时的湍流对扩散造成的影响,及保证半导体温控装置的稳定性,扩散开始20 min后,需每隔120 s采集记录1幅扩散图像. 配置了16组葡萄糖水溶液,其物质量浓度为Ci,将不同浓度的葡萄糖水溶液分别注入液芯柱透镜芯内,测得准直光束在CMOS芯片上的准确成像位置Xi,如表1所示. 分别用1次、2次和3次曲线拟合法确定成像位置Xi与浓度Ci之间的函数关系. 经过对比发现,3次曲线拟合的相关系数最高,R2=0.999 9,故本文通过3次曲线拟合结果确定X(C),如式(9)所示,其反函数如式(10)所示. X=5.8C3-1.9C2-15.92C+41.42, (9) C=-0.000 1X3+0.013X2-0.57X+9.3. (10) 在液芯柱透镜的下方注入初始浓度为C2=1.000 mol/L的葡萄糖水溶液,上方注入C1=0 mol/L的去离子蒸馏水,选择能够清晰成像浓度为Cc=0.084 mol/L的等浓度薄层. 根据式(6)可计算出a=0.975. 表1 不同浓度葡萄糖水溶液的成像位置 表2对应的扩散图像随时间的变化规律如图3所示,图像束腰位置(图中箭头所指位置)随时间的演变过程,能够可视化地表现出微观分子的扩散运动. 这是本实验可以形象化地观察扩散过程的独特优势. 表2 葡萄糖水溶液扩散过程中束腰位置随时间的变化 图3 CMOS采集到的不同时刻的扩散图像 等浓度薄层的选择和液芯柱透镜的焦深是影响扩散系数测量的2个主要因素,下面对其进行分别讨论. 为确定合适的等浓度薄层Cc值,在初始扩散浓度取固定值C2=1.000 mol/L的条件下,选择不同等浓度薄层,重复2.2节描述的实验步骤,扩散系数D0的测量值随Cc值的变化如图4所示. 图4表明,D0随Cc值的增加而变大,但在Cc小于0.1C2后,D0趋于稳定. 图4的曲线变化规律反映了式(3)的成立条件,即小浓度差近似条件. 在Cc≤0.1C2后,小浓度差近似条件得以满足才可以运用文中的式(3)~(7),所以,Cc≤0.1C2可以作为本实验Cc值的选择条件. 初始扩散浓度C2也可能是影响测量结果的因素. 为确定C2对测量结果的影响,在等浓度薄层满足Cc≤0.1C2的条件下,选择初始浓度不同的(C2=1.000, 1.500, 2.000 mol/L)葡萄糖水溶液重复2.2节描述的实验步骤,测量结果如表3所示. 结果表明,选择不同的C2值,测得D0值基本稳定,可见测量结果与葡萄糖水溶液的初始浓度无关. 图4 扩散系数D0的测量值随Cc的变化 此外,当确定C2值,分别选取3个不同的Cc值时,D0的测量结果也基本稳定,进一步验证了Cc≤0.1C2可以作为Cc值的选择条件. 表3中9组扩散系数的平均测量结果为D0=(1.156±0.029)×10-5cm2·s-1,与文献[14]中的测量值接近. 在成像系统的焦平面附近,探测器非失真成像所允许调节的间距就是系统的焦深[15]. 焦深是影响扩散系数测量的另一因素. 对比式(7)和式(8),扩散系数可以表示为 (11) 式中,k是式(8)拟合得到的斜率值,在相关系数R2=0.998 1的条件下,液相扩散系数的测量误差(ΔD0)主要由a的偏差值(Δa)导致,进而由等浓度薄层的浓度偏差值(ΔCc)确定. 根据式(10),等浓度薄层焦点位置(Xi)的不确定量(ΔXi,焦深值)决定了浓度偏差值ΔCc,即: (11) 表3 初始扩散浓度(C2)与等浓度薄层(Cc)对测量结果的影响 根据以上分析,对不同等浓度薄层(Cc)的焦点位置(Xi),测量了对应的焦深值(ΔXi);根据焦深值ΔXi,分别计算了偏差值ΔC,Δa和ΔD0,计算结果如表3所示. 通过计算,可以得出焦深造成的扩散系数偏差值在10-8cm2·s-1量级. 本文基于消球差液芯柱透镜搭建了光学检测系统,采用等浓度薄层移动测量法,在室温下测量了葡萄糖水溶液的液相扩散系数,测量结果为D0=(1.156±0.029)×10-5cm2·s-1,与文献测量值接近. 此外,本文还研究了不同浓度的等浓度薄层对扩散系数的影响,结果表明:当所选等浓度薄层满足Cc≤0.1C2时,则小浓度差近似条件成立,扩散系数测量值趋于稳定;在研究初始扩散浓度对扩散系数的影响时,发现扩散系数测量值与初始浓度无关;在研究液芯柱透镜的焦深对扩散系数测量的影响时,得到焦深造成的扩散系数偏差值在10-8cm2·s-1量级. 等浓度薄层移动测量法具有实验装置和操作简单、测量结果可靠、扩散过程可视化等特点,为物理、化工、生物、医疗等领域对扩散系数的测量提供了新的有效手段.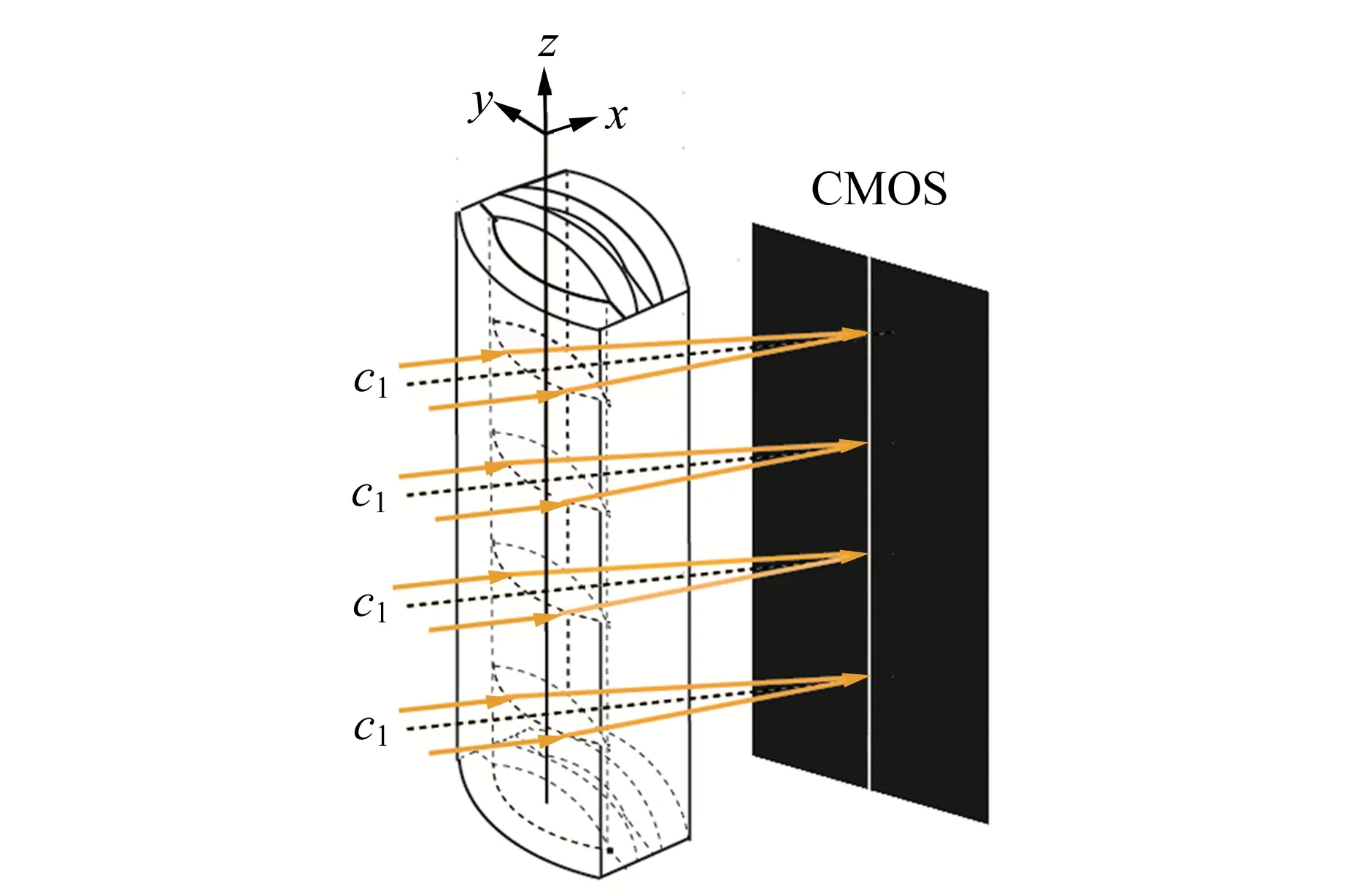

1.2 计算理论

2 实验内容
2.1 实验装置
2.2 实验步骤
3 实验结果及分析
3.1 X(C)及C(X)函数关系的确定
3.2 实验结果

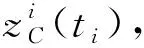

3.3 实验结果影响因素分析

4 结 论

