散射透镜的成像原理及应用

谢向生,魏 洁,梁浩文,刘忆琨,周建英

(1.汕头大学 物理系，广东 汕头515063；2.中山大学 物理学院，广东 广州 510275)

1 散斑相关成像发展概况

当光束通过非均匀介质后，光场的振幅和相位(波前)空间分布被打乱，导致光的传播方向发生改变，这种现象叫做光的散射. 光所通过的非均匀介质统称为散射介质，散射介质在日常生活中很常见，例如雨雪雾霾、生物组织、毛玻璃，甚至1张白纸都可以被看作散射介质. 当散射介质复杂度增加时，其透射光线的空间分布、偏振状态以及频率都会发生改变. 散射现象的存在会使物场发出的同源光束无法重新会聚，干扰成像过程，降低图像的信噪比，因此大多数情况下，光的散射被认为是图像产生噪声的主要原因之一，极大地影响了物体的成像质量，需要被滤除. 由于大多数场景均存在散射介质，克服散射影响的成像恢复在日常生活、科研、安保和军事中均有广泛的应用需求.

随着研究的深入，研究人员发现，虽然散射介质会干扰光场，但散射介质在一定条件下呈现类似透镜的物理特性，因此，称之为散射透镜. 虽然透射光场形成空间“混乱无章”的散斑或“均匀”的背景，但仍然携带物场的本源信息，通过先进成像技术，例如计算成像技术(Computational imaging technology，CIT)[1]，可将其用于成像恢复. 有别于传统光学成像的“所见即所得”，计算成像技术是充分利用信息获取和计算处理的成像方式. 随着新型传感器性能的多样化、计算机计算能力的提升以及算法的智能化，计算成像技术打破了传统光电成像技术对成像过程的分立式表征，以全局观点描述整个光学成像过程，综合考虑照明、光传输、光探测、数字图像处理和显示等过程. 全光参量信息(或称光场全要素)[2]记录与重现也逐渐成为研究人员关注的重点问题.

借助计算光学成像，利用混乱光场(或光强)分布进行成像恢复已经取得了系列成果. 其中散斑相关成像技术因所需条件简单(只需采用非相干光照明)，且具有成像质量高、恢复速度快、易于集成等诸多优点，受到了研究人员的关注[2]. 2012年，J. Bertolotti等人利用激光器在散射介质前面进行高精度扫描采集散射图像，并利用迭代算法对其进行恢复，实现了非接触式的成像恢复[3]. 2014年，Ori Katz团队采用非相干光照明，仅利用1张物体的散斑图重建出了物体的强度图[4]. 2016年，Y. Park等人提出了基于散斑相关散射矩阵的无参考光全息相机，实现了无参考光的全息成像[5]. 同年，中山大学周建英团队将解卷积技术应用到成像恢复，得到了实时、彩色、大视角和超分辨的成像恢复结果[6].

2018年，N.Antipa等人[7]利用特制的准散射体实现了无透镜散射相机. E.Valent等人[8]发现不同散射介质有其特定的散斑谱，可以利用神经网络进行机器训练，并且用线性区分算法进行识别. 2019年，美国波士顿大学V.Goyal团队[9]仅用1台普通数码相机拍摄墙上模糊不清的光影，结合遮挡物评估算法实现了视线外(Non-line-of-sight，NLoS)成像. 上海光学精密机械研究所韩申生团队基于光场高阶关联优化和相位共轭实现了透过散射体的双向成像[10]，司徒国海团队利用已知物的辅助实现了透过散射介质的成像[11]. 西安电子科技大学邵晓鹏团队在透散射介质的计算成像方法和水下偏振成像技术研究方面取得多项成果[12]. 清华大学戴琼海、金欣团队利用散斑相关技术实现了散斑评估[13]和超过光学记忆效应范围的物体自动恢复[14]. 国防科技大学陈平形、刘伟涛团队在二阶关联的抗散射光学成像方面,结合解卷积算法实现了运动物体的实时成像[15]. 哈尔滨工业大学赵远团队提出时间直方图解卷积方法，实现了高分辨的NLoS成像[16]. 深圳大学彭翔团队采用改良的相位迭代算法实现了散斑相关成像恢复质量的提升[17]. 上海交通大学曾贵华/石剑虹团队提出了高效有限光子相关成像技术[18](快速第一光子鬼成像). 中国科学技术大学袁仁民团队在大气边界层物理、大气湍流等方面有深入的研究[19]. 龚雷团队实现了光场透过散射体的三维聚焦[20]. 西安交通大学朱京平团队在偏振成像方面(宽波段、光谱特性建模分析、混浊介质中偏振成像等)[21]开展了探索工作.

散斑相关成像恢复技术正在蓬勃发展，探索散射介质的物理性质成为成像恢复技术的关键. 本文从常规的正透镜入手，介绍其物理结构和傅里叶变换特性；引入散射介质的记忆效应和散射透镜概念，介绍其在结构特性、变换特性以及具有代表性的成像恢复研究方面的应用.

2 透镜的傅里叶光学特性

透镜是成像系统中最重要的元件，忽略吸收和界面反射等光损耗，透镜的主要功能是波前相位变换. 透镜能将平行或发散光会聚，在其后焦面上可以观察物体的夫琅禾费衍射，也就是对入射场进行了傅里叶变换[22]. 相反，透镜也能对物场的空间频谱进行傅里叶变换，得到物体的像. 透镜的2个基本性质——聚焦和傅里叶变换器(包括成像)，使其成为光信息处理最基本、最重要的元件.

2.1 透镜的透过率函数

当光线水平入射到凸透镜上，入射波的波前各点在透镜上都受到了正比于厚度的相位延迟调制. 在薄透镜近似下，透镜近轴的透过率函数可以表示为

(1)

表示光波通过透镜上(x,y)点时，产生的相位延迟与该点到透镜中心的距离的平方成反比，同时也与透镜的焦距f有关[23-24].

2.2 正透镜的傅里叶变换特性和条件

透镜具有对自由空间传播物光场进行傅里叶变换的特性. 标准的点光源不易实现，而平行光则相对容易获得. 当不限定物体和观察平面的位置时，菲涅耳衍射会产生二次相位因子项[25]，包括与透镜坐标无关的衍射项以及依赖于透镜坐标的相位项. 只有这些项被消除，透镜才能直接对入射场进行傅里叶变换，简化相关计算.

采用平行光照明时，在3种情况下，物场的二次相位因子可以被忽略，光路如图1所示，此时透镜能对入射场直接进行傅里叶变换.

(a)

(b)

(c)图1 用正透镜进行傅里叶变换的光路

1)物体位于以光轴和透镜的交点为球心，以z1为半径的球体表面上,图1(a)所示.

2)在对具体像点(x,y)处的场有重大贡献的物场区域内，二次相位因子的相位变化远远小于这个区域，如图1(b)所示.

3)物由会聚的球面波照明，会聚点是光轴和透镜的交点，此时会聚的球面波刚好与上述的二次项因子抵消，如图1(c)所示.

上述3个条件只需满足其中1个，二次相位因子就可以被消去. 消去透镜的二次相位因子的作用，也称为透镜定律[25]. 上述3种情况实际上是共轭光路的3种特例.

2.3 正透镜的点扩展函数及聚焦特性

在信息光学或傅里叶变换光学中，点扩展函数(Point spread function，PSF)定义为满足空间平移不变性的线性系统对δ函数的脉冲响应，反映了光学系统的成像对应关系：

h(xo)*o(xi),

(2)

其中,g(xo)表示像场分布，o(xi)表示物场分布，下标i和o分别表示输入和输出，光学上可以描述为物和像. 线性算符L表示光场的可叠加性.xi′表示统一的坐标宗量(例如在光学成像系统中是输出平移除以放大率)在输入空间任选的一点，从而可以用h(xo)表示系统的PSF. 当光学成像系统的PSF确定，也即点光源的像确定，则成像可以分解成多个物点所成的多个PSF光斑的叠加；当2点的像光斑距离小于光斑尺寸时不可分辨，可以推知PSF的大小正好用来描述光学成像系统的分辨率.

空间平移不变性在光学系统中有限定条件，以标量场为例，Kirchhoff衍射公式能求解传统的衍射问题，但是，倾斜因子K(θ)破坏了空间平移不变性，需要采用一定的近似(如傍轴近似)才能将其作为常量，得到标量形式的PSF并用于描述菲涅耳衍射和更远距离的夫琅禾费衍射. 此时，像可以看作物和PSF的卷积，也就是说，PSF是标量场衍射问题在傍轴近似下的合理近似.

引入PSF极大方便了光学成像系统的理论描述，一方面可以直接把系统当作进行卷积运算的黑箱，不用逐个分析光学元件对光场的具体影响；另一方面可以通过模拟整个成像过程的理论描述求解系统的PSF，从而推测出任意输入光对应的成像结果. 此外，PSF在空间频域的描述为光学传递函数(Optical transfer function,OTF)，输入光的频域分布乘以OTF得到输出光的频域分布，这在信息光学研究中有广泛的应用.

透镜的PSF的求解模型如图2所示[26]，以任意取向的偶极子μ为点源，通过高数值孔径物镜进行准直，形成平行光束. 平行光束被透镜聚焦所形成的焦场分布则为系统的PSF. 当平行光束尺寸大于透镜孔径时，则焦场分布为透镜的PSF，因此透镜的PSF能够描述其聚焦特性.

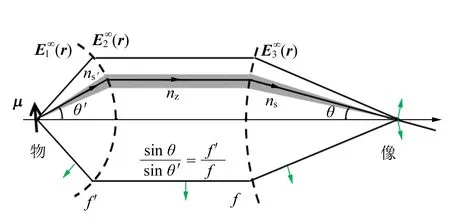
图2 透镜PSF的计算模型

大部分教科书描述透镜聚焦也是采用平行光照射透镜，分析其聚焦光场分布，或者如图1(a)的情况，直接对透镜孔径函数进行傅里叶变换.

紧聚焦情况下计算透镜的PSF，可以采用矢量衍射理论. 结合近期多参量光场调控的新型光场调控技术的进展[27]，采用矢量光场可以更严格地描述光场在多参量调制下的传播、紧聚焦以及结构光场与物质相互作用的行为. 矢量光场的独特性质在生物光子学、量子信息、光学显微成像、近场光学、光学微操控、激光加速和激光直写等领域具有巨大的应用价值，并已经逐渐被研究人员开发出来.

(3)

其中Ω为透镜收集的立体角，可通过调整环形光阑改变角度θ的积分区间. 推导过程需要利用消球差透镜的正弦条件和强度法则，如图3所示.

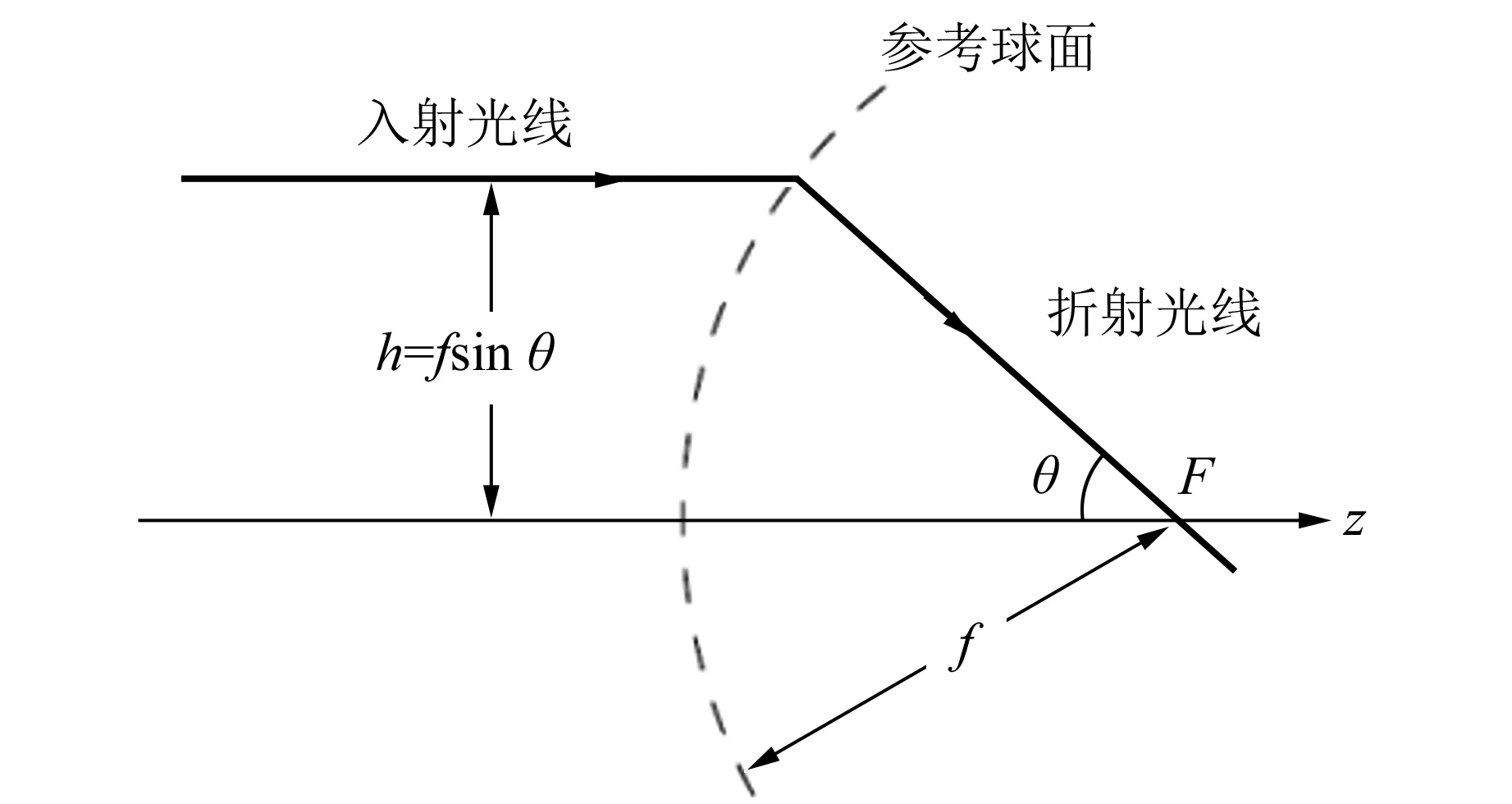
(a)正弦条件

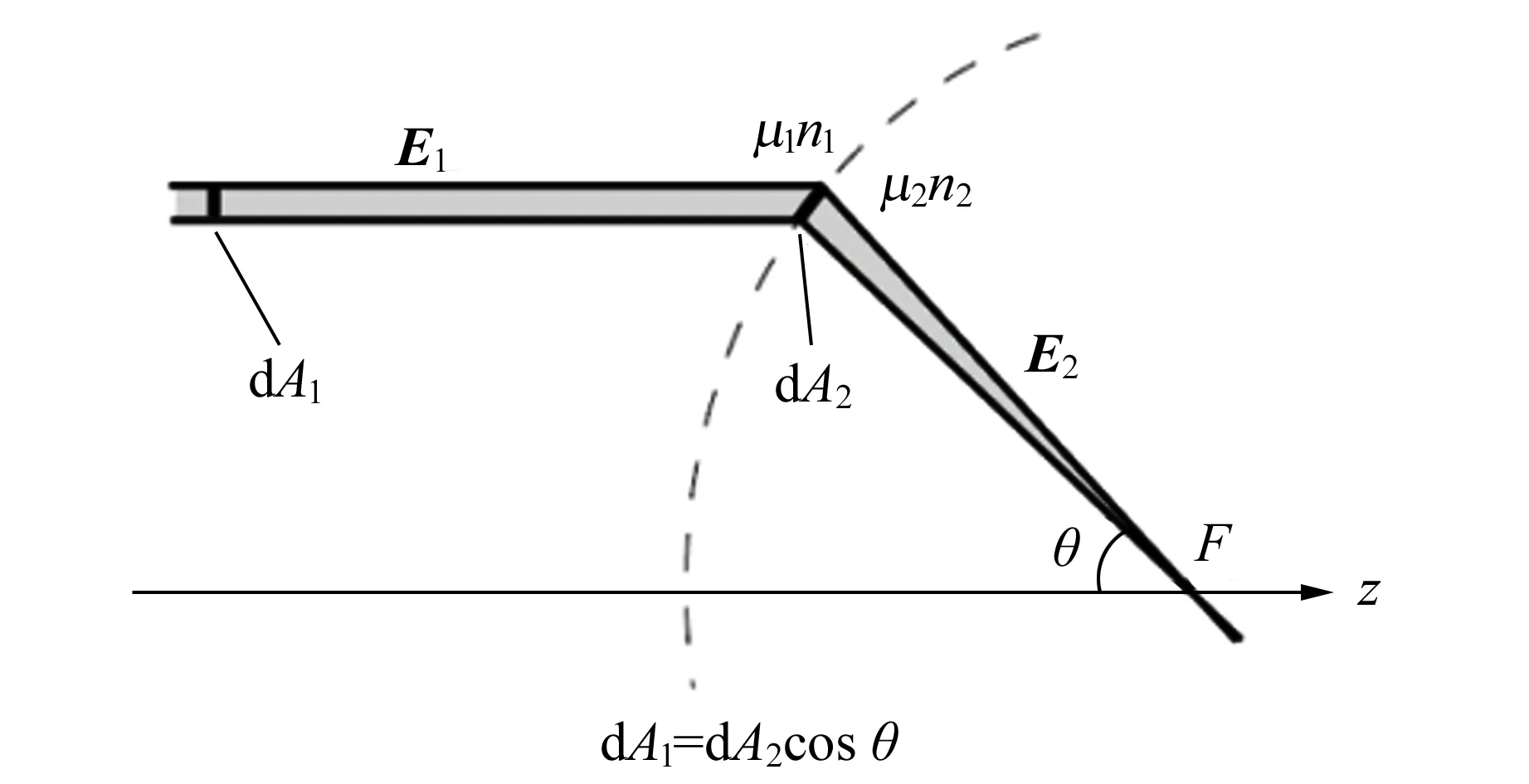
(b)强度法则[26]图3 消球差透镜的2个重要性质

如图2设定偶极子的振动方向是x，强度为μx，求出在像面上的傍轴PSF为[26]

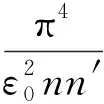
(4)

(5)

同理，可以求出轴向的PSF为

(6)

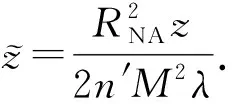
(7)

3 散射介质的光学特性

任何线性光学系统均可以采用传输矩阵来描述，当散射介质可以简化为线性系统时，则可以采用传输矩阵测量法进行测量. 此时传输矩阵用来描述散射体出射光场和入射光场之间的数学变换关系，是非常巨大的三维矩阵. 2010年，法国朗之万研究所S.Popoff小组首次对散射体传输矩阵进行了测量[30]，利用散射体的传输矩阵实现了对散射出射光场任意控制，并通过散射光场实现成像恢复[31]. 2011年，韩国首尔大学Choi小组测量了散射体在空间频率域的传输矩阵[32]，并实现了透过散射体的超分辨成像恢复[33]. 此外，光声效应以及波前调控技术也被用于测量散射体的传输矩阵[34-35]. 传输矩阵测量法的测量过程需要采集大量的输入光场和输出光场数据，再进行计算. 散射介质受到散射体的光学记忆效应限制，因而并非是完全的线性空不变系统. 当散射介质很薄时，可以用空间随机相位函数来表示. 根据散射介质颗粒度的大小，可以设置随机函数的像素尺寸(也可以用相应半高全宽的高斯函数与随机函数进行卷积).

3.1 散射体的光学记忆效应和散射透镜

当散射介质的光学厚度比较薄时，通常认为光通过介质平均只有1次散射，该散射介质的透过率函数的相位项可以用随机函数Rand(x,y)和高斯函数Gauss(x,y)的卷积来表示[36]：

ts(x,y)=exp [-iRand(x,y)*Gauss(x,y)].

(8)

该式比透镜的透过率函数[式(1)]复杂，但仍然满足空间平移不变性.

散射介质对透过的光波有记忆效应,具体表现为：光波透过散射介质后，在其对应的像平面上产生散斑. 散斑是由于散射介质的折射率分布不均匀，光束通过散射介质后形成的随机交替的亮斑和暗斑[37-38]. 在图像恢复中散斑常被认为是杂乱无序、不携带信息的噪音. 近年来的实验研究表明，散斑分布虽然看似杂乱无序，但仍有某种特定的分布特征，这种分布特征就是散射系统的PSF，可以在一定程度上反映散射系统的光学成像特性. 即散射介质在特殊情况下具有类似透镜的成像特性，被称为散射透镜.

散斑会受多种因素的影响，因此改变实验条件后产生的新散斑与原来的散斑不同. 但是由于记忆效应，入射光的角度在一定范围内(较小偏转角度)发生偏转时，散斑的强度与偏转之前相比不会发生很明显的变化. 随着入射角度的改变，散斑图案会随之产生一定的平移，即散射体的光学记忆效应. 记忆效应在1988年被加利福尼亚大学Feng等人首次提出[39]. 同年，以色列I. Freund等人通过实验证明了这一现象的存在[40]. 实验证明，记忆效应的范围仅与散射介质的厚度L有关，转动前后散斑之间的关联函数为

(9)

式中q=2π/λ,λ为入射光波波长，L为散射介质的厚度. 随着L的增加，记忆效应存在的有效范围会减小.

记忆效应的定量测量示意图如图4(a)所示. 实验中的散射体是美国Newport公司生产的标准散射体套装中的80°聚碳酸酯全息散射片. 准直扩束后的激光照射在散射体上，激光透过散射介质后，被散射体后方的CCD接收. 当激光的入射角度偏转Δθ时,在CCD上可以同步观察到散斑的移动. 图4(b)是氦氖激光偏转Δθ=36,72,110 mrad时的散斑. 对散斑的细节进行放大可看出，偏转角度较小时(如Δθ=36,72 mrad)，形成的散斑与0 mrad的散斑几乎相同，无变化;偏转角度Δθ=110 mrad时，形成的散斑与0 mrad的散斑有很大的差异. 用相关系数可以定量地描述不同偏转角度散斑之间的相似程度. 某个Δθ下的散斑与0 mrad散斑的相关系数定义为两者散斑图像互相关的最大值：max[corrx (A,B)][40]，如图4(c)所示. 从图4(c)曲线可以看出，散斑相关系数随着偏移角度的增大而逐渐减小，当Δθ=80 mrad时，相关系数降低为1/2. 由于对称性，认为在Δθ=±80 mrad的范围内，散斑与原点的散斑相同，此范围也称为记忆效应的有效范围.

(a)实验示意图

(b)不同偏转角度下的散斑图以及局部放大图

(c)偏转后散斑相关性与偏转角度的关系图4 散射介质偏转角度相关性验证实验

角记忆效应虽然被证实存在，但是由于其对应的有效范围角度太小[约为λ/(2πL)]，很难被广泛应用到散斑相关成像恢复技术. 2015年，Judkewitz等人在角记忆效应的基础上提出了平移光学记忆效应[41]，解决了有效范围角度小的难题. 平移光学记忆效应是当入射光平移时，透过介质后的出射光也随之平移，平移前后的散斑同样具有很强的关联性. 因此平移记忆效应能应用于厚散射介质和整个空间充满散射介质的情形，拓展了散斑相关成像的应用范围和场景.

3.2 散射体的“聚焦特性”和分辨率

光场经过散射介质时，会发生随机的反射、折射过程，所以散射光场的具体表现形式和光场分布形式难以用理论推导或数值模拟的方式来探究. 为了更好地研究散射过程，需要从统计的角度给出物理描述，称为散斑统计或散斑统计光学. 通常对散射光场给出如下假设[37]：

1)散射光场的相位φn与散射光场的振幅an是统计独立的；

2)相位φn的随机过程满足(-π，+π)之间的均匀分布.

基于以上2个假设下的光场随机游走过程，将导致散射光场中光强I满足负指数统计分布，即光场中某点光强为I的概率为

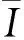
自相关通常用于描述信号的周期性，表示为1个信号平移Δx后与原来信号之间的相关性，数学上对信号q(x)的自相关定义为

对于绝对随机的噪音信号q(x)，任何Δx≠0的平移信号与其本身的相关系数都为0，唯有平移量Δx=0时相关系数为1，即随机噪音的自相关是狄拉克函数，可以从白噪音的功率谱分析得到.

完全散射光场的自相关可以从散射体背面到散射空间的菲涅耳衍射进行推导. 推导中假设靠近散射体背面光场的自相关是狄拉克函数. 而在远场衍射下散射光场的自相关却不再是狄拉克函数，其具体形式与散射体表面形貌有关[37]. 例如，对于有效的散射面为l×l的矩形散射体而言，散射光场的强度自相关为

(10)

其中，λ是输入光场的波长，z是距离散射表面的垂直距离. 对于有效散射面为直径D的圆形散射体而言，散射光场的自相关为

(11)

(a)矩形散射片

(b)圆形散射片图5 散斑自相关横截图[37]

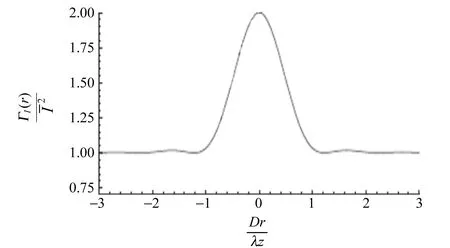
2种形状散射片形成的散斑横向自相关函数ΓIr(Δx,Δy)与ΓIc(Δx,Δy)分布相似，包含背景常量和峰函数2部分. 峰函数与衍射极限有关，当l或者D很大时峰函数会退化为极窄的狄拉克函数. 当l或者D很大时，散斑光场的自相关函数可以近似为ΓI(Δx,Δy)=δ(Δx,Δy)+c,其中c为背景常量. 这个近似是所有散斑解自相关技术的理论基础[2-4]. 由于散射成像是基于散斑的相关性来实现，散射透镜的成像分辨率等价于散斑的颗粒度或散斑自相关的半高全宽. 比较式(4)和式(11)，透镜对平行相干光场聚焦形成的横向焦场和散射体形成散斑的横向自相关具有几乎一致的形式(除了均匀背景常量)，因此其分辨率也具有相同的半高全宽. 同时散斑自相关轴向的分布函数，以圆形和方形为例，分别表示为

(12)

(13)

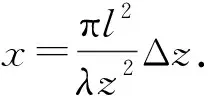
ΓIc(Δz)和ΓIr(Δz)分别为以均匀照明的直径为D的圆形和l×l的方形散射面形成散斑的自相关. 比较式(6)和式(12)，透镜对平行相干光场聚焦形成的轴向焦场和散射体形成散斑的轴向自相关具有一致的形式，除了常量项外连，均匀背景常量也消失了. 均匀背景消失的原因在于轴向散斑的缩放特性导致互相关为0.

4 散射透镜成像方法和特性

由于存在记忆效应，散射成像系统可以看作是线性平移不变系统，散射体后形成的散斑是物体与散射透镜PSF的卷积，成像是通过散斑的相关性来实现.

当光透过散射介质后，在像面上产生的图像由艾里斑转变为散斑，即PSF也会在像面上表现为散斑图，该散斑在一定范围内具有平移不变性. 当入射光不是点光源时，可以把入射光源看作无数个点光源的叠加，对应的PSF(散斑)也可看作是这些点光源所对应的PSF(散斑)的叠加. 而整个成像的过程就可以看作是系统总的PSF和物函数进行了1次卷积. 此过程可以表示为

O(xo,yo)dxodyo]，

(14)

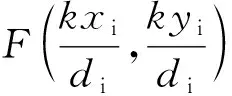
(15)

式中，a和b表示2个不同的取样位置，Δqa和Δqb分别表示出入射波的波矢差，其中Δqa=ka-ka′，Δqb=kb-kb′，L是散射体的厚度. 由式(15)可知，F函数是类钟形状的角度函数，仅当物体在记忆效应范围内时，它们才能有相同的散斑图案，散斑相关成像特性也只在此范围内成立. 因此F函数决定散射系统视场的大小[42-45].F函数与散斑之间的关联函数C[式(9)]具有相似的形式，前者是2个平移物点的散斑互相关，后者是同一物点转动散射介质后的互相关，因此形式相似.

4.1 基于解卷积的散射透镜成像方法

基于散射透镜的成像光路如图6[7]所示. 为了实现散射透镜成像恢复，需要散射透镜的PSF和物光场通过散射透镜后的散斑分布. 这2个数据反映到实验中为点光源的散斑分布和物体经非相干光照射后的散斑分布. 最常见的做法是用CCD分2次采集获得，如图7所示.

用点光源(一般为非相干光源，如LED)照射针孔(通常要求针孔直径小于散射透镜的分辨率为20～200 μm)来获得PSF. 由于散射作用，入射光经过散射介质后分布范围会大大增加，而CCD孔径有限，如图6(a)所示，大部分的散斑无法被采集用于成像. 为了解决这一问题，庄辉昌等人提出了双透镜系统[6]，即在原有的光学系统中再引入2个透镜，如图6(b)所示. 一个透镜放在散射介质前，收集非相干光用于散射成像；另一个透镜放在在散射介质后，收集散斑光传给CCD. 这种方法不仅能提高系统的视场，还能大幅提升散射光场的相关性.

(a)常规的散射透镜成像系统

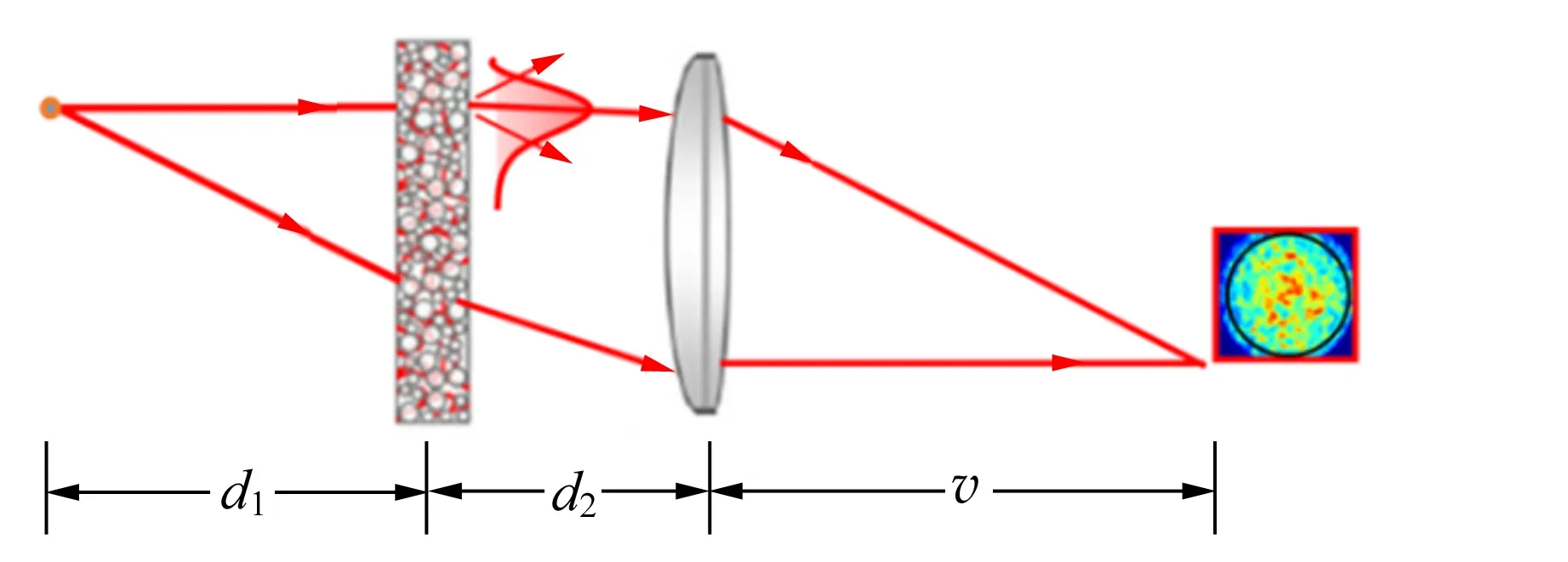
(b)视场扩大的散射成像系统图6 常规与视场扩大的散射成像系统的对比(图中白圈表示出瞳，黑圈表示视场范围，红框表示CCD芯片区域)

图7 基于解卷积的散射成像恢复步骤

综合考虑不同算法恢复图像的信噪比和算法运行时间，维纳滤波解卷积是比较有效的方法[46]，可以表示为

(16)

其中,I和PSF分别是未知物体的散斑和点扩散函数，F{·}是傅里叶变换操作. 从式(16)可知实现解卷积运算只需要进行2步傅里叶变换：矩阵除法和傅里叶逆变换. 离散傅里叶变换具有高效、快速的算法计算库，而且傅里叶变换和矩阵除法都采取并行计算实现. 利用GPU并行计算，不考虑CCD图像采集和GPU启动过程的时间消耗，对2 048×2 048原始图像进行图像恢复，实测进行1次图像恢复只需要1～3 ms的时间. 这相比于先前工作中图像恢复的时间(自相关成像恢复3 s，波前整形30 min)，解卷积法在速度上具有质的飞跃，可以实时地进行透过散射介质成像. 这为实时散射成像提供了可能，例如生物组织动态过程的观察、安防实时监控等.

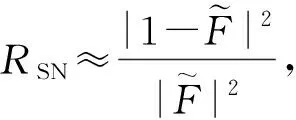
4.2 散射透镜的放大倍数

成像系统的放大系数是很重要的参量，对于焦距为f的单透镜成像而言，利用高斯公式：

(17)

图8 基于解卷积的散射成像恢复

4.3 散射透镜的轴向特性

与传统透镜不同，散射透镜的焦距不是固定的，虽然是由式(17)定义，但是散射透镜的物距与像距不像传统光学透镜具有严格的一一对应关系. 传统透镜的f固定，物距确定，像距也会随之确定，但是对于散射透镜来说，物距和像距在一定范围内可人为决定，因此其焦距也会随着物距和像距的变化而发生改变.

对于固定的散射体，位于其特定深度的PSF(对应于坐标中的z轴)只能用来恢复该深度平面上的物体图像，无法恢复出其他深度的清晰物体图像. 为了实现更大景深范围内的成像，需要获得相应深度的PSF. 如果每个深度的PSF都要通过测量获得，会导致人力、物力消耗过大，其应用场景也会受到限制. 为了解决这些问题，谢向生等人[44]发现对于同一散射介质，不同深度的PSF之间具有很大的关联性. 在已知散射介质某一深度处的PSF之后，可以通过缩放因子m推导出其他深度的PSF. 2个点扩散函数之间的关系式为

(18)

当物体轴向移动时，散斑需要通过缩放才能保持其关联性，因此如式(11)和(12)，当不对散斑进行缩放操作时，散斑的互相关没有均匀的本底背景，这个现象与散斑横向平移不同.

4.4 散射透镜的波长特性

相似地，不同波长情况下的PSF之间也有关联. 当未知物体的散斑光谱和已知PSF的散斑光谱有重叠时，二者之间存在串扰效应，所以二者的PSF之间也具有一定的关联性，因此利用已知波长情况的PSF能推导出其他波长情况下的PSF. 2个PSF之间仍然由缩放因子m联系，其关系为

(19)

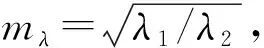
(20)

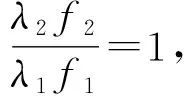
5 结束语

本文从透镜的物理结构和傅里叶变换特性出发，描述了传统光学透镜的基本结构和聚焦特性. 与之对比，提出了散射介质的一般结构及其光学表征方法. 由于透过散射介质的光场满足光学记忆效应，形成的散斑具有空间平移不变性，利用光场相关运算，散射介质具有如同透镜的成像特性，被称为散射透镜. 着重介绍了基于散斑相关的解卷积成像恢复方法及具有代表性的研究方法和实验系统. 讨论了解卷积滤波器的设计方法，分析了散斑轴向的相关性，以及不同光谱散斑的相关性方法. 虽然本文介绍的散射透镜成像原理不够完善，且目前这一方法在实际中的应用仍有较多困难，但散斑相关成像仍然是非常具有发展前景的成像手段.