基于EMD-EWT的回转窑故障识别研究
张 云,毛 达
(武汉理工大学 机电工程学院,湖北 武汉 430070)
回转窑是一种在水泥、冶金、化工等领域应用广泛的大型设备,其主要由筒体、大齿圈、托轮、轮带等组成。由于窑受温度变化、物料旋转、不当操作等因素的影响,窑筒体会出现不同类型的故障,这些故障会在其支撑托轮上有所反映,导致托轮受载异常,甚至导致轴瓦异常发热,引发窑的停产事故。因此,通过对托轮位移信号监测,及早发现回转窑故障,对保证设备安全具有重要意义。
目前回转窑故障识别最新研究主要包括:张云[1],Zheng K[2]建立托轮的振动模型,解释其内在振动机理,并通过实验指出筒体谐波(kiln harmonic, KH)与托轮谐波(roller harmonic, RH)是反映筒体弯曲与托轮受力状况的主要成分。秦岭[3]、胡昭中[4]、卢振东[5]以及胡航宇[6]分别采用了双树复小波变换(dual-tree complex wavelet transform, DTCWT)、完全集合经验模态分解(complementary ensemble empirical mode decomposition, CEEMD)、变分模态分解(variational mode decomposition, VMD)、经验小波变换(empiricsal wavelet transform, EWT)用于提取托轮位移信号的特征谐波,并取得一定进展。但是上述4种方法均存在一定不足:DTCWT算法滤波器构造困难。CEEMD本质上是一种噪声辅助算法,对第一类模态混叠有一定抑制作用,但其噪声幅值系数与集总次数设置困难,文献[4]以原始信号与重构信号的相关系数、均方差和信噪比作为分解评价指标的方法并不具有普适性。此外,当托轮位移信号成分中包含筒体二倍频时,托轮转率与筒体二倍频之间的频率比约在1.5左右,采用CEEMD算法处理托轮信号会出现第二类模态混叠问题,使该方法失效。VMD算法模态个数与惩罚函数两个参数设置困难,文献[5]采用的以能量差与正交性指标的参数优化方法只对特定托轮信号有用,且该方法参数优化计算时间过长,不适合回转窑实时监测场合。文献[6]采用EWT提取KH与RH,但未能考虑现场低频趋势项对傅里叶频谱的干扰,且以人为观察频谱峰值个数的方式来设置算法中分量个数,方法自适应差。
因此,针对现有托轮位移信号处理方法的不足,笔者提出一种结合EMD与EWT的回转窑故障特征提取方法,并以KH与RH的能量作为窑故障程度的评价参数。通过处理实际托轮位移信号,验证了所提方法的有效性。
1 回转窑故障监测原理
文献[1-2]研究表明,托轮振动位移信号中的KH与RH频率成分分别是反映筒体弯曲故障与托轮受力状况的特征频率。图1(a)为回转窑状态监测示意图,通过数据采集仪器监测回转窑各托轮位移信号,可实时反映回转窑的运行状态。图1(b)为某挡托轮位移信号监测原理示意图。轮带由对称分布的两个托轮支撑,霍尔开关安装在筒体某处来测量筒体的旋转周期,电涡流位移传感器安装在沿轮带与托轮接触点延长线上,测量托轮位移信号。则由轮带直径、托轮直径、筒体周期算得筒体频率fS与托轮频率fR为:
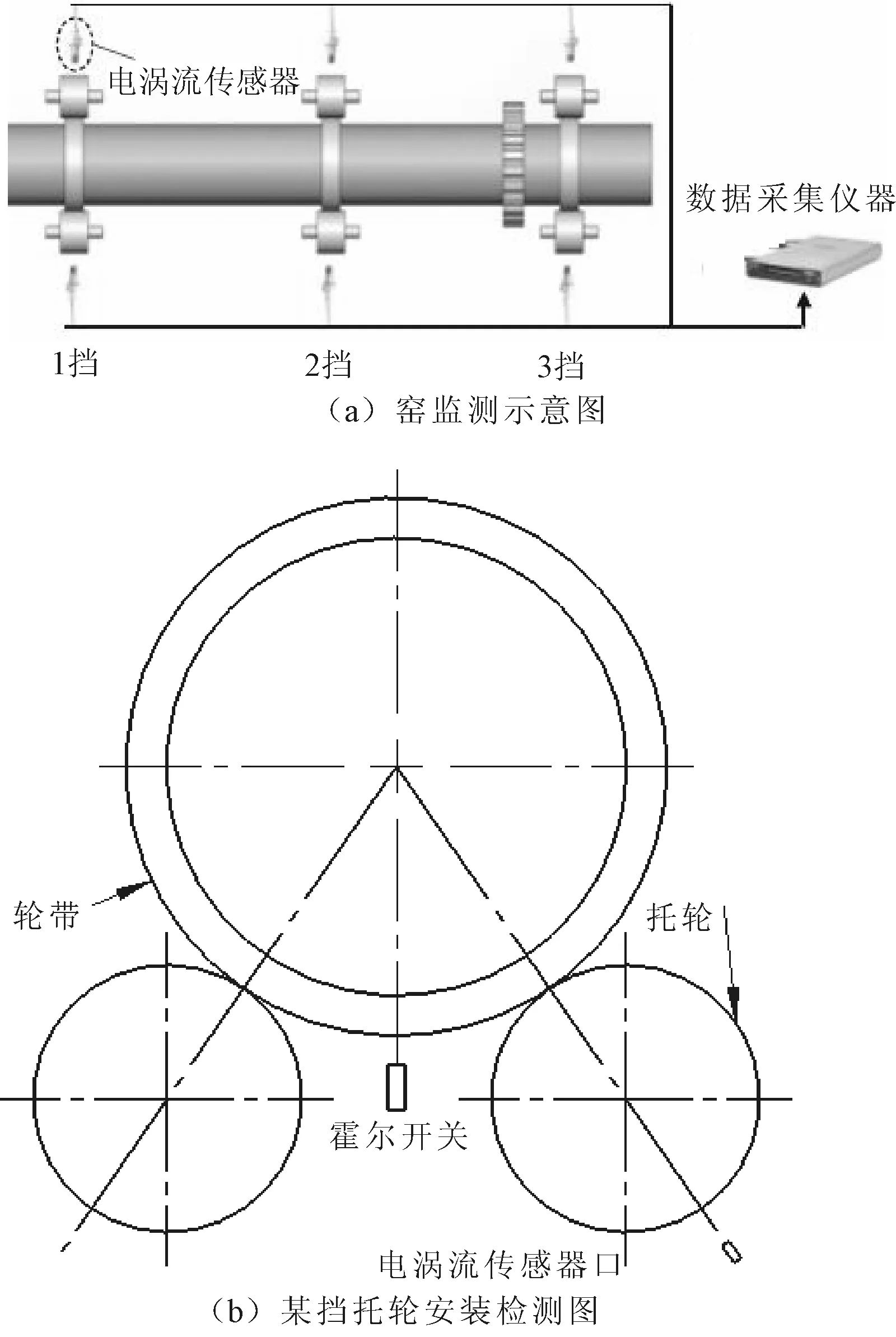
图1 窑托轮位移监测示意图
(1)
式中:T、DS、DR分别为筒体周期、轮带直径、托轮直径。
2 基于EMD-EWT的回转窑故障特征提取原理
2.1 基于EMD托轮位移信号趋势项去除原理
EMD是一种基于数据本身驱动的信号分解算法,可将非平稳信号分解为若干个固有模态函数(intrinsic mode function, IMF)与一个余量。任意IMF需满足以下两点:①在整个数据系列中,极值点的数目与过零点的数目必须相等或者最多相差一个;②由局部极大值点与局部极小值点所构成的包络线的均值都等于零。EMD算法主要流程如下:
(1)求解信号x的局部极大值与局部极小值,以三次样条函数拟合极值点序列,形成上下包络线。
(2)计算上下包络线均值m1,计h1=x-m1。若h1满足IMF两个条件,则h1为第一个IMF;反之,执行步骤(3)。
(3)以h1代替x,顺次执行步骤(1)和步骤(2),直至第k次结果h1k满足IMF两个条件,则将h1k作为第一个IMF,记为c1。此步骤中,k次循环停止条件可采用标准差系数SD准则或者三参数准则[4]。
(4)计算r1=x-c1,并以h1代替x,执行步骤(1)~步骤(3)。则有r2=r1-c2,…,rn=rn-1-cn且当rn单调即可结束。则x为ci(i=1,2,…,n)与rn之和。
回转窑工业现场恶劣,实际采集的托轮位移信号往往出现较为明显的趋势项。由于采用的EWT算法涉及对信号的傅里叶频谱分割,若对信号中的趋势项不加以抑制,会使傅里叶频谱低频段出现较大误差。因而有必要对托轮信号进行趋势项抑制的预处理操作。传统的趋势项提取方法如最小二乘法、小波变换法等均存在一定不足,如最小二乘法需要事先知晓趋势项的形式,小波变换法需要选择合适的小波函数[7]。EMD算法因其自适应的特点可以更好地提取趋势项,因而采用EMD算法提取趋势项,并通过过零检测法判断各固有模态函数(IMF)是否为趋势项组成成分。过零检测法充分利用了趋势项振荡缓慢的特点,具有稳定性好、速度快的特点[7]。托轮位移信号趋势项去除具体流程为:
(1)对托轮位移信号执行EMD过程,得到若干个IMF。
(2)从低频IMF开始进行过零检测,得其零点个数。若零点个数不高于指定阈值,则说明该分量为趋势项组成成分。针对托轮位移信号,由于趋势项为低频成分,阈值N0可按照经验公式(2)确定:
N0=floor(L/(2FsT))
(2)
式中:L与Fs分别为托轮位移信号的长度与采样频率;floor表示向上圆整。
(3)重复(2)过程,当首次出现零点个数超过指定阈值时,即可停止检测。将已检测出的IMF相加即为提取的趋势项。
(4)将趋势项从原始托轮位移信号减去即可得去除趋势项后的托轮位移信号。
2.2 基于EWT的回转窑故障特征提取原理
EWT由Gilles结合经验模态分解与小波分解各自优点提出的自适应非平稳信号处理方法。其基本原理如下:
(1)将信号的傅里叶频谱划分为M个连续的区间,令fm(m=0,1,…,M-1)表示每个区间的界限,f0=0、fm=π,每个片段以及整个频谱区间表示为:
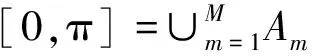
(3)
(2)在每个子区间上,依据式(4)~式(5)构造经验尺度函数和经验小波函数:
(4)
(5)
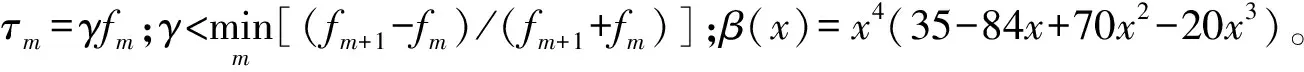
(3)通过式(6)计算细节系数;通过式(7)计算逼近系数;通过式(8)重构信号。则分解的经验模式分量通过式(9)得到。
(6)
(7)
(8)
x(0)=W(0,t)×φ1(t)
xk(t)=W(k,t)×ψk(t)
(9)
由EWT原理可知,该算法的关键在于如何划分信号的傅里叶频谱。Gilles提出的方法是通过比较傅里叶频谱局部极大值的幅值,进而确定频谱分割区间[8]。但是当故障特征频率幅值比干扰成分频率幅值低时,Gilles提出的方法就无法保证一定能够对故障特征频率所在区间进行合理划分。笔者通过对比采集的多组现场实验数据发现,托轮位移信号的频率成分按照频率由低到高主要包括:趋势项低频干扰成分、筒体转频成分、筒体转频二倍频成分、托轮转频成分、托轮转频倍频成分以及高频干扰成分。因而,根据上述托轮位移信号的成分特点以及由式(1)计算的筒体频率fS与托轮频率fR,对托轮信号傅里叶频谱进行如下分割:
Fseg={0.5fs,1.5fS,(2fS+fR)/2,1.5fR-fs}
(10)
式中:Fseg为傅里叶谱分割线位置集合。其中,前3个分别以0与fS、fS与2fS、2fS与fR各自的中点位置为分割线位置,而最后一个分割线与fR距离等于第3个分割线与fR距离。
采用该方法按式(10)对去除趋势项后的托轮信号傅里叶频谱进行分割,然后执行EWT算法的剩余步骤即可分解出故障特征谐波KH与RH成分。笔者并非根据整个频谱的局部极大值信息来确定分割线位置,而是根据窑故障频率成分将其分割为固定的5个子区间,因而自适性强。
3 基于EMD-EWT与特征谐波能量的窑故障识别实验
3.1 托轮信号趋势项去除实验
为验证EMD算法用于去除托轮信号趋势项的有效性,笔者采用广东省某水泥厂5 000 t/天回转窑实际测量数据。现以该窑1挡右侧托轮位移信号s作为分析对象。其相关参数如表1所示。

表1 被测回转窑相关参数表
信号s原始波形及其EMD结果如图2所示。由图2可知,s被分解成8个IMF与1个残余量。其中,第8个IMF的零点个数为6,第7个IMF的零点个数为11,残余量的零点个数为1。而根据式(2)确定的阈值N0为7。故可认为,残余量与第8个IMF共同组成趋势项成分。从s中减去提取的趋势项,可得其去除趋势项前后对比图,如图3所示。图3(a)为原始信号s及提取的趋势项,图3(b)为去除趋势项后的波形图。由图3(a)可知,提取的趋势项较好地表征了信号的整体趋势,说明采用EMD提取托轮位移信号趋势项是可行和有效的;由图3(b)可知,去除趋势项后,信号平稳性明显增加。
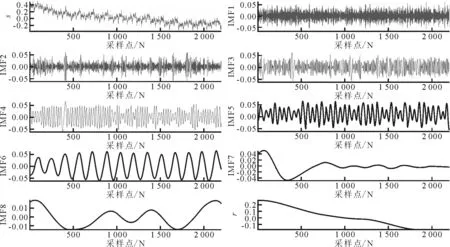
图2 托轮位移信号EMD结果图
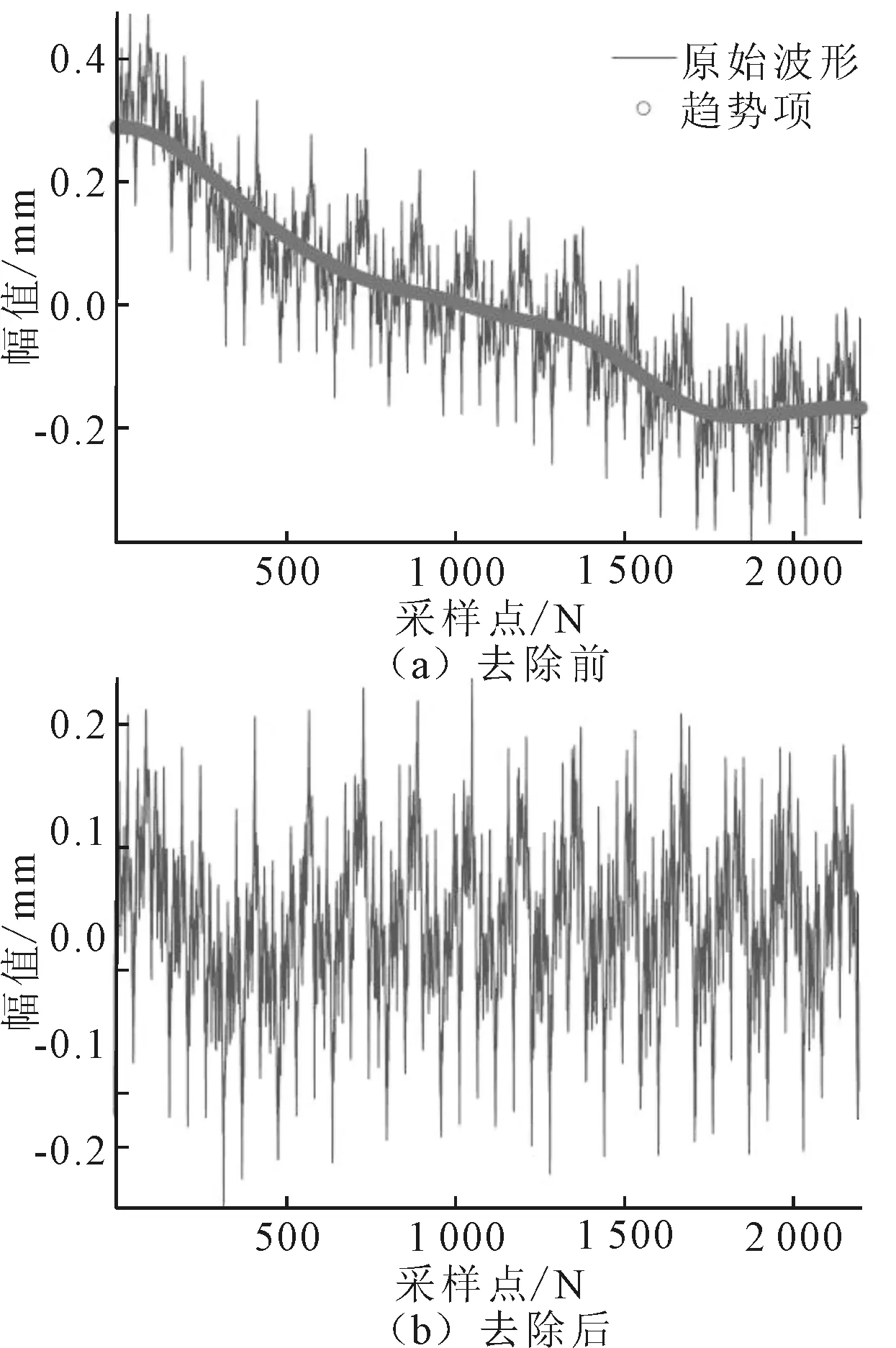
图3 托轮位移信号趋势项去除前后时域对比图
为对比去除趋势项前后的低频段信号对傅里叶频谱的影响,下面给出信号s的傅里叶频谱对比图,如图4所示。由图4(a)可知,二者在大于1 Hz的频谱段几乎相同,这是由于去除的趋势项成分以低频为主;由图4(b)可知,去除趋势项后的托轮位移信号频谱比未去除之前的波动更小、干扰成分更少,故障特征频率谱峰更为突出,且频率越低抑制干扰效果越好。

图4 托轮位移信号趋势项去除前后频域对比图
3.2 回转窑故障特征提取实验
由表1和式(1)可知筒体周期为15.7 s,托轮周期为5.3 s,即筒体转频fS为0.063 7 Hz,托轮转频fR为0.188 7 Hz。则按照式(3),将信号傅里叶频谱分割成5个区间,结果如图5所示。由图5可知,故障频率所在区间被有效划分,说明所提出的方法具备可行性。图6为其分解后的各分量的时域图及对应的频谱图。所提取的故障特征谐波KH、RH分别对应为第2个、第4个分量。KH频率值为0.063 69 Hz与0.063 7 Hz基本一致,RH频率值为0.186 5 Hz与0.188 7 Hz也基本一致。由此可知,笔者提出的特征谐波提取方法可以有效分离出KH和RH成分。
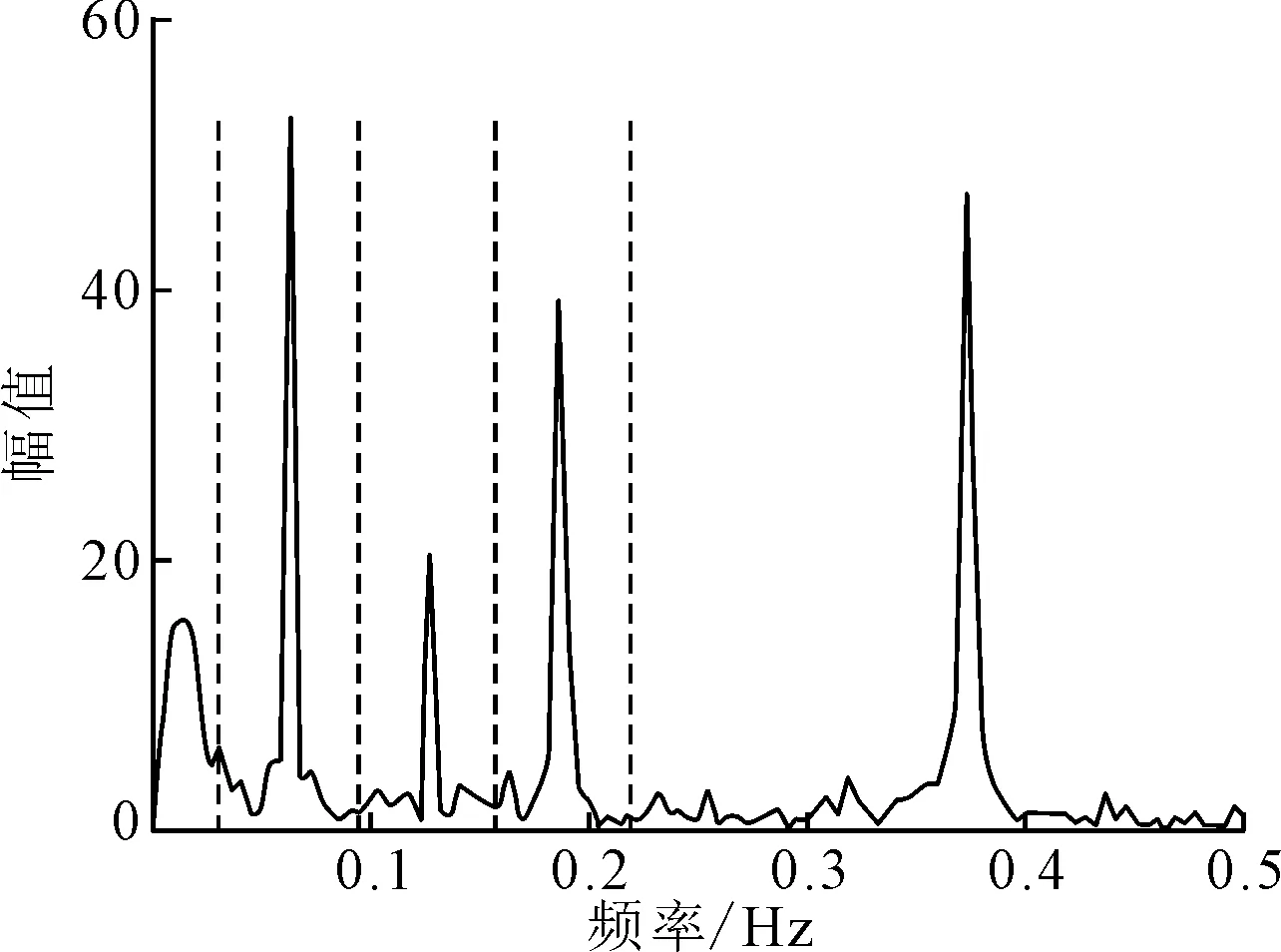
图5 EWT频谱区间分割图
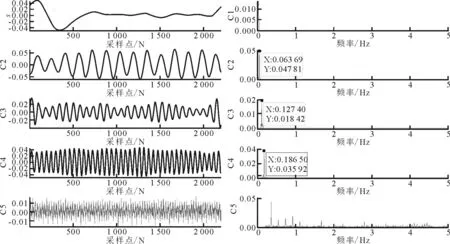
图6 EWT分量提取图
3.3 基于特征谐波能量的窑故障识别实验
采用上述EMD-EWT方法对该窑各挡托轮位移信号进行处理,提取各自对应的KH和RH,并按式(11)计算KH和RH的能量,将二者能量作为反映窑故障程度的评价指标。
(11)
式中:E为能量;L为信号长度;c(k)为KH或者RH成分。
各挡位KH能量对比图如图7所示,由图7可知:1挡、2挡KH左右侧能量平均值基本相等,且二者均大于3挡左右侧KH能量平均值,说明1挡、2挡筒体弯曲比3挡严重。该窑同时用窑弯曲测量系统测得各挡附近筒体截面偏心值[9],其结果如图8所示。由图8可知,1挡、2挡偏心值基本一致,且二者均大于3挡,说明1、2挡筒体弯曲比3挡严重。因此,采用KH能量可有效反映筒体的弯曲故障程度。
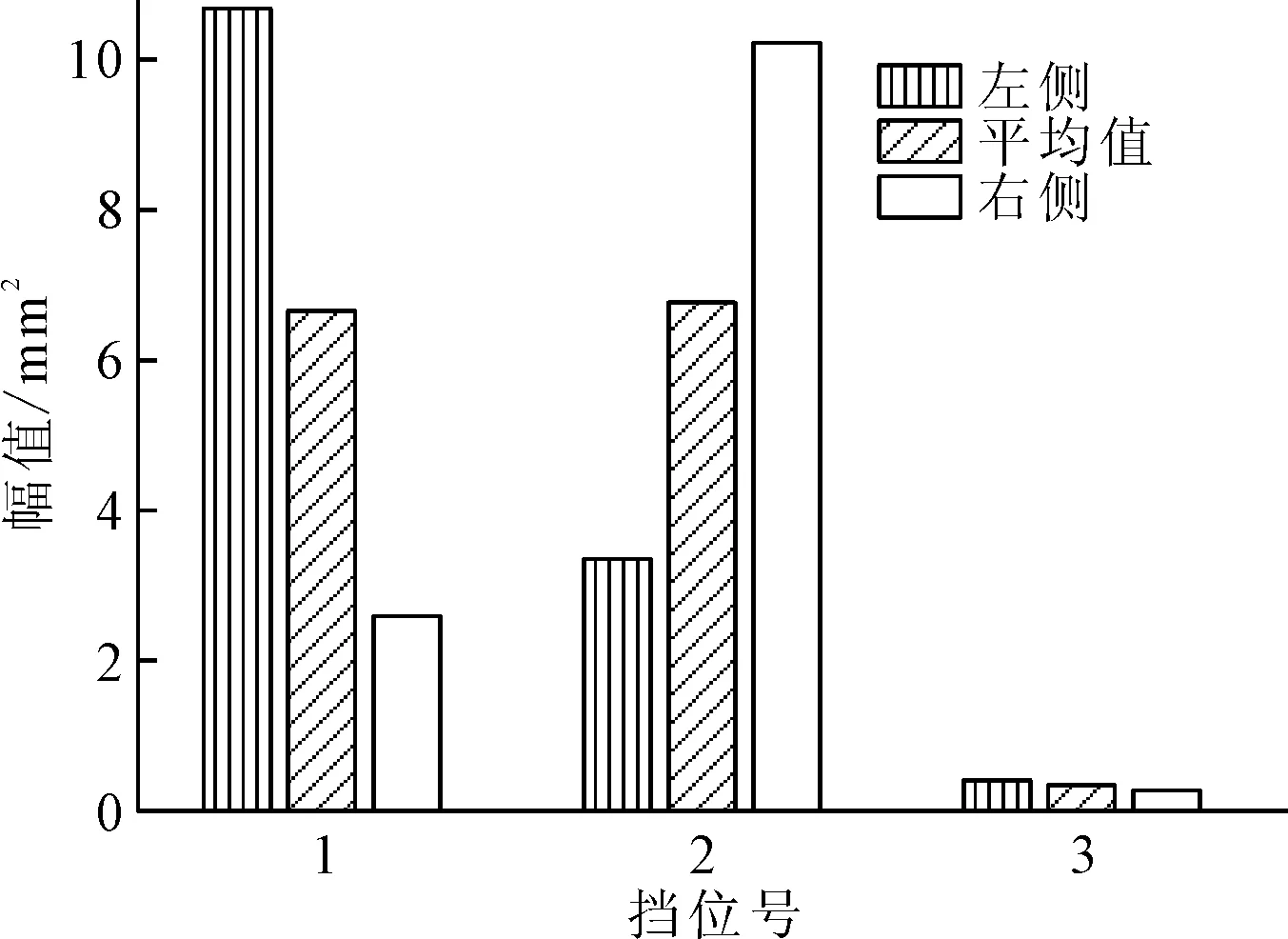
图7 各挡KH能量对比图
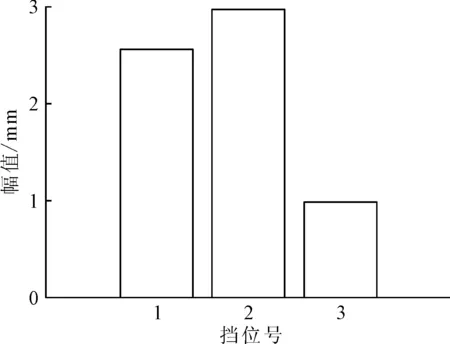
图8 各挡截面筒体偏心值对比图
各托轮RH能量对比结果如图9所示,由图9可知,3挡左托轮RH能量值大于右托轮,但二者能量差不多,说明该挡左托轮受力大于右托轮,但二者受力比相差不大。采用椭圆度仪器[10]测量筒体各截面的椭圆度曲线,结果的局部放大图如图10所示。图10中所示波峰与波谷间距值L与R比值反映各挡左右托轮受力大小比例,L>R说明左托轮受力大于右托轮。则据此可知,该窑3挡左托轮受力大于右托轮;由于L与R相差不大,说明左右托轮受力差异不严重。1、2挡分析类似,不再赘述。因而,托轮RH能量值可有效反映各挡左右托轮受力状况。
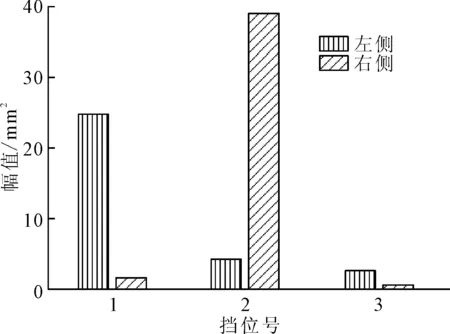
图9 各挡左右托轮RH能量对比图
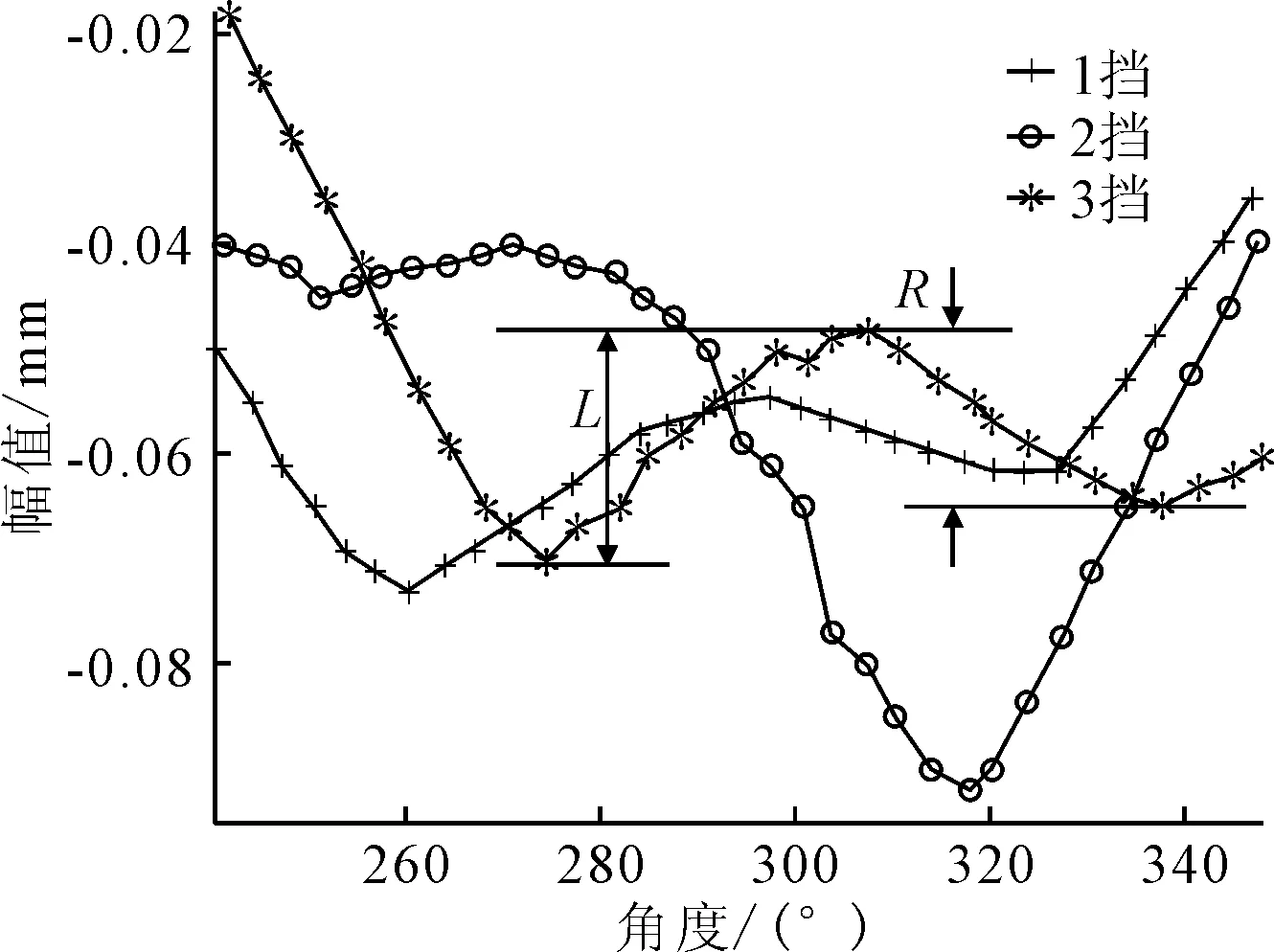
图10 各挡位筒体椭圆度曲线图(局部)
4 结论
笔者提出一种基于EMD-EWT和特征谐波能量的回转窑故障识别方法,为回转窑故障实时监测提供了一个新的解决方案。主要结论如下:
(1)结合EMD与零点检测方法可有效提取托轮位移信号中的低频干扰成分,抑制其对回转窑故障频率的干扰,使故障频率谱峰更为突出。
(2)依据托轮位移信号频率成分特点及事先计算出的筒体转频fS与托轮转频fR,可大大简化EWT算法的频谱分割过程,节省计算时间,使EWT能够准确提取出KH与RH成分。
(3)采用KH与RH的能量作为评价参数可以分别反映筒体弯曲和各左右托轮受力状况及故障程度。

