铅酸蓄电池逆向物流库存模型

李 根

(武汉理工大学 机电工程学院，湖北 武汉 430070)

铅酸蓄电池是化学电池中市场份额最大，使用范围最广泛的电池[1]。事实上，超过80%的铅蓄电池只有一到三年的寿命[2]。据不完全统计，国内每年有大约300到400万吨的铅酸蓄电池报废，并且每年增长率维持在15%左右[3-4]。通常，废旧铅蓄电池包含大约70%的铅板、20%的酸液，其余的是塑料[5]。通过对铅酸蓄电池的回收处理，可以延长电池的生命周期，提高铅等资源的利用率，提高电池企业经济效益，保护环境。库存管理是废旧电池回收处理过程中的重要环节，优秀的库存管理策略既可以保障废旧电池正常回收，还能降低处理成本。

国内外很多学者针对逆向物流的库存管理问题进行了大量的研究。Alamri[6]统一考虑新产品和再制造产品库存，建立了包含3种库存的库存模型。Corum等[7]针对混合制造和再制造库存系统进行研究，对比4种不同库存控制策略情况下库存成本的变化。ZHU等[8]研究逆向物流选择不同时需求出现不同的定值情境下的库存管理模型。刘志峰等[9]，针对废旧家电产品，建立基于PULL策略的逆向物流库存控制模型。

在铅蓄电池逆向物流回收方面，国内外学者大多数研究回收网络的规划构建。Subulan等[10]基于模糊条件，建立了一个多目标，多层次和针对多个产品的MINLP(mixed-integer nonilinear programming)模型。Garg等[11]依据不同的分配方法，建立了模拟印度北部地区的废旧铅蓄电池的回收正逆双向物流模型。郭雄[12]根据铅蓄电池回收流程和回收模式，构建铅蓄电池回收网络，建立逆向物流回收中心选址模型。

综上所述，国内外学者在铅蓄电池回收问题上多是研究电池回收网络布局，较少研究电池回收企业的库存问题。笔者以获得最小平均总成本为目标，根据PULL策略，以市场需求率为主要因素，建立多种因素影响的废旧铅酸电池逆向物流库存模型，具体研究具有再生铅功能的铅酸电池生产企业回收处理过程中的库存问题。结合具体案例，求解模型的最小平均成本和周期，同时分析主要参数对目标函数的影响。

1 模型建立

1.1 PULL策略概述

依据逆向物流再利用方式的分类方式，把废旧铅蓄电池的回收处理过程分为再利用和再生处理过程。根据回收的电池来源，分为废弃回收和其他方式(退货等)。再利用处理过程指回收的小部分电池经过简单修复就能够恢复电池功能，重新进入市场，修复工艺相对简单，耗时比较短；再生过程是指为了获得再生铅和塑料等材料，并对硫酸合理处理进行的拆解和制造新电池过程。在工厂建立3个库存点：电池回收品库存、再生材料库存和铅酸电池成品库存。电池回收到工厂后，首先进行质量检验，然后分为不同种类进入电池回收库存，等待再利用和再生处理。经过处理并且通过检验的电池进入铅酸电池成品库存，准备进入市场。图1废旧铅酸蓄电池再利用/再生工艺流程。

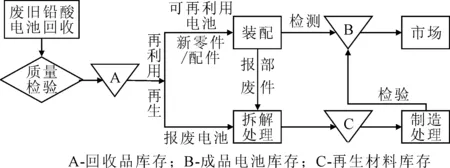
图1 废旧铅酸蓄电池再利用/再生工艺流程

根据PULL策略，分析废旧铅蓄电池到达工厂后存储、再利用和再生过程。把工厂回收的电池数量作为数据输入。市场对成品铅蓄电池的周期性需求来推动模型的运行。工厂接收到市场周期性订货指令后，分类处理回收的电池，并且电池的回收数量和市场需求量相关。图2为再利用/再生PULL控制策略模型。

图2 再利用/再生PULL控制策略模型

1.2 模型设计

模型中变量和参数说明如下:

再利用/再生的PULL策略库存模型如图3所示，电池市场每隔周期T发出需求量为D的订货指令。接到指令后，工厂第一步检查成品库中电池数量，如果超过D，则立即出货；否则，工厂对回收的电池进行再利用或再生处理。

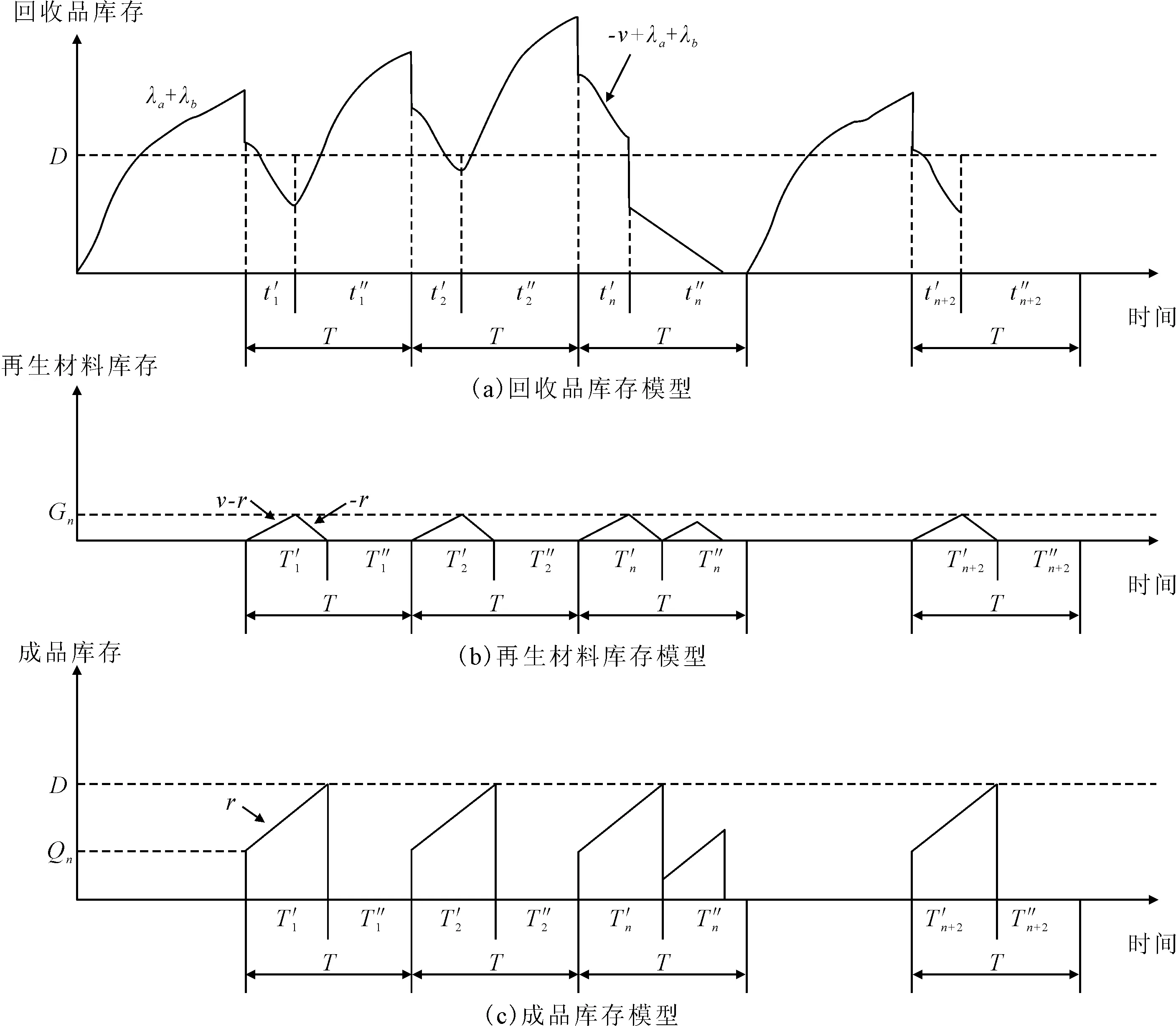
图3 再利用/再生的PULL策略库存模型

在T′i时间内，工厂以v的速率拆解电池，以r的速率制造成品电池，其中v>r。并且这段时间内一直回收废旧电池，回收品库存电池数量以λa+λb-r的速率增加，成品电池的数量以r的速率增加。在T′i结束时刻，成品电池数量达到D，结束再利用和再生处理。对此时的回收品库电池数量进行检查，如果需求量大于废旧电池数量，则继续回收；反之，立即停止回收，直到下一周期重新恢复回收，并且不停止处理，一直到回收品库电池数量变为0。

工厂会优先进行再利用处理，再利用处理的电池全部转变成成品后，如果成品数量小于D，剩下的需求量由再生处理来满足。经过Ti′再生处理过程全部完成后，以D为单位统一出货。依据PULL策略建立铅酸电池逆向物流库存模型，需要进行以下假设：

(1)电池通过废弃回收和其他方式(退货等)回收，两种方式相互独立;

(2)回收速率λ服从泊松分布，回收速率与市场需求速率相互独立；

(3)可回收电池数量很大，能满足市场需求；

(4)再利用处理电池，可以获得和再生处理相同的品质；不考虑再利用处理时间，在周期开始时瞬间完成，电池进入成品库；

(5)电池的处理符合“先进先出”原则；

(6)成品电池数量达到D，立即出货；

(7)主要考虑3种库存的固定成本和可变成本，两种处理成本；

(8)拆解过程中酸液无害处理后会运至下游企业处理。因此，只考虑再生电池可回收比例部分的处理费用；

(9)周期性盘点3种库存数量；

(10)接到市场订货指令开始计算周期。

1.3 模型建立

设第一个周期回收品库初始库存为：

E1=Q=(λa+λb)T

(1)

第一个周期T完成可再利用电池数量为：

(2)

第一个周期T可再生电池数量为：

(3)

第一个周期开始时再生材料库存为0。

第一个周期T需要制造电池的数量为：

(4)

第一个周期需要制造处理的时间为：

T′1=S1/r

(5)

第一个周期需要拆解处理的时间为：

t′1=S1/v

(6)

第一个周期经过T′1剩余可再生数量为：

(7)

B′1=(λa+λb)T′1

(8)

M′1=L′1+B′1

(9)

B″1=(λa+λb)T″1

(10)

第二个周期回收品库初始库存量为：

E2=M′1+B″1

(11)

那么，可以推导出第n个周期回收品库初始库存量为：

En=M′n-1+B″n-1

(12)

t′n1=[L′n+(naλa+nbλb)T′n]/v

(13)

需要制造处理的时间为：

t′n2=[L′n+(naλa+nbλb)T′n]/r

(14)

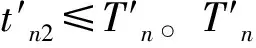
(15)

第n个周期结束后，回收品和再生材料库存数量为0。n+1个周期组成一个循环总周期。第n+1个周期继续回收电池，但不处理新回收的电池，结束时回收品库存为：

En+1=(λa+λb)T

(16)

前n-1个周期内，0～t′i时间段内，再生材料库存随时间变化关系为：

G′i=(v-r)t

(17)

t′i-T′i时间内，再生材料库存变化为：

G″i=(v-r)t′i-r(t-t′i)

(18)

T′i时刻后到周期结束库存为0。

第n个周期0～t′n1时间，再生材料库存变化与公式(17)相同。t′n1～t′n2时间内，再生材料库存变化与公式(18)相似，将t′i换成t′n1即可。t′n2时刻到周期结束库存为0。

第i个周期T′i时间内回收品库存成本为：

(19)

T″i时间内回收品库存成本为：

(20)

前n-1个周期T回收品库存成本为：

(21)

第n个周期T回收品库存成本为：

(22)

第n+1个周期T回收品库存成本为：

(23)

前n个周期T再利用处理总成本为：

(24)

前n个周期T制造处理总成本为：

(25)

前n个周期T拆解处理总成本为：

(26)

前n-1个周期T成品库存总成本为：

(27)

第n个周期T成品库存成本为：

(28)

前n-1个周期T再生材料库存总成本为：

(29)

第n个周期T再生材料库存成本为：

(30)

将n+1个周期的处理成本，以及3个库存产生的库存成本相加得到总成本。n+1个周期后，回收品和再生材料库存回到初始状态，求出平均总成本。通过建立模型，将研究铅酸电池逆向物流库存问题转化成平均总成本的优化问题。在符合下面5个约束条件的基础上，求得最优解，得到最佳库存控制策略。目标函数为：

(31)

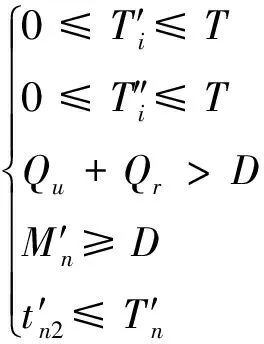
1.4 模型求解

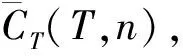
图4 优化方法流程图

(1)给定初始解T=T0，n=n0，确定T、n的步长分别为δ1和δ2(大于0)；

(3)判断n+δ2是否满足约束，满足则n=n+δ2返回第二步；否则T=T+δ1,n=n0，返回第二步；

(4)当满足终止条件时，输出最优解。

2 算例和参数分析

以襄阳某家废旧铅酸电池处理企业为例，使用模型和优化方法求解。企业给出参考数据如表1所示。通过计算，得到T=3.5，n=4时模型最优，平均总成本最小为36 721元。在第4个周期结束处理时，回收品库电池数量超过市场需求量，停止回收。5个单位周期组成一个总周期，共17.5天。总周期内共回收18 375台电池，通过再利用处理得到2 450台，再生处理获得12 382台。

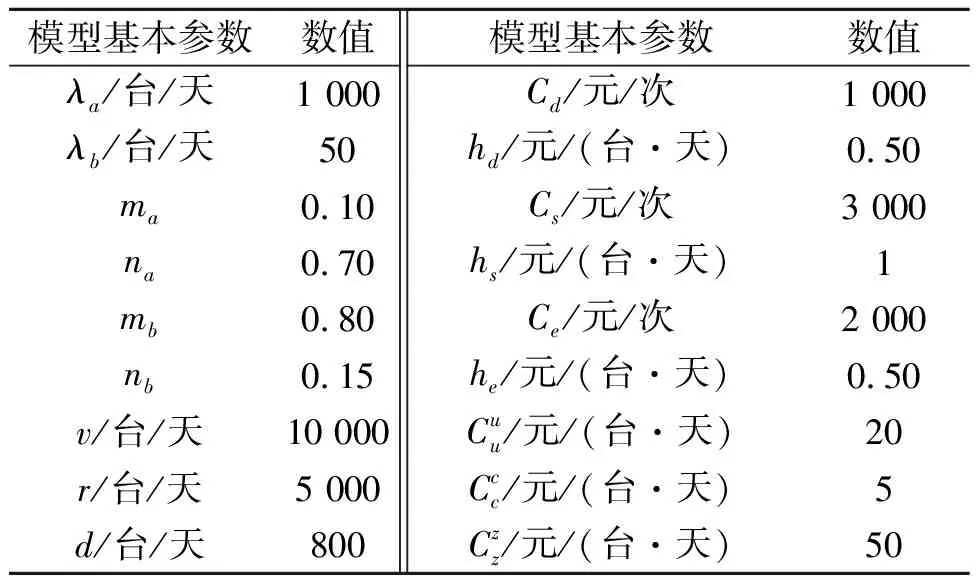
表1 PULL策略下的基本参数

模型中参数n不仅与T有关，也与电池回收数量、处理能力、可再利用/再生比例有关。下面以周期最优解T=3.5来研究其他几个参数变化对平均总成本影响。

(1)再生过程中制造新电池速率r和电池拆解速率v对平均总成本的影响。r会改变制造处理时间T′n的大小，影响3个库存点单位周期成本，导致平均总成本变化。v会直接影响拆解时间t′n的大小，影响回收品库存和再生材料库存成本大小，导致平均总成本变化。如图5所示，r在0～8 000台/天之间下降非常迅速，在8 000台/天之后下降趋于平缓，说明r对平均总成本影响变小。v对平均总成本影响开始时有一个上升过程，后面一直下降，但影响范围很小。

图5 平均总成本随r和v的变化

(2)回收的电池中，废弃回收的电池占大部分，因此主要分析废弃回收的电池中可再利用比例ma和可回收比例na的变化对平均总成本的影响。图6为4种再生电池可回收比例下，随着ma增大，平均总成本的变化趋势大致相似，都是开始下降平缓，然后快速下降，然后又趋于平缓。总体来说，na越大，平均总成本越大。图7为4种可再利用比例下，随着na变大，平均总成本先上升，到达峰值后下降，之后又再上升。总体来说，ma越大，平均总成本越小。

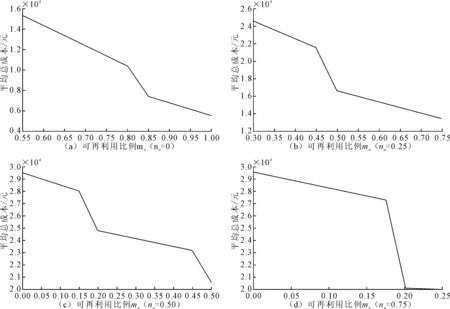
图6 平均总成本随ma的变化

图7 平均总成本随na的变化

取不同可再利用比例ma和再生电池可回收比例na下20组数据，进行方差分析，结果如表2所示。由F分布表可查F0.05(3,12)=3.49，F0.05(4,12)=3.26。因为Fma=15.71>3.49，所以废弃回收中可再利用比例ma对平均总成本有显著影响；因为Fna=2.28<3.26，所以再生电池的可回收比例na对平均总成本没有显著影响。

表2 ma和na方差分析表

3 总结

(1)根据PULL策略，以市场对电池需求为主导因素，针对废旧铅蓄电池回收企业设计了库存模型，并通过算例验证了模型的可行性，为铅蓄电池回收处理的库存控制提出了一种可行方案。

(2)废旧电池的再生过程中制造速率逐渐增大时，平均总成本先快速下降，超过一定速率后下降趋于平缓，再提高制造速率(产能)对降低平均总成本效果不明显；电池拆解速率对平均总成本影响有限。

(3)对废弃回收电池的两种比例进行显著性分析，发现可再利用比例ma是影响平均总成本的关键因素，再生电池的可回收比例na对平均总成本影响不显著。