基于WOA优化卷积神经网络的齿轮箱故障诊断研究

刘 奇，唐红涛，高晟博，李 冰

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.武汉理工大学 数字制造湖北省重点实验室，湖北 武汉 430070)

齿轮具有传动比大、体积小、承载能力大等优点，同时作为减速箱的关键零件，由于其长期处于恶劣的工况条件下，也是设备最易损坏的部分。此外，齿轮一旦出现不同程度的失效，整个减速箱乃至整台设备都可能出现故障，这些故障引起的设备重大问题屡见不鲜。

为了维持设备的安全运行，避免造成不必要的停机维修损失，需要对齿轮进行状态监测和故障诊断，这也成为国内外众多学者的研究对象。例如，雷亚国等[1]从动力学建模和动态信号处理两方面分析了行星齿轮箱故障诊断的国内外研究进展，指出当前研究中存在的关键问题并讨论了解决这些关键问题的方法和途径； Hinton等[2]通过“逐层预训练”来有效克服深层神经网络在训练上的困难，从而掀起了深度学习的浪潮。近年来，越来越多的学者开始尝试将卷积神经网络(convolutional neural network，CNN)应用于工业设备的故障诊断中,虽然卷积神经网络的层数、池化方式、激活函数、分类器等结构参数可依据经验进行选择，不需要优化，但是卷积核的个数、大小、学习率等参数并没有明确的选取规则，显然随机选择容易使神经网络陷入局部最优。

综上所述，笔者结合鲸鱼算法(whale optimization algorithm)，其具有结构简单、参数少、搜索能力强且易于实现等特点，提出了WOA-CNN诊断模型，利用WOA对卷积神经网络参数进行优化，避免模型陷入局部最优解。

1 卷积神经网络

卷积神经网络[3]结构一般包括输入层、卷积层、池化层、全连接层和输出层5部分，笔者主要研究两个卷积层和两个池化层的CNN网络。

1.1 卷积层

卷积过程是用多个卷积核对输入图像进行卷积运算，然后将输出加上偏置后，通过激活函数进行非线性变换，对于二维图像信号，卷积定义为：

(1)

1.2 池化层

池化操作[4]是图像的下采样过程，主要作用是对卷积层输出特征进行压缩，以减少特征图。池化方式有最大值池化、均值池化、高斯池化和可训练池化。针对齿轮周期性振动的时域信号，为了获取与位置无关的特征，采用最大值池化方式。池化操作运算公式为：

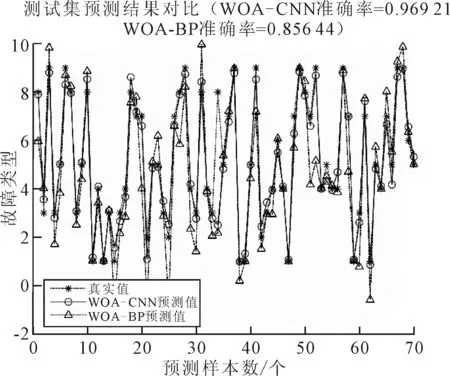
hn=max(jn-1)W

(2)

式中:hn为第n池化层池化结果；jn为第n层第j个池化切片；W为池化区域；fn为第n卷积层卷积结果。

2 基于WOA优化CNN的算法设计

鲸鱼优化算法[5](WOA)是一种模拟座头鲸捕猎的群智能优化算法，其结构简单、收敛速度快且易于实现。算法分为包围猎物、泡泡网攻击和搜索猎物[6]3个步骤，因此，用系数矢量A来区别是环绕包围猎物还是随机搜索行为。

为了提高模型的收敛速度和准确率，笔者设计了一种基于WOA优化CNN结构参数的算法(WOA-CNN)，采用WOA对两个卷积层卷积核的数量k1、k2，大小s1、s2，训练批次batch，学习率η进行优化[7]，将上述6个参数映射成每头鲸鱼个体的空间向量位置，第n头鲸鱼的位置为：

xn=(k1n,k2n,s1n,s2n,batchn,ηn)

(3)

(1)包围猎物。鲸群在捕食猎物过程中，对于猎物的位置是未知的，基于动态变换的猎物位置。WOA算法假定目标最佳位置就是鲸鱼最接近猎物时的位置，并包围它。为此，引入系数向量A，当|A|小于1时，选择鲸鱼种群中最接近目标的鲸鱼个体作为局部最优猎物xgbest，此时CNN得到的适应度值最小，其余个体向着这个位置逐渐包围猎物，位置更新公式为：

D=|C·xgbest(t)-xn(t)|

(4)

xn(t+1)=xn(t)-A·D

(5)

式中:t为当前迭代次数；·为逐元素相乘并非向量运算中的点乘；A和C的更新公式为：

A=2a·r1-a

(6)

C=2·r2

(7)

式中:r1、r2是[0,1]中的随机向量；a为收敛因子，其变化公式可设置为：

(8)

式中:N为最大迭代次数。

(2)泡泡网攻击。鲸鱼在捕食过程中，一方面连续吐出气泡形成一种圆柱形气泡网，将猎物包围起来，采用收缩包围机制；另一方面会作螺旋姿势旋转上升，向水面游动，采用螺旋更新位置机制[8]。假设鲸群选择收缩包围和螺旋更新两种情况的几率各占50%，则鲸鱼位置的更新公式分别为：

xn(t+1)=xgbest(t)-A·

|C·xgbest(t)-xn(t)|p<0.5

(9)

xn(t+1)=D′·ebl·cos(2πl)+

xgbest(t)p≥0.5

(10)

式中:D′=|xgbest(t)-xn(t)|表示第n头鲸鱼到最佳位置的距离；b为螺旋线常数；l为[-1,1]中的随机数。

(3)搜索猎物。鲸鱼可以根据彼此的位置进行随机搜索，当|A|≥1时，在鲸群中随机选择一头鲸鱼xrand(t)作为局部最优位置，并以此更新其他鲸鱼的位置。更换公式为：

xn(t+1)=xrand(t)-A·|C·xrand(t)-xn(t)|

(11)

在WOA算法中，每头鲸鱼要朝着猎物的位置移动，鲸群之间更新猎物信息，猎物最终的位置也就是鲸群中位置最优的个体，此时将猎物的位置作为CNN网络结构的全局最优参数，对应最佳适应度值。WOA-CNN算法流程如图1所示。 鲸群捕食行为具体步骤为：

图1 WOA-CNN算法流程图

(1)信号预处理。由于上述6个物理量有不同的单位和量级，在训练神经网络前需要对采集到的数据进行归一化处理。此外，还需要将一维时域信号转化成二维“矩阵”，“矩阵”中每一个像素点代表信号值。

(2)数据集划分。将训练集、测试集组数按3∶1划分，并且保证训练集中各故障类别下的数目相等，用以验证WOA-CNN模型训练和测试结果的准确度。

(3)鲸群初始化。鲸群种群初始化参数只有鲸鱼种群个数n和迭代次数N，设置n=20，N=70。初始化种群后，种群中的每头鲸的位置都是用一个6维向量表示适应度评价指标。常用公式包括：平均绝对误差、均方误差等，笔者采用交叉熵函数检验回归损失。

(4)捕食行为。捕食行为具体步骤为：

Step1每头鲸位置更新。当p≥0.5时，鲸群根据式(10)更新个体位置；当p<0.5且|A|<1时，鲸群根据式(4)更新个体位置；当p<0.5且|A|≥1时，鲸群根据式(11)更新个体位置。

Step2计算更新后鲸鱼的适应度值。将更新后每头鲸鱼的6维向量作为CNN的结构参数，用训练集训练后用测试集测试，计算均方误差值，记录每个个体的适应度值和当前迭代时间，并筛选出与当前一代中的最佳适应度值相对应的鲸鱼位置。如果更新的局部最优值比上一代的局部最优鲸鱼更好，则用xgbest(t+1)取代全局最优鲸鱼xbest；反之用全局最优鲸鱼xbest取代局部最优鲸鱼，并重新更新所有鲸鱼的位置，再计算适应度值。

Step3结束条件。判断迭代次数是否满足t>N，如果不满足，则返回Step1重新迭代计算，否则结束局部深度搜索。

(5)故障分类。由于每条鲸鱼xi=(k1i,k2i,s1i,s2i,batchi,ηi)的空间位置不同，即每次训练CNN的结构参数都会发生变化，针对不同的CNN网络结构参数，用相同的训练集和测试集来训练和测试，其中训练集是已知故障类别标签的，测试集是标签未知的。CNN的输出层采用Softmax函数将输出信号转化为概率和为1的分布，计算第i次迭代的平均损失值。最终，鲸群经过N次迭代寻优操作后，找到平均损失值最小的那一代，对应的即为全局最优鲸鱼，也就是猎物位置。

(6)模型重构。得到全局最优鲸鱼xn=(k1n,k2n,s1n,s2n,batchn,ηn)的位置后，将最优的卷积核数量、大小、训练批次、学习率等6个参数重构CNN模型，并采用训练集训练，测试集测试，此时CNN模型故障分类准确率最高。

3 实验结果对比分析

3.1 数据说明

为了验证WOA-CNN模型在齿轮箱故障诊断中的可行性，采用PHM协会比赛使用的齿轮箱数据PHM 2009 Challenge Data[9]。被诊断的齿轮共有3种故障：齿轮破裂、断齿、过度磨损，每种类型的故障均对应3种齿数的齿轮：输入齿轮/32齿、第一惰轮/96齿、输出齿轮/80齿。因此，将故障类型设置为10种，并在公开数据集中每种类型故障分别取120 000个样本，将120 000个样本分成300组数据，将训练集和测试集按3∶1比例分配，10种故障累计3 000组数据。将上述数据作为卷积神经网络的输入时，由于每组数据都是1×400的一维矩阵，为了提高卷积速度，特将一维矩阵转化成20×20的二维图像。

3.2 实验结果

为了验证WOA-CNN模型的分类准确率，构建WOA-BP(whale optimization algorithm-back propagation)、CNN、PSO-CNN(particle swarm optimization-convolutional neural network)、WOA-CNN 4种模型用来对比分析各类模型用于故障诊断时的优缺点。为了突出各模型的分类准确率，这里直接给出每种模型经过算法迭代后得到的最优神经网络参数，并利用这些优化后的参数重构网络模型。

(1)WOA-BP故障诊断模型。采用鲸鱼优化算法对BP神经网络的隐含层神经元个数、步长、训练精度、学习率进行优化(假定该神经网络只有1个隐含层)，即每头鲸鱼个体由一个4维向量xi=(ni,batchi,gi，ηi)组成，采用交叉熵函数作为损失函数。得到优化后的BP神经网络的隐含层神经元个数为139，步长为41，训练精度1e-3，学习率为0.041 725。

(2)CNN故障诊断模型。如果卷积神经网络结构参数没有进行优化，容易陷入局部最优解，可能导致过拟合现象。因此该模型采用前述提到的CNN结构参数，即两个卷积层卷积核的数量k1=16，k2=8；大小s1=9×9，s2=5×5；训练批次batch=100；学习率η=0.009，采用交叉熵函数作为损失函数。

(3)PSO-CNN故障诊断模型。粒子群算法(PSO)具有结构简单、收敛速度快等特点，种群初始化参数为：惯性权重w=0.9；加速度因子c1=c2=2；初始粒子个数为20；迭代次数为200。由前述分析可知，初始种群中，每个粒子个体也由一个6维向量xi=(k1i,k2i,s1i,s2i,batchi,ηi)组成，用式(12)、式(13)更新粒子的位置和速度，直至找到全局最优粒子的位置。

(12)

(13)

优化后的PSO-CNN结构参数为：两个卷积核的数量k1=16，k2=30；大小s1=8×8，s2=4×4；训练批次batch=84；学习率η=1.063 7e-5。

(4)WOA-CNN故障诊断模型。由前所述，鲸群初始化种群个数n=20；迭代次数N=70。通过WOA算法优化CNN后得到的结构参数为(16，30，3×3，3×3，50，9.3697e-4)。将上述4种模型优化后得到的参数重构神经网络，然后用训练集对上述4个模型进行训练，并通过测试集进行测试，统计5次分类精度和时间消耗取平均值，如表1所示。

表1 4种模型5次运算平均值对比

由表1可知，BP神经网络结构较为简单，优化后的CNN较之于未优化的深度学习神经网络具有更高的识别准确率，但是由于模型更为复杂，运算时间也大大增加。为了说明WOA-CNN模型良好的表征性能，用T分布随机近邻嵌入算法[10](t-SNE)对高维数据进行降维处理，将特征聚类输出，获得二维分布结果，如图2所示。

图2 降维处理后的特征聚类输出的二维分布结果

图2分别表示不同迭代次数中训练样本分类情况，说明WOA-CNN模型在公开数据集中的分类效果较好。将10种故障类型下的加速度信号分别采集300组作为训练集，另取70组样本作为测试集，并且根据振动信号时域频域波形图提取加速度有效值、峰值、能量因数、峰峰值、频幅值、稳定超调量、包络解调值7种特征。将WOA-BP和WOA-CNN模型进行对比，测试结果如图3所示。

图3 WOA-BP模型与WOA-CNN模型对比结果

根据10次测试结果的统计，WOA-CNN模型的平均分类精度约为98.46%，而WOA-BP模型的平均分类精度约为91.71%，表明WOA-CNN模型对齿轮箱故障具有良好的分类效果，也说明卷积神经网络在齿轮故障诊断方面有较好的准确率。

4 结论

笔者基于CNN强大的图像识别能力，针对其网络结构参数难以确定的问题，利用鲸鱼算法优化CNN网络结构，得到最优的卷积核大小、个数、学习率等参数，构造最优的故障模式识别分类器。通过实验结果可以看出，针对齿轮箱公开数据集，WOA-CNN模型相比于其他算法均能够在较少的迭代次数下达到较好的分类识别效果。