基于页岩气多重运移机制的二项式视渗透率公式

袁迎中，严文德，戚志林，李继强，黄小亮

(1.复杂油气田勘探开发重庆市重点实验室重庆科技学院，重庆 401331； 2.重庆科技学院，重庆 401331)

0 引 言

页岩气作为一种重要的非常规天然气资源，由于其分布广泛、储量巨大，开发技术极具挑战性，近年来受到人们的持续关注。与常规气藏不同，页岩气藏具有黏性流、滑脱流、Knudsen扩散和表面扩散等不同的气体运移机制[1-3]。在一定压差下，页岩气的流量可用达西方程的形式表示，视渗透率可以描述页岩气在孔隙介质中的运移能力[4-5]，孔径分布、孔隙类型和连通性、应力状态、非均质性和吸附性对页岩气的视渗透率均有重要影响[6-7]。

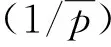
页岩气在微纳米孔隙运移过程中，气体分子之间相互碰撞，又与孔壁碰撞。碰撞后气体分子的速度存在一定程度的损失，造成分子运移受阻。同时，吸附气体分子会沿孔壁表面运移，使分子的运移能力提高。准确预测页岩气运移能力及视渗透率的变化规律，对于分析页岩气藏开发动态十分重要。基于页岩气的多重运移机制，建立了基质视渗透率与平均压力倒数的二项式公式。该公式考虑了速度梯度随孔壁距离的变化，同时也考虑了与压力倒数的平方有关的表面扩散视渗透率，描述了页岩气视渗透率随压力降低而增加的非线性变化趋势，可有效地解释现有的视渗透率测试数据，计算表面扩散引起的视渗透率和表面扩散系数，为研究页岩气的多重运移机制奠定了理论基础。

1 考虑滑脱效应的二项式视渗透率方程

Klinkenberg[8]提出了考虑气体滑脱效应的视渗透率公式：

(1)

(2)

(3)

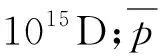
式(1)认为孔壁附近的速度梯度为常数。如果考虑孔壁附近速度梯度的变化，且孔壁附近的速度满足二阶泰勒级数公式，则视渗透率为[10]：

(4)

定义线性项与非线性项分别为：

(5)

(6)

由此得到：

(7)

(8)

(9)

式中：Kapp1为黏性流、滑脱流及速度损失引起的视渗透率，m2；K1a为黏性流、滑脱流引起的视渗透率，m2；K1b为因速度损失而减少的视渗透率，m2。

式(9)中，文献[10]推导出b1=4m2/r2，经仔细研读原文并重新推导公式，应为b1=2m2/r2。

2 考虑滑脱效应和Knudsen扩散的二项式视渗透率方程

黏性流和滑脱流由气体分子间碰撞而产生，Knudsen扩散由气体分子与孔壁的碰撞而产生。Knudsen扩散引起的视渗透率可以表示为[1]：

(10)

式中：Kd为Knudsen扩散视渗透率，m2。

定义比例系数：

(11)

(12)

(13)

(14)

综合考虑黏性流、滑脱流和Knudsen扩散及各自的比例系数，则总视渗透率的线性项可以表示为：

K2a=w1K1a+w2Kd

(15)

将式(5)、(10)代入式(15)，得：

(16)

(17)

式中：w1为黏性流和滑脱流占总传输量的比例系数；w2为Knudsen扩散占总传输量的比例系数；Kn为Knudsen数；λ为气体分子的平均自由程，m；K2a为考虑不同传输比例的黏性流、滑脱流及Knudsen扩散引起的视渗透率，1015D。

计算结果表明，K1a与K2a基本相等，即方程(5)能够反映Knudsen扩散对视渗透率的影响。

考虑非线性项，视渗透率Kapp2为：

(18)

式中：Kapp2为黏性流、滑脱流、Knudsen扩散及速度损失引起的视渗透率，1015D。

3 考虑滑脱效应、Knudsen扩散和表面扩散的二项式视渗透率方程

表面扩散为吸附在页岩孔隙表面的气体分子在吸附势场作用下沿孔隙表面运移的现象。由表面扩散引起的视渗透率可以表示为[1]：

(19)

式中：Ks为表面扩散视渗透率，1015mD；Ds为表面扩散系数，m2/s；Cs为吸附气质量浓度，kg/m3。

(20)

(21)

(22)

综合考虑黏性流、滑脱流、Knudsen扩散和表面扩散，总视渗透率Kapp可以表示为：

Kapp=Kapp2+Ks

(23)

将式(18)、(22)代入式(23)，得

(24)

(25)

式(24)中，a1和b1之间的关系难以确定。由于K1a≈K2a，则有：

(26)

式(24)可以改写为：

(27)

式(27)比式(24)更便于分析实验数据。如果考虑实际气体的偏差因子，则上述公式中的“RT”应替换为“ZRT”。

4 实例分析

4.1 二项式视渗透率理论曲线分析

计算页岩气视渗透率的基本参数如下：孔隙度φ为0.05，气体黏度μ为0.02 mPa·s，气体常数R为8.314 J·(mol·K)-1，温度T为343 K，气体摩尔质量M为0.016 kg/mol。

利用式(27)计算的视渗透率曲线，如图1所示。由图1可知：不同孔隙半径及不同c值的视渗透率与压力倒数呈非线性关系，曲线曲率为负，随着压力倒数的增加，视渗透率的增加先是近线性的，而后增加的幅度越来越低；曲线的形状受r和c的影响，c值越大，气体分子与孔壁的碰撞越强烈，分子的速度损失和二项式曲线的曲率越大；c值相同时，随着r的增大，Knudsen扩散和滑脱效应减小，二项式曲线的曲率减小；当r达到25 nm时，视渗透率曲线近似直线。

图1 不同c值时视渗透率与压力倒数的理论曲线Fig.1 The theoretical curves of apparent permeability and pressure reciprocal value at different values of c

4.2 实验数据分析

根据Moghadam & Chalaturnyk的实验数据[10](图2)，回归的视渗透率公式为：

图2 不同压力倒数时视渗透率实验测试数据[10]Fig.2 The experimental test data of apparent permeability at different pressure reciprocal values[10]

(28)

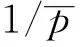
根据式(24)，表面扩散引起的参数bs的值为9.483 7-1.897 2= 7.586 5。图2所示的平均压力为2.778 7 MPa， 由此计算得到Ks为0.001 051 mD。平均压力下总视渗透率为0.004 161 mD，其中，表面扩散视渗透率占25.26%。

理论上，b值与表面扩散能力有关。如果b的实际值远小于理论值，则认为表面扩散在页岩气运移中起着重要作用；如果b的实际值接近理论值，则表面扩散不是页岩气的重要运移机制；在某些情况下，b的实际值可能大于理论值，说明页岩气储层的孔径较大，气体分子与孔壁碰撞引起的动量损失不明显。

5 结 论

(1) 基于黏性流、滑脱流、Knudsen扩散和表面扩散等页岩气多重运移机制，考虑了速度梯度随孔壁距离的变化，建立了基质视渗透率与平均压力倒数的二项式公式，描述了页岩气视渗透率随平均压力倒数的增加而非线性增大的变化趋势。

(2) 基质视渗透率与平均压力倒数之间的曲线形状受孔隙半径r和参数c的影响，c值越大，气体分子与孔壁之间的碰撞越强烈，二项式曲线的曲率越大。对于相同的c值，随着孔径r的增大，Knudsen扩散和滑脱效应减小，二项式曲线的曲率减小。

(3) 文中方法能有效地解释已有的视渗透率实验数据，平均压力下表面扩散引起的视渗透率为0.001 051 mD，占总视渗透率的比例为25.26%。