基于多次数据吸收集合平滑算法的自动油藏历史拟合研究
王泽龙,刘先贵,唐海发,吕志凯,刘群明
(1.中国科学院大学,北京 100049;2.中国科学院大学渗流流体力学研究所, 河北 廊坊 065007; 3.中国石油国际勘探开发有限公司,北京 100034;4.中国石油勘探开发研究院,北京 100083)
0 引 言
油藏数值模拟技术是室内油藏工程研究的重要手段。传统油藏数值模拟技术是将油藏地质模型与流体模拟程序相结合,再输入流体性质参数和生产制度,经过大量计算从而得到预测数据。地质模型静态参数主要包括渗透率、孔隙度、初始温度、压力等,动态数据来自现场油井的实测生产数据。但研究过程中要求具备较高的地质学和油藏工程专业素养,才能较好地完成地质模型的调整工作。在实际工作中,如果油田处于开发初期,或者从业人员经验尚浅,人为手动修正的地质模型往往不能够真实反映出油藏地质特征[1]。此外,现代油藏管理需要进行不确定性分析,纯粹的人工历史拟合已难以适应发展要求。
自动油藏历史拟合技术自20世纪90年代进入快速发展阶段,大量学者开展了相关研究[2-5]。GeirEvensen通过改进卡尔曼滤波线性问题的局限,提出了扩展卡尔曼滤波,后为克服其敏感性矩阵的大量计算问题,提出集合卡尔曼滤波[6],即EnKF,并开始在天气预测领域应用。Nævda等[7]将EnKF引用到石油工程领域,用于更新油井附近的油藏模型,Lorentzen[8]、Oilver[9]、Chen[10]、Reynolds[11]、Jafarpour[12]、王玉斗[13]、薛亮[14]等学者均在EnKF引入到油藏模拟应用领域进行了大量研究,但均未彻底解决EnKF算法在油藏历史拟合中计算效率低,且更新后的状态参数与实际的状态参数不一致的问题。Reynolds[15]发现对相同实测数据的多次数据吸收可以改善EnKF的效果,Emerick与Reynolds[16]结合集合平滑算法,提出了多次数据吸收集合平滑算法,即ES-MDA。在前人研究成果基础上,进一步推导出ES-MDA算法的核心公式,开发了自动历史拟合软件,确定了多次数据吸收的选择参数,并应用于海相砂岩油藏的历史拟合,取得了较好的应用效果。
1 数据吸收算法的数学描述
EnKF和ES都是利用状态参数(如孔隙度、渗透率、压力、饱和度等)的集合,近似表达先验概率的期望值和方差,通过求解后验概率的期望值,实现后验概率期望值与真值的误差最小化、后验概率方差最小化的计算过程。在此基础上,通过求得的后验概率,得到更新后的状态参数,从而获得更新后的油藏模型。2种算法均属于蒙特卡洛模拟的范畴,基于贝叶斯概率论来计算后验概率。
不同点在于:EnKF是在整个时间序列中一步一步地吸收实际测量数据,逐步更新后验概率估计;ES则是却在整个时间、空间域中,一次性吸收所有实测数据,直接更新整个油藏模型的后验概率估计。对于线性问题,ES简单高效。但对于非线性和混沌动态系统,EnKF相对于ES要更加优越,状态集合的迭代更新过程符合实测数据所代表的真实情况。以下简要对EnKF与ES算法进行数学描述。
1.1 EnKF与ES算法的数学描述
1.1.1 EnKF算法
EnKF是目前油藏历史拟合中应用最广泛的数据吸收算法。定义扩展状态向量xk为时间序列k时刻估算的状态参数,包括地质模型的静态参数、油藏的主要动态参数以及实测数据。
(1)
式中:m为地质模型的静态参数向量在k时刻的估值;p为动态参数向量(如油藏压力、油气水饱和度等);d为实测数据向量(如油气产量、产水量、井底压力等);下标k为时间步;x为扩展状态向量。
EnKF的预测方程为:
(2)
(3)

EnKF的更新方程为:
(4)
H=[OI]
(5)

为方便计算,定义卡尔曼系数矩阵K为:
(6)
则,EnKF的更新方程可表达为:
(7)
同理,在k+1时刻及未来任意时刻,可通过连续循环以上过程,不断更新地质模型集合。EnKF算法需要实时输入状态参数,同步进行正向的模拟计算,因此,EnKF更新方程中,模型参数和状态参数同时更新,会造成更新后的状态参数与实际的状态参数不一致。如油藏的状态压力、温度以及流体饱和度等参数的更新,与后验地质模型的模拟结果相互矛盾。
1.1.2 ES算法的数学描述
ES可以全局性吸收所有时间序列的实测数据,并一步完成后验概率的计算。对于一套静态地质模型,只需运行一次完整时间序列的油藏流体模拟即可完成。因此,可直接由静态地质参数矩阵mk代替扩展状态参数矩阵xk,预测方程可表示为:
(8)
(9)
ES算法的更新方程为:
(10)

ES算法能够一次性批量完成数据吸收并一次性完成所有模型集合的更新,避免了EnKF算法中需要频繁调用正演模型文件获得状态参数的缺点,但由于油藏模拟是一个非常复杂的非线性计算过程,ES算法的更新不能给出准确预测结果,故不能应用于油藏历史拟合。
1.2 ES-MDA算法的数学描述
借鉴EnKF算法多次循环迭代的思路,减小ES算法单次更新的步长,在小步长的情况下,对油藏模拟进行线性处理,通过多次小步长的更新完成计算,即为ES-MDA算法。
首先,人为选择数据吸收的次数Na,并且针对每次数据的吸收过程定义系数αi,满足如下关系:
(11)
在每次数据吸收过程中,进行以下步骤操作。
(1) 运行整套静态地质模型集合的油藏模拟程序,获得全时段的预测数据。
(2) 对于集合中任意一个模型子集,按照式(12)为实测数据添加误差。
(12)
式中:dobs为实测数据。由于测量数据存在误差,为修正误差引入白色噪音向量zd,zd符合高斯分布zd~N(0,I)。
(3) 得到ES-MDA更新方程。
(13)
ES-MDA算法的流程框图见图1。
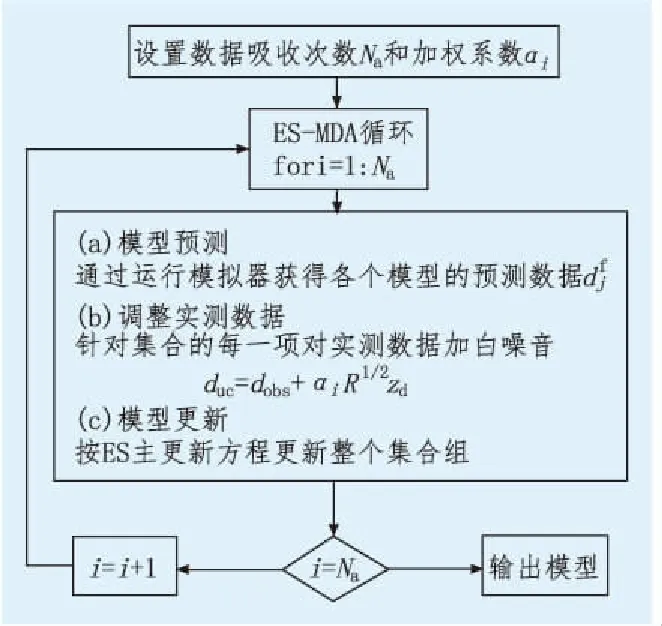
图1 ES-MDA算法的流程框图Fig.1 The flow chart of ES-MDA algorithm
相比EnKF,ES-MDA按照平滑算法的方式,一次性完成对所有历史数据的吸收,进而减少了油藏状态参数的代入需要,避免了油藏状态参数更新异常问题。同时,ES-MDA是基于卡尔曼滤波在线性问题上构建贝叶斯概率理论似然函数的算法,其直接适用条件是线性问题或近似线性问题,并且参数的概率分布为高斯分布,初始模型的参数集合足够大。大量文献[10-13,17]证明EnKF作为集合算法的一种典型,当地质模型参数集合足够大(如100组)时,即可取得较好的历史拟合效果,故可推断ES-MDA算法适应于油气藏历史拟合。按照上述方法,通过Matlab编程形成了一套自动历史拟合程序,可用于油藏历史拟合的实例研究。
2 实例应用
2.1 油藏地质及开发概况
北海布伦特油田总体为西东向带状半圆顶背斜构造,构造面积为31.5 km2,内部发育一条近东西走向断层,北部边界为闭合断层。主力油藏埋深为1 956~2 210 m,油水界面在背斜顶部以下90 m处,油藏厚度约为15 m,初始含油饱和度约为80%,油藏类型为无气顶边底水油藏。沉积物源方向为近西东向,储层岩相为砂岩,伴随少量泥岩夹层,具有较强的非均质性。储层孔隙度为5.1%~34.2%,平均为18.5%;储层水平方向平均渗透率为325 mD,垂直方向平均渗透率为26 mD,为常规高孔高渗储层。地层压力系数为1.11,属正常压力系统。原始地层压力为18 MPa,地层温度为76 ℃。地面原油密度为0.71 g/cm3,76 ℃原油黏度为0.31 mPa·s。
本研究中,对照组给予常规用药治疗,观察组则给予常规用药联合无创呼吸机治疗。结果显示,观察组COPD并呼吸衰竭治疗效果高于对照组,P<0.05;观察组呼吸衰竭纠正的时间、住院时间优于对照组,P<0.05;治疗前两组PCO2、PO2两项血气指标和心率相近,P>0.05;治疗后观察组PCO2、PO2两项血气指标和心率优于对照组,P<0.05。
该油藏于2008年开始投入开发,以四点法部署开发井网,平均井距为1 000 m,部署油井20口、注水井10口,均为直井,所有井均配备数据传感器,用于实时收集井口动态生产数据。截至目前,区块累计产油1 165×104m3,采出程度约为32%。
2.2 ES-MDA自动油藏历史拟合
2.2.1 模型建立
油藏构造模型由74×24×7个正交立方网格组成,网格大小为150.0 m×150.0 m×4.5 m。鉴于储层岩相主要为海相砂岩,且孔隙度、渗透率呈高斯分布,采用序贯高斯模拟(简称SGSim)进行随机储层建模。以井口测井解释孔隙度及钻井取心测量渗透率作为随机储层建模硬数据约束,结合储层沉积成藏认识,选取以下参数进行SGSim建模:水平方向最长相关长度为5 000 m,方位角为80°W,其正交方向相关长度为500 m。为定量描述储层参数的置信度,通过SGSim生成100个初始地质模型集合。以渗透率为例表述静态地质参数的更新调整,图2a为100个初始地质模型的渗透率平均值分布,图2b为其中4个初始地质模型子集的渗透率分布。由图2可知,100个初始地质模型展现出100种油藏的非均质情况,但在渗透率平均值模型中,每个网格的数值都接近地质模型中渗透率的数学期望值,且变化趋势光滑,因此,仅以井口采样点数据作为约束条件的建模结果置信度较低。在初始的油藏认识情况下,一般用100个初始地质模型集合的平均值作为制订开发方案的依据。按照闭合油藏管理理念,在获得足够油田开发动态数据后,进行油藏历史拟合,对初始地质模型进行修正,以获得更准确的更新地质模型。
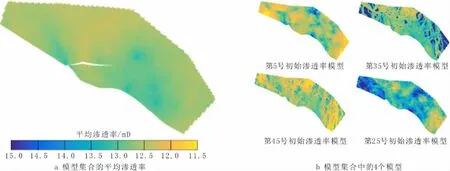
图2 初始地质模型集合的渗透率模型Fig.2 The permeability model of the initial geological model ensemble
2.2.2 历史拟合
利用该地质模型及自主编写的ES-MDA油藏自动历史拟合程序对油田内20口油井、10口注水井进行历史拟合,程序输入文件为井口生产动态数据以及100个等概率油藏初始模型构成的集合。设置ES-MDA数据吸收次数为4,每次数据吸收的系数分别为α1=α2=α3=α4=4。每次数据吸收对单个油藏模型均调用一次油藏模拟器,并按照油田生产制度进行油藏全时段数值模拟,共进行400次油藏数值模拟运算,耗时2 d。自动历史拟合程序输出结果分别为更新后的地质模型集合以及动态数据拟合图表,拟合结果(图3~7)较好,各项预测指标与完测数据的误差均控制在10%以内,较好地反映了油藏实际。
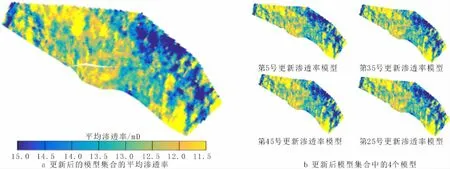
图3 更新地质模型集合的渗透率模型Fig.3 The permeability model of the updated geological model ensemble
图4~6为实测与模型预测的生产参数对比,由图4~6可知:原始模型的预测数据具有很大的分散性,主要原因是地质参数的不确定性;而经过历史拟合后的更新模型预测数据集中程度很高,且基本与实测数据吻合,再次证明更新地质模型的置信度很高。

图4 生产井原油产量拟合结果
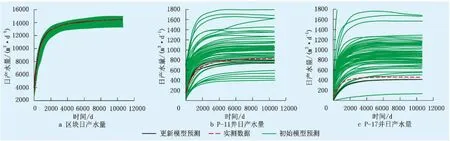
图5 生产井产水量拟合结果Fig.5 The matching results of water yield of production well
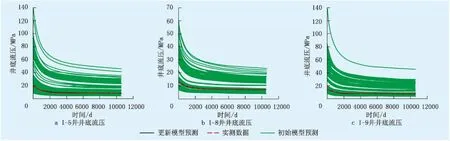
图6 注水井井底压力拟合结果Fig.6 The matching results of downhole pressure of water injection well
为定量分析历史拟合的置信度,定义油藏流体数值模拟的预测相对误差为e,用于评判拟合后的模拟数据与实际测量数据的偏离程度。计算方法为:
(14)
式中:N为模拟数据的个数。
通过ES-MDA算法更新地质模型,地质模型集合中各项地质参数接近,模拟结果具有很高的集中度(表1~3),油井的产油量以及注水井的井底流压拟合结果较好,误差在1%左右;油井的产水量拟合结果稍差,但误差也低于10%。

表1 北海布伦特油田某区块产油量历史拟合统计Table 1 The history matching statistics of oil yield in a block of the Brent Oilfield in the North Sea

表2 北海布伦特油田某区块产水量历史拟合统计Table 2 The history matching statistics of water yield in a block of Brent Oilfield in the North Sea

表3 北海布伦特油田某区块井底流压历史拟合统计Table 3 The history matching statistics of downhole flowing pressure of a block of the Brent Oilfield in the North Sea
在效率方面,自动历史拟合优势明显,大尺度油藏模拟,若采用人工历史拟合需要数月时间,而应用ES-MDA油藏自动历史拟合,相同条件下效率可提高数百倍。与EnKF算法相比,ES-MDA算法效率也可提高5倍以上。
3 结 论
(1) 对于线性问题,ES算法能够一次吸收所有时间序列数据,模型一次更新到位;但对于非线性问题,比如复杂油藏的模拟过程,由于ES算法计算步长过大,存在模型修正失真的问题。
(2) 通过有效结合ES算法和EnKF算法,推导出ES-MDA算法的核心公式,形成了自动油藏历史拟合软件。在实际应用中,地质模型集合中各个子项参数均需呈高斯分布,否则需要对模型参数进行高斯化处理。
(3) 应用ES-MDA算法对北海布伦特油田进行自动历史拟合,结果表明更新后地质模型集合的子集模型之间渗透率分布具有更高的一致性,能够有效表征真实油藏地质特征,且通过其开展的油藏数值模拟达到预期效果,预测数据与实测数据匹配程度达到90%以上。

