对一道阿基米德三角形作业题的研究性学习
李 宁
(海南省海南中学 571158)
一、问题再现
在2020年“停课不停学”期间,笔者通过网络平台给学生布置的作业中有这样一道题目:
抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为“阿基米德三角形”.阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上.设抛物线y2=2px(p>0),弦AB过焦点,△ABQ为阿基米德三角形,则△ABQ的面积的最小值为( ).

二、从通性通法角度解答
学生未必都能了解阿基米德三角形的性质,比如参考答案直接说∠Q为直角,就显得莫名其妙.可以着眼于求三角形面积最值的通性通法去思考.

与抛物线方程联立,得y2-2y0y-p2=0.
设A(x1,y1),B(x2,y2),则y1+y2=2y0,y1y2=-p2.


解法2 (根据陈英昊、姚正宇等同学的解答整理)

与抛物线方程联立,得y2-2pmy-p2=0.
设A(x1,y1),B(x2,y2),则y1+y2=2pm,y1y2=-p2.


三、研究性质用性质
对于抛物线y2=2px(p>0),弦AB过焦点F,弦AB中点为M,此时的△ABQ为阿基米德焦点三角形.下面研究相关性质.
性质1 阿基米德焦点三角形的顶点Q在抛物线的准线上.
性质2 阿基米德焦点三角形底边AB上的中线与抛物线的对称轴平行或重合.
由性质2可以把解法2后半部分做一点改进:
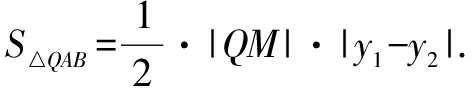


性质3 在阿基米德焦点三角形QAB中,QA⊥QB,QF⊥AB.
由性质1和性质3,可以从几何上思考这道作业题.


图1
解法4 (根据潘逸声同学的解答整理)过点A,B分别向准线引垂线,垂足为点D,E.由点B向AD引垂线,垂足为点C,准线与x轴交点为点G.
在Rt△ADQ和Rt△AFQ中,AQ为公共斜边,|AD|=|AF|,从而|DQ|=|QF|.
同理,|EQ|=|QF|.

点评如果熟悉性质,解决这道作业题还是挺轻松的,如解法3.但是如果是解答题,还是需要严格论证,掌握通性通法.
四、相关练习
练习1 已知抛物线C:y2=4x,圆M:(x-a)2+(y-2)2=4,若圆M上总存在点P,使得过点P的抛物线C的两条切线相互垂直,则实数a的取值范围是____.
练习2 已知抛物线C:x2=4y,点M是C的准线l上的动点,过点M作C的两条切线,切点分别为P,Q,若O为坐标原点,则O到直线PQ的距离的最大值为____.
练习3 过抛物线C:y2=2px(p>0)的焦点F作直线l交抛物线于A,B两点,抛物线在A,B两点的切线交于点Q.若|AB|=8p,则S△QAB=____.
参考答案:1.[-3,1](轨迹思想,切线相互垂直则切线交点在准线上,只需⊙M与抛物线准线有公共点即可);
2.1(定点意识,直线PQ过焦点);

