赏析几道“Dandelin双球”模型的圆锥曲线问题
陈凌燕 蔡海涛
(1.福建省厦门市海沧中学 361022;2.福建省莆田第二中学 351131)
蔡海涛(1975-),男,福建省莆田人,本科,中学高级教师,从事高中数学教学研究.
数学家Germinal Dandelin证明“平面截圆锥得到的截口曲线是圆锥曲线”的方法非常巧妙,在圆锥内放两个大小不同的球,使得它们分别与圆锥的侧面、截面相切,通过纯几何的方法证明截口曲线是圆锥曲线,该模型称为“Dandelin双球”模型.本文赏析几道“Dandelin双球”模型的圆锥曲线问题,期与同行交流.
例1仿照“Dandelin双球”模型,人们借助圆柱内的两个内切球完美地证明了平面截圆柱的截面为椭圆面.如图1,底面半径为1的圆柱内两个内切球球心距离为4,现用与两球都相切的平面截圆柱所得到的截面边缘线是一椭圆,则该椭圆的离心率为( ).

部析结合已知条件,画出轴截面图,如图2,易知圆柱的底面直径为椭圆的短轴长,即2b=2.
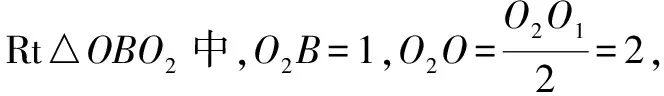

为什么“与两球都相切的平面截圆柱所得到的截面边缘线是一椭圆?”
证明如图3,设平面与球O1,球O2分别相切于A,B两点,设边缘线上点P,过点P作与圆柱母线平行的直线切球O1,球O2于M,N两点,则由切线长相等,有PA=PM,PB=PN,所以PA+PB=PM+PN=MN=O1O2.所以点P的轨迹是椭圆,A,B是其两焦点.
例2 如图4,两个底面半径为3,高为4的圆锥内分别有1个半径为1的小球与圆锥侧面相切,平面π与两个小球都相切,且截圆锥所得的边缘线为双曲线,则该双曲线的离心率为____.
剖析设两个小球与平面π分别切于点F1,F2,与圆锥两部分分别截得圆S1,S2,任取边缘线上一点P,连接OP分别交圆S1,S2于点Q1,Q2,则|PF1-PF2|=|PQ1-PQ2|=|Q1Q2|,所以点P轨迹是以F1,F2为焦点的双曲线.


例3 将篮球放在地面上,被阳光斜照留下的影子的边线是椭圆,如图6.如果将光源换成点光源,则影子的边线可能是( ).
A.椭圆 B.双曲线的一支 C. 抛物线 D. 圆
剖析阳光斜照篮球留下的影子的边线可以看作是平面被圆柱截得的边缘线,所以是椭圆.阳光换成点光源,可以看作是平面被圆锥截得的边缘线,则椭圆,双曲线的一支,抛物线,圆都有可能.当点位于球正上方,可以看作是与圆锥旋转轴垂直的平面截圆锥,所得边缘线为圆.当点位于与平面距离等于球直径的位置时,可以看作是与圆锥母线平行的平面截圆锥,所得边缘线为抛物线,如图7所示.

推广与圆锥母线平行的平面截圆锥所得的截口曲线是抛物线.
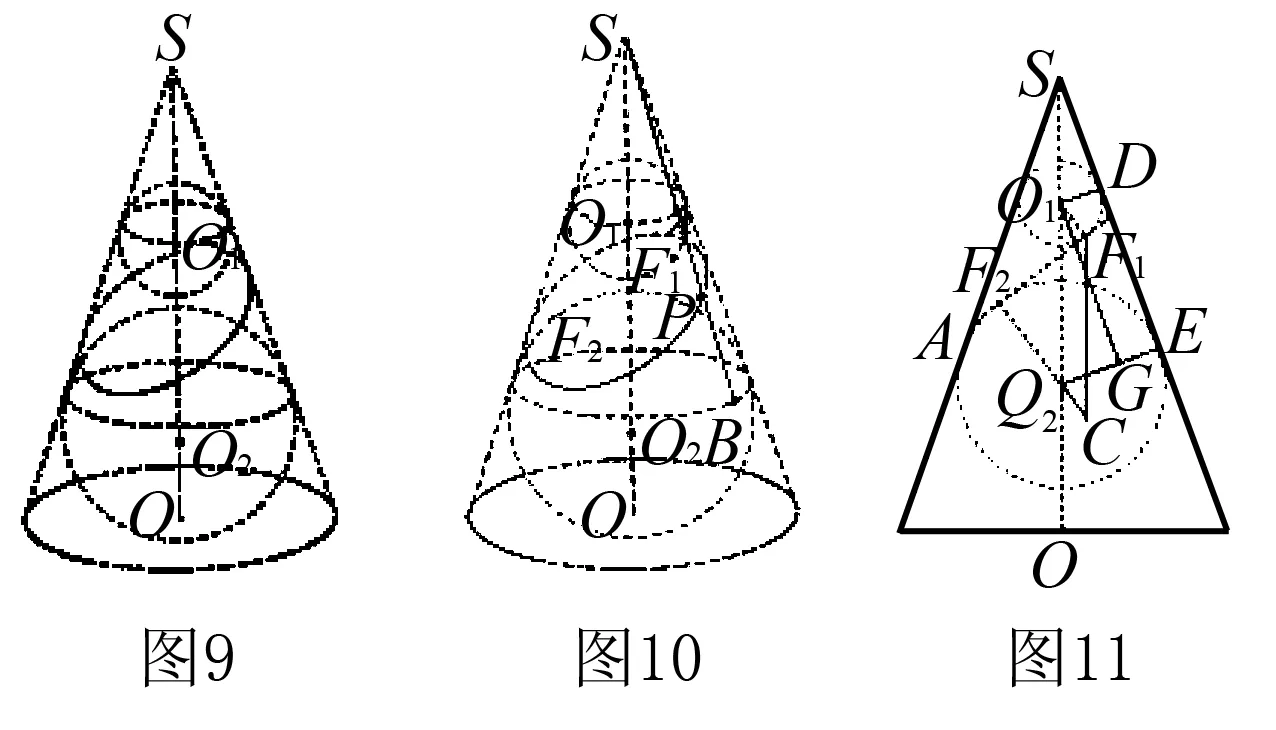
设圆锥母线与圆锥旋转轴所成角为θ,如图8,设小球O与圆锥相切的⊙O1所在平面为α,与圆锥母线平行的平面β与平面α相交于直线l,平面β与小球O相切点F,设点P为截口曲线上任一点,连接PS交⊙O1于点B,设点P在平面α的投影为P0,连接BP,过点P0作P0A⊥l交l于点A,连接PA,由三垂线定理,知PA⊥l,所以∠PAP0为二面角α-l-β的平面角,所以∠P0PA=θ.又∠BPP0=∠SPP0=θ,所以Rt△BPP0≌Rt△APP0,所以PB=PA.又由切线长相等,知PF=PB,所以PF=PA,所以点P的轨迹是抛物线,焦点是F,准线是l.

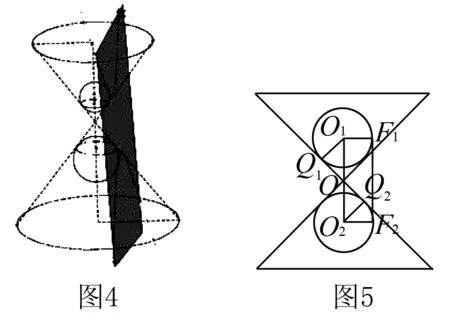
剖析如图10,设球O1,O2与圆锥SO相切于圆S1,S2,与平面α相切于点F1,F2,任取截口曲线上一点P,直线SP与圆S1,S2相交于点A,B,由切线长相等,知PF1=PA,PF2=PB,所以PF1+PF2=PA+PB=AB,所以点P的轨迹是以F1,F2为焦点的椭圆.设椭圆长轴长为2a,焦距为2c.
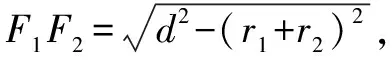



根据椭圆的第二定义:到定点的距离与到定直线的距离之比为小于1的常数.定直线就是椭圆的准线,即小球与圆锥相切的圆所在平面与椭圆所在平面的交线就是椭圆的准线.
由上例分析,“Dandelin双球”模型的圆锥曲线问题只需借助模型分析,掌握“平面截圆锥得到的截口曲线是圆锥曲线”的几种模型,问题的解决就不难了.

