分动器输出轴齿轮热装配技术的实践
田晋跃
(江苏大学汽车与交通工程学院,镇江 212013)
齿轮热装配方法可以减小齿轮和与之连接轴的加工要素,降低生产成本,提高齿轮的装配精度。如果处理得当,热装配的齿轮传递的扭矩、传动比、转速也可以达到花键连接的水准。
本文结合大速比分动器设计,在输出轴齿轮采用热装配技术,根据零部件材料的性质,确定过盈量和装配间隙,分析热装配接触压力、齿轮与轴之间的摩擦力等特性,最后采用KISSSOFT软件进行产品校核和安全性计算。
1 结构参数
热装配过程是将预热后的齿轮装配在外径大于该齿轮内孔直径的轴上,齿轮和轴的配合采用过盈配合,装配前将齿轮加热,齿轮受热膨胀,内径增大、轮毂伸长,装配时轮毂的一个端面贴住轴的基准端面,在环境温度下,齿轮温度下降,产生径向和轴向的收缩,内孔缩紧套在轴颈上,完成齿轮的热装配。
图1为输出轴热装配齿轮结构示意图(图中用I标出)。该分动器输出转矩为12 000 N·m,输出轴最高转速为2 000 r/min,速比分别为1.00和6.03,实现车辆的前后桥驱动。齿轮和轴的材料均采用20CrMnTi,表面渗碳深度0.7 mm~1.0 mm,表面硬度HRC58-64。

图1 输出轴热装配齿轮结构示意图
图2为热装配的公差控制示意图。图中D为公称直径,B为装配长度,δ为热装配的控制公差。

图2 热装配的公差控制示意图
2 齿轮与轴过盈量计算
齿轮与轴过大的盈量会产生一定的装配应力,生成结合面的静摩擦,保证传递转矩的要求。图3为所建立的齿轮与轴过盈配合的理论计算模型。由于热装过程中,齿轮受热套装在轴上,冷却后,只有沿圆周均布的接触压力qa。
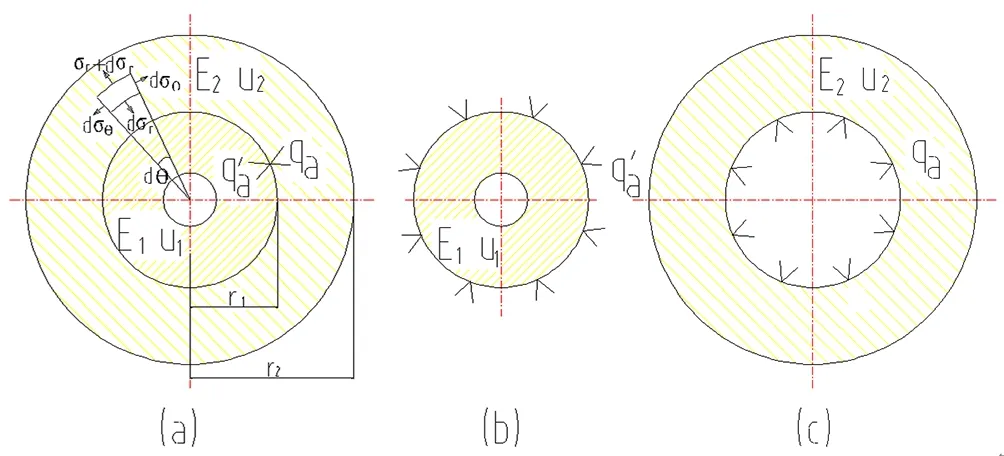
图3 轴与齿轮过盈配合理论计算模型
根据工程力学理论,平面微元力的平衡有:
(1)
式中:σr—径向应力;σθ—环向应力;r—径向半径。
微元应变的几何及物理关系有:
(2)
式中:εr—径向应变;εθ—环向应变;E—弹性模量;μ—泊松比;u—所取微元径向的位移。
可得周向应力和环向应力:
(3)
对式(3)求导,并代入式(1)有:
(4)
对式(4)积分,并代入边界条件,对于轴有:
(5)
负号代表尺寸减小。
对于齿轮有:
(6)
齿轮装配在装配结合面处的公差为:

(7)
3 齿轮热收缩的过程
齿轮装配前,进行预热,温度至t℃,齿轮内孔直径D受热膨胀了ΔD。论文没有考虑齿轮宽度B增大ΔB的影响。
ΔD=αD(t-t0)
(8)
式中:ΔD—齿轮内孔直径受热膨胀增量;α—材料热膨胀系数;D—齿轮内孔直径;t0—装配环境温度。
将加热后的齿轮取出,压装至轴上。齿轮温度从t下降,齿轮冷却收缩,收缩开始阶段,齿轮内径收缩量小于装配间隙e时,收缩不受其他影响,称为自由收缩;齿轮内孔直径收缩至轴直径时,齿轮与轴开始接触,此时收缩受到轴的影响,称为约束收缩。即ΔD=δ+e,其中e为装配间隙。
齿轮进入约束收缩阶段时,齿轮与轴开始接触,齿轮继续收缩,压迫轴反作用力压迫齿轮内孔表面,齿轮内孔表面压力为qa。
4 分动器齿轮与轴热装的公差确定
齿轮和轴的材料均采用20CrMnTi,弹性模量E=E1=E2=207 GPa,泊松比μ=μ1=μ2=0.25,材料屈服应力[σ]=425 MPa。设定齿轮的装配温度为180 ℃ ~200 ℃之间。
考虑齿轮传动工作时,需要传递转矩,在装配结合面具有剪切应力τrθ存在,即τrθ=βqa,其中静摩擦系数β=0.15。同样在在装配结合面处,σr=-qa,σθ=((r22+r12)/(r22-r12)qa。根据强度理论:
(9)
计算得σθ、σr值代入式(9),并根据第3强度理论,有:
σ3rd=σ1-σ3=2.582qa
根据σ3rd<[σ]/n,安全系数n=1.5。得:σ3rd<283.33 MPa。即可以得到:qa<109.72 MPa。由qa值,代入公式(7),得:δ>0.042 1 mm。通过确定的σ值,选定配合尺寸参数见表1。

表1 分动器输出轴齿轮与轴的尺寸参数
5 分动器齿轮与轴热装的性能参数及安全系数
根据所选的输出轴齿轮与轴的尺寸参数及材料,采用KISSSOFT的软件进行装配安全性校核,得到装配安全系数见表2,同时获得相关计算的结果如表3。
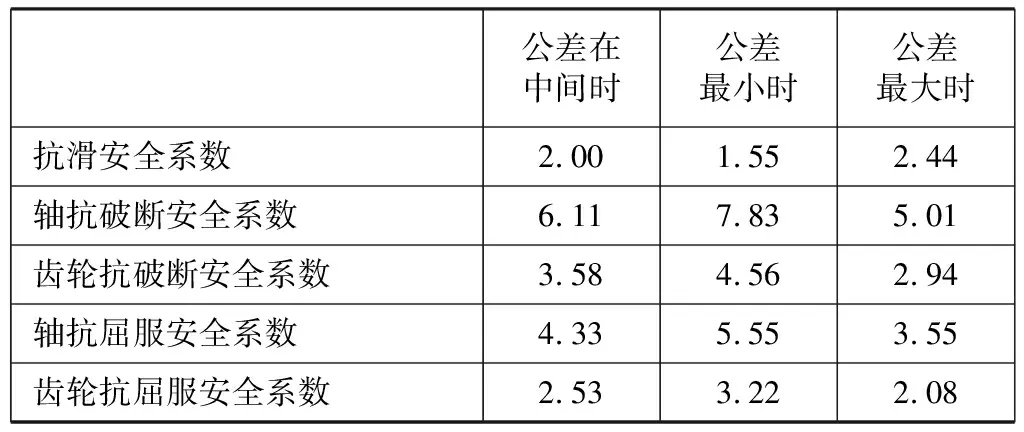
表2 装配相关安全系数计算值

表3 KISSSOFT计算结果
考虑齿轮热装配后的齿形误差会发生变化,分析检测了齿形的三个参数值,见表4。检测结果表明,热装后齿轮的齿距积累公差、齿廓积累公差和齿向积累公差是有变化的,但变化值在设计要求范围内。

表4 齿形误差的检测结果
该分动器经过3年多的试验和装车使用,输出齿轮与轴的热装配安全可靠。图4为分动箱的安装使用图。

图4 齿轮热装输出轴的分动箱的应用
6 结论
齿轮与轴热装是一个复杂的工艺过程,可以减小齿轮和与之连接轴的加工要素,提高齿轮的装配精度。本文根据分动箱输出轴和齿轮的材料性质,提出过盈量和装配间隙的计算方法,可以满足齿轮与轴之间的力学特性和接触应力要求,各项安全系数也满足工程应用需要。

