基于混合模型ad ap tive L ASSO方法的气象数据实时变点检测*

黄雄琪，田镇滔，秦 睿，王雪梅，郑陈亮

（广西师范大学 数学与统计学院，广西 桂林 541004）

1 研究意义及其背景

近年来，全球气候变暖备受国内外学术界的关注。全球气候的变化在近几年的数据报告中呈现出致灾性的特点，例如高温、强风、强降雨这些极端天气会促使自然灾害的发生，继而严重影响各国人民的生命财产安全。气候变化所导致的一系列影响，让全世界的学者们不得不重视气象数据变点的分析及预测。

国内外有不少学者在研究变点问题。对于响应变量的个数比较少的情况，Horváth.L等[1]通过最小二乘的方法使用CUSUM方法检测出了变点。Ga⁃briela[2]通过使用adaptive LASSO以及分位数的方法检测出实时的变点。杨喜寿等[3]研究了气候时间序列变点的推断问题。Hawkins[4]研究了位置转移替代方案的似然比检验，并应用于气象数据序列的变点检测。Buishand[5]讨论了5种累积偏差检验的特点，使用累计偏差与平均值构建了检验统计量，并对荷兰年平均气温进行了变点检测。Alexandersson.H[6]等基于气候时间序列，提出了一种在正态分布时间序列中检测任意长度序列变点的新方法。Beaulieu.C[7]等考虑了气候时间变化的复杂性和气候数据序列的自相关性，提出了一种基于IA(informational ap⁃proach)的变点检测模型。赵红等[8]基于VFP环境，对气象数据使用滑动t-检验法和Yamamoto法进行变点的检测。许欢9]等运用ASAMC算法估计了气象数据结构性变化的位置并给出了发生结构性变化的原因。

本文将降雨量作为被解释变量Yi，将风向、风级等作为解释变量X1,…,Xp，并且还考虑了被解释变量的滞后性，引入变量Yi-1,…,Yi-k。通过Lasso方法找到了这几个变量之间的关系，并且找出了降雨量对应的解释变量的参数发生突变的时间点(变点)。

2 建立混合回归模型

首先考虑简单线性模型：

接下来结合解释变量的滞后性，考虑如下模型：

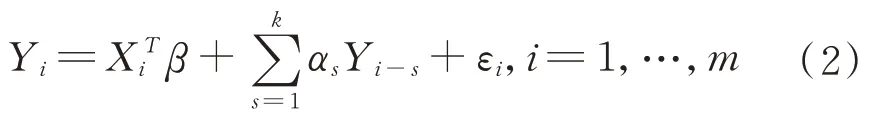
我们可以把(2)式转化成如下模型：

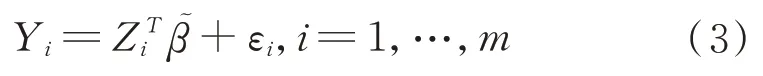
通过前m个观测值得到简单的最小二乘估计：

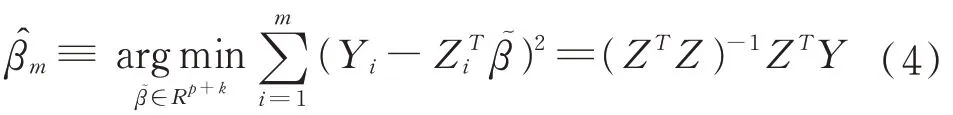
通过BIC准则可以筛选一些变量，但是筛选出来的变量不精确，借助LASSO可以解决变量的稀疏性问题，这个方法是1996年由Tibshirani.R提出的。在设计矩阵Z满足某些且不使用假设检验的情况下，来消除掉一些不相关变量。之后在2006年zou提出了一种叫作的adaptive LASSO的方法，这个方法不需要设计矩阵Z的那些条件，方法如下：

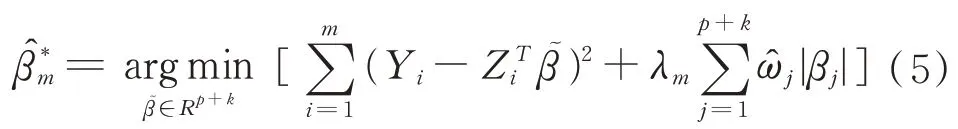
由此我们可以得到相应估计的残差：

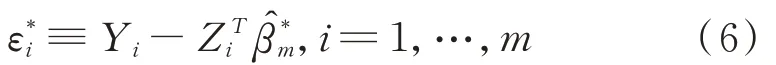
为了便于表述，引入指标集A≡{j∈{1,…,p+k};≠0}，同 理A*m≡{j∈{1,…,p+k};≠0}。其中A是真实参数的非零分量的指标组成的集合，A*m是使用adaptive LASSO估计得到参数的分量指标组成的集合。一般地对于参数͂，我们用表示包含A相关因子的͂的子向量。

考虑如下假设：

对于误差εi：

（S1）ε1,…,εm,εm+1,…是独立同分布的，E[ε1]=0，方差有限Var(ε1)＜∞，

（S2）对于解释变量X1,…,X p,Y i-1,…,Y i-k存在一个正定矩阵C和常数η＞0，有，更进一步要求εi与Z i是独立的。

在条件（S1）下Card(A)不依赖于m，设计矩阵m-1Z T Z收敛到一个正定矩阵C，调节参数λm有如下条件

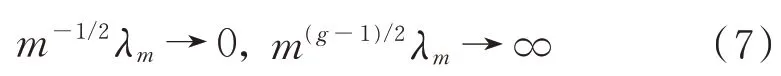
有adaptive LASSO估计值满足oracle性质：

（P1）渐近正态性：

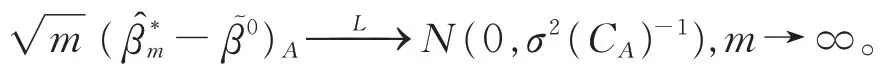
矩阵CA包含矩阵C对应的指标集A中的元素，对于β的最小二乘估计，可以得到

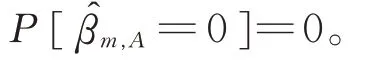
用上述方法得到β的估计后，我们可以得到总体方差σ2的估计：

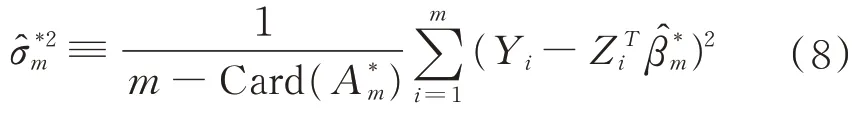
其中，Card(A*m)表示A*m的基数。

由于Card(A)不依赖于m，考虑adaptive LAS⁃SO的估计值的oracle性质，可以得到

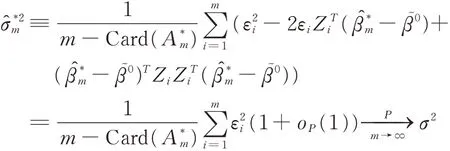
3 利用CUSUM方法构造检验统计量

首先考虑第一批m个观测值之后的模型：

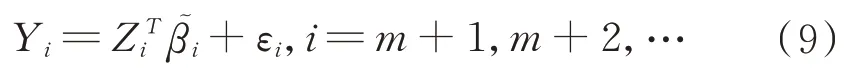
对于每一个给定的时间i，检验该模型的参数是否和第一批m个模型的参数一致:

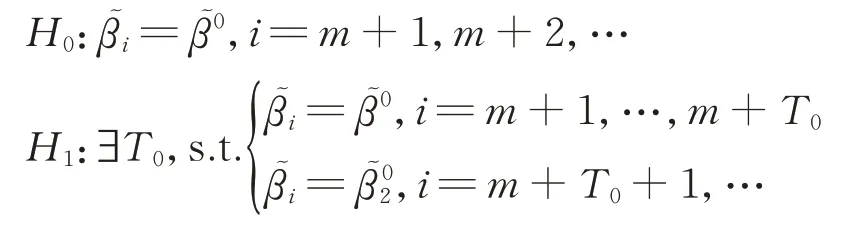
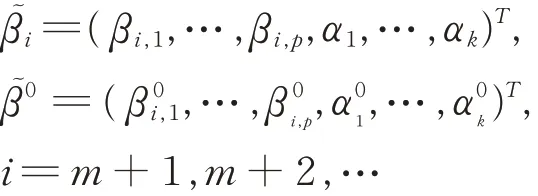
假设模型（2）是显著的，即

为了构造统计量，将采用Horváth.L等的CU⁃SUM（cumulative sum）方法，在此之前先求出=Y i-,i=m+1,…,m+T，然 后 求的CU⁃SUM，即：对于某个T＞0,

对于给定常数γ∈[0,1/2)，考虑归一化函数（此归一化函数为有界函数）：

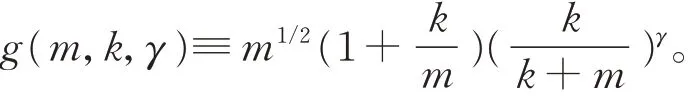
引理1在满足假设（S1）（S2）的条件下，

（2）当备择假设成立时，有

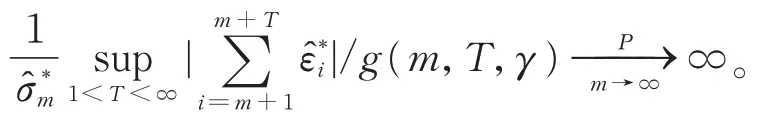
因此，根据上述假设检验可得到相应的检验统计量

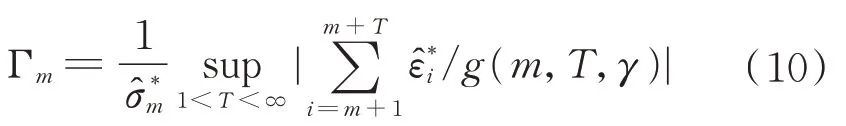
引理2对于给定的显著性水平α容易通过模拟计算得到对应的分位点cα(γ)，因此，当原假设被拒绝时，可以得到停时：

4 桂林市降雨数据的变点估计

基于第二章提出的变点检测模型，对广西桂林市的降雨量真实数据进行实证分析。

气象数据的预测问题是气象学研究领域中公认的较为复杂的课题之一，其中降雨量为气象数据预测中最难课题之一，降雨量大小引发的地质灾害关系着人民生命财产安全，因此对降雨量大小的监控和精准预测是一项非常重要的工作。本文选取广西桂林市的真实降雨量数据，基于第二章提出的变点检测模型对降雨量的时间序列数据进行检测分析，得出影响降雨量的因素以及降雨量的变点时刻，进而为相关气象部门做好防护预警提供有力的依据，已达到减少人民生命财产损失的目的。

本章数据来自广西桂林市2019年1月1日至2019年12月31日的降雨量情况。其中影响桂林市降雨量的变量如表1所示。

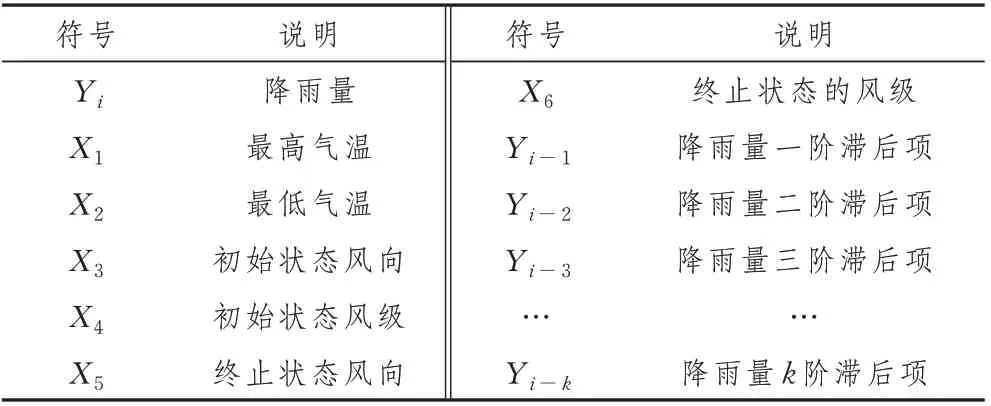
表1 桂林市降雨量的变量

图1是桂林市降雨量情况的周度数据图，可以看出时间在第23周时，降雨量发生骤变，容易看出这个数据是存在变点的，因此可以对桂林市降雨量数据进行变点检测。

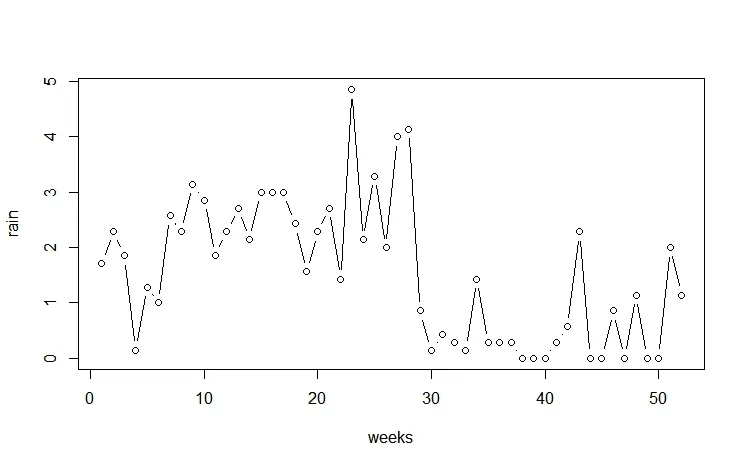
图1 桂林市降雨量时序图（周度数据）

首先研究降雨量数据的滞后情况。对数据进行时间序列分析，确定该降雨量序列是2阶滞后的，因此确定滞后项阶数k=2。

其次选用较简单的最小二乘法(4)对降雨量数据进行分析，得到该模型(3)的最小二乘法估计为=(5.89,-0.34,0.06,0.025,-0.04,0,0,-0.21)T。

然后选用adaptive LASSO方法(5)对降雨量数据进行分析，得到该模型(3)的adaptive LASSO估计为=(4.66,-0.26,0,0,0,0,0,-0.06)T，再 根 据 得到adaptive LASSO估计易得总体标准差估计(8)为=0.73。

接下来根据数据模拟得到统计量的分位数为(γ=1 4,α=0.05)和cα(γ)=42.37645，并根据计算不同时间点统计量的值可以得到停时=83。

最后综合上述分析和结果得出，只有最高气温和降雨量一阶滞后项两个解释变量是影响广西桂林市降雨量情况的因素，并得到桂林市2019年1月1日至2019年12月31日降雨量的变点在第m个数据后的第83个位置，按照实际时间计算得到变点时刻为2019年4月13日。换句话说，在4月中旬来临之前，相关部门应该提前做好防洪防汛工作，防止内涝和次生灾害的发生。桂林市在2017年和2020年分别发生了内涝，导致了政府和人民财产的损失。使用该方法对降雨量进行分析，可以为当地部门提供有效有力的数据支持和决策意见，以防止人员伤亡及财产损失。

2019年4月13日正值桂林市湿润季风影响下的雨季，也是当地人俗称的“南风天”。这说明本文建立的基于混合回归模型adaptive LASSO方法较为准确的将实时降雨量骤变点检测出来了，解决了一个气象数据难预测的问题，进而得出该模型检测效果不错，能够较为准确的定位降雨量变点，并且结果符合实际情况，具有较大的实际意义，也为后续研究其他气象问题提供一种好用又准确的方法。