气囊隔振器耐压强度研究

成玉强，帅长庚，徐国敏

（1.海军工程大学振动与噪声研究所，武汉 430033；2.船舶振动噪声重点实验室，武汉 430033）

0 引 言

气囊隔振器是一种具有非线性静、动态刚度的减振元件，它可利用空气压缩的非线性刚度和阻尼特性来隔离振动和冲击,已经被广泛应用在车辆和舰船减振降噪领域[1-2]。气囊隔振器的囊体一般由帘线骨架层和内外橡胶层组成，其中，帘线骨架层是囊体的主要受力载体，由能够承受极大拉力的高强度纤维和橡胶硫化形成[3-4]。在设计气囊隔振器时，为保证气囊的可靠性，往往需要对囊体的帘线骨架层进行失效分析，以确保气囊满足耐压强度要求。

现有气囊耐压强度的理论模型中一般仅针对某一型气囊进行耐压强度分析，且仅将帘线的破坏作为气囊隔振器失效的判断标准[5-6]。由于囊体的帘线骨架层是由帘线与橡胶硫化形成的各向异性材料，其失效形式并不能单独由帘线决定，而应考虑帘线增强复合材料的整体力学性能。因此，现有理论模型往往并不准确。

气囊一般可分为囊式、膜式和复合式三种结构，其中囊式和膜式两种结构应用较多，复合式结构由于结构复杂，应用较少[7-8]。本文将囊式和膜式结构气囊简化为旋转壳结构，建立统一力学模型，结合帘线复合材料模型的力学分析，推导出囊体耐压强度表达式，能准确地计算气囊的耐压强度，并对囊体的帘线缠绕角度进行了优化设计，为气囊隔振器的可靠性设计提供理论指导。

1 建立模型

气囊隔振器主要由上盖板、囊体、下盖板和约束法兰等部件组成，如图1（a）所示。图中P为囊内气压，F为气囊隔振器承载力，α和β分别为上下约束法兰的导向角度，Re为气囊隔振器的有效半径。

旋转面是由一平面曲线与此曲面共线的一轴旋转而成，此曲线即为经线，其平面为经线面。现将气囊隔振器囊体简化为旋转面形壳，如图1 所示，用二相邻经线和二平行圆截取壳的一单元体，经线的位置由从某一基准经线面量起的角度θ决定，平行圆的位置由壳面的垂线和旋转轴所夹角度φ决定。经线面和垂直于经线的平面是旋转面某一点的主曲率面，其相应的曲率半径分别用ρ和R0表示。

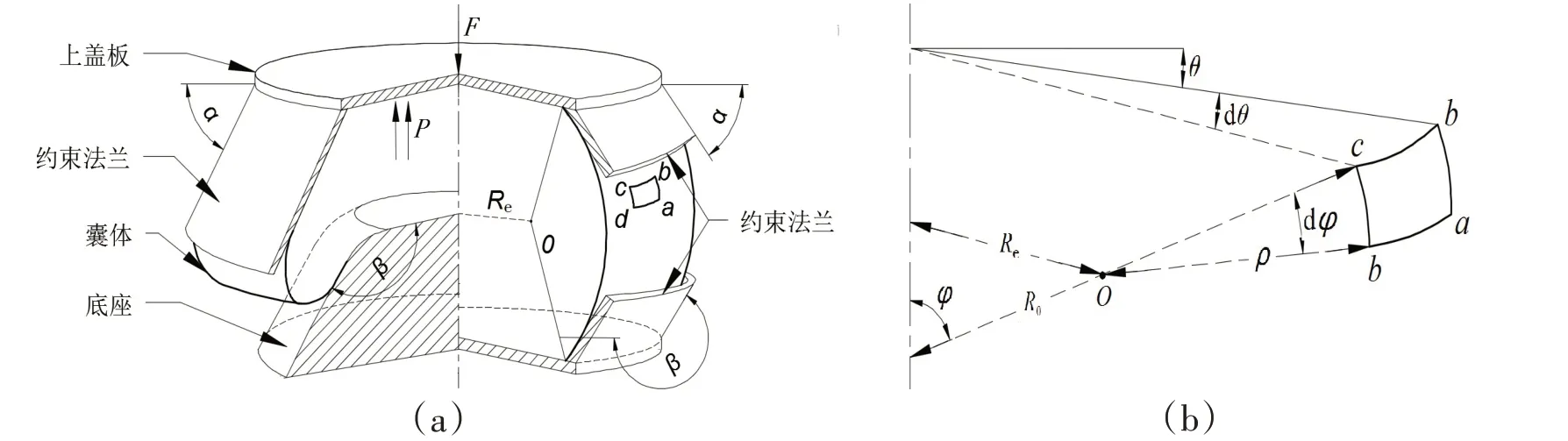
图1 气囊隔振器结构参数示意图Fig.1 Schematic diagram of air spring

图1中，φ的取值范围为[α,2π -β]，假定φmax为某型气囊隔振器φ的最大值，则当0 ≤φmax≤π时，此为囊式结构气囊，如图1（a）右侧结构所示；当π ＜φmax≤2π时，此为膜式结构气囊，如图1（a）左侧结构所示。由几何结构模型可得ρ、R0和Re之间的函数关系为

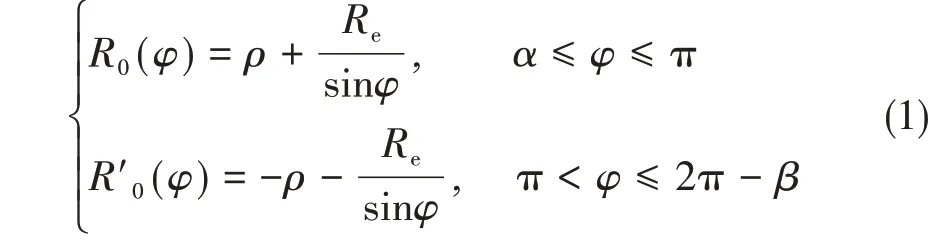
如图2 所示，对微元进行受力分析，Nφ和Nθ分别为囊体经线和纬线方向上单位长度截面上的内力，因气囊隔振器囊体厚度远小于另外两个方向上的尺寸，并且受到剪切力和弯矩易变形，因此可根据薄壳无距理论进行分析。分析过程中假设条件如下:

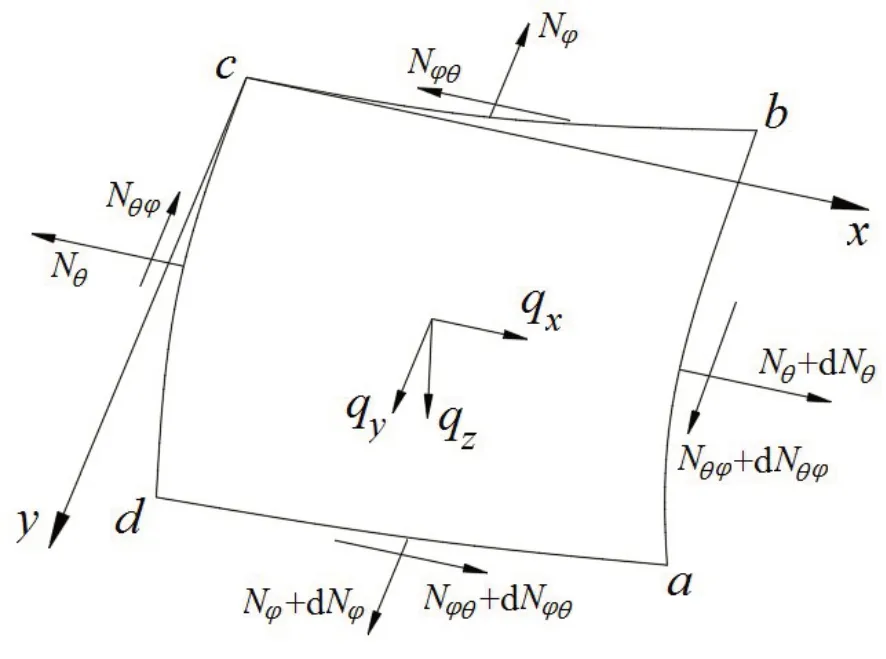
图2 囊体微元受力分析图Fig.2 Capsule micro-element force analysis

（1）金属套筒相对于囊体变形很小，故将金属套筒视为刚体，同时分析过程中不考虑与金属套筒接触的囊体部分；

（2）因图1中力学模型的外载荷对于中心轴对称分布，即无qx分量，故薄膜剪力Nφθ和Nθφ为零，仅存在薄膜内力Nφ和Nθ，通过囊体平衡性分析可建立Nφ和Nθ的函数表达式为[9]

由式（2）推导过程中的约束条件可得，该式仅适用于承受轴对称载荷且可以忽略剪切力和弯矩的理论模型，而针对受到偏心力以及剪切力与弯矩不能忽略的情况，该式并不适用。

2 模型求解

2.1 求解内力表达式

如图3 所示，将壳体沿平行圆切开，然后将微小长度上Nφ的竖直分量Nφsinφ相加，令其与截出壳体上的外力总垂直分量之和为0。现假定Nφ的正方向为由外向内沿着卷曲囊体的经线方向，Nθ的正方向为绕中心轴的顺时针方向。结合式（2）即可解得Nφ和Nθ的表达式为

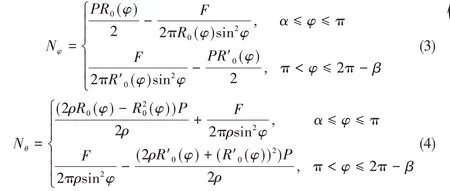
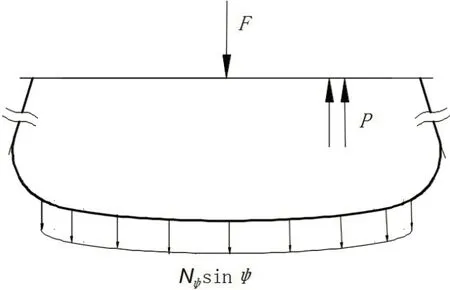
图3 气囊内力平衡分析Fig.3 Air spring internal forcebalance analysis

对于囊式和膜式气囊隔振器，其承载特性方程皆可表示为[10-11]

将式（1）和式（5）代入式（3）和式（4）中，即可得到囊体内力表达式为

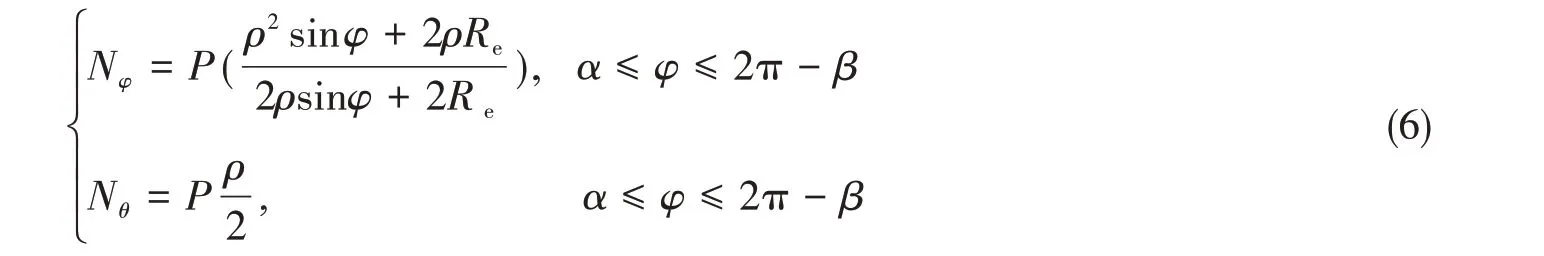
2.2 求解囊体耐压强度表达式

假设σφ和σθ分别为囊体经向应力和纬向应力，t为帘线骨架层的厚度，则由式（6）可得σφ和σθ参数表达式为

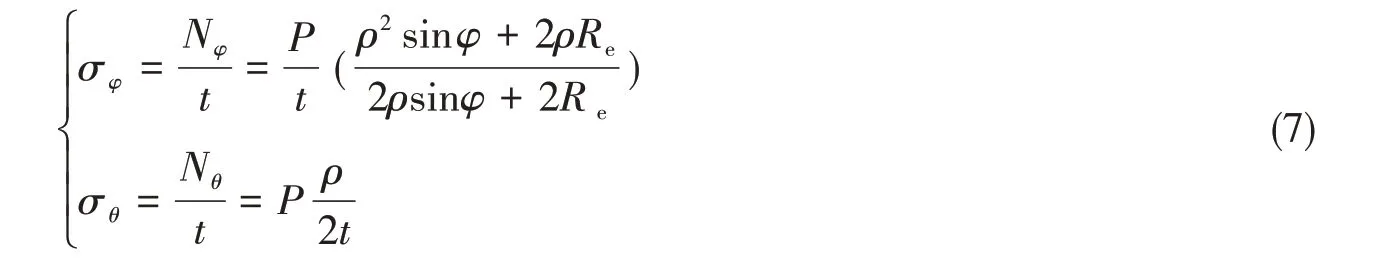
建立骨架层复合材料微元模型，如图4 所示。图中，σx为σφ和σθ的合应力；ω'为力学平衡角，为合应力方向与囊体纬向方向的夹角；σ1，σ2和σ12分别为复合材料微元模型的轴向、横向以及剪切主应力；e和f分别为微元模型的纬向和经向长度；g为微元模型在以主应力方向为法向方向的平面上的投影长度。可得到ω'和σx的表达式为

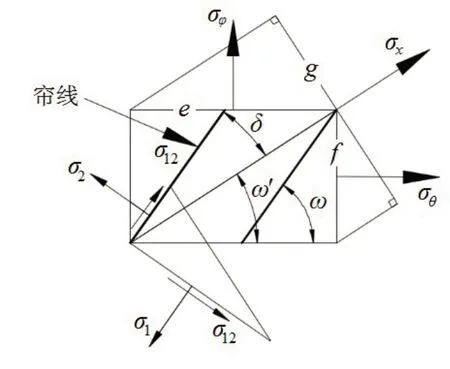
图4 骨架层复合材料微元模型Fig.4 Skeleton layer composite material microelement model

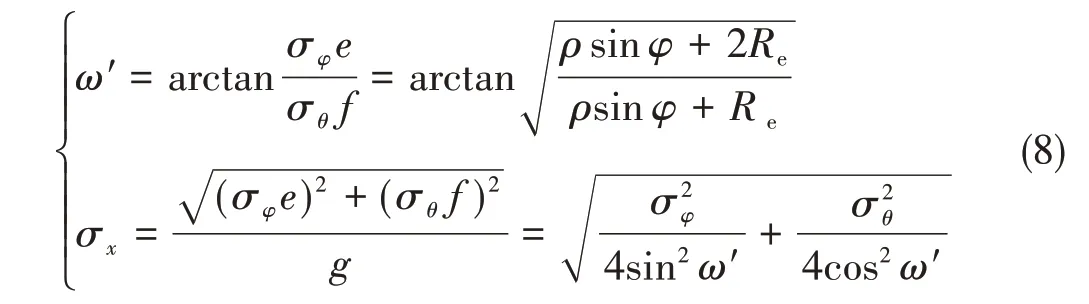
假定ω为帘线缠绕角，则合应力σx与复合材料主轴方向的偏轴角δ的表达式为

当复合材料微元模型受到偏轴角为δ的偏轴拉力σx时，根据应力转轴公式可解得复合材料的三向主应力σ1、σ2和σ12为[12]

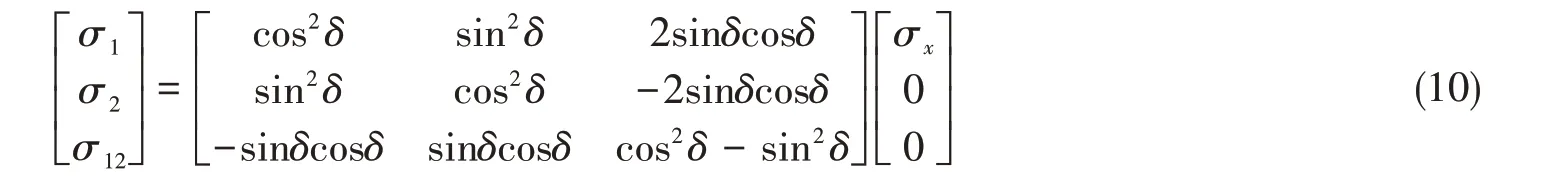
对于帘线橡胶复合材料，可以采用Tsai-Hill 强度理论进行失效判断[12]。Tsai-Hill 强度理论是基于各向同性屈服准则（MISES理论）的推广。Tsai-Hill的失效准则为

式中，X为帘线复合材料轴向拉伸强度，Y为帘线复合材料的横向拉伸强度，S为帘线复合材料的剪切强度。则由式（7）～（8）和式（10）～（11）可解得囊体的耐压强度Ps的表达式为

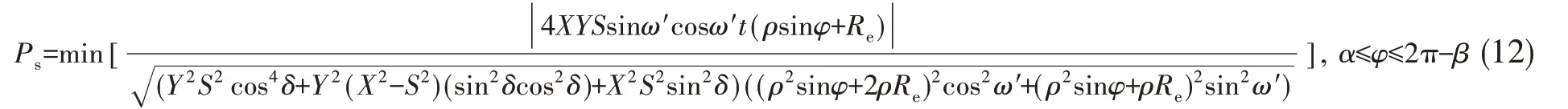
2.3 帘线缠绕角度的优化设计

帘线增强橡胶材料的三向主应力分别为轴向主应力σ1、横向主应力σ2以及剪切主应力σ12（主应力方向可参照图4），三向主应力方向对应的材料强度分别为轴向拉伸强度X、横向拉伸强度Y以及剪切强度S。对于帘线增强橡胶材料，轴向主应力方向（即沿帘线缠绕方向）对应的轴向拉伸强度远高于横向拉伸强度和剪切强度。因此，为提高囊体耐压强度，可以通过调整帘线的缠绕角度，使复合材料受到的主应力集中于轴向，此时计算得到的囊体的耐压强度为最大值，其对应的帘线缠绕角为最佳缠绕角γ。

现假定气囊的结构系数λ为囊体有效半径Re和波纹半径ρ的比值，其表达式为λ=Re/ρ。当复合材料受到的主应力集中于轴向时，可认为合应力σx与复合材料的主轴方向（即帘线缠绕方向）相同，此时，则可根据式（8）和式（9）计算囊体的最佳缠绕角γ，其表达式为

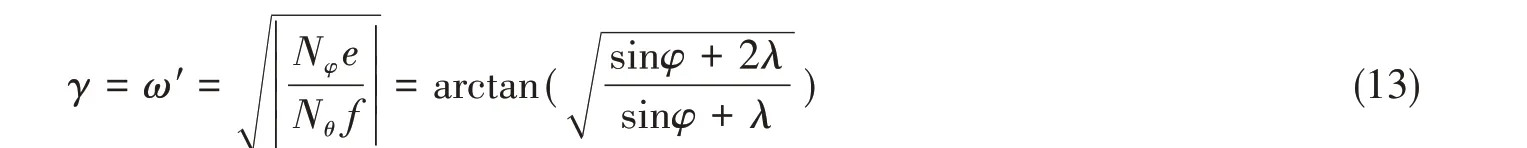
为保证气囊的承载性能，囊式气囊隔振器的结构系数λ应大于0，膜式气囊隔振器的结构系数λ应大于1，由此绘制不同结构系数λ下气囊的最佳缠绕角γ如图5所示。

由图5 可知，不同结构系数λ下气囊囊体的不同位置处的最佳缠绕角γ并不相同，但随着λ的提高，不同位置处的γ的变化越来越平缓。因此，在囊体设计过程中，考虑到后续帘线缠绕的工艺可实现性，应尽量提高气囊的结构系数λ来保证囊体不同位置处的帘线缠绕角更易接近最佳缠绕角γ。

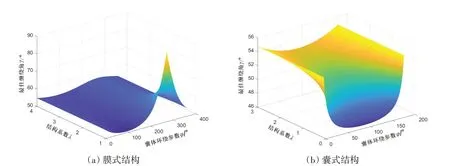
图5 气囊隔振器最佳缠绕角示意图Fig.5 Schematic diagram of the optimal winding angle of the air spring

3 试验验证

现选取某型气囊隔振器单层帘线增强复合材料进行拉伸试验，确定其三向拉伸强度X、Y、S。试验标准参照《GBT 3354-1999 定向纤维增强塑料拉伸性能试验方法》及《GBT 3355-2005 定向纤维增强塑料纵横剪切试验方法》。

试制单层帘线复合材料样件，样件由单向帘线层和橡胶构成。样件按照帘线的铺设角度分为三类，分别为0°、45°和90°，三类按照标准尺寸进行裁剪，试验样件如图6所示。

图6 拉伸强度试验样件Fig.6 Tensile strength test sample

通过拉伸试验机检测各试件拉伸过程中的最大拉伸力，假设00、450和900对应的最大拉伸力分别为W1、W2和W3，则可按式（14）计算复合材料的三向拉伸强度。

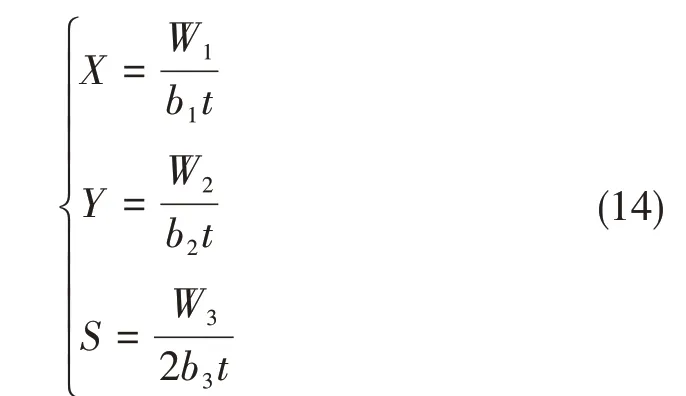
式中,b1、b2和b3分别为标准样件的宽度。试验结果如表1 所示，该型膜式气囊隔振器的具体参数如表2所示。

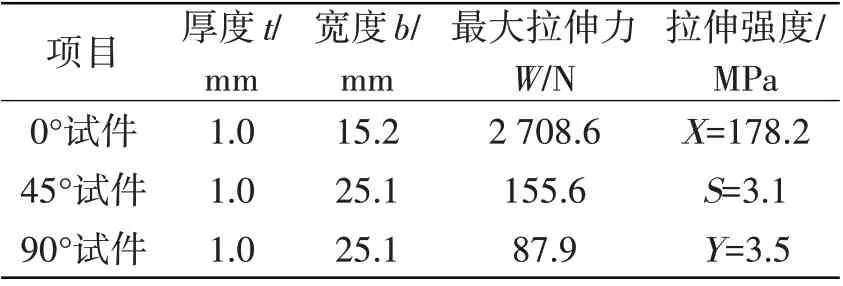
表1 单层帘线复合材料拉伸试验结果Tab.1 Tensile test results of single-layer cord composites

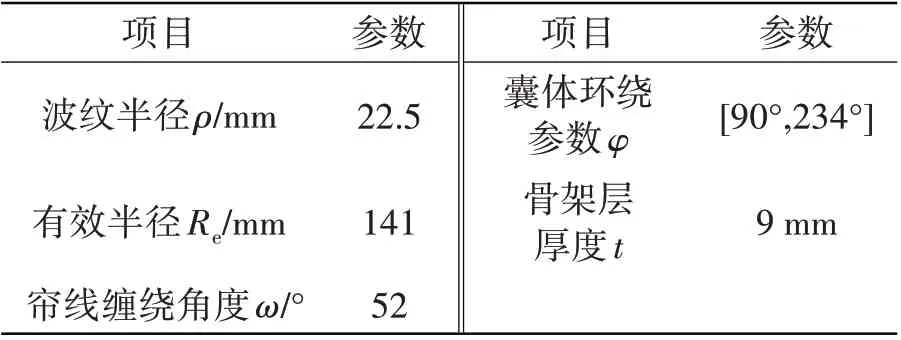
表2 气囊隔振器样机参数Tab.2 Air spring prototype parameters

根据耐压强度表达式可计算该型膜式气囊隔振器的囊体耐压强度为Ps=24.5 MPa。

对该型气囊隔振器进行爆破试验，试验如图7所示，试验爆破压力为27 MPa，相对误差为9.3%，理论计算与试验结果基本吻合。若按照式（13）计算得到的最佳缠绕角γ进行缠绕，囊体的耐压强度理论计算强度为90.6 MPa，此时囊体的耐压特性显著提高。但是在实际过程中，气囊的爆破压力不可能达到此值，这主要是由于帘线缠绕工艺性问题，各位置处的帘线缠绕角不可能完全按照最佳缠绕角缠绕，而囊体耐压强度将会取决于与最佳缠绕角偏差最大的位置。因此，在气囊设计过程中，可尽量按照最佳缠绕角γ设计气囊的帘线缠绕角度，同时还应提高结构系数λ来保证囊体不同位置处γ变化的平稳性，减小缠绕偏差值，提高囊体耐压特性。

图7 气囊注水爆破试验Fig.7 Air spring water injection blasting test

4 结 语

现有气囊隔振器的耐压强度理论模型仅针对某型气囊，且仅将帘线破坏作为其失效判断标准，其计算结果往往并不准确。本文通过薄壳无矩理论建立了囊式和膜式结构气囊隔振器的统一力学模型，结合复合材料的建模分析和Tsai-Hill强度失效理论，推导出气囊隔振器的耐压强度表达式。经试验验证，理论计算结果和试验结果基本吻合，为气囊的可靠性设计提供了重要的理论支撑。

气囊隔振器的耐压强度主要取决于囊体的帘线骨架层，而帘线缠绕角度将会极大地影响帘线骨架层的力学特性。因此，为保证囊体的耐压强度，结合囊体内力状态，推导出了不同结构系数λ下的最佳缠绕角γ的表达式。由于γ在囊体不同位置处并不相同，为保证最佳缠绕角γ的平稳性，降低实际缠绕角的偏差值，在气囊设计过程中应尽量增大结构系数λ。