船舶纵摇对内外桨水动力性能的影响分析

王文全，胡笑寒，王诗洋，张祥瑞

（1.中国船舶及海洋工程设计研究院，上海 200011；2.哈尔滨工程大学船舶工程学院，哈尔滨 150001）

0 引 言

螺旋桨工作于船尾部，由于船型尾部形状复杂、曲率变化大，推进器将受到船体运动后的伴流影响。进入桨盘面的水流速度及其分布（即桨盘面处伴流）受船体影响很大，与敞水情况完全不同。对于四桨两舵大型船舶，船尾附体较多，船桨干扰作用更加明显，船尾伴流更加复杂，内外桨所处的尾流场也有所不同。船舶运动使得船尾伴流场更加复杂，而船舶纵摇使得船后螺旋桨既有纵摇又有升沉，螺旋桨的运动变得很复杂，内外桨桨前伴流场会产生很大的变化，内外桨负荷受船体纵摇的影响很大。因此，研究四桨两舵船舶的船桨相互干扰，以及纵摇对船尾伴流场影响，可以为减小内外桨的负荷差以及船舶推进系统的设计、性能预报、设备布置等提供参考意见，具有重要的工程意义。

船体运动对于船后螺旋桨的影响可以通过采用强迫船体主动运动方法或船在流体作用下的被动运动方法来进行评估。关于敞水螺旋桨，其具有升沉运动、纵摇运动甚至于两者的叠加运动或者孤船六自由度运动，国内外的很多学者[1-2]都进行了研究计算。但是对于船桨一体的运动，由于需要处理运动船体、旋转螺旋桨之间的相互耦合作用与响应，船模运动中自航的CFD 模拟相当复杂，因而有一定数量的关于波浪中船舶运动响应和阻力增加CFD计算方面的文献[3-6]。

目前已发表的有关波浪中自航CFD 模拟方面的文献主要来自于美国IOWA 大学的Stern 团队。Carrica 等[7]开展了静水中带自由升沉、纵倾KCS 船模自航以及顶浪中船模运动响应的CFD 模拟，计算分析了模型自航点下，船模的升沉量、纵倾角和螺旋桨转速，以及规则波顶浪中船模的阻力和运动响应。文中并未开展船模波浪中自航的CFD 模拟，不过静水中船模带自由升沉、纵倾自航CFD 模拟，从技术层面来看，对波浪中自航CFD 模拟有一定的借鉴价值。Carrica 等[8]还采用CFD 模拟开展了随浪中船舶横甩机制的研究，文中进行了波浪中船舶自航的CFD模拟，虽然该论文更侧重于船舶操纵性和运动响应，但对船模波浪中自航CFD模拟无疑也有较高的借鉴和参考价值。

本文采用RANS 技术和重叠网格技术，针对具有四桨两舵船模，开展了静水中带纵摇的船模阻力和自航CFD 模拟。首先开展了静水中带纵摇的船体阻力模拟和静水自航模拟，并通过与模型试验结果的比较，初步验证了本文CFD模拟方法的准确性；随后开展了不同纵摇角度和纵摇周期的并耦合运动响应的船模自航CFD 模拟，对该种状态下船模的阻力、运动响应和船后螺旋桨的推力、扭矩等进行了分析，获得了有关变化特性。本文的研究工作，对于运动下多桨舰船快速性研究和预报等，具有一定的指导意义和参考价值。

1 理论基础

1.1 湍流模型

本文中计算应用的是RANS平均法，选用在船体周围流体流动数值模拟中应用较广的二方程SSTk-ω模型。

y+模型适用于对流减压区的计算，而且还将正交发散项列入考虑，扩大了该模型的适用范围，使其在近壁面和远壁面均适用。该模型主要应用于流体与固体表面分离的问题中，可以准确地获取固体表面流体的流动问题。这就要求在使用该模型时，网格要包含有边界层，且要有相当高的精度，特别是在固体表面附近，这就需要y+满足一定的要求。图1为近壁区域速度分层示意图。

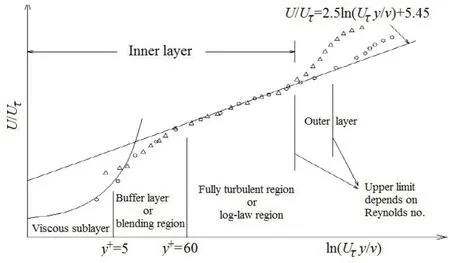
图1 近壁区域速度分层的划分Fig.1 Division of stratification near the wall

SSTk-ω的流动方程为

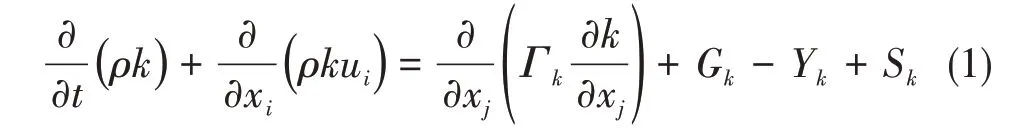
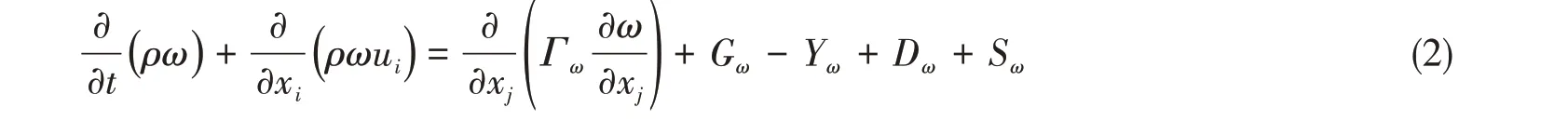
式中：Gk为湍流的动能；Gω为耗散率ω产生的动能；Γk、Γω为k与ω的有效扩散项；Yk、Yω为k与ω的发散项；Dω为正交发散项；Sk与Sω由用户自行给出。

1.2 重叠网格

重叠网格方法的最终目标是要建立各重叠(嵌套)网格间的耦合关系，为各区域流场计算提供边界信息的传递服务。因此，重叠网格方法可以简单地归纳为两个主要步骤：

（1）挖洞。若某重叠网格单元落入另一网格域的非可透面(NPS)内(如物面或初始洞边界面)，则应被标记洞内点，而不参与流场的计算。这一过程被形象地称之为“挖洞”。

（2）插值。在各网格域中分别寻找插值边界面的贡献单元(donor cell)，并通过贡献单元将流场解的信息插值到插值边界面网格上。

无论是挖洞还是寻找插值边界的贡献单元，找点的工作都必不可少。所谓“找点”，实际上是寻求某给定网格点与另一已知网格（单元）之间关系的过程。

2 静水中船模阻力与自航模拟

本文采用四桨两舵船模，船体几何模型如图2所示，其具体参数见表1。

图2 船体几何模型Fig.2 Geometry model of the hull

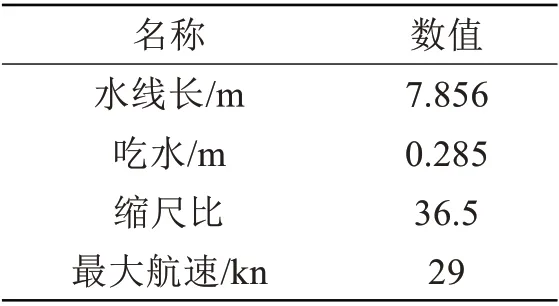
表1 船体几何模型参数Tab.1 Geometric parameters of the hull model

本文采用重叠网格技术，将船体包含在一个小域中，然后再建立一个适当的背景域，将小域的边界与背景域的交界面生成Interface，该Interface 边界条件类型设置成Overset Mesh Interface，使包含船体的小域按照设定的规则运动，同时在Interface 的两个边界面上实现非定常流场的数值传递。图3 为流体域网格。计算船模自航时，还要在桨轴后给内外螺旋桨分别创建一个圆柱形小域，小域与桨毂同轴，其直径等于1.2 倍螺旋桨直径，通过滑移网格方法模拟螺旋桨旋转运动。

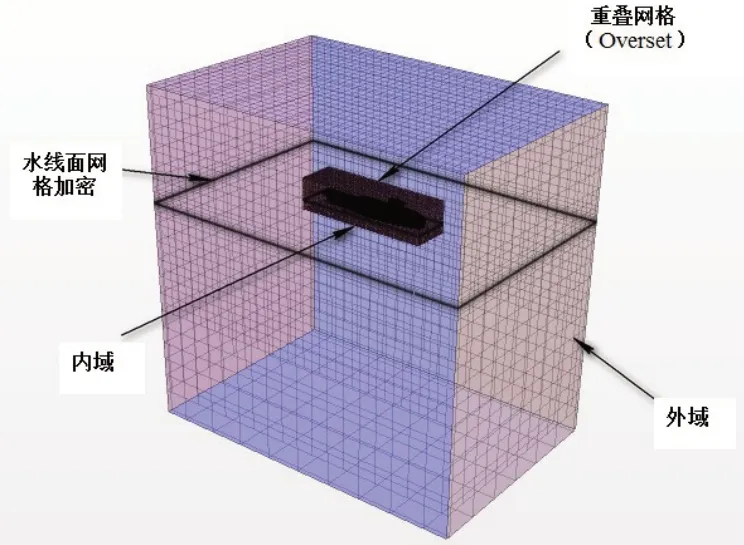
图3 流体域网格Fig.3 Fluid domain grid

2.1 船模静水阻力计算与分析

数值计算的船模阻力与阻力系数列于表2中，表中同时给出了模型试验结果。从表中可以看出，在此工况下，本文CFD 计算的船模阻力/总阻力系数与模型试验结果相当接近，二者之间的差别不超过5%，精度满足工程需要。

表2 船模静水阻力CFD计算值Tab.2 CFD calculation results of ship model hydrostatic resistance

图4 给出了船模静水中拖曳航行兴波CFD 计算结果，同时反映了船模静水中拖曳航行的兴波波系和波形，特别是艏波和肩波。图5 则给出了船模静水中拖曳航行边界层和尾伴流CFD 计算结果。从图中可以看出：在船模艉部收缩段以前，边界层附着在船模表面且保持稳定；在艉部收缩段以后，边界层急剧变厚，并形成尾伴流。

图4 自由液面开尔文Fig.4 Kelvin wave of free surface

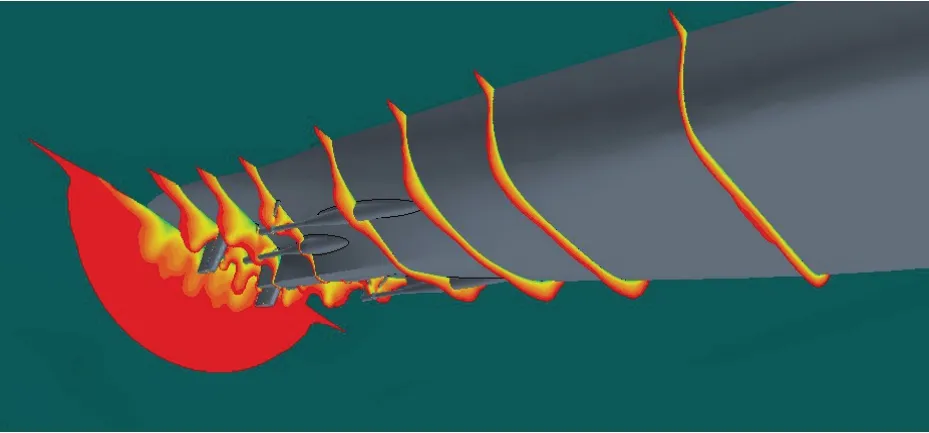
图5 船模静水中边界层和尾伴流Fig.5 Boundary layer and wake flow of ship model in still water

2.2 船模静水自航计算与分析

通过裸船阻力，可以验证Star-ccm+计算的准确性，因此可以将表3 中的自航计算的结果当做一个基本的参考值，与下面要进行的船体纵摇计算值进行对比分析，以说明船体纵摇对四桨水动力性能的影响。

表3 船体阻力和船后螺旋桨性能数值计算结果Tab.3 Numerical calculation results of hull resistance and propeller performance

图6 为船尾压力分布云图，由于水流的冲击作用，轴支架和舵的迎流位置处压力大，但随后即出现一定程度的流体分离，轴支架和舵两侧压力迅速降低形成低压区，有可能导致空化出现。

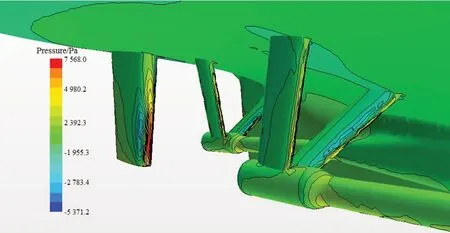
图6 船尾压力云图Fig.6 Pressure cloud diagram at the stern

图7为船体周围流体流线图，从图中可以比较清晰地看出水流的运动轨迹，船尾水流沿着船体型线向内收缩，由于船尾附体较多，主要是轴支架和舵的扰动，使得流线相对船首位置更加复杂。螺旋桨的旋转作用导致的流线变化可以清楚地从图中看出，无桨时，流线与船尾型线走向一致；有桨时，螺旋桨推水作用明显，流线在螺旋桨的作用下呈螺旋状径直流向下游。

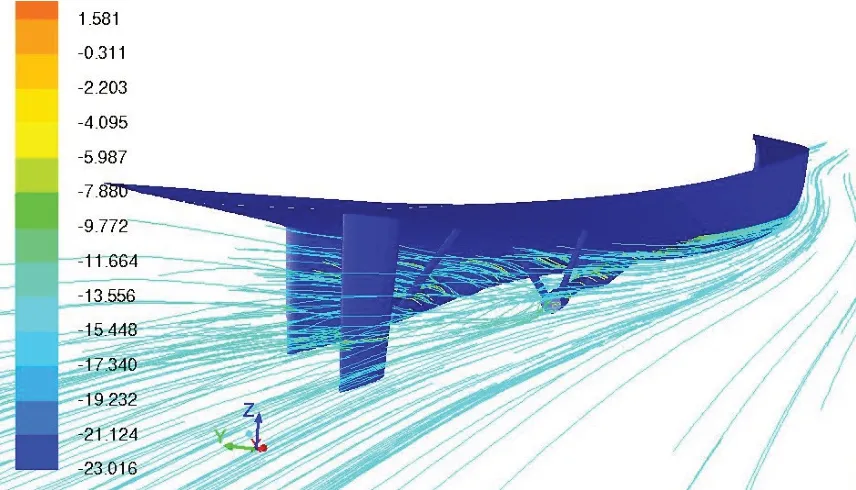
图7 船尾流线图Fig.7 Stern streamline diagram

3 船模纵摇运动下自航模拟

本文基于Overset 网格技术对船桨推进系统旋转与纵摇的耦合运动进行了数值模拟。计算过程中考虑了重力的影响，对该船桨推进系统在纵摇运动1.2°下，周期T=5 s 和T=10 s 两种工况下的水动力性能进行了计算和分析。船体纵摇运动的公式定义为

图8 给出了四桨推进系统在振荡运动状态下的运动示意图，图中标出了下文分析中会出现的四个时刻t/T=0.00（与t/T=1.00相同），t/T=0.25、t/T=0.5、t/T=0.75所对应的位置。

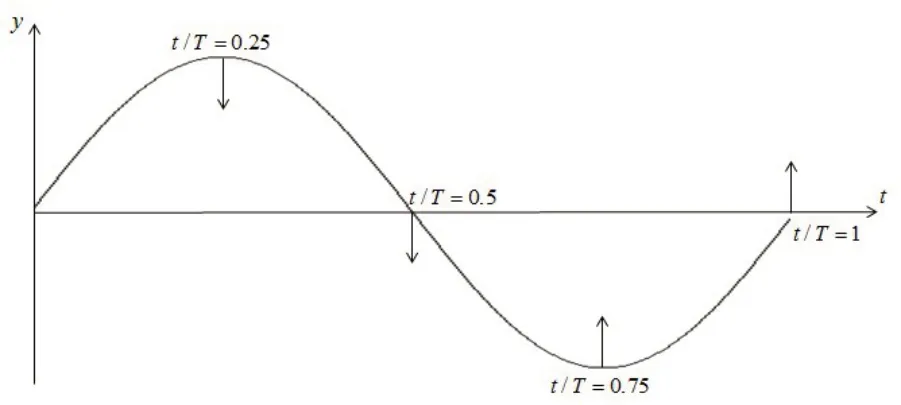
图8 船体纵摇运动示意图Fig.8 Schematic diagram of hull pitching motion

图9显示了自由液面的变化，图中蓝色与红色分别代表了50%的空气和50%的水，很好地显示了水汽交界面。从图中可以看出船体在一个周期内四个时刻的运动状态，船体在一个周期内分别经过了平衡位置、艏倾、平衡位置与尾倾四个状态。通过对比发现，艏倾与尾倾明显引起艏尾两侧流场变化。

图9 船体运动状态示意图Fig.9 Schematic diagram of hull motion state

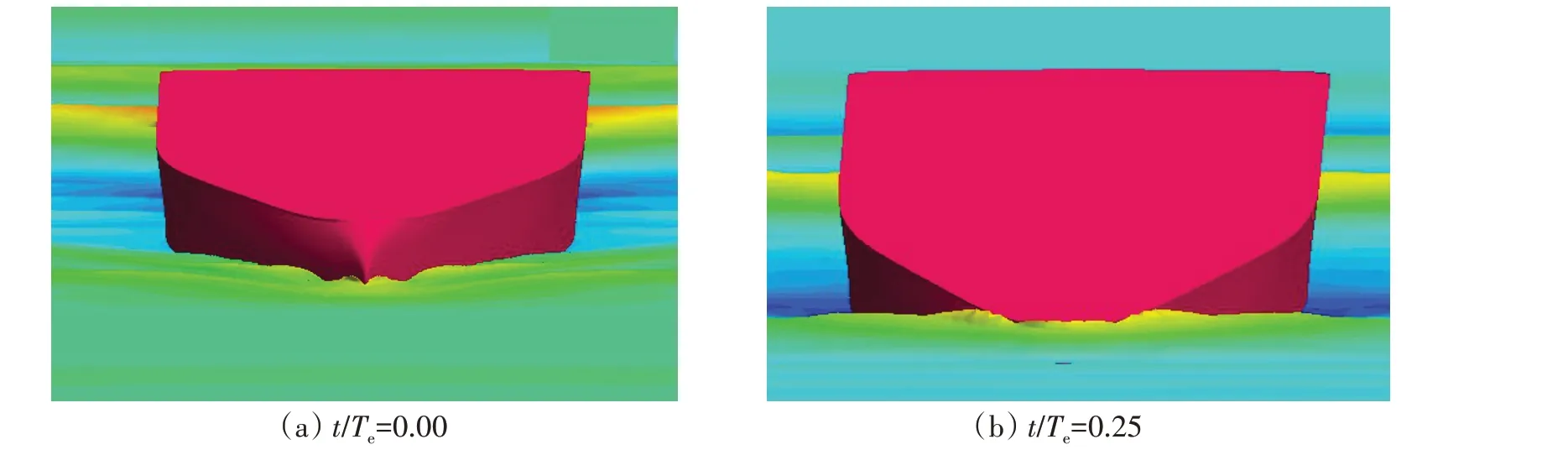
图10中4张图分别代表了一个周期内船首的四个运动状态：平衡位置（船首有向下运动的趋势）、艏倾、平衡位置（船首有向上运动的趋势）和尾倾。从图中可以清晰地看出船舶在行驶过程中会产生明显的艏波，同时船体的纵倾与尾倾使艏波变得更大。

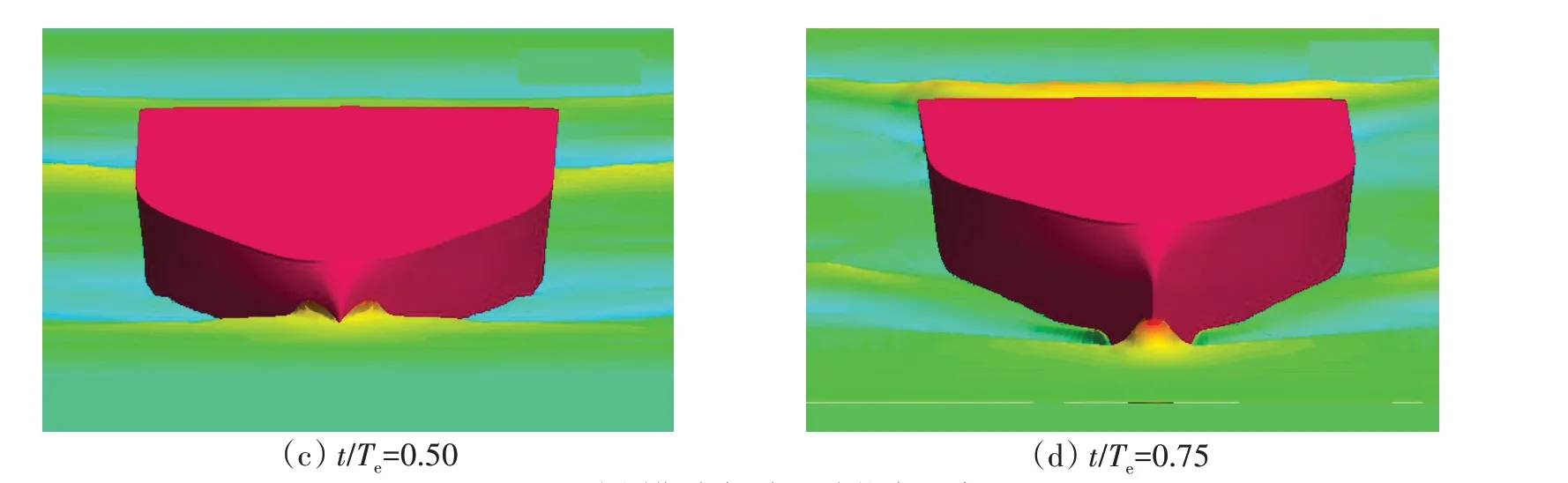
图10 一个周期内船首运动状态示意图Fig.10 Schematic diagram of the bow motion state in one cycle

分析图11～13可以得出如下结论：

（1）通过图11可以发现，船体在艏倾与尾倾时阻力最大。随着船体纵摇周期的变大，船体阻力变化越来越不明显，阻力的峰值也变得较小。由于船体纵摇周期的增大，船体摇动的速率变小，因此由船体运动额外兴起的波浪减少，波浪增阻较小。

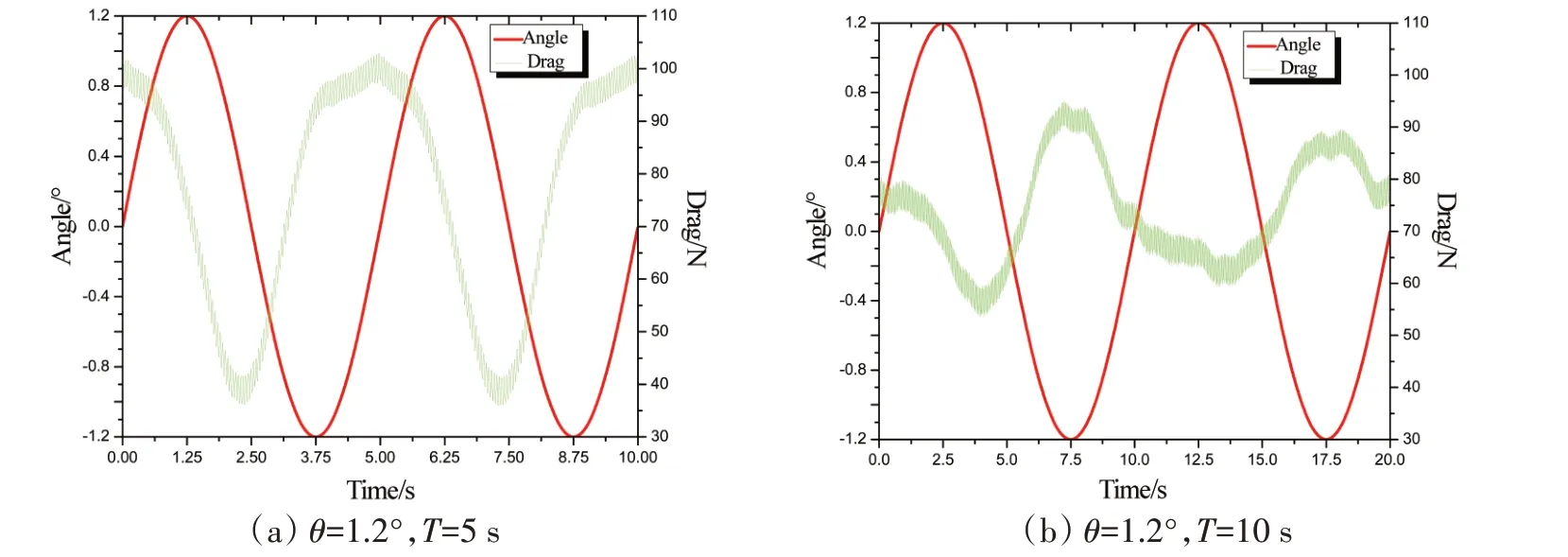
图11 船体阻力随时间变化曲线Fig.11 Hull resistance changes with time

（2）通过图12 可以发现，推进系统（推力）的非定常特性十分明显，且呈类正弦曲线变化规律，可以看出内桨的变化规律不受船体纵摇周期的影响，外桨在不同的纵摇周期变化很明显，但是总体数值变化不大。说明船体在纵摇的过程中，外桨处的流场变化更剧烈。

图12 内外桨推力随时间变化曲线Fig.12 Thrust curve of the inner and outer propellers varying with time

（3）通过图13 可以发现，推进系统（转矩）的非定常特性十分明显，且呈类正弦曲线变化规律，转矩的变化周期与船体纵摇的周期一致。当船体从平衡位置开始艏倾时，内外桨转矩增大，最大艏倾角时，转矩最大。船体从最大艏倾位置向最大尾倾位置运动时，内外桨转矩同时减小，内外桨可以认为在最大尾倾位置转矩达到最小。船体在从最大尾倾位置向平衡位置运动时，内外桨转矩同时增大。当船体运动到平衡位置时，船体运动经过一个完整的周期。

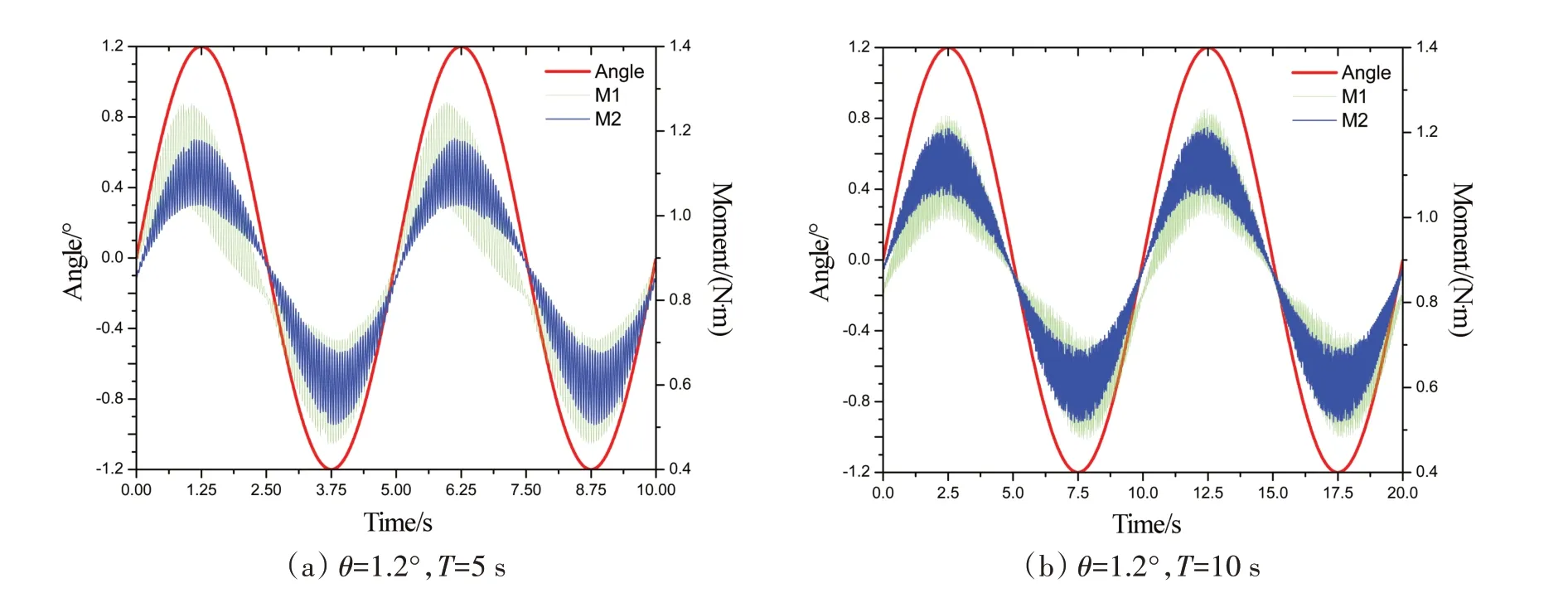
图13 内外桨转矩随时间变化曲线Fig.13 Torque curve of inner and outer propellers varying with time

螺旋桨在船尾三向非均匀伴流场中工作时，以轴向伴流分量为最大，径向和周向分量相对较小，所以应重点分析船尾桨盘面处的轴向速度分布情况。图14所示为内外桨盘面处轴向速度（左侧为外桨）分布情况，由图可知，内外桨盘面处轴向速度变化基本一致，桨叶叶梢附近存在明显的速度闭合区，整体的伴流分数分布和桨叶数存在着一定联系，等值线在桨叶附近呈径向外凸，倾斜方向与桨叶旋转方向一致。

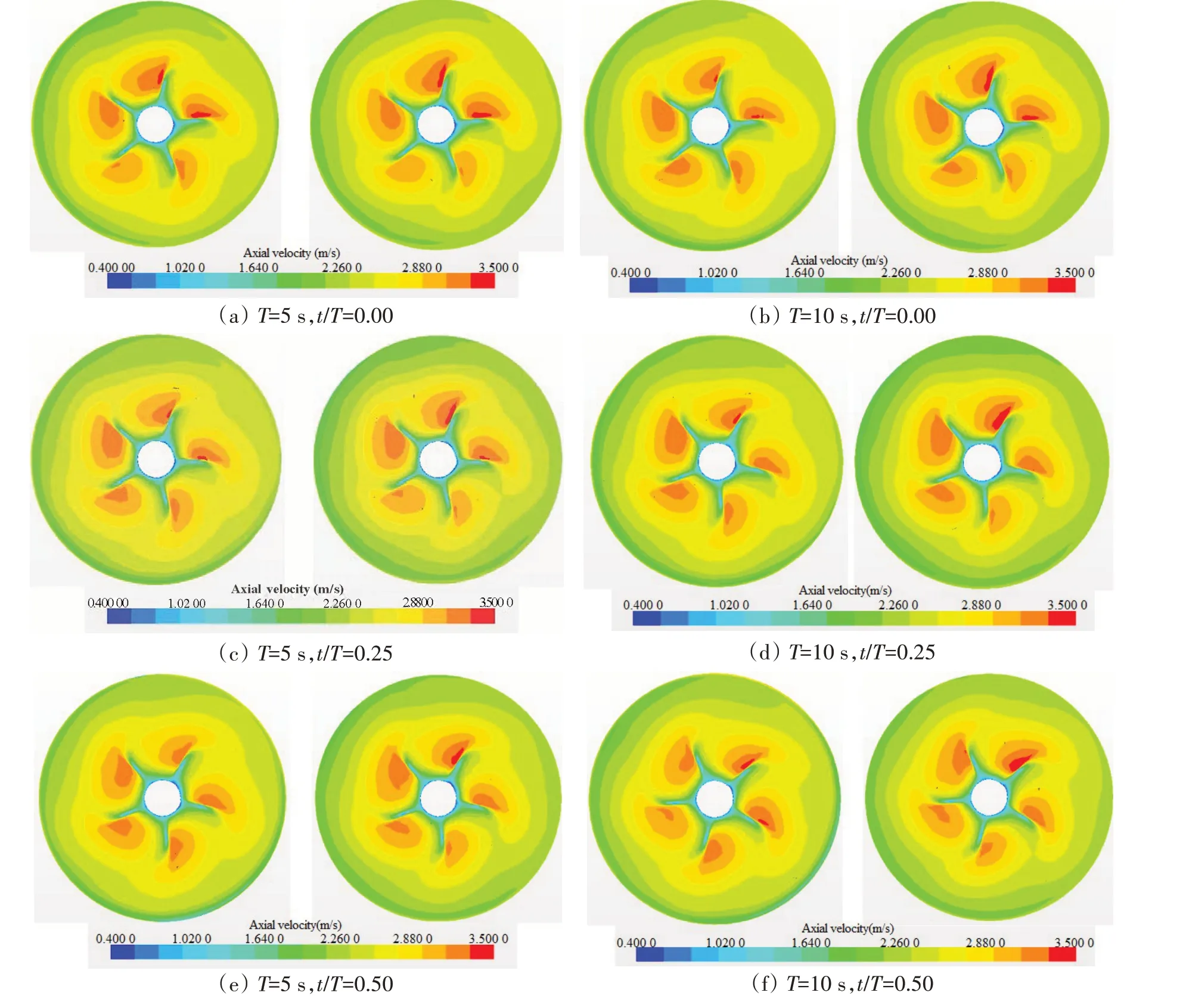
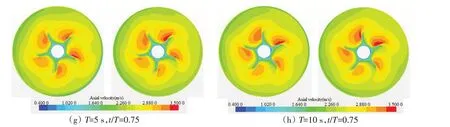
图14 不同时刻内外桨盘面处轴向速度Fig.14 Axial velocity at the inner and outer propeller surfaces at different times

4 结 论

本文采用基于RANSE 的数值波浪水池和数值拖曳水池技术，开展了四桨两舵船模在纵摇状态下的自航CFD模拟研究。通过对计算结果的分析，可以得出以下结论：

（1）根据静水中的船模阻力和自航CFD模拟结果及与模型试验结果的比较可以发现，无论是船模阻力还是自航CFD模拟结果，均与模型试验结果符合良好，初步验证了本文的CFD模拟方法的准确性；

（2）船体纵摇周期对船体阻力和螺旋桨的推力影响很大，减少船体纵摇频率能有效地降低船舶阻力；

（3）与静水中相比，船模在纵摇中自航时，螺旋桨的推力和扭矩都有一定程度的变化，因此在设计船舶螺旋桨时应该考虑船舶运动时的状态，才能使螺旋桨达到最大效率。

本文的研究工作为波浪中舰船快速性研究提供了一种有效的技术手段；相关研究结果和结论，对于波浪中舰船快速性研究和预报等具有指导意义和参考价值。