船尾外形对超声速弹丸减阻特性的影响研究

邵 山，谭献忠，王学德

(南京理工大学 能源与动力工程学院， 南京 210014)

1 引言

弹丸的气动外形是影响其射程及外弹道稳定性，进而影响弹着点密集度的主要因素。通过优化弹丸的气动外形，有效减小弹丸飞行阻力，是一种有效提高射程的方法。对于超声速弹丸，阻力的构成主要包括激波阻力、摩擦阻力和底部阻力等3个部分。弹丸超声速飞行时，空气受到头部压缩出现头部激波，激波后压力增大，从而形成激波阻力。空气与弹体表面接触，由于粘性的作用，产生摩擦阻力。弹体尾部气流在弹底发生大角度转折，形成膨胀波。弹体尾部气流经过膨胀折转后，由于上下表面超声速气流方向的不一致，在距离弹尾不远处会发生再次压缩，形成尾部再压缩波，又称尾部激波，如图1所示。同时由于弹尾的存在，边界层会在底部分离，形成的回流区。回流区气压低，从而造成前后压差，形成底部阻力。

图1 弹丸底部流场结构示意图Fig.1 Schematic diagram of projectile base flow

相关研究指出，弹丸的形状影响着上述各阻力的阻力系数。从阻力的构成来看，头部激波阻力和底部阻力是弹丸阻力的主要因素。对于头部激波阻力可以通过优化弹丸的头部外形进行减阻[1]；而对于底部阻力，往往通过采用优化弹丸尾部结构和几何参数来进行减阻设计，如底凹结构设计方案[2-6]、不同底部平面形状设计方案[7]和不同船尾角设计方案[8-13]。其中，船尾角设计方案为弹丸减阻设计的经典方案。根据空气动力学理论，船尾角的存在一定程度上会减小底部回流区的大小从而降低底部阻力，但同时也会增强弹丸底部的真空度和尾部再压缩波的强度，从而一定程度上又会增加底部阻力。尾部再压缩波的位置也随着船尾角的变化而变化。理想状态下，尾部再压缩波前驻点距离弹底越远，对底部的影响也就越小。对于船尾外形，一定存在一个最佳角度既可以填补无船尾的缺点，又能够避免尾部再压缩波的加强导致的阻力增加。

弹丸的尾部长度和船尾角度，可以视为弹尾形状函数的2个自变量，对于给定长径比的弹丸来说理论上存在最优解，即存在最佳的船尾外形使得减阻效率最大。为此，本文中将在一确定尾部长度的前提下，利用计算流体力学的数值模拟方法[14-15]，通过对带不同船尾角外形的弹丸超声速流场的数值仿真，进而分析弹丸绕流流场结构和阻力的变化特性，研究弹丸船尾角的减阻机理和船尾角对弹丸减阻效率的影响规律。

2 弹丸模型与网格生成

本研究对象为122 mm弹丸，其头部、圆柱部、全弹长、长径比、收缩比和船尾角度的几何参数如表1所示，共选取0°、5°、6°、7°、8°、9°和10°船尾角进行了建模和数值计算。

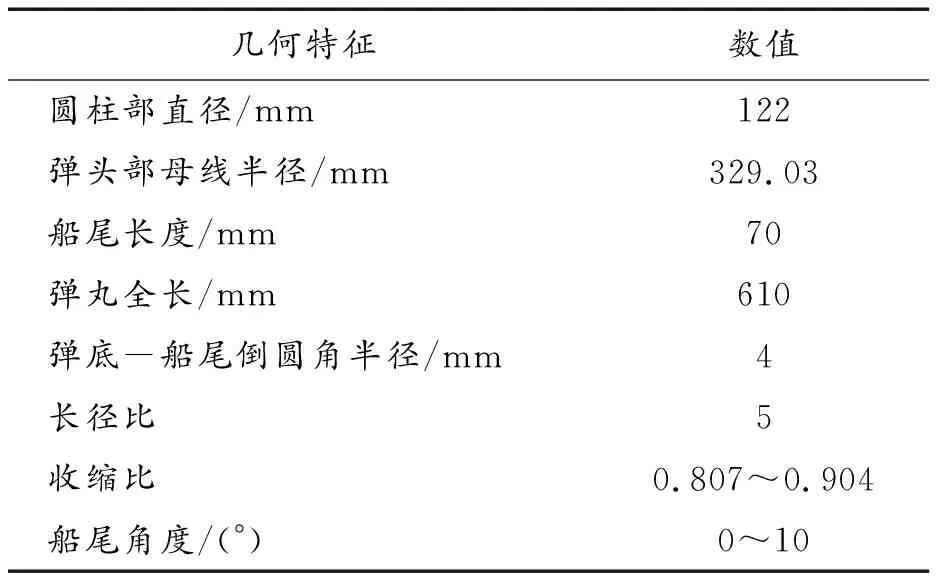
表1 物理模型的几何参数

网格生成的质量对流场的计算精度有着重要的影响，为提高网格生成质量，将流体分成3个区域，分别是前体、后体和加密区。为了提高求解速度同时保证计算精度，在加密区进行了加密处理。研究船尾附近及其后部的流场的特征是完成本次数值模拟的关键，故在弹体壁面以及弹体尾部中预先设定好加密区，以便于生成质量较高的网格，图2为本文所生成的计算网格，加密网格分布符合气流的流动规律。总网格数量在75万个左右，其中99.9%的网格质量值小于0.5，满足计算精度也兼顾了计算速度。

图2 弹丸流场计算网格示意图Fig.2 computational grids of projectile flow field

3 数学模型与计算方法

数学模型采用积分形式的Navier-Stokes方程，即：

(1)

计算方法采用有限体积格式，对流项采用Van Leer+AUSM耦合的逆风格式，湍流模型为S-A一方程模型，该模型由一个方程组成，对于近壁面边界层中黏性较大的流动区域，其计算效果较好，适用于超声速流动的外流流动问题。

4 计算结果与分析

4.1 不同船尾外形的流场和减阻特性

为了研究不同船尾外形的流场和减阻特性，本文首先数值模拟了无船尾和带5°、6°、7°、8°和9°等7种不同船尾外形的流场和减阻特性。图3给出了来流马赫数为2，攻角0°情况下，带船尾角7°外形和无船尾角外形密度云图。

图3 船尾外形和无船尾外形流场密度云图Fig.3 Comparison of density contours between boattail and non-boattail projectile

从图3中可以看出，船尾弹弹底的低密度区域更小，弹丸底部的低压区域更小。这样在与来流压力进行比较时，船尾弹的前后压差将会较小，从而达到降低阻力提高射程的目的。

表2给出了0°攻角下不同船尾角弹丸外形的阻力统计。从表2中可以看出：船尾阻力随船尾角度的增大而增大，弹底阻力随着船尾角度的增大而减小；弹丸总阻力随船尾角度的增大先减小后增大，在7°船尾角时总阻力最小，故选取7°船尾外形作为最佳外形。

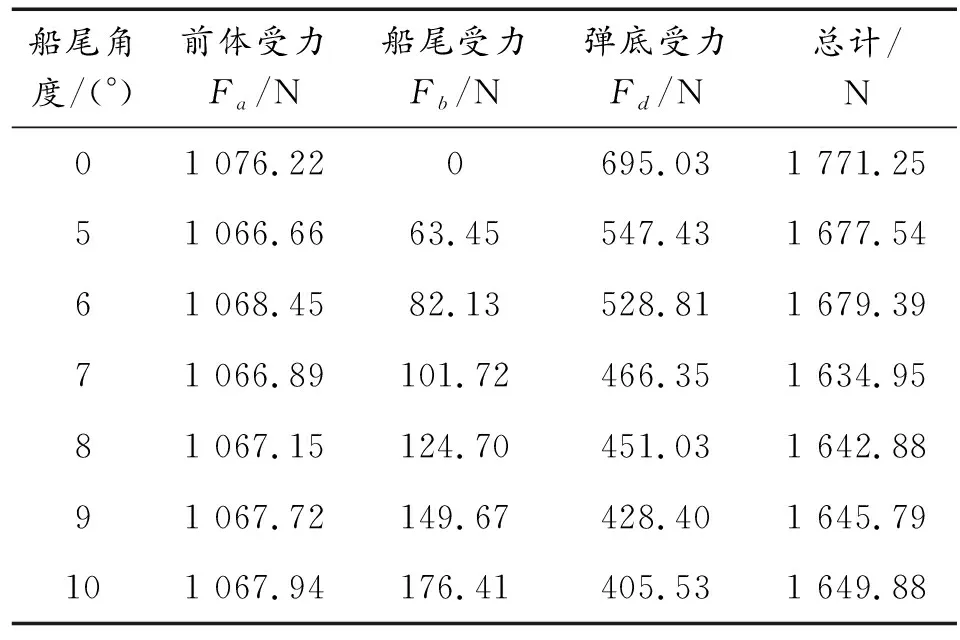
表2 不同船尾角弹丸外形的阻力

4.2 不同马赫数下船尾外形的减阻特性

122 mm炮的初速一般不会超过3马赫，因此本文数值模拟的马赫数范围为1～3。在不同马赫数情况下，对7°船尾弹丸进行数值计算，研究不同马赫数下的减阻效率，同时和无船尾外形进行了比较。计算结果如表3所示，从表3中可以发现：在超音速条件下，马赫数越大，船尾的减阻率越低。主要原因马赫数增大后弹丸的阻力构成中激波阻力的占比越来越大，且弹丸的尾部再压缩波越来越强，导致其减阻能力降低。

表3 7°船尾外形不同马赫数下的减阻比较

4.3 不同攻角船尾外形的流场和气动特性

在有攻角条件下，弹丸的气动特性主要体现在激波形状、弹体表面附面层状态以及弹底回流区的气流分布状态，与零攻角时有较大区别。为此我们研究了7°船尾外形在马赫数为2和0°、2°、4°、6°和8°等不同攻角下的气动特性。

图4为不同攻角下弹丸底部的流线图。有攻角时，弹丸在飞行过程中产生升力，同时改变了弹体附面层的气体流动特性：受到压力影响，弹体上表面的附面层厚度随着攻角的增大而增大，下表面与之相反，从而导致了上表面的附面层更容易发生分离现象；同时弹底回流区的对称性消失，气流速度迹线、矢量也发生改变。随着攻角的逐渐增大，回流区的上下2个漩涡逐渐偏离弹丸轴线。呈现出上部漩涡更大、但速度更慢的现象。船尾处上表面的附面层厚度更厚，在弹底处发生大角度偏折后气流更容易进入回流区，从而加强了此处的漩涡。与零攻角时相比，尾迹区的汇流处也逐渐向下移动，从上部引流而来的气流偏折程度逐渐增强。

图4 不同攻角下底部尾迹区内的流线图Fig.4 Wake flowof different attack angles

图5、图6和图7分别给出了7°船尾外形在马赫2速度下不同攻角的升力系数、阻力系数、升组比的变化曲线。从图5～图7中可以看出，在所计算的0°～8°的攻角范围内，该弹丸的升力系数随攻角增加而呈现近似线性增加的变化趋势，阻力系数随着攻角的上升而呈现近似抛物线上升的规律趋势。有攻角条件下，阻力系数增大是因为此时弹丸底部压强的减小，增大的前后压强差，导致阻力上升，由此可以得出结论：有攻角时该型弹丸的阻力系数略有增加，升力和升阻比随攻角呈现近似线性增大的变化规律。

图5 升力系数随攻角变化曲线Fig.5 Variation of lift coefficientwith the angle of attack

图6 阻力系数随攻角变化曲线Fig.6 Variation of drag coefficient with the angle of attack

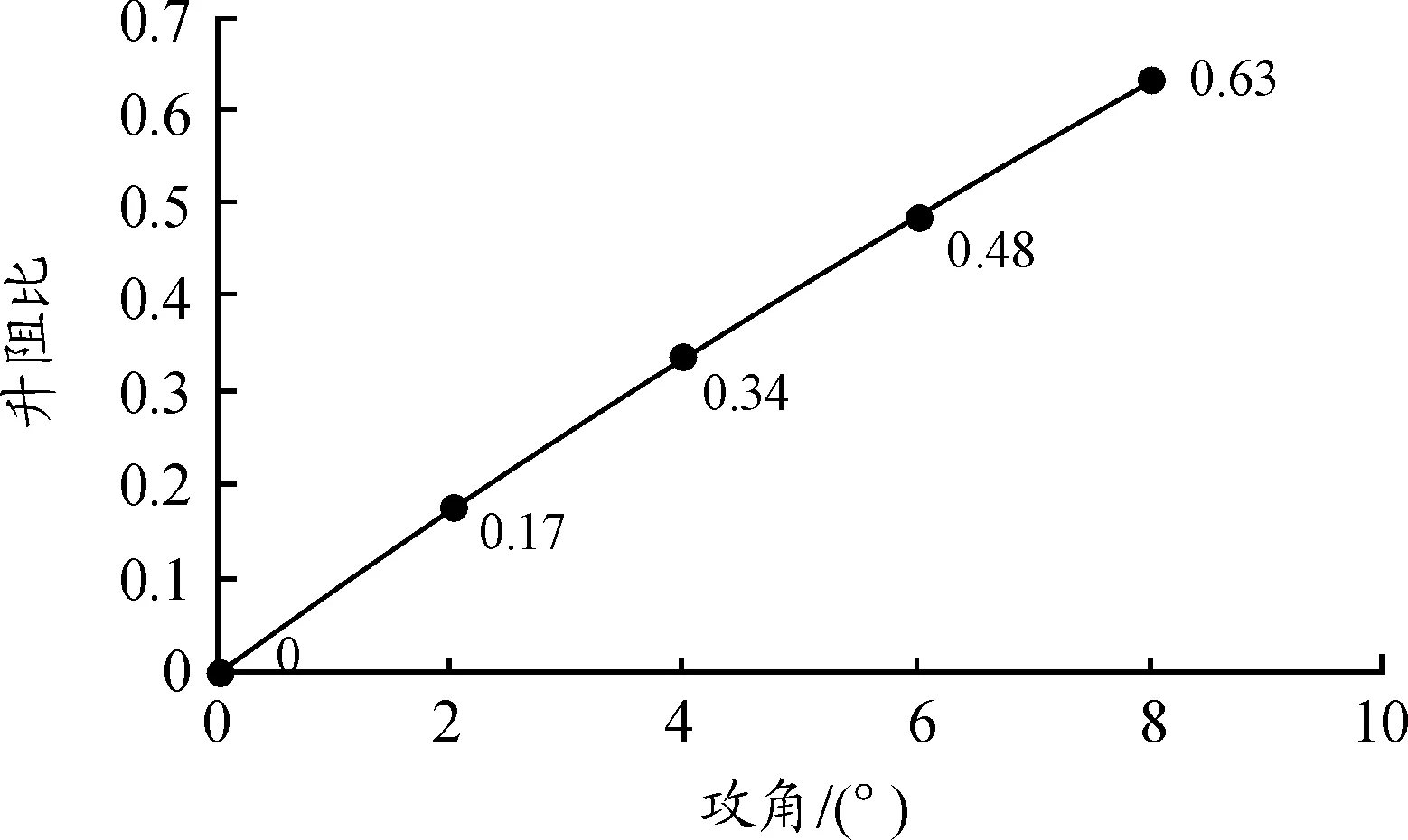
图7 升阻比随攻角变化曲线Fig.7 Variation of lift-to-drag ratiowith the angle of attack

5 结论

1) 带船尾外形可以明显降低底部回流区的大小，但也会增加底部的真空度和尾部再压缩波的强度。在零攻角下，7°船尾角的减阻效果为最佳，与无船尾弹相比，7°船尾角度的外形可以减阻7.75%。

2) 在马赫数为1时，7°船尾外形弹丸的处于跨音速的临界状态，此时底部阻力占比较大，7°船尾的减阻率为22.41%。随着马赫数的增加，弹丸受激波阻力的影响较大，由船尾外形提供的减阻效果逐渐减弱。

3) 在0°-8°的攻角范围内和马赫数为2工况下，带7°船尾外形的弹丸阻力系数随攻角增加而近似抛物线增加；升力系数和升阻比随攻角增加而呈现近似线性增加的变化趋势。