圆锥曲线平行弦的一组新性质探源

蒋道波 (安徽省蚌埠第二中学 233000)

蓝贤光老师在文[1]提出了圆锥曲线平行弦的一组新性质，笔者经过仔细思考，发现这一组性质本源实际上是圆锥曲线直径的性质．圆锥曲线的直径，就是无穷远点关于圆锥曲线的有穷远极线，关于圆锥曲线的直径，我们有如下定理：[2]

定理 直径是圆锥曲线的一组平行弦中点的轨迹．

下面给出蓝贤光老师所提的性质1和性质2的一个新的几何证明，证明的过程其实也是解释笔者所做出的判断的过程.首先观察文[1]的性质1：

性质1如图1，设OP是以点O为顶点的抛物线的顶点弦，弦MN与OP平行，且直线MN交抛物线C的对称轴于点T(异于点O)，则 |TM-TN|=OP(当点T为弦MN的内分点时)或|TM+TN|=OP(当点T为弦MN的外分点时)．

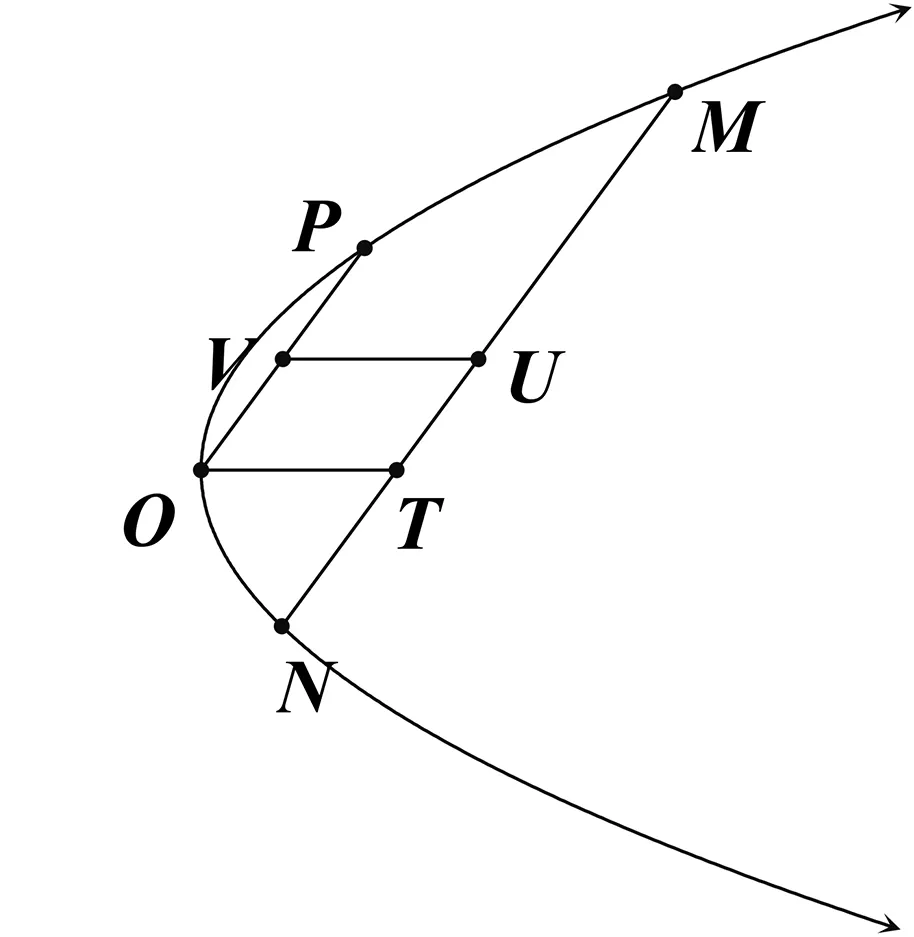
图1

证明设U为MN的中点，V为OP的中点，根据直径的性质，结合抛物线与无穷远直线相切，可得直线UV与直线OT平行．

(1)当点T为弦MN的内分点时，|TM-TN|=2TU，且OP=2OV，结合平行四边形OTUV的性质，TU=OV，所以|TM-TN|=OP．

(2)当点T为弦MN的外分点时，|TM+TN|=2TU，且OP=2OV，结合平行四边形OTUV的性质，TU=OV，所以|TM+TN|=OP．

接下来，对文[2]所提出的性质2进行解释．

图2

证明设U为MN的中点，V为OP的中点，根据直径的性质，直线UV经过椭圆的中心O．

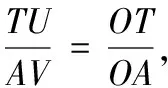
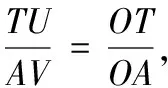
至于文[1]提出的性质3：

读者可以仿照笔者关于性质1和性质2所给出的解释完成论证，本文不再赘述．

通过上面的证明过程可以发现，文[1]的圆锥曲线平行弦的一组新性质的源头确为圆锥曲线直径的性质.