关联:数学课堂的应然追求
——以苏科版“线段、射线、直线(1)”的教学为例
何丽华 (江苏省金坛段玉裁初级中学 213200)
金杨建 (江苏省无锡市天一实验学校 214100)
数学知识在教材中是以“点”的形态呈现的.但各知识之间始终处于一种相互联系、相互依存、相互作用的状态[1],在系统论中称之为“关联”,亦叫“相关”.它主要表现在系统内部要素之间、要素与整体之间以及系统整体与外部环境之间的有机关联.构建数学知识的关联,实现“连点成线”“连线成面”“勾面成体”[2]是数学课堂的应然追求.
义务教育苏科版教材七年级上“6.1线段、射线、直线(1)”一课,知识繁多、概念零散,教学要求高、设计难度大.因此,教师在备课时往往缺乏整体设计,忽视逻辑连贯,授课时又疲于完成教学任务,缺少教学主线.本文以该课的课堂教学为例,从落实数学课堂“关联”的视角切入,阐释笔者的实践与思考.
1 情境入化 生活数学见关联
“数学”作为一个系统,“生活”则是这个系统的外部环境,而情境是连接两者的桥梁,也是问题冲突的开始.教师需要设计较为巧妙的情境,使学生在原有生活经验的基础上展开学习,实现学生生活常识与数学知识的无缝对接.
例如,课堂伊始创设了如下情境:
问题(1)请你观察从甲地到乙地的3条路,哪条最近?

图1
(2)从甲地到乙地能否修一条最短的路?如果能,请在图中画出这条路.
“数学来源于生活”,从生活出发,学生经历了从物到形的抽象过程,并且感知线段有两个端点;同时借助生活经验得到了基本事实——“两点之间,线段最短”.
再如,讲完线段、射线、直线概念后,教师出示如下问题:
生活中哪些事物可被“看成”线段、射线?哪些事物给你一种直线的感觉?
“让数学回归生活”,培养学生用数学的眼光观察世界,感受生活中处处有数学.
又如,我们可以利用“人名”在生活中的作用,让学生感受到三线表示方法的必要性.这种生活经验的正迁移,使知识的产生更加自然、知识的内涵更易于为学生接受.
从生活中来,到生活中去.将数学教材中枯燥、脱离学生实际的知识还原,使之生活化,从而沟通数学与生活.这种“关联”体现了数学和生活的整体统一,消除了学生对数学知识的陌生感和排斥心理,更能引起学生的共鸣,激发学生学习数学的兴趣.
2 本质深化 知识内部凸关联
“数学是由简单明了的事项与逻辑推理的结合而一步一步地构成的,所以,只有学习数学的人注意老老实实地一步一步去理解,并同时记住其要点,以备以后之需用,就一定能理解其全部内容.”[3]关联宜从“知识点链”入手,揭示前后知识之间的本质联系.
例如,中学阶段的“距离”概念,既是平面几何中的重要内容(初中阶段有“两点之间的距离”“点到直线的距离”“平行线之间的距离”等),又是立体几何中的核心知识(高中阶段有“点面距离”“线面距离”“面面距离”“异面直线间的距离”等).这些距离概念的共性就是两个点集的元素之间的最小值;其概念蕴含了四个数学性质——非负性、同一性、对称性和最小值[4].
这四个性质中,最小值是距离概念的本质属性.在教学中可以通过图2所示结构,使基本事实1(两点之间,线段最短)和重要概念(两点之间的距离)之间的关联得以凸显.
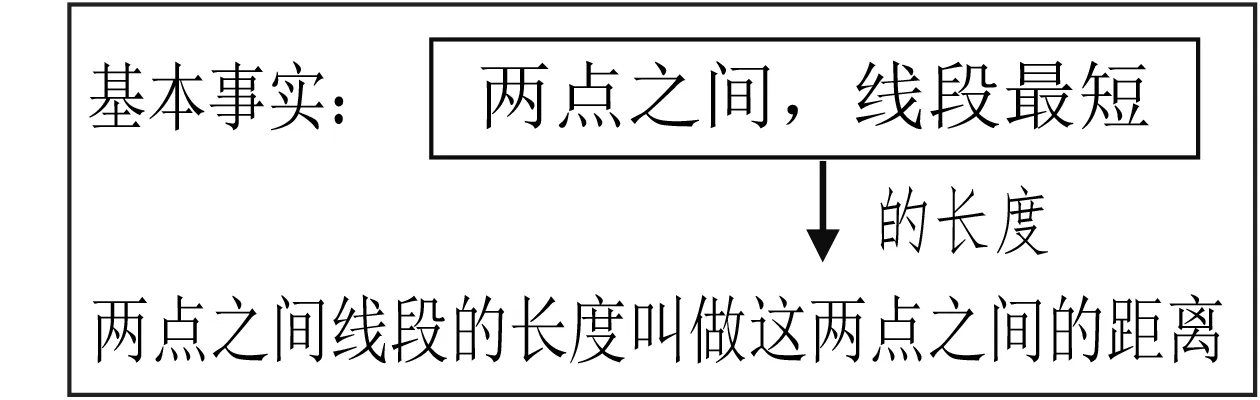
图2
再如,在基本事实2(两点确定一条直线)教学之后,设计如下问题串:
(1)将一根细木条固定在墙上,至少需要几个钉子?
(3)画图题:如图3,已知点A,B,C.
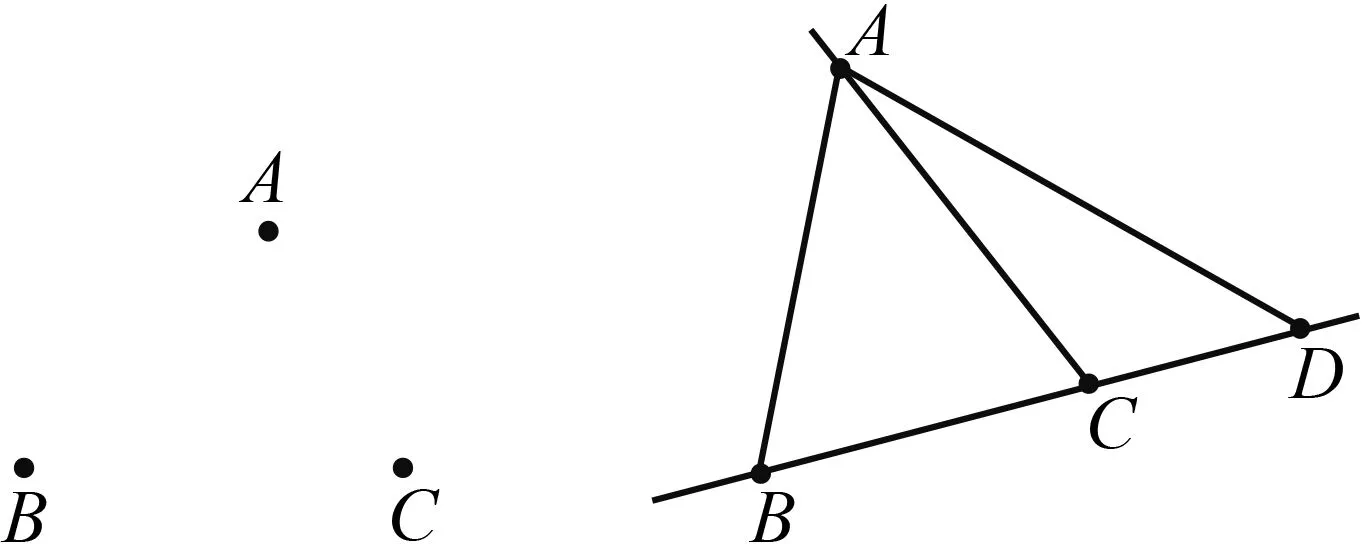
图3 图4
①画线段BC(连结BC),画直线AB,AC;
②在线段BC上取一点D,画射线AD.
(4)说图题:请用语言叙述图4的画图过程.
问题(1)主要是基本事实2的工具性理解[5],而问题(2)(3)分别达到了基本事实2“表示方法”与“画图”之间的关系性理解[5],问题(4)使结论变得更加开放,从而达到了知识之间的创造性理解[5].
挖掘知识本质,揭示知识之间内在联系,让学生感受到“数学是连贯的,它是一张编织紧密的挂毯,其中所有概念和技巧逻辑严密地编织在一起,形成一个统一的整体”[6],从而容易实现对数学基本结构的掌握.这种活动经验的积累是数学课堂教学的关键之处,而这恰是平时教学时易于忽略的.
学习数学的目的是为了应用数学.在完成教材中简单的例题教学之后,教师可进行变式和拓展,提出更为深刻的问题.如:函数y=lnx+2x-6存在几个零点?
3 图形活化 变式教学显关联
几何,简言之,就是研究图形的形状、大小与位置的学科.因此学好几何必须有“图感”,即不仅要学会读、识、画、作简单图形,还要善于将复杂图形分解为简单图形.课堂教学中可通过灵活变化图形达成这一目标.
比如,在例题教学中安排如下例题及其变式:
例1如图5,(1)以A为一个端点的线段有条,它们是.以B为一个端点的线段有条,它们是.
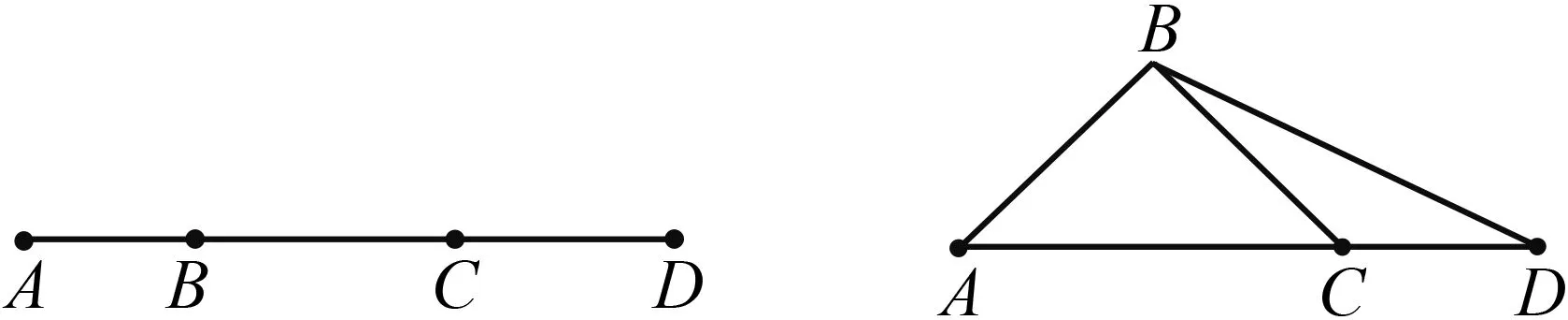
图5 图6
(2)图5中共有多少条线段,请分别表示出来.
(3)判断:点A、点C之间的距离是线段AC( ).
图7
图形变式2:多媒体演示运动变化过程得到图7,
(1)图中共有多少条线段?
(2)判断:射线AC与射线AD是同一条射线( ).
(3)判断:射线AC与射线BC是同一条射线( ).
(4)共有几条射线?能表示的射线有.
解后反思:通过例题及其变式,你有哪些感悟和收获?
创新变式3:如图8,你能提出哪些问题?
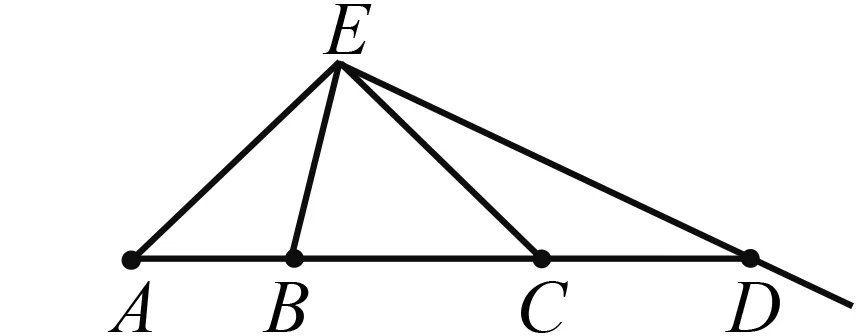
图8
两个“图形变式”,让“死板”的图形“活化”起来,有利于学生理解图形及图形间的关系,感悟其本质,形成“图感”.而“创新变式”培养学生发现问题、提出问题的能力.这样的变式教学,打破藩篱,开拓思维,在变化之中找规律,在规律之中见关联,去除遮蔽,让学生思维能够充分地从一个点到另一点进行连续的活动.
4 板书优化 结构图表建关联
“关联”如何显性化、可视化,让学生易于学习、接受?——板书!好的板书能对“关联”起到画龙点睛、锦上添花的作用.例如,本节课的板书设计如图9.
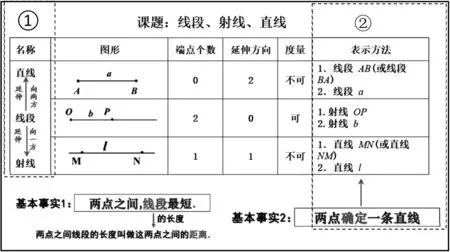
图9
“连线成面”,用最简洁的文字、符号、图案、表格等形式提纲挈领地呈现本节课的核心内容,主次分明、层次清楚.区域①呈现了三个图形之间的关联,区域②呈现了“表示方法”和“基本事实2”之间的关联,而这个表格整体系统地呈现“三线”的区别和联系.如此,学生所学习的知识是成串、立体的,是简约、多触点的,是结构化的.
5 知识内化 方法素养孕关联
“勾面成体”,知识、方法和价值应该呈现一定的层次结构,应该从知识的关联处寻找方法,在方法的通性、本质处寻找价值,这样的关联“应该是构成这样一种含有种种力量——简约化知识的力量,产生新的诊断的力量,使知识体形成愈益严密的体系的力量——的知识系统”[7](布鲁纳语).
例如,在课堂小结时,出示如下问题:
(1)说一说本节课中学习了哪些知识?
(2)理一理“线段、射线和直线”的研究思路;
(3)悟一悟:如果给你新图形——“角”,你准备如何进行研究?
前两个问题不仅回顾了本节课的知识,也帮助学生理顺了图形的研究思路(定义—表示方法—性质);问题(3)不仅做到了前有铺垫、后有延伸,更为学生展示了线与角之间的关联.
这样的课堂小结,舍弃了使人发生混乱的杂乱的枝蔓,突出基本结构.它比具体的数学知识、数学方法的总结具有更高的抽象性和概括性,不是局限于某个知识、某种方法、某类问题,而是站在一定高度,使之更有迁移性和发展性,也更易提升学生的数学学习力,发展学生数学核心素养.
总之,碎片化、点状的数学教学状态呼唤“关联”.关联就是置知识于系统中,着眼于事物之间的联系.“连点成线”“连线成面”“勾面成体”,“点”“线”“面”结合,才能直抵数学知识的内核,构建前后一致、逻辑连贯、一以贯之的学习过程,打造立体课堂,彰显数学教学的活力.

