一节意外生成的数学课
崔豪东 (江苏省南京市溧水区第一初级中学 211200)
课堂是一个动态生成的过程,无论教师课前准备多充分,预设多完美,课堂也未必会按照预设的教学环节进行.课堂常常会和“意外”邂逅,面对“意外”,教师要开启教育智慧,发现这些“意外”的价值,挖掘其背后的教学资源,让“意外”在课堂“开花”.
1 “精心”的预设
在学完苏科版初中数学七年级上册“2.4绝对值和相反数”后,学生对绝对值的概念及其性质有了初步认识,但学生对绝对值的认识还只是局限在代数运算层面,并不能从绝对值的概念中领悟绝对值的深层内涵,对绝对值的认识还未上升到绝对值几何意义的高度.于是,笔者准备上一节绝对值的几何意义专题课,旨在提升学生对绝对值的距离内涵的深层认识.课前,笔者作了充分的准备,设计好教学环节,选好典型例题和针对练习,用心制作PPT课件,悉心编制课堂学习单.笔者预设的课堂教学分三个环节:概念学习,典例精析,巩固练习.
2 短暂的“顺利”
课上第一环节是概念学习,笔者提出了以下三个问题:
问题1:|-2|,|5-0|和|-3-0|分别表示数轴上哪两个点之间的距离?
问题2:|4-2|和|-3-(-2)|分别表示数轴上哪两个点之间的距离?
问题3:|a-b|表示数轴上哪两个点之间的距离?(绝对值的几何意义)
学生通过自主思考和合作交流得出|a-b|指的是数轴上表示a的点与表示b的点之间的距离,掌握了绝对值的几何意义.
课上第二环节,笔者出示例1:利用绝对值的几何意义,求|x-1|+|x-3|的最小值.
题目出示后,学生迅速拿起笔进入思考状态.最先举手的是生1,笔者让她来讲台上展示自己的结果,她一边画图一边说道:“我画了数轴,在数轴上标出表示1和3的两个点,分别记为A和B,把表示x的点记为P.当点P在A,B两点之间时,|x-1|+ |x-3|=PA+PB=AB=2;当点P在点A左侧时,|x-3|=PB>2,|x-1|+|x-3|>2;当点P在点B右侧时,|x-1|=PA>2,|x-1|+|x-3|>2.所以|x-1|+|x-3|的最小值是2.”她的思路很清晰,表达也非常准确.她的话音刚落,黑板上已经呈现出图1.
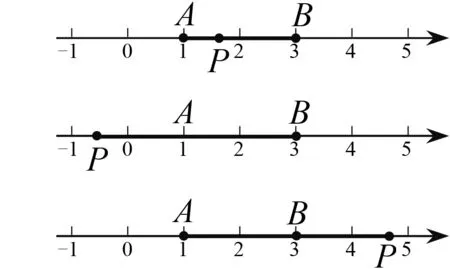
图1
学生们对生1投以赞许的目光,当她走下讲台时,笔者发现有学生默许地点点头,还有学生忍不住感叹道“哦”“我会了”“原来如此”……
3 突来的“意外”
课堂看似很顺利,一直按照笔者的预设进行着.在绝大多数学生理解了例1后,笔者准备出示例2,突然,“意外”发生了.一个声音出现了,这声音来自生2,他说:“老师,当点P在A,B两点之间时,|x-2|的最小值是0,在x=2时|x-2|=0.所以说|x-1|+ |x-2|+|x-3|有最小值,最小值是0+2=2,在x=2时有最小值.”生2的话赢得了全班的一致赞同.笔者对课堂上出现这样的回答有些震惊,看来笔者的课前预设太粗浅.
但这场“意外”为绝对值几何意义的深层学习提供了很好的契机.好吧,那我们就来个“深入虎穴”,把“意外”之效放大、变强!“要是4个绝对值、5个绝对值的和呢?是不是也有最小值呢?”笔者问道.
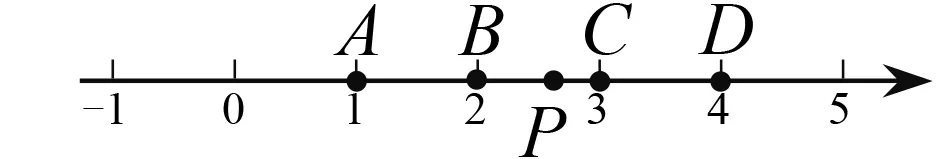
图2
x
P
然后生3接着说:“当点P在A,D两点之间时 |x-1|+|x-4|有最小值3,当点P在B,C两点之间时|x-2|+|x-3|有最小值是1,所以|x-1|+ |x-2|+|x-3|+|x-4|有最小值,最小值是 1+3=4,在x介于2和3之间时有最小值.”
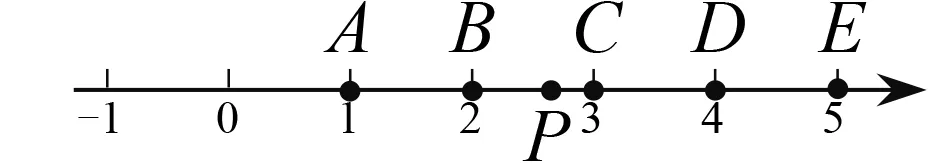
图3
生4继续说道:“以|x-1|+|x-2|+|x-3|+ |x-4|+|x-5|为例,在数轴上依次标出表示1,2,3,4,5的点,分别记为A,B,C,D,E,把表示x的点记为P.当点P在A,E两点之间时|x-1|+ |x-5|有最小值4,当点P在B,D两点之间时 |x-2|+|x-4|有最小值是2,当点P在C处也就是x=3时|x-3|有最小值0.所以|x-1|+ |x-2|+|x-3|+|x-4|+|x-5|的最小值是0+2+4=6.”
“好像有规律”,有学生似乎发现了什么.
“要是99个绝对值、100个绝对值的和呢?是不是也有最小值呢?”笔者继续把“意外”之效推向深入.
“如果有99个绝对值相加,那么它们的和也是有最小值的.以|x-1|+|x-2|+…+|x-99|为例,在数轴上依次标出表示1,2,3,…,99的点,99是一个奇数,最中间的点是表示50的点,当x=50时,|x-1|+|x-2|+…+|x-99|取得最小值”,一向不爱说话的生5居然开口了,而且从言语之中能够感受到他的自信.
“如果有100个绝对值相加呢?|x-1|+ |x-2|+…+|x-100|有最小值吗?”又有学生提出疑问.
“有最小值.在数轴上依次标出表示1,2,3,…,100的点,100是一个偶数,最中间的两个点是表示50和51的点,当x介于50和51之间时,|x-1|+ |x-2|+…+|x-100|取得最小值”,坐在最后一排的生6竟有此感悟.
“求几个绝对值的和的最小值,如果有奇数个绝对值,那么当x取正中间的数值时,绝对值的和最小;如果有偶数个绝对值,那么当x介于正中间两个数之间(含这两个数)时,绝对值的和最小.”学生们经过讨论得出了一致结论.
看到孩子们的集体成果,笔者虽然非常意外,因为这完全超出了预设,但是内心深处却是非常喜悦.
4 深刻的“教训”
课后,笔者回顾这次“意外”课堂的整个过程,并进行深深的反思.虽然没有完成课前预设的教学内容,例2没有来得及讲,更没有针对性练习,上了一节结构不完整的课,但换个角度思考,这节课巧借“意外”,使课堂乘着“意外”之风破浪前行.
当课堂和“意外”邂逅,教师要借“意外”之契机,将课堂推向深入,让“意外”在课堂“开花”.这是这次“意外”课堂给笔者带来的深刻“教训”.

