基于深度学习的短时交通流预测

李 莹,李晓霞

(1.西安邮电大学 现代邮政学院，陕西 西安 710061，2.长安大学 汽车学院，陕西 西安 710061)

1 概述

智能运输系统(ITS)代表了运输系统未来的发展方向，旨在提供更好更智能的服务。主要基于数据采集技术、通信技术和数据库管理技术，可提供包括智能交通控制系统、车祸管理系统、智能交通导航系统、驾驶辅助系统等在内的多个重要应用[1]。

ITS中最重要的便是数据的采集和分析，并在此基础上做出决策。由此可见，ITS天然地与大数据紧密结合在一起。文献[2]和文献[3]指出，精确有效的大数据分析工具能更好地支撑ITS。

虽然对交通流进行精准预测是智能运输系统中的重要组成部分，但是，随着海量数据的积累，传统的分析手段不足以充分挖掘有效信息[4]。文献[5]指出，交通流预测手段已经从传统的基于统计学的参数方法[6]、基于机器学习的非参数方法[7]，演变为基于大数据的深度学习方法[8]。

近年来，文献研究的预测模型主要包括：时间序列模型、神经网络模型、支持向量机模型、历史平均模型等，但是大部分模型未考虑目标路段所在路网的物理空间信息，而是只利用了该路段的历史交通流数据信息。WU[9]等人利用卷积神经网络和循环神经网络分别处理时间、时间维度的信息进行了短时交通流的预测，邹东[10]等人基于Elman神经网络算法构建了预测模型，刘小明[11]等人基于时延特性进行了多断面的短时交通流预测，陆文琦[5]等人基于混合深度学习，构建了智能网联环境下的交通流预测模型，结果表明该模型在不同车道均有理想的预测效果。于德新[12]等人利用GRU-RUN模型对交叉路口的短时交通流进行了预测研究。戢晓峰[13]等人针对节假日的交通流实际数据，建立了基于深度学习的框架进行预测。由此可见，运用神经网络或深度神经网络来开展交通流数据的精准预测是方法发展的趋势，值得进一步深入研究。

然而，大部分研究只开展了单一路段的预测，传统的机器学习模型也很难捕捉到时空特性强烈耦合的道路交通状况的特征，因此交通状态预测的有效性和精度也将受此影响。特别是，当前道路复杂度高、交通数据类型多维、数据量巨大，传统的算法如支持向量机等很难对数据特征进行充分的学习，因此，本文在智能运输系统的背景下，在考虑了多维时空因素的基础上，提出将深度学习架构的SDAE模型用于交通流预测，通过对不同类预测模型对比，验证了模型的有效性和优越性。

2 自编码器和栈式降噪自编码器模型(SDAE)

对智能运输系统(ITS)中产生的海量数据，进行有效的学习利用，从而完成交通流的预测。需要同时考虑训练模型特征提取的充分完备性和预测功能的泛化性，是一项十分艰巨的任务。

2.1 自编码器(AE)

自编码器的基本结构包括输入层、隐藏层和重构层，如图1所示。自编码器的本质是重构输入数据的神经网络，从而获取有效的学习特征、去除数据噪声、提高模型的泛化能力，最终学习到的有效特征被记录于隐藏层。

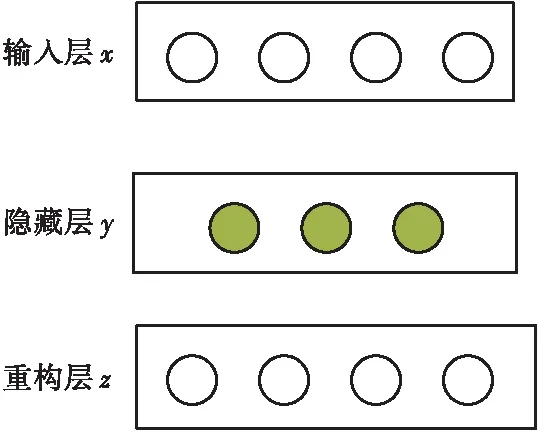
图1 自编码器结构

训练样本集表示为：{x(1),x(2),x(2),…}，x(i)∈Rd,自编码器首先按式(1)将样本x(i)编码，完成了从输入层到隐藏层的映射。进一步按式(2)对y(x(i))进行解码，从而完成隐藏层到重构层的映射。

y(x)=f(W1x+b)

(1)

z(x)=g[W2y(x)+c]

(2)

式中:W1为编码权重矩阵;b为编码偏置向量,W2为解码权重矩阵;c为解码偏置向量，本文默认激活函数f(x)和g(x)为logistic sigmoid函数1/[1+exp(-x)]。

为达到训练效果，使得重构误差最小化，定义损失函数为重构误差LAE:

(3)

进一步可对AE进行无监督训练，利用误差反向传播过程可对网络进行Fine-tuning调优。

2.2 SDAE模型

先在AE的基础上介绍降噪自编码器DAE模型。DAE模型具有与AE一致的网络结构和训练目标，不同之处在于，DAE在训练前主动在样本中添加一定的随机噪声数据，训练过程旨在消除噪声干扰，并重构未污染的纯净输入信息，从而间接地实现抑制噪声数据的效果。文献[14]指出，通过对污染数据的特征映射解析还原原始纯净数据，此过程加强了系统的稳定性和鲁棒性。

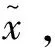
同理，定义损失函数为：

(4)

在DAE的基础上，将l个DAE模型堆叠(Stacked)之后组成深度学习结构，构成SDAE架构，如图2所示。前一层DAE中的隐藏层作为下一层DAE的输入，即可逐层完成训练(共l层)，通过反向误差传播过程进行调优。注意到损失函数保持不变，仍为LDAE，调优标准即为最小化LDAE。

图2 SDAE结构

借鉴文献[8]，为了将SDAE模型用于交通流的预测，需要在最顶层添加一个标准的预测器(Predictor)。本文选择Logistic回归预测器作为深度学习网络的有监督交通流预测器。综上，深度学习网络结构如图3所示，其算法实现过程如表1所示。

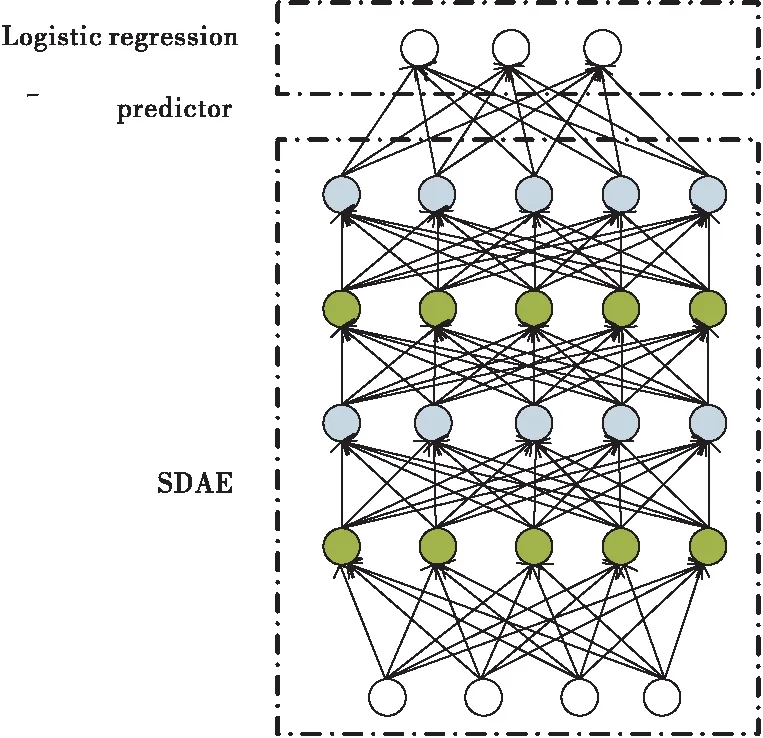
图3 交通流预测的深度学习网络结构

表1 SDAE训练算法Table1 TrainingofSDAE算法1SDAE模型的训练Step1)初始化SDAE网络参数设定网络的学习率α,训练周期κ,网络结构层数l,权重衰减参数λ,初始化编码权重矩阵W1,编码偏置向量b,解码权重矩阵W2,解码偏置向量c,输入层和隐藏层单元数目,对x进行归一化处理后加入噪声:x→x～Step2)训练第一层DAE模型,将其隐含层作为第二层DAE模型的输入,以此类推,直至完成第l层DAE的训练Step3)将n个DAE堆叠形成SDAE,在顶层添加logistic标准预测器实现交通流预测功能Step4)利用BP方法调整整个网络的参数,即对整个网络进行调优

3 数据来源与分析

本文所用数据来源于美国加利福尼亚运输部性能测量系统(PEMS)。该系统由超过15 000个独立探测器对高速公路通过的车辆信息进行采集，采集的时间间隔为5 min。选择2020年10月到11月的数据进行实验，其中80%的数据用于训练，20%的数据用于测试。

根据PEMS指导手册，当且仅当访问对象为独立探测器级别时可获取该道路的交通流信息。对不同道路的探测器数据进行分析，可获取不同道路的交通流时间序列数据。文献[8]将PEMS中所有道路数据作为数据输入算法，从而达到多维时空(Spatial and Temporal)分析的目的。但本文认为，不同道路之间物理距离越远，其空间关联程度越微弱。更合理的做法应该是针对某预测道路对象，将与之相连接的相邻道路数据纳入算法进行分析。

定义所预测路段为AB，记与点A相连的路段共SA条，分别为{lane1,lane2,…,laneSA}，同理点B相连的路段{lane1,lane2,…,laneSB}。

以加州奥克兰市的高速公路为例，如图3所示。选取589号和980号高速公路之间的路段作为预测路段，标记为AB，如图4所示。与点A相连的路段有24号和580号左右两侧高速公路，共3段：{lane1,lane2,lane3}，与点B相连的路段880号和980号高速公路，共两段：{lane1,lane2}。

图4 奥克兰市高速公路布局

图5 预测路段与周边道路结构

AB路段从2020年10月1日到2020年10月4日的交通流量变化情况如图6所示，其趋势表现出明显的一致性。

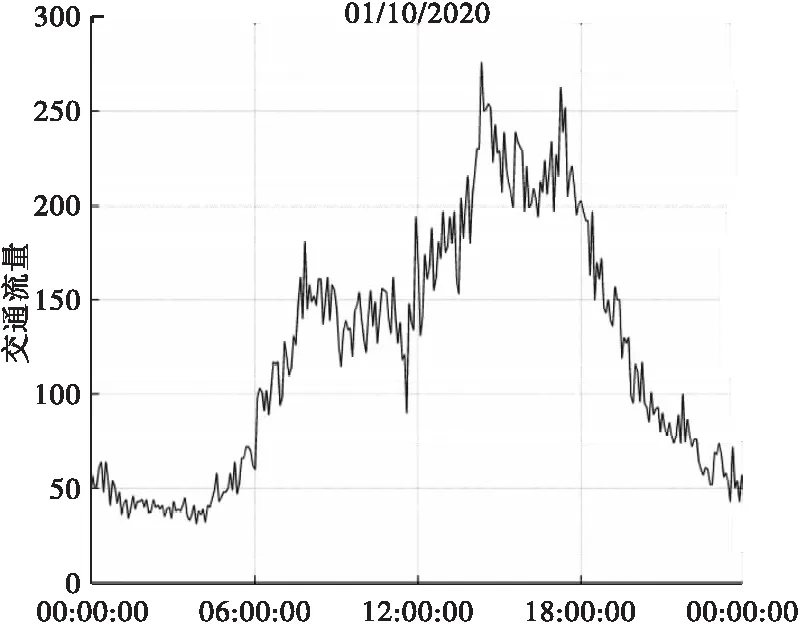
(a)2020年10月1日

4 SDAE模型的预测与对比分析

为了验证模型的有效性和可行性，用以下性能指标进行对比分析：平均绝对误差MAE、平均相对误差MRE和均方根误差RMSE。

为了对预测效果进行对比，选择了基于统计学的时间序列模型ARIMA、基于机器学习的支持向量机模型SVM与本文模型进行对比。特别地，作为纵向对比，还对SDAE模型进行了只输入预测路段时间序列数据的预测训练，将其标记为SDAE-T。作为区分，本文提出的考虑多维时空因素的SDAE则标记为SDAE-ST。

根据SDAE模型的网络结构，需要确定输入层、隐藏层的单元数和隐藏层数目。以AB路段为例，输入数据为AB段交通流的时间序列和相连道路交通流的时间序列，共6组时间序列的数据作为输入。这样处理既能考虑交通流的空间关联性，又能使得训练数据高效简洁。为了预测时刻的交通流量，需要用到前r个时间栈数据进行训练，即Xt-1,Xt-2,…,Xt-r，最终输入数据的维度为6×r，由SDAE的网络结构可知输出层的维度为6。

短期交通流预测，可根据选定的数据天数d确定r：r=288×d。不失一般性，本文设定天数范围为{1,2,…,7}，隐藏层数目l范围{1,2,…,7}，隐藏层单元数目范围为{200,250,300,350,400,450,500,550,600}，运行算法得到最优网络结构如表2所示。

表2 SDAE模型结构Table2 StructureofSDAE结构参数计算结果r864l4隐藏层单元数目[350350350350]

图7和图8分别为2020年11月28日至30日和2020年11月18日至20日的预测效果与观测值的对比。短期交通流预测天数一般不宜过多，存在一定的主观性。本文经多次实验，初步确定天数取d=2较为合适，模型效果较好。

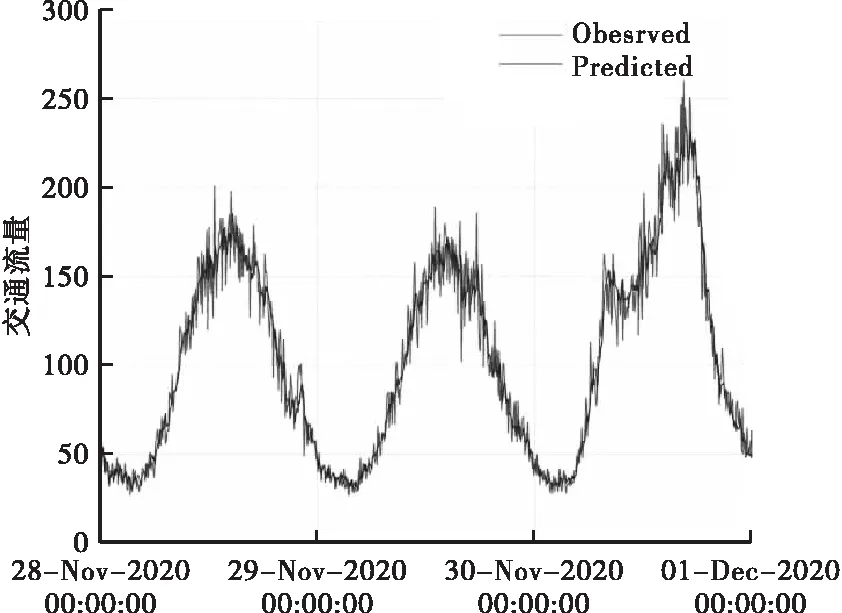
图7 预测效果(11月28日至30日)

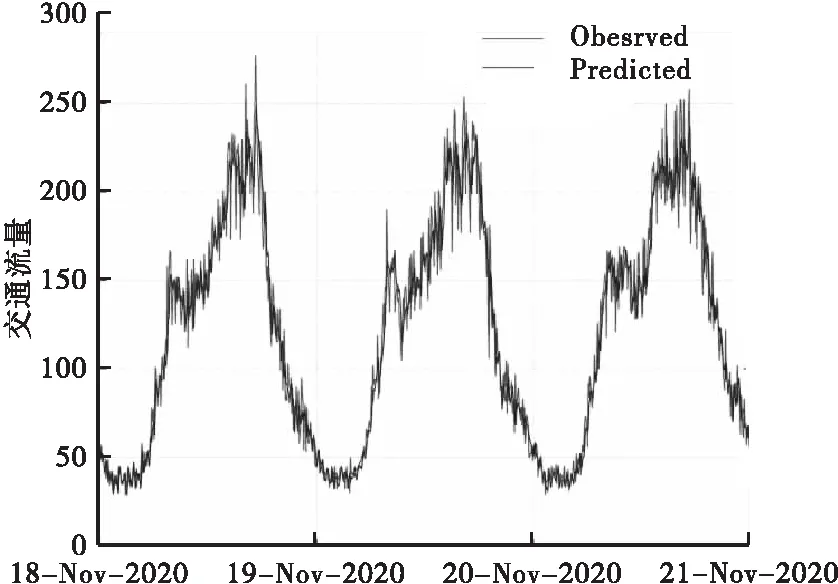
图8 预测效果(11月18日至20日)

预测的结果虽然存在一定的偏差扰动，但所预测的交通流量变化趋势同观测值保持着高度的一致性。

不同模型的预测性能对比情况如表3所示。从表3可知，SDAE-ST的平均绝对误差MAE最小，具有更高的预测精度。而SDAE-T预测精度最低，ARIMA相比更高，SVM则表现为比ARIMA更高的精度，但二者相差不大，属同一预测精度水平。这证明了由于SDAE-T只利用了预测道路的历史数据，而未考虑其路网空间维度的影响，因此预测精度较低。模型之间的平均相对误差MRE和均方根误差RMSE的差异与MAE保持一致，也验证了本文模型的优越性。

综合来看，ARIMA和SVM皆考虑了时空因素的影响，各项指标相差较小，但都高于SDAE-T的预测精度，这说明开展多维时空分析是很有必要的。在所选的几种模型中，SDAE-ST的精度最高，具有更加优越的性能。

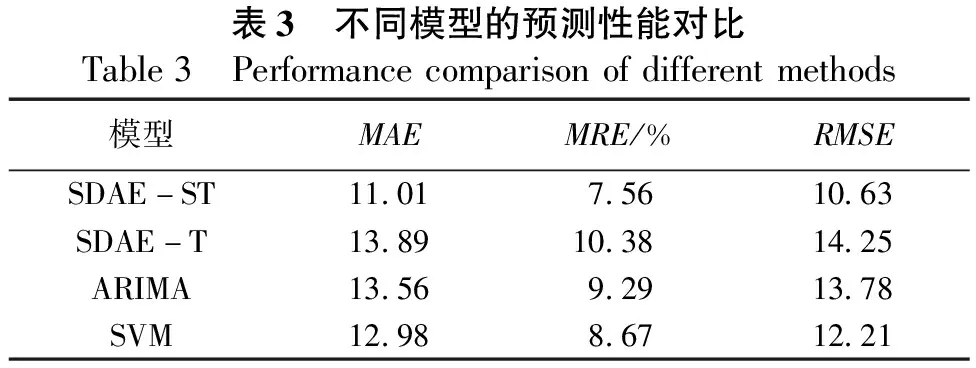
表3 不同模型的预测性能对比Table3 Performancecomparisonofdifferentmethods模型MAEMRE/%RMSESDAE-ST11.017.5610.63SDAE-T13.8910.3814.25ARIMA13.569.2913.78SVM12.988.6712.21

5 结论

智能运输系统环境下，大数据的采集和分析手段更加先进，且交通流预测作为其关键性技术功能，本文得以在大数据的基础上，提出了基于深度学习的交通流预测模型。

模型利用将多个降噪自编码器DAE堆叠的思路，构建了栈式SDAE的深度学习结构，通过在顶层添加Logistic回归预测的设计实现交通流的预测功能。同时结合实际的交通流数据，通过与不同模型的预测实验对比，证明了本方法的有效性。在进行实际交通流的预测时，应考虑多维时空因素的影响，才能获得更好的预测精度。此外，本文数据来源于美国。因此本模型在用于中国高速公路时，需要考虑以下两点。①需要考虑中美两国测量系统的差异、流量计算公式，确保数据的真实。②总的来说中国的交通流量大于美国，因此可以适当放宽时间间隔以应对数据容量的计算压力。