降雨诱发含碎石夹层土坡破坏演化规律研究

肖景红,王 敏,王 川,冷先伦

(1.中交二航局第四工程有限公司，安徽 芜湖 241000；2.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071；3.中国科学院大学，北京 100049)

1 概述

在各种地质作用下，自然界中出现了较多含夹层的边坡；根据夹层与周围岩土体的强度和刚度的关系，这些边坡可分为含软弱夹层的边坡和含硬夹层的边坡[1-2]。这些边坡因受夹层控制，在降雨、地震、地下水、开挖扰动、加载、库水侵蚀等作用下，容易诱发沿夹层滑动并最终形成滑坡[3-4]。当前，含夹层的边坡破坏已经成为边坡工程研究的热点之一，国内外学者就其中含软弱夹层的一类边坡开展了大量研究，认为：软弱夹层作为一种层状的结构层存在于边坡内，其强度、刚度及几何尺寸相对周围岩土体较小，特别是在降雨入渗、地震、开挖卸荷的过程中，软弱夹层的强度和刚度均急剧降低，成为边坡变形与稳定性控制的短板，并针对这一短板提出了相对应的支护体系[5-6]。然而，当前研究以含软弱夹层的岩质边坡为主，对于含碎石夹层等坚硬、强透水夹层的土质边坡研究较少。

在山谷、河谷等地区，在过去某一时期水力搬运的作用下，形成了碎石夹层等堆积层(洪积层)，继而在后期地质作用或滑坡等地质灾害的影响下，地表倾斜形成含碎石夹层的边坡[7-8]。尽管含碎石夹层的土坡在几何上与含软弱层的岩坡相似，研究方法在一定程度上可以相互借鉴，然而，由于碎石夹层在土坡中并非以软弱夹层的形式存在，相反地，碎石夹层本质上是一种土石混合体，已有研究[9-10]证明，土石混合体的强度大于纯土体的强度，因此碎石夹层在土坡中属于硬夹层。碎石夹层在土坡中的力学特性及其与周围土体的相互作用机理必定与岩坡中的软弱夹层具有较大的差异，因此含碎石夹层的土坡需要单独研究。

鉴于当前对含碎石夹层土坡的稳定性研究较少，在降雨作用下碎石夹层所形成的优势渗透面对边坡稳定性的影响认识不充分，相关数值计算方法较为缺乏，本文开展了降雨诱发含碎石夹层土坡破坏演化规律的研究。首先概化了含碎石夹层土坡的几何模型并构造了极限平衡法受力分析模型，分析了雨水沿碎石夹层入渗形成的优势渗透面对边坡稳定性的影响机制；其次基于Janbu法推导了考虑优势渗透面效应的极限平衡法公式，实现了含碎石夹层土坡降雨入渗的极限平衡法数值计算；最后基于广西某公路边坡的破坏案例分析了降雨诱发含碎石夹层土坡破坏演化规律。研究成果可为降雨作用下含碎石夹层土坡的变形与滑坡控制提供参考。

2 降雨诱发含碎石夹层土坡破坏的力学模型

2.1 简化模型与假设

土坡中碎石夹层的厚度和层面形态通常具有一定的空间变异性，即在不同的空间位置上，碎石夹层具有不同的厚度和不同的表面形态。为了简化分析，在此不考虑碎石夹层的这种空间变异性，即将碎石夹层看作在空间上等厚度的夹层且夹层的表面形态为平面，见图1。根据坡角α与碎石夹层倾角β的关系，将含碎石夹层的土坡分为以下3种类型，即：α>β[类型I，见图1(a)]、α<β[类型II，见图1(b)]和90°<β<180°[类型III，见图1(c)]。碎石夹层作为土坡内部的大型结构面，对于边坡稳定性影响较大，其中以类型I和类型II(均为顺倾向)方式赋存的夹层为甚，因此本文对含类型I和类型II碎石夹层土坡的稳定性规律进行深入研究。

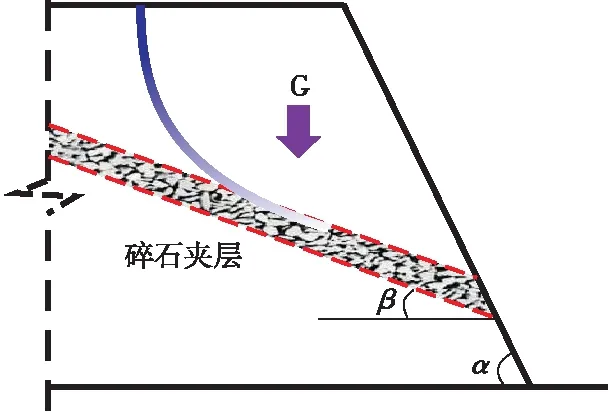
(a)类型I

碎石夹层本质上是一种土石混合体，一般而言，与组成土石混合体的黏土相比，土石混合体的渗透性显著高于黏土的渗透性[11-12]。因此，在含碎石夹层的土坡中，假定：碎石夹层渗透性显著高于周围土体，降雨过程中雨水易汇入碎石夹层并沿碎石夹层形成优势渗透面，雨水沿优势渗透面快速下渗，在边坡内部看作雨水仅沿碎石夹层渗流，而不会造成碎石夹层周围土体饱和度变化。基于此，建立沿碎石夹层优势渗透面的土坡稳定性计算模型，见图2。

(a)边坡简化模型

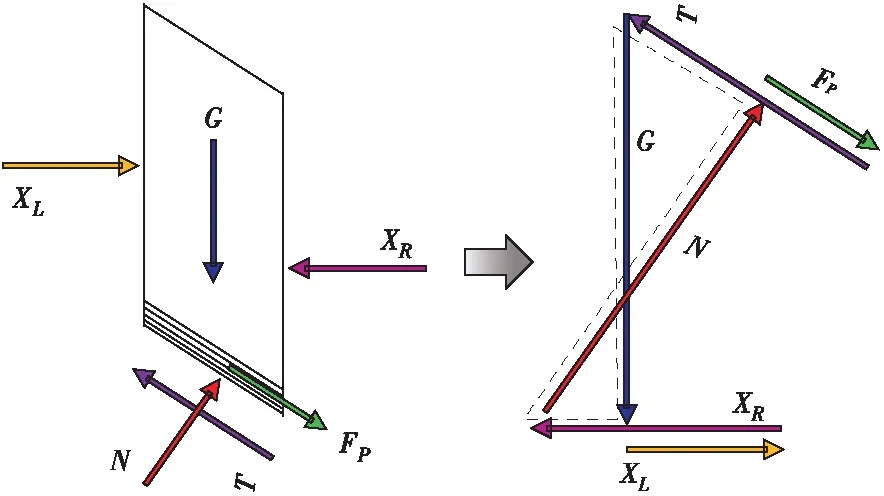
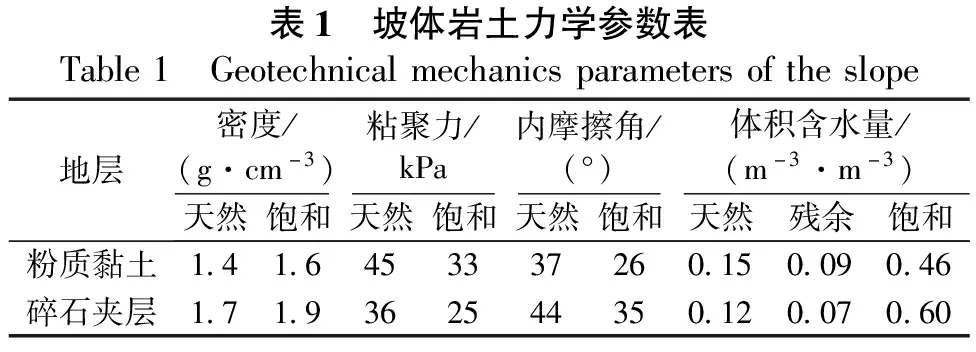
降雨入渗过程中，坡顶碎石夹层出露位置最先饱和，随着雨水沿着碎石夹层持续入渗，边坡上部的碎石夹层逐渐饱和，形成饱和段(长度为hs)，边坡下部的碎石夹层由于雨水入渗的延迟和损失，处于非饱和状态[长度为(1-h)s]，见图2(a)。其中，s为碎石夹层长度，h为某时刻碎石夹层饱和段占全段长度的比值，定义为碎石夹层的饱和比。从图2(a)中取出一个单元体进行受力分析，见图2(b)：Δs为单元体底部滑动面的长度，β为碎石夹层与水平面的夹角，H为坡面到碎石夹层底部的深度，mH为碎石夹层的厚度(0

2.2 刚体极限平衡稳定性分析

Janbu法是一种成熟的、多国规范采用的考虑结构面效应时边坡稳定性分析的一种方法，该方法最大限度地满足了各个单元体受力的平衡(未考虑单元体整体的力矩平衡)，是一种适用于由结构面控制的非圆弧滑动面的边坡稳定性分析的极限平衡法[13]。本文在Janbu法推导安全系数方法的基础上，考虑了雨水沿碎石夹层入渗形成的优势渗流面效应及碎石夹层非饱和抗剪强度效应，扩展了Janbu法的应用场景。单元体受力和力矢量多边形如图3所示。

图3 基于Janbu法的单元体受力分析示意图

2.2.1下滑力

下滑力由单元体沿碎石夹层方向的重力分量FL和单元体内雨水沿碎石夹层向下渗流的渗透力FP两部分组成，根据图2(b)和图3中所示的几何关系，FL和FP分别为：

FL=G·sinβ

(1)

FP=γwmΔs·sinβ·cosβ

(2)

式中:γw为水的重度。单元体的重力G由碎石夹层和上部土体组成，即:

G=ΘγHΔs·cosβ

(3)

其中，

Θ=m(n-1)+g(1-n)+nS(1-m)

(4)

式中:n为土体孔隙率；g为土粒比重；S为降雨过程中碎石夹层某时刻的饱和度，表达式为：

(5)

式中:θr、θs和θ分别为碎石夹层残余含水率、饱和含水率和某时刻的含水率。

2.2.2抗滑力

碎石夹层作为优势渗透面，降雨入渗下其含水量、孔隙水压力等水力特征变化较大，抗剪强度也随之发生较大变化。碎石夹层的抗滑力由饱和段抗剪强度τ1和非饱和段抗剪强度τ2共同确定，其中饱和段满足Mohr-Coulomb准则，即:

τ1=c′+(σn-uw)tanφ

(6)

非饱和段满足Fredlund双变量非饱和抗剪强度准则[14]，即:

τ2=c′+(σn-ua)tanφ+cφ

(7)

式中:(σn-ua)为法向净应力；σn为法向总应力；uw和ua分别为孔隙水压力和孔隙气压力;c′为饱和碎石夹层有效粘聚力;cφ为非饱和碎石夹层基质吸力贡献的粘聚力;φ为碎石夹层有效内摩擦角。

一般情况下，基质吸力范围变化很大，直接确定基质吸力与抗剪强度间关系很困难，本文参照SCHILIRO[15等对残积成因的砂土和黏土(与本文分析的含碎石夹层的土坡成因相似)进行的试验研究结果，确定饱和度S与cφ之间的关系为：

cφ=(1-S)λ

(8)

式中:λ为拟合参数，对于软土、硬黏土、中砂和粗砂等土体，λ=0.4。

此时可将碎石夹层非饱和段和饱和段的黏聚力进行均一化处理，即转化为具有等效表观黏结力∑C的均一碎石夹层，即:

∑C=[c′+(1-h)(1-S)λ]s

(9)

均一化后的碎石夹层抗滑力∑T仍然满足Mohr-Coulomb准则，即:

∑T=∑(Gcosβ·tanφ)+∑C

(10)

将式(3)和式(4)代入式(10)，可得:

∑T=∑(ΘHγtanφ·cos2α)+∑C

(11)

2.2.3边坡安全系数

联立式(1)、式(2)和式(11)可求得含碎石夹层的不同单元体的稳定系数η为：

(12)

由此可得碎石夹层段边坡安全系数为：

(13)

3 边坡实例研究

3.1 依托工程介绍

在建的天峨至北海公路(天峨经凤山至巴马段)途径多处残积土边坡，坡体以粉质黏土为主，部分边坡中含有不同程度的碎石夹层，其中广西河池市天峨县岜暮乡纳基村南面山体边坡(见图4)碎石夹层的分布特征最为突出。该边坡开挖后几何及地质特征如图4(a)所示。2021年3月初该边坡开挖完成，随后经历了近半月的梅雨期，每日降雨量约为10～20 cm。至3月中旬，该边坡突发滑坡，滑体位置见图4(b)，滑坡后缘出现多条宽度约为20 cm的拉裂缝[见图4(c)]，滑体侧翼出现显著的剪切裂缝并出现大量的碎石[见图4(d)]。通过对开挖面附近调查发现，该滑坡处含有碎石夹层，夹层的形态如图4(e)所示。地质勘察揭示坡体岩土力学参数如表1所示。

(a)边坡二维剖面图

通过现场调查，专家认为该滑坡形成的主要原因为：①碎石夹层在滑坡面出露，形成不利地质结构；②边坡开挖后连续降雨，雨水汇入碎石夹层形成优势渗流面，进而雨水沿此优势渗流面渗入边坡内部；③雨水渗入边坡内部后，边坡发生渐进失稳，后缘首先出现贯通拉裂缝，滑体从第一条拉裂缝处沿碎石夹层变形、滑动。为了进一步明确该边坡失稳破坏机理，本文基于Geostudio软件平台中非饱和渗流和极限平衡分析模块，将第二部分提出的含碎石夹层土坡稳定性分析方法通过自定义函数的形式嵌入数值分析中，研究降雨入渗下该边坡的渗流场及潜在滑动面安全系数的变化规律，明确降雨入渗下含碎石夹层边坡的稳定性计算方法。

表1 坡体岩土力学参数表Table1 Geotechnicalmechanicsparametersoftheslope地层密度/(g·cm-3)粘聚力/kPa内摩擦角/(°)体积含水量/(m-3·m-3)天然饱和天然饱和天然饱和天然残余饱和粉质黏土1.41.6453337260.150.090.46碎石夹层1.71.9362544350.120.070.60

3.2 数值分析条件

3.2.1渗流分析条件

非饱和渗流分析需要的土体参数包括土水特征曲线(Soil Water Characteristic Curve，SWCC)和渗透系数曲线(Hydraulic Conductivity Curve，HCC)，由于获取这两条曲线需要的时间成本和资金成本较高，通常情况下根据土体特征采用经验拟合的形式进行确定。本文基于Geostudio软件平台中的经验数据，采用Fredlund和Xing等推导的土水特征函数[11][见式(14)]和渗透特征函数[12][见式(15)]，分别拟合粉质黏土和碎石夹层的土水特征曲线[见图5(a)]和渗透系数曲线[见图5(b)]。

(a)土水特征曲线

(14)

(15)

式中:a、n和m是控制体积水含量函数形状的曲线拟合参数;C(φ)是相关函数;θsat是饱和体积水含量;θres是残余体积水含量;Ksat是饱和渗透率;x是表示含水量的虚拟积分变量。

渗流分析初始边界条件为：根据地质勘察揭露的地下水位，在图4(a)所示的边坡模型底部施加0 m的压力水头作为初始水位线，模型的左侧边界和右侧边界均设置为不透水边界。在降雨入渗分析阶段，由于降雨量为10～20 cm/d，因此在边坡模型顶部粉质黏土上施加10 cm/d的入渗边界，考虑到碎石夹层处雨水易汇集，在模型顶部碎石夹层处施加30 cm/d的入渗边界。降雨入渗分析时长为5 d。

3.2.2边坡稳定性分析条件

由于滑动面非圆弧状，而是由两部分组成的复合滑动面，即沿碎石夹层的直线段和切割粉质黏土的圆弧段组成，滑动面难以实现自动检索，因此采用指定潜在滑动面的方式进行计算，根据开挖平台的分布情况，指定了4个潜在滑动面，见图6。极限平衡法分析在渗流分析的基础上开展：对于饱和段，采用表1中的饱和抗剪强度参数，强度准则参见式(6)；对于非饱和段，采用表1中天然状态下的强度参数，并采用式(7)中的强度准则来考虑到含水率变化的影响；碎石夹层滑动段的整体强度准则通过式(9)确定。滑动面的抗剪强度通过式(11)确定，滑动面的安全系数通过式(13)确定。

图6 边坡潜在滑动面设置

3.3 考虑碎石夹层优势渗透面的土坡稳定性分析

3.3.1碎石夹层优势渗透面分析

碎石夹层的优势渗透面效应体现为：在降雨入渗下，碎石夹层的含水量、孔隙水压力、渗流速率、等渗流评价指标显著高于周围土体。由于这些指标相互关联，因此仅以其中最直观的指标“体积含水量”为代表开展碎石夹层优势渗透面分析，见图7。由图7可知：①降雨入渗前，坡体含水量由下至上逐渐降低，在坡顶处坡体处于残余含水量状态，在坡角处坡体处于自然含水量状态，见图7(a)；对比前人的研究可知，坡体初始含水量分布情况符合边坡自然状态下的含水量分布规律[16]；②降雨入渗1 d后，坡面0.6 m深度范围内的土体基本饱和，在坡顶碎石夹层处由于雨水的汇集，碎石夹层的饱和深度(约为2.0 m)高于坡面土体的饱和深度，碎石夹层的优势渗流面初步形成[见图7(b)]；③降雨入渗3 d后，坡面土体的饱和状态基本维持降雨入渗1 d后的状态[见图7(b)]，坡顶碎石夹层处饱和深度(约为4.5 m)持续增大，同时由于碎石夹层渗透速度较快，部分雨水沿碎石夹层快速下渗，从而使得整个碎石夹层的含水量均有一定增加，此时碎石夹层的优势渗透面完全形成[见图7(c)]；④降雨入渗5 d后，边面土体的饱和状态相对于降雨入渗1 d后基本无变化[见图7(b)]，而碎石夹层的优势渗透面相对于降雨入渗3 d后得到了进一步强化[见图7(d)]。

图7 不同降雨工况下边坡碎石夹层含水量分布图

3.3.2考虑优势渗透面的极限平衡分析

在碎石夹层每一步降雨入渗分析的基础上，采用第2节提出的分析方法，研究边坡降雨入渗的不同阶段各潜在滑动面的安全系数及其演化规律，见图8。由图8可知：①降雨入渗前，边坡不同潜在滑动面中，底部的滑动面安全系数最低，属于该状态下最危险滑动面，见图8(a)；对比前人的研究可知，边坡的这种滑动面安全系数分布情况符合一般均质多级边坡安全系数的分布规律[17]；②降雨入渗1 d后，随着坡顶碎石夹层优势渗透面的初步形成，坡顶碎石夹层处的抗剪强度受到较大影响，致使经过坡顶碎石夹层的所有潜在滑动面的安全系数均受到一定影响，特别地，边坡上部的潜在滑动面所受影响较大，此时边坡的最危险滑动面为边坡中部二级台阶处的滑动面(滑动面2)，见图8(b)；③降雨入渗3 d后，随着碎石夹层优势渗透面的完全形成及碎石夹层饱和段的向下延伸，边坡各潜在滑动面的安全系数均进一步降低，且最危险滑动面不断向下发展，此时边坡最危险滑动面为边坡中下部三级台阶处的滑动面(滑动面3)，见图8(c)；④降雨入渗5 d后，边坡中下部潜在滑动面的安全系数进一步降低，边坡中上部的安全系数已降至最低，边坡最危险滑动面已向下发展至坡角处(滑动面4)，见图8(d)。

(a)无降雨

3.3.3优势渗透面的发展与边坡稳定性演化规律

为了将边坡碎石夹层优势渗透面的发展过程与边坡的稳定性演化规律联系起来，绘制了边坡降雨入渗下碎石夹层的受影响深度与边坡各潜在滑动面安全系数变化规律的关联图，见图9。随着降雨持时的增加，雨水沿碎石夹层的下渗深度逐渐增加：①各潜在滑动面的安全系数整体上呈现出逐渐降低的趋势；降雨持时达到一定时间后，边坡上部的潜在滑动面安全系数降至最低，随后安全系数不再变化，例如滑动面1在降雨持时达到2 d后安全系数不再变化，滑动面2降雨持时达到3 d后安全系数不再变化；②无降雨情况下，边坡最危险滑动面为经过坡角的滑动面(滑动面4)，降雨入渗改变了边坡最危险滑动面的空间位置：降雨沿碎石夹层入渗的初始阶段，边坡上部滑动面受降雨入渗影响较大，边坡最危险滑动面为边坡上部的滑动面(滑动面1或滑动面2)；随着降雨入渗的持续，边坡最危险滑动面不断向下发展，降雨持续3 d后，边坡最危险滑动面发展至边坡中下部(滑动面3)；降雨持续5 d后，边坡最危险滑动面发展至坡角(滑动面4)；③上述分析的随着降雨持续入渗引发的边坡破坏形态(即随着降雨持续入渗，安全系数小于1的滑动面首次出现在滑动面3处)与依托工程边坡实际破坏形态[即滑动面出现在三级台阶(滑动面3)处]基本一致，从而在一定程度上验证了本文分析的合理性。

图9 雨水下渗深度与边坡潜在滑动面安全系数的变化规律

4 结论

针对含碎石夹层的土坡降雨入渗下边坡稳定性演化规律的研究不足，本文通过分析降雨沿碎石夹层入渗形成的优势渗透面对边坡稳定性的影响机制，基于Janbu法推导了考虑优势渗透面效应的极限平衡数值计算公式，并实现了含碎石夹层土坡降雨入渗下坡体稳定性的工程实例分析。研究表明：

a.对于碎石夹层出露的土质边坡，碎石夹层在降雨入渗下因其强渗透特性和受雨水汇集的影响，容易形成优势渗透面，且优势渗透面效应随着降雨持时的增加而愈加显著。

b.优势渗透面为雨水的下渗提供了快速通道，使得雨水容易渗入边坡内部，造成碎石夹层的抗剪强度急剧降低，边坡安全系数亦随之降低；在边坡安全系数不断下降的同时，边坡最危险滑动面的空间位置由边坡上部不断向下演化，直至最危险滑动面演化至边坡某一位置且安全系数减小至临界值而引发滑坡。

c.通过对工程实例的分析与工程现场的对比研究表明，本文提出的考虑碎石夹层优势渗透面的土坡稳定性分析方法具备一定的合理性，在后续的研究中可将支护结构对含碎石夹层土坡稳定性的作用机理考虑进本文分析方法中。