矩阵Hadamard积特征值估计

李 华

(河南城建学院 数理学院,河南 平顶山 467036)

1 预备知识

记N={

1,2,…,n},Cn×n(Rn×n)表示n阶复(实)矩阵集,设A=(aij)∈Rn×n,σ(A)表示矩阵A的谱集合,ρ(A)表示A的谱半径.若aij≥0(aij>0),则A为非负(正)矩阵,记Zn={

A=(aij)|aij≤0,i≠j

},设A=(aij)∈Zn.若A=sI-B,B>0,s≥ρ(B),则称A为M-矩阵.若s>ρ(B),称A为非奇异M-矩阵,非奇异M-矩阵的集合记为Mn.称

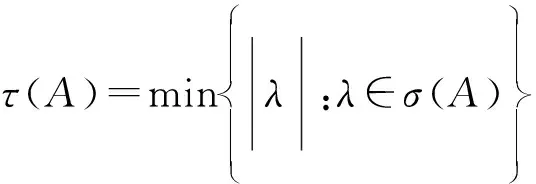
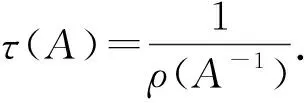
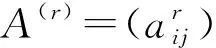
设B=(bij)∈Mn,E=diag(bii)>0，记N=E-B,JB=E-1N,则JB为非负矩阵.

对于非奇异M-矩阵A=(aij)与非奇异M-矩阵B=(bij)的逆矩阵B-1=(βij)的Hadamard积AoB-1的最小特征值的估计有如下结果：

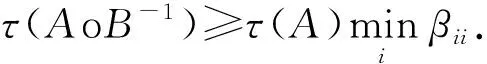
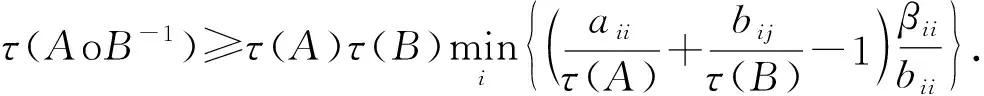
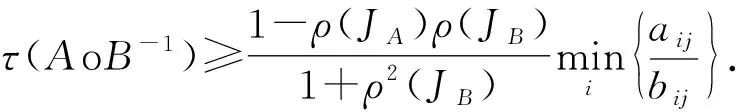
2015年蒋建新[4]得到：

本文首先对非奇异M-矩阵A=(aij)与非奇异M-矩阵B=(bij)的逆矩阵B-1=(βij)的Hadamard积的最小特征值进行估计,得到新的估计式.然后对M-矩阵最小特征值的下界进行估计，得到新的不等式.

2 主要结果

引理 1[3]设B=(bij)∈Mn且不可约，y=(yi)>0,有JBy=ρ(JB)y.则对于B-1=(βij)有：

引理 2[5]设a=(a1,a2,…,an)T≥0,b=(b1,b2,…,bn)T≥0,则有：

其中k=1,2

引理 3[6]设P为非负不可约，若存在不等于零的非负向量z使得Pz≤kz,则ρ(P)≤k.

引理 4[7]设Q∈Mn且不可约，若存在不等于零的非负向量z使得Qz≥kz,则τ(Q)≥k.

定理1 设A=(aij),B=(bij)∈Mn,B-1=(βij),且A和B为不可约矩阵,则有:

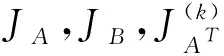
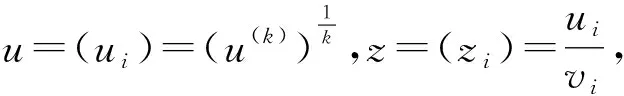
由引理4得：

由于τ(C)=τ(CT)则有：

上式对k=1,2成立.

定理2设A=(aij)≥0,B=(bij)∈Mn,B-1=(βij),且A和B为不可约矩阵,则有

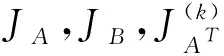
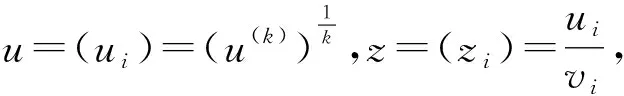
由引理3得：

即：

上式对k=1,2成立.

定理3 设B=(bij)∈Mn,B-1=(βij)，则有

其中k=1,2.

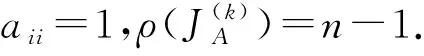
3 数值例子

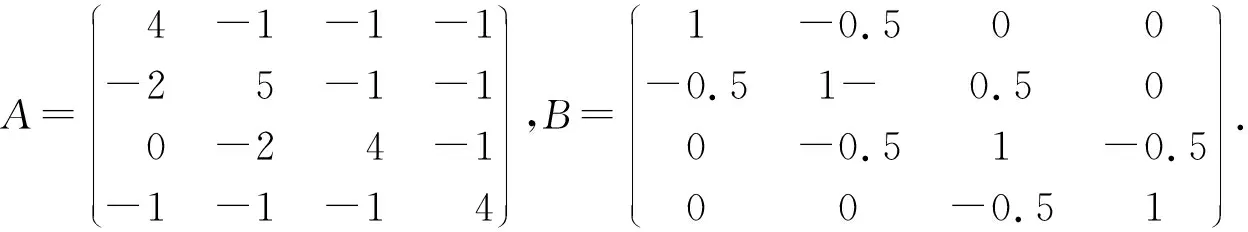
由文献[4] 的结果知：

由文本定理1知,当k=2时,

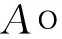
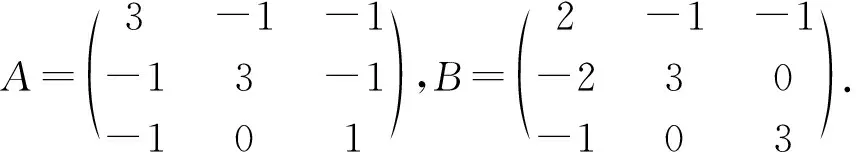
由文献[4] 的结果知：

由文本定理1知,当k=2时,

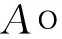
从例1和例2的结果可知,本文定理1的结果在一定条件下比文献[1-4]所得到的界值估计更精确，且易于计算.