印尼某防浪堤地震液化综合判定及影响研究

张 波

(中赟国际工程有限公司，河南 郑州 450000)

饱和砂土受到地震作用时，孔隙水压力骤然上升，在短暂时间内来不及消散，砂粒之间的有效应力完全消失，丧失抗剪强度与承载能力，地基变成像液体一样的状态，称为液化[1]。液化会造成土体侧移和震陷，导致地基失效，影响工程质量和人类生命安全。

印尼地处太平洋地震带，是一个地震多发国家，几乎每年都要发生较大强度的地震，地震烈度一般在7度以上。印尼苏门答腊岛沿海为平原地带，地表遍布新近堆积的砂土。此外，滨海地区地下水普遍较浅，在地震作用下，苏门答腊岛沿海地区地基土存在发生液化的潜势。

目前，对地震诱发土体液化的机理和评价方法的相关研究已经较为充分。土体液化评价方法主要包括统计法与地震反应分析法。统计法以地震现场的液化调查资料和场地勘测资料为基础，建立经验准则和公式，如采用标准贯入锤击数为参量的经验公式，给出判别液化的条件与界限。统计法直观、实用、简单，对影响饱和砂土液化的重要因素可予以考虑，较容易被接受，已列入许多设计规范，如我国的《建筑抗震设计规范》(GB 50011-2010)[2]以及Seed法[3]。长期以来，液化判定方法较多，但不同方法对砂土地层液化潜势评价结果的影响，并无深入探讨，地震液化引起的防浪堤水平侧移和震陷情况时有报道。

本研究以印尼苏门答腊岛沿海地区某防浪堤工程为研究对象，开展原位测试与室内试验，获取土体物理力学参数。基于工程实践中常用的国标法、Seed法、神经网络法与EERC法等统计方法，分别判定砂土的液化潜势，分析液化引起的防浪堤水平侧移与震陷量，用于指导印尼滨海地层液化判定与预防，为海外防浪堤项目类似地层液化评估提供参考。

1 研究场地

研究区位于印尼苏门答腊岛西北部，浅部地层主要为砂土、粉土和黏土，地下水位较高，近地表，其埋深为0 m。现场布置一钻孔，经过现场标贯测试与室内试验，场地典型地层特征参数如表1所示。

表1 研究区地层特征参数

根据《印度尼西亚地震区划图》，工程场地50 a超越概率10%水平(重现周期500 a)的基岩峰值加速度为0.25 g。根据场地实测标准贯入锤击数，依据印尼规范(SNI 03-1726-2002)[4]，地表峰值加速度为0.32 g，对应我国的Ⅷ度区。

某防浪堤采用双堤环抱式布置形式，西防浪堤垂直岸线布置，向东南弯曲，远端延伸至等深线-9.0 m的位置，东防浪堤延伸至等深线-6.0 m的位置，防浪堤总长1 180.19 m。防浪堤结构按允许少量越浪设计，堤心抛填10～600 kg级配良好的开山石，堤心顶宽为7 m，高程为2.0 m，斜坡坡比为1：1.5。针对不同水深和波浪，西防浪堤堤头采用15 t扭工字块摆放两层，东防浪堤堤头采用8 t扭工字块摆放两层。西防浪堤堤身段外侧采用4 t、8 t、10 t与12 t扭工字块摆放两层，护面块体下设块石垫层；堤身段内侧采用4 t扭工字块摆放两层进行防护。东防浪堤堤身段内、外侧均采用4 t、8 t扭工字块摆放两层，护面块体下设块石垫层。防浪堤底采用块石护底，护底长度堤头段为35 m，堤身段外侧为20～25 m，内侧为10～15 m。护岸为实体斜坡式结构，防护范围为-1～+2 m，坡比采用1：1.5，护岸外侧安放800 kg块石两层护面，并设65 cm厚40～80 kg的块石垫层，内侧由上至下分别设置土工布、混合倒滤层及两片石垫层。

2 液化判定

2.1 国标法

我国抗震规范规定，在20 m深度范围内，当饱和砂土、粉土标准贯入锤击数(未经杆长修正)小于或等于液化判别标准贯入锤击数临界值时，应判为液化土，并认为黏土不具液化潜势。液化判别标准贯入锤击数临界值可按式(1)计算：

(1)

式中：Ncr为液化判别标准贯入锤击数临界值；N0为液化判别标准贯入锤击数基准值；ds为饱和土标准贯入点深度(m)；dw为地下水位(m)；ρc为黏粒含量百分率，当小于3%或为砂土时，应采用3%；β为调整系数，设计地震第一组取0.80，第二组取0.95，第三组取1.05。

在探明各液化土层的深度和厚度基础上，按式(2)计算土层的液化指数，并划分相应的液化等级：

(2)

表2 国标法液化判定结果

图1 假定土柱在地震荷载作用下的刚体运动

式中：IlE为液化指数；n为在判别深度范围内每一个钻孔标准贯入试验点的总数；Ni、Ncri分别为i点标准贯入锤击数的实测值和临界值；di为i点所代表的土层厚度(m)；Wi为i土层单位土层厚度的层位影响权函数值(单位为m-1)。

采用国标法计算，钻孔液化判定结果如表2所示，液化深度至15 m，液化指数为12.35，液化等级为中等。

2.2 Seed法

将土体由振动作用产生的循环应力比(CSR)与循环抗力比(CRR)进行比较。如果安全系数FS=CRR/CSR≥1，则判别为不液化，反之，则判别为液化[5]。

(1)CSR计算

如图1所示，假定水平地面下存在一个具有单位宽度和长度的土柱，地面在地震荷载作用下产生最大加速度为amax的水平运动。则作用在土柱上的水平地震荷载F可表示为：

(3)

式中：F为作用在单位宽度和长度的土柱上的水平地震荷载(kN)；m为土柱的总质量(kg)；W为土柱的总重量(kN)；γt为土体的总容重(kN/m3)；z为土柱距地表的深度(m)；a为土柱运动的加速度(m/s2)；σv0为土柱底部的总上覆应力(kPa)。

在水平方向上进行力的合成后，作用在刚体土柱上的荷载F等于其底部的最大剪力，由于土柱具有单位长度和宽度，因此F数值即为最大剪应力τmax。式(3)两边同除以上覆有效应力σv0′，则有：

(4)

由于地震时土层中任一点剪应力的时程变化呈不规则形状，具体应用时需将其用等效的平均剪应力代替，即τcyc=0.65τmax，将其代入式(4)，得到循环应力比为：

(5)

式中：rd为应力折减系数。

(2)CRR计算

循环抗力比反映了在地震荷载作用下土体的抗液化强度，依据标准贯入原位试验进行评价。首先对标贯实测数据按式(6)进行试验方法的修正：

N60=1.67EmCbCrN

(6)

式中：N60为经过试验方法修正后的标准贯入击数；Em为锤击系数(对于安全式落锤为0.60，对于圆锤为0.45)；Cb为钻孔孔径系数(对于65～115 mm孔径为1.00，对于150 mm孔径为1.05，对于200 mm孔径为1.15)；Cr为杆长系数(钻杆杆长小于等于4 m时为0.75，杆长4～6 m时为0.85，杆长6～10 m时为0.95，钻杆杆长大于等于10 m时为1.00)；N为标贯实测数据。

在液化分析时，还需考虑上覆有效应力的影响，进行相应的修正，即：

(N1)60=CNN60=(100/σv0′)0.5N60

(7)

式中：(N1)60为经过试验方法和上覆有效应力修正后的标贯击数；CN为上覆有效应力修正系数，其值一般为1.7～2.0。

根据大量地震时的现场实测数据，包括液化场地和非液化场地，Seed等学者在1985年提出了7.5级地震下标贯击数与CRR的对应关系，此后又根据一系列新的地震实测数据进行了改进[6-7]。采用Seed法计算，钻孔液化判定结果如表3所示，Fs范围为0.59～1.40。Seed法没有液化等级概念，只有是否液化的判定结果。

2.3 神经网络法

由于影响砂土液化的因素很多，而且影响因素与砂土液化势之间呈高度的非线性关系，近年来很多学者采用人工神经网络来建立砂土液化预测模型。神经网络法是一种经验方法，它基于历史资料的经验来预测未来砂土液化事件的发生规律。所以，神经网络模型采用的学习样本必须具有代表性，且有足够的数量。本文采用陈国兴等[8]提出的基于神经网络模型的砂土液化概率判别方法(取国内外25次大地震中344个场地的饱和砂土实测资料作为样本，其中液化场地206个，非液化场地138个)，对钻孔细砂层进行概率判别。根据概率论的基本概念，若样本足够大，则给定抗液化安全系数下饱和砂土液化概率Pl为：

(8)

式中：fl(Fs)和fnl(Fs)分别为经统计分析得出的饱和砂土液化和非液化的概率密度函数。对实测数据的液化概率进行曲线拟合，得出的函数如下：

(9)

为便于工程应用，按液化概率水平将饱和砂土液化势分为三个等级，其建议标准如表4所示[9]。

利用上述模型对钻孔细砂层的液化判别结果如表5所示，Pl范围为0.49～0.91，液化潜势评价为可能液化～液化。

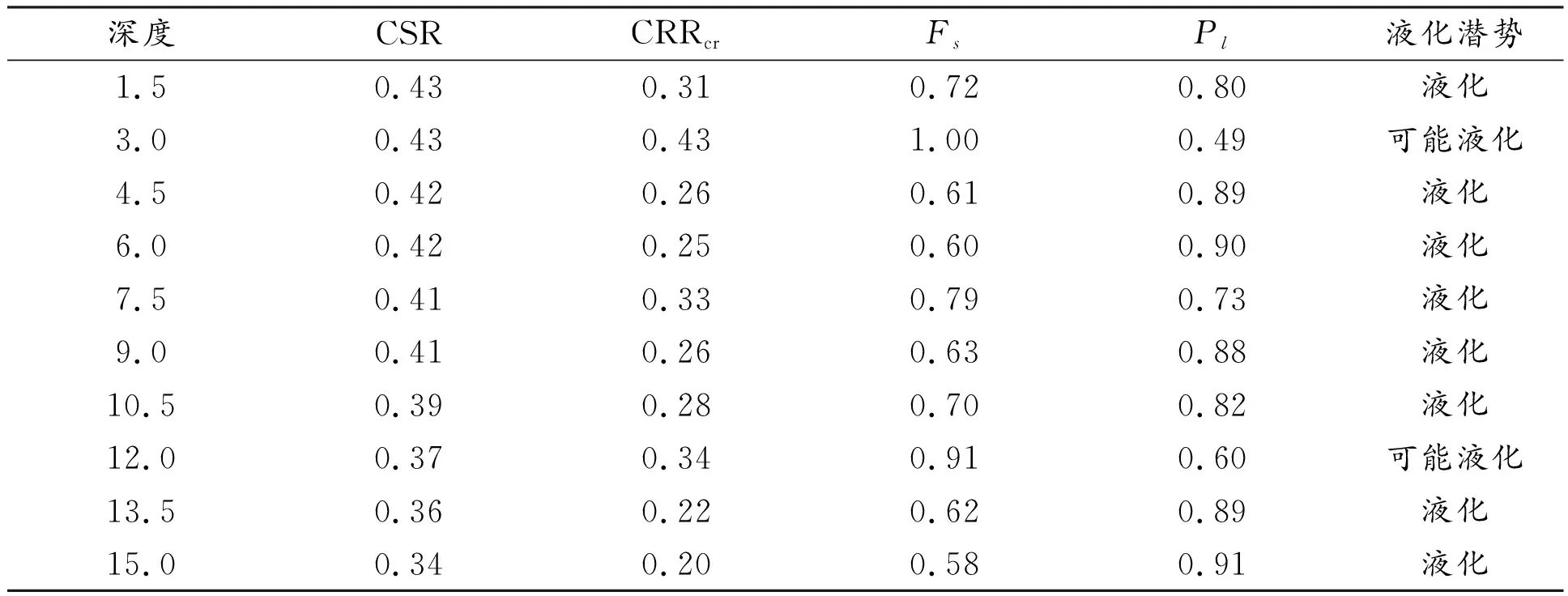
表5 神经网络模型法液化判别结果

2.4 EERC法

Seed和Cetin等应用概率模型考虑多种因素的影响，提出了砂性土液化势概率分析的一个新方法，这里称为EERC(美国伯克利地震工程中心)法。EERC法中按式(10)计算rd值：

(10)

式中：z为土层深度(m)；veq为下面12 m范围内的场地等效剪切波速(m/s)；amax为地面地震动峰值加速度(g)；σ(z)为标准差，按下式确定：

σ(z)=0.0198z0.8500z<12 mσ(z)=0.0198×120.8500=0.1637z≥12 m

(11)

饱和砂土层的液化概率的经验公式按式(12)确定：

(12)

式中：Pa为大气压力；Φ(*)为标准正态分布函数；震级Mw对地震循环应力比CSR的影响仍采用震级标定系数MSF表示，但其取值与NCEER建议的MSF值有所不同，见表6。

参考国内相似海底地层钻孔剪切波速测试结果，确定12 m内等效剪切波速为180 m/s。利用上述模型，钻孔细砂层的判别结果如表7所示。Pl范围为0.002 6～0.997 9，液化潜势评价为不液化～液化，与神经网络法判定结论稍有不同，但液化深度均为15 m。

表6 震级标定系数MSF值

表7 EERC法判别结果

2.5 液化结果分析

以上各类方法的判别结果基本一致，即钻孔15 m内现状细砂层在500 a一遇地震作用下将产生液化现象。

当防浪堤建成后，由于结构物基础附加应力的压密作用，必将改变可液化土层原有的结构和应力状态。实质上，结构建成后砂土的液化判别问题是高有效上覆压力下饱和砂土的液化判别问题。动三轴试验表明，饱和砂土的抗液化强度随固结应力的增大而提高，但两者的关系是非线性的。防浪堤建成后会使基底下可液化土层的抗液化能力增强，而位于基础外侧土体由于结构物的下沉将会产生附加剪应力，削弱其抗液化能力。因此，结构物的存在将会改变地基可液化土层的液化势分布。

结构物对地基土液化性的影响不仅取决于结构物的自身重量与载荷分布、基础形状尺寸、埋置深度，而且还取决于结构物自身的动力特性，影响较为复杂。已有的试验和理论分析表明：基础外侧周围抗液化强度最薄弱，自由场次之，基底以下最强。

3 液化侧向滑移与震陷评估

对于液化产生的侧向位移，Hamada等[11]首先提出经验回归统计方法，该方法通过震害调查，建立地震液化侧向位移数据库，进行统计回归分析，得到经验关系：

(13)

式中：D为侧向地面位移(m)；H为液化层厚度(m)；θ为液化层底面的最大坡度(%)。

由本项目工程勘察资料可得，海底0～-9 m等深线平均坡比为1：65，根据本次钻孔，推测海底可液化细砂层底面(黏土层顶面)平均坡比为1：64，因此可以认为可液化细砂层厚度不变。根据液化判别结果，可液化细砂层厚度约为9～13.5 m。利用式(13)估计地震液化后海底面侧向位移可达2.6～3.2 m。这种侧向滑移，如海底砂土层结构均匀、地形起伏不大，可能在一定区域内表现为近连续变形(滑移)，但也可能受海底地形起伏、砂土层间结构、下卧层影响，呈现分区块、分条带的整体滑移。

对于液化震陷量的估计，采用建筑抗震设计规范中的计算公式：

(14)

式中：SE为液化震陷量平均值(m)；S0为经验系数，对7、8、9度分别取0.05、0.15、0.30；B为基础厚度(m)，当B≤0.44d1时，取B=0.44d1；d1为由地面起算的液化深度(m)；d2为由地面起算的上覆非液化土层厚度液化深度(m)，液化层为持力层取d2=0；p为基底压力(kPa)；Dr为砂土相对密度，可依据标准贯入击数N取值。

基础宽度B取堤心石铺设宽度。由于基础宽度和基底压力都取决于防浪堤断面设计方案，按最不利原则，基础宽度按平均估计，基底压力按防浪堤断面进行计算，估计液化震陷。按式(14)计算，得出的液化震陷量约为35～44 cm。

基于上述计算与分析，考虑斜坡式防浪堤结构形式具有一定自稳调整能力，对地基的承载力要求不高，对地基的不均匀沉降不敏感，堤基范围内地基具有压载加固效应。本研究认为：若遭遇500 a一遇地震作用影响发生地基液化，防浪堤主要的破坏形式为受地基侧向滑移引起的侧向错移，最大错移量不大于3 m；同时会伴有一定震陷，除因海底地形起伏等导致的局部整体滑移形成陡坎外，震陷量不会超过50 cm；防浪堤使用功能可能受到一定程度影响或部分丧失，但不会发生完全丧失使用功能的破坏。

4 结论

以印尼某防浪堤为研究对象，开展砂土地层原位测试与室内试验，依据国内外液化判定方法，综合判定地层液化潜势，并预测液化灾害，得到以下结论：

(1)基于国标法、Seed法、神经网络法与EERC法，在计算砂土液化时，液化潜势评估结论基本一致，15 m内现状细砂层在500 a一遇地震作用下将产生液化。

(2)砂土发生液化时，防浪堤的主要破坏形式包括侧向错移和震陷。最大错移量不大于3 m，最大震陷量不会超过50 cm。防浪堤使用功能可能受到一定程度影响或部分丧失，但不会发生完全丧失使用功能的破坏。