回热器丝网填充率对85 K型同轴脉管制冷机性能的影响分析

赵 鹏 陆 志 蒋珍华 曲晓萍 吴亦农

(1 中国科学院上海技术物理研究所 上海 200083)

(2 中国科学院大学 北京 100049)

1 引 言

本研究以一台单级同轴型脉管制冷机为研究对象,通过建立一维热力学模型,结合调相理论,分析回热器丝网填充率的小范围变化对制冷机相关参数的影响情况,包括回热器内部质量流振幅、质量流与压力波的相位差、回热器内部能量损失、各零件能量损失以及PV功等。同时,对不同丝网填充率进行性能实验研究,以验证模型计算的准确性。

2 一维热力学模型与实验系统

2.1 一维热力学模型

本研究将根据仿真软件建立相应模型,以对脉管制冷机的回热器、惯性管及气库相应参数进行数值模拟计算,来分析各参数与制冷机性能的关系。通过质量守恒、动量守恒、能量守恒及其他相应关系式对各模块分别进行建模,再通过各模块的质量流、能量流、力的关系进行连接,建立制冷机整机模型,可以求解计算制冷量、PV功、质量流、能量损失、相位差等。

本模型为了提高运算效率,将三维控制方程进行一维简化处理,并在方程中加入了许多经研究验证的经验参数来提高模型计算的准确性,为了更高效地进行模拟计算,在脉管制冷机建模时,采用了以下假设:

(1)工质气体氦气为理想状态;

(2)气体的流动简化为一维流动;

(3)忽略制冷机内部的辐射换热、壁面与环境的对流换热及径向导热;

(4)回热器热端及冷端、脉冲管热端温度恒定;

(5)回热器内部填料均匀、填充率在各截面上恒定。

马奴托海在今之何地？马大正和马汝珩在《漂落异域的民族——17至18世纪的土尔扈特蒙古》(中国社会科学出版社1911年第105页)记述“地点大致在阿斯特拉罕以北的伏尔加格勒到里亚尔之间的伏尔加河右岸一带”。此说只是指了一个大体方向，只有面而无点！近年，阿拉腾奥其尔在其专著《清朝图理琛使团与<异域寻> 研究》(广西师范大学出版社，2015年)从两个方面对此做了考证。异域寻

整个系统,通过质量守恒、动量守恒及能量守恒方程进行建模,其关系式分别为:

质量守恒方程:

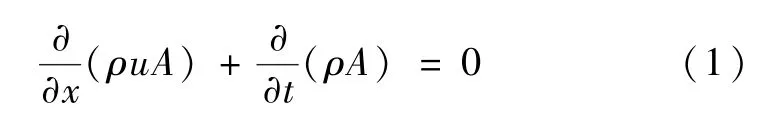
式中:x为位移,m;t为时间,s;ρ为气体密度,kg/m3;A为气体流通截面积,m2;u为气体速率,m/s。

动量守恒方程:

式中:P为气体压力,Pa;F为黏性压力梯度,Pa/m。

能量守恒方程:

式中:Cv为定容比热容,J/(kg·K);Cp为比定压热容,(J/kg·K);α为对流传热系数,(W/m2·K);AL为对流换热表面积,m2;T -Tm为热力学温差,K。

气体的状态方程:

式中:R为气体常数;T为温度,K。

2.2 实验系统

用于脉管制冷机性能测试研究的实验装置如图1所示,分别包括脉管制冷机、温控系统(水冷加高低温试验箱风冷)、真空系统(为制冷量测量提供真空环境)、制冷机驱动电源、测量系统。

图1 脉冲管制冷机实验台Fig.1 Laboratory bench for pulse tube cryocooler

温控系统的作用是为制冷机测试提供环境温度,使制冷机工作在要求温度范围内,散热方式采用高低温试验箱风冷与水冷相结合,其中水冷用于散热面小且发热量大的部位,包括回热器热端和压缩机机座;真空系统主要为制冷机测试提供真空环境,因为制冷机通常工作温度较低(150 K 以下),在其冷头进行冷量测试时,需要保证真空室真空度足够低,以减少对流换热损失,并在冷指外壁面包裹镀铝箔膜,以提高测量精度;制冷机驱动电源和测量系统是制冷机性能测试的核心设备,主要包括交直流驱动电源、直流加热电压、测温与加热模块、数据采集仪。

实验用12 W@85 K 同轴型脉管制冷机如图2 所示。压缩机为线性对置式动圈结构,使用交流电源进行驱动,活塞直径为Φ20 mm,最大行程为4.5 mm;冷指为同轴型结构,脉冲管置于回热器内部;调相机构为惯性管加气库的结构,其中惯性管为紫铜管材质,由两段不同长度和内径的铜管焊接在一起,气库为圆柱形,惯性管通过法兰接头与气库连接。

图2 实验用同轴型脉管制冷机1.压缩机;2.连管;3.气库;4.惯性管;5.水冷管;6.真空管;7.波纹管。Fig.2 Coaxial pulse tube cryocooler for experiment

3 模拟计算及实验结果分析

在模拟计算和实验过程中,制冷机的制冷量为12 W@ 85 K,充气压力为3.5 MPa,工作频率为60 Hz,环境温度为296 K。

3.1 填充率对回热器热端及冷端质量流振幅的影响

在保持恒定12 W@85 K 制冷量时,回热器丝网填充率的改变对回热器冷热端质量流振幅的影响如图3 所示。随着丝网填充率的增加,回热器热端质量流振幅和冷端的质量流振幅均同步减小,主要原因在于随着丝网填充率的增大,压缩机活塞所需的运动行程减小,因此其输出的质量流振幅减小,而另外一方面也说明增大丝网填充率对回热器的蓄冷能力影响不大。

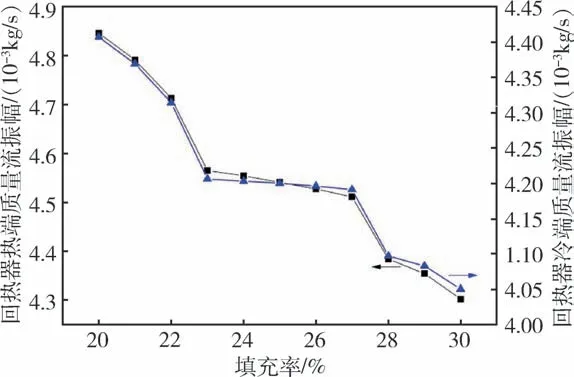
图3 回热器热端、冷端质量流振幅与填充率的关系Fig.3 Relationship between the mass flow amplitudes of hot and cold ends of regenerator and filling rate

3.2 填充率对回热器热端相位差及冷端相位差的影响

回热器丝网填充率的改变对回热器热端质量流与压力波的相位差、回热器冷端质量流与压力波的相位差的影响如图4 所示。随着丝网填充率的增加,回热器热端相位差变小,同时冷端相位差也变小,说明整机整体的相位相对于理论相位有向下移动的趋势,但是两者变化的幅值均较小,说明丝网填充率的改变对相位角的影响较小。

图4 回热器热端相位差、冷端相位差与填充率关系Fig.4 Relationship between phase difference of hot and cold ends of regenerator and filling rate

3.3 填充率对回热器内部能量损失及其它零部件能量损失的影响

回热器丝网填充率的改变对回热器能量损失以及制冷机各零部件能量损失的影响如图5 和图6 所示。首先,回热器压降损失的比重以及变化幅值均远大于表面换热损失及轴向导热损失(轴向导热损失在2.27—2.13 W 之间,且随着填充率的增大而减少)。回热器的压降损失随着丝网填充率的增大而显著增大。根据水力直径的定义可知,随着丝网填充率的增大,编织丝网的水力直径也随之减小。再根据Clark J A[6]提出的压降经验公式可知,水力直径越小,则压降将随之增大,从而导致压降损失增大;其次,回热器表面换热损失随着填充率的增大而减小(变化幅值在15.78—9.07 W 之间),说明改变丝网填充率对表面换热损失有一定影响,主要原因在于随着不锈钢丝网填料的水力直径减小(而此时的工质气体热渗透深度不变),工质气体与填料丝网的换热损失减小,从而导致表面换热损失的减小;最后,除了回热器的损失相对较大外,惯性管及其他零部件的损失各有升降,且幅值相对较小,主要受回热器冷热端的质量流振幅及相位差改变影响。

图5 回热器压降损失及表面换热损失与填充率关系Fig.5 Dependence of pressure drop and surface heat transfer losses of regenerator on filling rate

图6 各零部件能量损失与填充率关系Fig.6 Variation of energy loss of each component with filling rate

3.4 填充率对制冷机性能的影响

分别进行了24.8%、25.5%、26.37% 填充率的制冷性能测试实验和数值模拟计算。回热器丝网填充率的改变对制冷机的性能影响如图7 所示,模拟计算的PV功以及实际实验的输入功均随着丝网填充率的增加而增大,模拟计算的PV功基本呈现为线性趋势,填充率从25.5% 增加到26.37% 时,实际输入功曲线斜率有一定增大。填充率从24.8% 增大到26.37%时,实际输入功变化幅值为3.1%,数值模拟计算的理论PV功变化幅值为1.6%,实际输入功变化幅值比PV功变化幅值要大,原因在于:当填充率增加到26.37% 时,需要填充更多的丝网数量,丝网需要用较大力才能压平,会导致丝网存在轻微变形,同时也会导致丝网呈现下松上紧的状态,增大回热器内部能量损失,从而导致实际输入功增幅比模拟计算结果大。

图7 PV 功和COP 与填充率关系Fig.7 Dependonce of PV power and actual power on filling rate

4 结 论

本研究建立了一维脉冲管热力学模型,分析了填充率改变对制冷机回热器冷热端质量振幅、回热器冷热端的相位差、回热器压降损失及表面换热损失、各零件的能量损失、理论PV功的影响规律,并进行了实验验证。研究发现,将丝网填充率由24.8% 提高到26.37%,制冷机的性能发生衰减,主要原因在于:随着丝网填充率的增大,编织丝网的水力直径也随之减小,从而造成回热器压降损失的增大。此外,填充率增加到26.37%时,实验的实际输入功有一定程度增大,主要原因在于:当填充率增加到26.37%时,需要填充更多的丝网数量,丝网需要用较大力才能压平,导致丝网存在轻微变形,同时也会导致丝网呈现下松上紧的状态,会增大回热器内部能量损失,从而导致实际输入功增幅比模拟计算结果大。