利用数形结合解函数问题的一般方法
周利平


摘要:函数是中学生在数学学习与研究中最常见的一类问题,因此函数问题也是中学生所必须克服的难关。函数问题的题型种类多,而且灵活度高。
关键词:数形结合,函数,最值,零点。
数形结合的思想方法是充分运用数的严谨和形的直观,将抽象的数学语言与直观的图形语言结合起来,是抽象思维和形象思维相结合,通过图形的描述、代数的论证,来研究和解决数学问题的一种数学思想方法,数形结合思想的应用,包括以下两个方面:
1、以形助数
即借助形的直观性来阐明数之间的联系。以形助数常用的有:借助数轴,借助函数图象,借助单位圆,借助数式的结构特征,借助解析几何方法。
2、以数助形
即借助数的精确性来阐明形的某些属性。以数助形常用的有:借助几何轨迹所遵循的数量关系,借助运算结果与几何定理的结合。
函数是中学生在数学学习与研究中最常见的一类问题,题型种类多,而且灵活度高,所以懂得如何利用数形结合的思想解决函数问题就成为中学生所必备的能力。下面从以下几个方面来阐述数形结合解函数问题的一般方法。
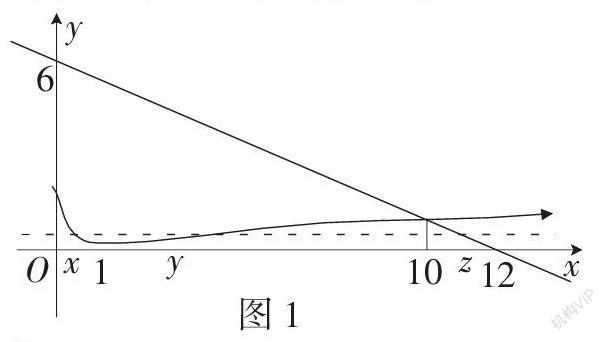
一、利用函数模型求参量取值范围
函数参量方程在函数问题中最为常见,也是比较难的,利用数形结合的方式将参量表示出来,就可很清晰的确定参量的取值范围,方便了计算,也明确了做题的思路。
二、利用函数模型求最值问题
对于求函数的最值问题,利用数形结合的方法便可以很直观地表示出函数的最值。
例2:求解函数的最大值和最小值。
解析:先把函数解析式变形,这就可以当作是定点M(-6,-4)与单位圆上的N(cosx,sinx)连线的斜率。因此,最值就是直线AN与单位圆相切时的斜率。
将与圆:X2+Y2=1相切斜率为l切线方程设为y=lx±由于切线过定点M(-6,-4),则-4=-6l±,,.
三、利用数形结合思想求解函数零点问题
求解函数的零点的个数是高中学习中常见的题型,而运用数形结合的思想方法来解答这个问题是最为直观的方法。
例3:求f(x)=lgx-sinx,在[0,10]上的零點个数。
解析:对于这道例题来说,画出函数图象,看它和x轴的交点是比较困难的。但是要是画函数f(x)=lgx与f(x)=sinx的图象则是比较容易的,于是我们想到分别画出两条函数的图象,这样观察两条函数图像的交点就可以求解这个问题。
通过观察图象就很容易发现函数f(x)=lgx与f(x)=sinx在x∈[0,10]交点的个数为3个,所以函数f(x)=lgx-sinx在[0,10]上零点的个数为3个。
数形结合就是将数与形结合在一起,使得抽象的思维和形象的思维并存,充分将二者之间的优劣势互补,至此达成一种最佳的思考方式。应用数形结合的思想可以将繁琐问题简单化,抽象问题直观化,从而以最明了的方式解决数学问题。
参考文献:
[1]徐国央.数形结合思想在数学解题中的应用[J].宁波教育学院报,2009,(01).
[2]杨琴.高等数学教学中应重视数形结合思想的作用[J].才智,2009,(15).
[3]刘雨智.浅谈数形结合在解题中的应用[J].各界(科技与教育),2009,(02).
[4]曾剑华.浅淡数形结合在函数教学中的应用[J].科技创新导报, 2009,(14)

