基于预测风险场的智能汽车主动避撞运动规划*

王安杰，郑 玲，李以农，王 戡

（1.重庆大学汽车工程学院，机械传动国家重点实验室，重庆 400044；2.重庆车辆检测研究院有限公司，重庆 401122；3.汽车主动安全测试技术重庆市工业和信息化重点实验室，重庆 401122）

前言

自动驾驶技术已成为汽车行业的热门研究课题，据调查显示，90%左右的碰撞事故是人为因素造成的［1］。自动驾驶技术可以避免人为因素造成的交通事故，提高安全性和便利性。同时，为不因引入自动驾驶技术而造成新的安全隐患和事故，自动驾驶技术本身的安全性和可靠性至关重要；完备的运动规划可保证自动驾驶的可靠性，运动规划也是自动驾驶的关键技术之一。

运动规划旨在考虑环境状态变化的前提下，为车辆规划出一条满足初始状态、目标状态以及速度、加速度、曲率等约束的无碰撞路径。Lee等［2］提出了一种预测占用图的风险评估方法，结合加速度轨迹采样筛选得到风险最小的安全轨迹。Kim等［3］提出了一种识别周围环境潜在风险的方法，并借此找到风险最小的安全路径。任玥等［4］引入虚拟力场，提出了基于模型预测理论的避障路径规划方法，表现出良好的鲁棒性。朱冰等［5］提出了安全场引导的RRT*算法，减少了计算量，提高了收敛速度。肖浩等［6］借鉴人工势场理论思想，提出了一种基于危险斥力场的主动避撞局部路径规划算法，具有运算量小、安全可靠的特点。修彩靖等［7］改进了传统人工势场法，建立了考虑道路约束和车辆约束的目标函数，既消除了抖动问题，又满足了安全指标。Kim等［8］基于车辆目标车道概率的运动预测来定量评估一组候选路径的碰撞风险，该风险评估算法可以估计与周围车辆即将到来的碰撞风险。Hesse等［9］结合势场法和弹性带理论，并将车辆动力学引入到弹性带中，提出了一种扩展的弹性带路径规划方法。Houenou等［10］提出了一种基于恒定横摆角速度、恒加速度模型和基于行为识别相结合的轨迹预测方法，使短期和长期轨迹预测都具有较好的精度。张一鸣等［11］结合驾驶意图和物理运动模型完成了轨迹预测以及车辆运动规划。Werling等［12］针对结构化道路，结合五次多项式和最优控制，提出了一种在Frenet坐标系下的直接轨迹生成方法。

以上避撞运动规划的风险势场主要为道路纵向和横向上的风险评估，局限于当前状态，未能准确描述障碍物风险随时间的变化趋势。且主要着重于前方障碍物研究，关于侧方和后方障碍物对本车的碰撞风险关注不足。

针对高速紧急工况，本文中在考虑场景预测的前提下，提出了考虑时间因素的预测风险场，用于描述障碍物风险及其随时间的变化趋势，包括侧方和后方障碍物。并据此建立基于动态规划和二次规划的直接轨迹生成运动规划方法，以保证车辆在紧急工况下的安全性和稳定性。

运动规划架构如图1所示，融合场景预测信息在纵向、横向以及时间3个维度下建立了用于风险评估的预测风险场，包含障碍物风险评估、道路环境风险评估和稳定性风险评估；并在各项约束下，使用动态规划完成本车行为决策，得到一条分段线性的决策轨迹；以决策轨迹为参考轨迹，利用多项式曲线和二次规划方法对轨迹进行优化处理，实现主动避撞运动规划。

图1 基于动态风险评估的运动规划架构

1 坐标转换

为便于在弯道下进行碰撞风险评估，须将Cartesian坐标系下的车辆坐标、航向角信息转换到Frenet坐标系下。如图2所示，P点代表车辆位置，A、B两点分别表示道路参考线的起点和终点，且道路参考线的Cartesian坐标和Frenet坐标、车辆的Cartesian坐标均已知。表1为求解车辆位置P点Frenet坐标系下坐标和航向角的伪代码。考虑实际行车工况，在道路半径大于100 m、且车辆位置偏离参考线不超过10 m的情况下，取搜索精度ε为0.001 m，任意车辆可在6次迭代之内找到唯一投影坐标。

图2 车辆在Frenet坐标系下的投影

表1 Frenet坐标投影搜索算法

将车辆投影到Frenet坐标系并完成局部路径规划后，规划的轨迹需要转换到Cartesian坐标系下进行评估以及后续跟踪［12］。式（1）为坐标、航向角和曲线从Frenet坐标到Cartesian坐标的转换所需信息。

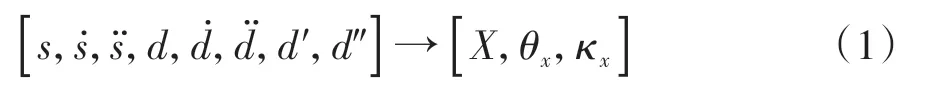
图3为Frenet坐标系下的轨迹转换。式（3）为坐标转换关系式。式（4）和式（5）为Cartesian坐标下的航向角和曲率转换关系式。

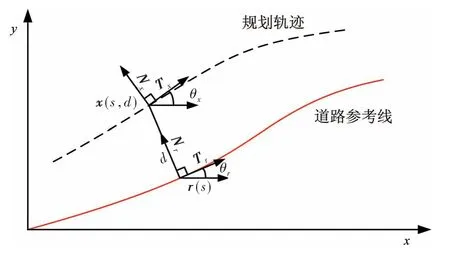
图3 Frenet坐标系下的轨迹转换

式中：Δθ=θx-θr，假设车辆轨迹一直沿参考线附近运动，则有|Δθ|＜ π/2，1-κrd＞0；κr和κ'r分别为参考线某一点在Cartesian坐标系下的曲率和曲率变化率。当参考线用参数曲线表示时，其κr和κ'r可用式（6）和式（7）表示。

结合式（2）～式（7）可得规划轨迹上某一点在Cartesian坐标系下的坐标、航向角和曲率。

2 动态风险评估模型

2.1 车辆运动预测

在评估本车在动态环境下的风险时，须根据交通参与者的类型、位置、速度和加速度等信息预测其未来一段时间内的运动规律。场景预测包含动态物体和静态物体的运动预测。研究表明，基于物理规律的运动模型可以有效预测物体运动轨迹，但仅限于短期的碰撞风险预测［13］；因此本文选择短时间内精确度较高的CA模型作为车辆运动预测模型，其表达式为

假设预测时长为tn，将时间离散化后代入CA模型即可求得车辆位置序列的预测轨迹。同时，为在同一时刻判断本车风险，给出相同时间序列下的本车轨迹点，即运动规划得到的轨迹序列。

2.2 障碍车风险评估

障碍物风险模型如式（9）所示，将障碍车风险评估划分为5个区域，如图4所示。

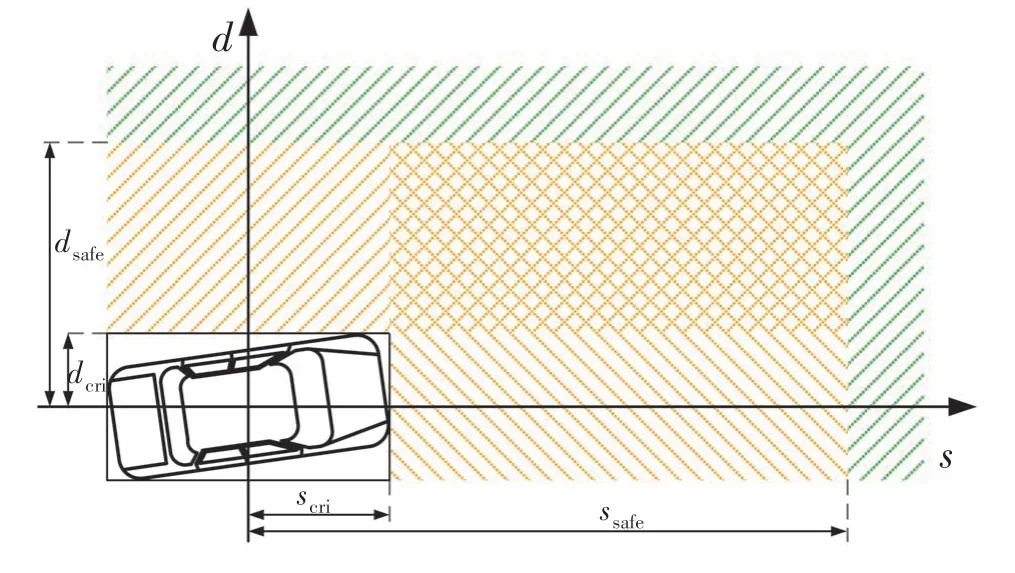
图4 障碍车风险评估示意图

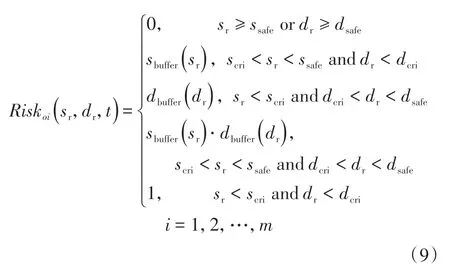
式中：sr和dr分别为同一时刻下本车与障碍车的纵向相对距离和横向相对距离，均为绝对值；ssafe和dsafe分别为本车应与障碍车的纵横向安全距离，其具体数值由相应场景决定，大于此值时风险值为0；scri和dcri分别为障碍车矩形膨胀框长宽的1 2，小于此值时风险值为1；sbuffer和dbuffer为单调递减函数，描述从碰撞到安全区域风险逐渐降低的变化过程；m为障碍车数量。以纵向为例，将上述参数定义如下：

式中：θobs为障碍车航向角；Lobs和Wobs分别为障碍车的长和宽；egocri为本车矩形膨胀框长度的1 2；vr为相对速度；ksv为安全碰撞时间余量，物理意义与TTC相同；此处也可用安全车间时距来获取安全距离；smin为纵向相对速度为0时的最小安全距离。

最后，将所有障碍物的风险进行整合。即在同一时刻，障碍车在Frenet坐标系下某一点处的风险用所有障碍物在该点处的风险最大值表示，如式（13）所示。

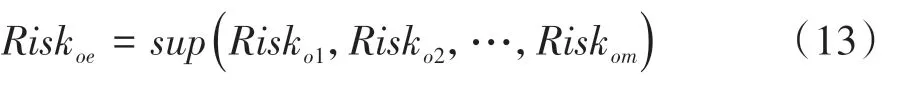
2.3 道路环境风险评估

在没有其他障碍物时，道路对本车的影响因素主要考虑车道线以及道路左右边界位置，道路边界的危险程度是高于车道线的，而每条车道中心的位置应是没有风险的，势场值是最低的，车道线主要用于约束车辆行驶于车道中间。因此采用三角函数构建道路的风险模型［14］。道路风险模型仅与车辆的横向坐标d有关，如图5所示。

图5 道路风险势场

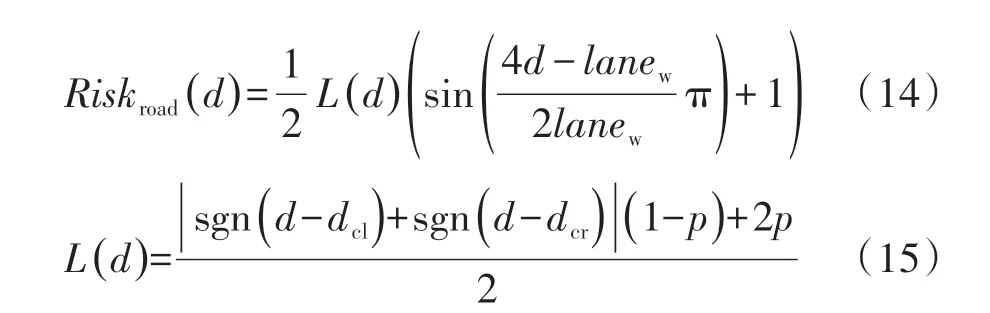
式中：lanew表示车道宽度；p为车道线处的风险值，用于约束本车的换道意图，其值大小与车道线类型有关，比如，白色虚线处的风险值最小，双黄线的风险值最大；dcl和dcr分别为最左侧和左右侧车道中心线处的横向坐标值。

2.4 稳定性风险评估

本车过大的纵横向加速度存在一定的稳定性风险，可能导致侧滑或侧翻事故；且横向风险大于纵向风险，因此用椭圆描述纵横向加速度稳定性安全区域。式（16）为稳定性风险模型。其中：μ为路面附着系数；g为重力加速度；aengine为本车的最大加速度；as和ad分别为纵横向加速度；assafe和adsafe分别为安全椭圆长半轴和短半轴长度；aellipse为a到原点连线与安全椭圆交点处的加速度值。图6为稳定性风险势场。

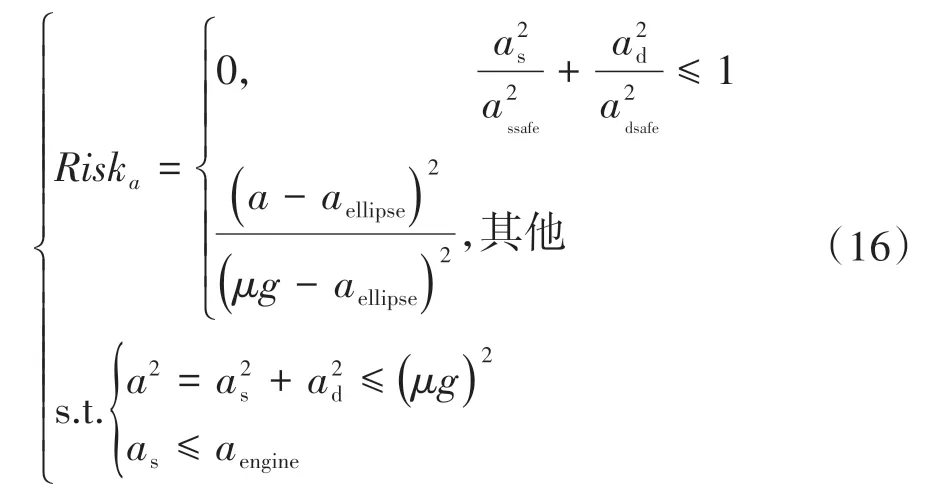
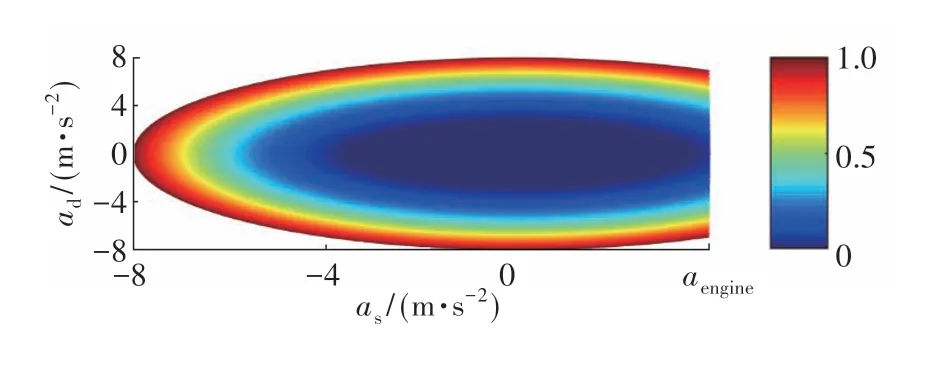
图6 稳定性风险势场

2.5 预测风险场

将周围车辆风险模型、道路环境风险模型和稳定性风险模型合并为预测风险场（PRF）模型。式（17）为预测风险场的计算方法。

表2为三车道示例场景，假设本车不做任何避撞操作，沿当前车道匀速行驶。t=0 s时刻下障碍物风险势场如图7所示，图中蓝点为当前时刻本车位置，本车与前车、后车的势场值相等。0.5 s之后的风险势场如图8（c）所示，由于前车有4 m/s2的减速度，此时本车与前车的势场值最大，对本车的威胁最高，符合驾驶经验。

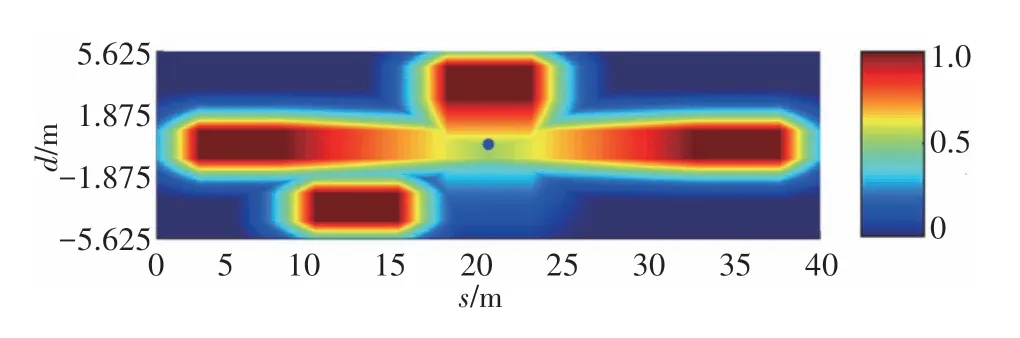
图7 障碍车风险势场

图8 预测风险场

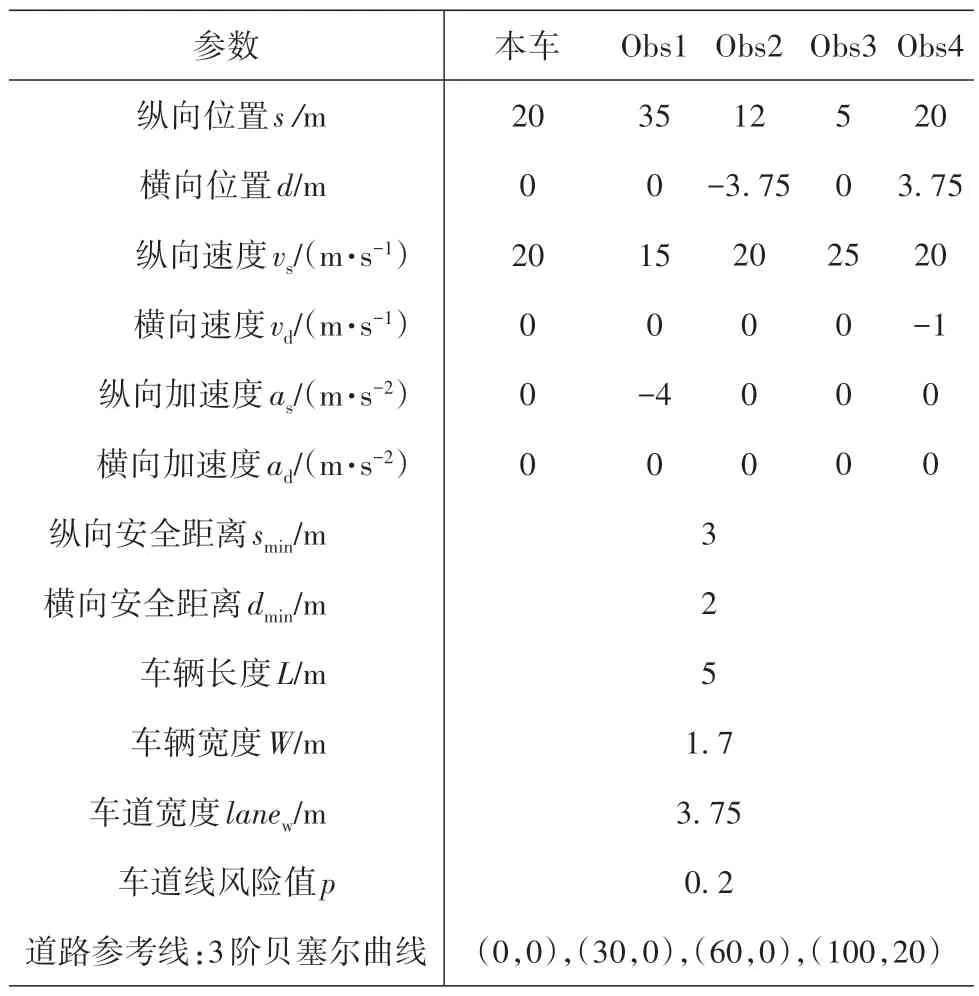
表2 三车道示例场景

3 运动规划

3.1 行为决策

使用动态规划（dynamic programming，DP）进行车辆的行为决策［15］。行为决策就是根据车辆周围的动态环境信息决策出本车的驾驶行为和目标点位置［16］。本文以时间作为阶段变量k的划分依据，相邻两个阶段的时间间隔为dt，将车辆的行为决策问题划分为相互联系的n个阶段，当前时刻t0作为最后一个阶段，末时刻tn作为第一阶段；以Frenet坐标系下的纵向坐标和横向坐标作为状态变量x（s，d）和决策变量dec（s，d）。如图9所示，行为决策主要包含允许状态集合与允许决策集合、指标函数和动态规划求解。

图9 基于动态规划的行为决策框架

为满足路面附着要求以及本车加速性能限制，纵横向加速度须满足式（18）。

式中：tk为阶段k对应的未来时刻；x0和v0分别为初始位置和速度；alimit和xlimit分别为加速度极限和在tk时间内能到达的极限位置。

依据式（19）可得车辆每个阶段在道路中所能到达的位置，即允许状态集合，如图10所示。且在正常行车时不会出现倒车情况，所以Smin一定大于当前时刻纵向坐标。同理，将tk替换为dt，用限速值代替初速度，以当前状态作为初始位置，即可得到某一状态下的允许决策集合D。

图10 阶段k的允许状态集合示意图

得到允许状态和决策集合后，须确定指标函数以衡量阶段的决策效果，如式（20）所示。阶段指标函数ck(xk，deck)表示在第k阶段处于xk状态下执行决策deck后的效果，f（xxk）为最优指标函数，是求解最优决策序列的重要依据；Tk为状态转移方程，用于获取执行决策后的车辆位置状态。

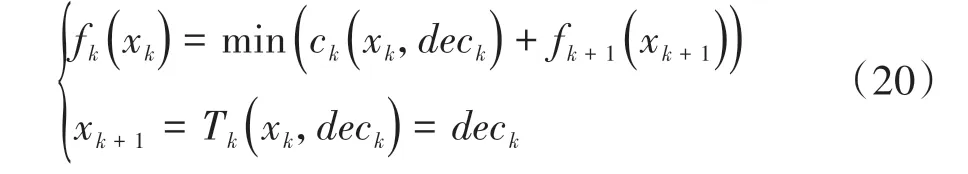
阶段指标函数定义如下：

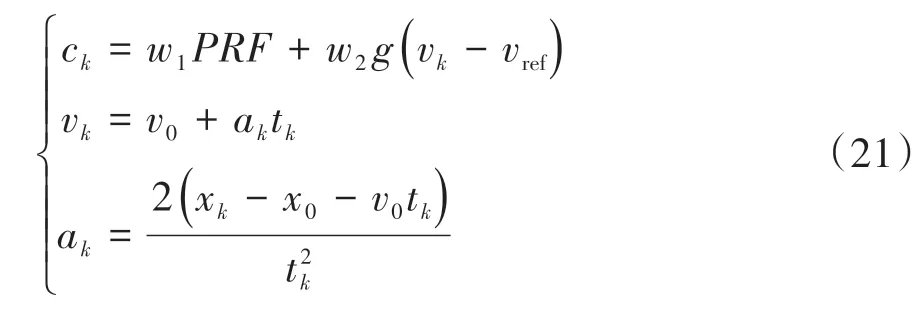
阶段指标函数的第1项为建立的预测风险场函数，vk和ak分别为初始时刻到当前时刻的平均速度和平均加速度；参考速度vref与交通规则、道路曲率有关；g为速度保持函数，本车速度高于vref时的代价比低于vref时大。

动态规划搜索过程就是利用式（20）递推关系式的一个逆序递推计算求解过程。即从最后一个阶段开始，依次计算由当前阶段到最后一个阶段最优指标函数值最小的状态序列，最终获得离散的三维轨迹序列。

3.2 轨迹规划

由于分段线性的DP轨迹无法满足速度连续性要求，因此，使用多项式曲线对轨迹进行优化处理和速度规划。如图11所示，主要包含构造二次规划（quadratic programming，QP）模型和轨迹检测，并通过迭代得到一条满足速度、加速度、曲率约束的无碰撞轨迹。

图11 基于二次规划的轨迹规划框架

二次规划模型主要根据DP轨迹、平滑指标、车辆动力学约束、交通规则，依据多项式曲线构造，纵横向轨迹用式（22）的多项式曲线表示，目标函数和约束条件如式（23）所示。

式中：s0、vs0、as0分别为初始时刻纵向位置、速度和加速度；d0、vd0、ad0分别为初始时刻横向位置、速度和加速度；sn、dn为末时刻的纵横向坐标，由行为决策的目标点位置决定；vmax为限速值，用纵向速度近似代替。目标函数第1项表示在对应时刻多项式曲线和DP轨迹之间距离；第2项是稳定性指标，也可衡量轨迹的平滑度。最后两项为纵横向加速度约束，为满足线性约束要求，做了放大处理。

轨迹检测是为确定优化轨迹满足加速度约束、曲率约束以及无碰撞要求。加速度须满足式（18）。曲率约束如式（24）所示，曲率须将轨迹转换回Cartesian坐标系计算，κmax为允许的最大曲率，由前轮最大转角决定。

某一时刻的碰撞检测如图12所示。在sdz坐标系中，用虚线矩形对车辆做膨胀处理，以描述车辆的碰撞安全裕度。本车膨胀矩形不变，障碍车的膨胀矩形随时间逐渐变大。通过判断本车4个顶点是否在障碍车膨胀框内来判断碰撞；以E1点为例，分别计算向量O1O2、O2O3、O3O4、O4O1与向量O1E1、O2E1、O3E1、O4E1的向量积，若所得结果中有z值大于0，则E1点在外部。若本车4个顶点都在外部则无碰撞；否则，该时刻极有可能碰撞。

图12 碰撞检测示意图

4 仿真分析

仿真场景使用三车道、四障碍车的直道场景，针对高速场景下纵向和横向障碍车快速靠近本车的危险工况，对所提出的运动规划方法进行仿真验证。

4.1 纵向避撞工况

纵向避撞工况场景如图13所示。参考速度为25 m/s。本车在中间车道，中间车道前方和后方都有车辆快速接近本车，且前车有制动，左右车道各有一辆车匀速行驶，与本车同速。

若本车不采取避撞措施，2 s后必然发生碰撞。基于预测风险场的运动规划结果如图14（a）所示，由d-t视图可知，决策轨迹横向为换道避撞的形式，且识别出右车道车辆相对距离较远，风险较小，选择向右车道换道；由s-t视图可知，由于本车当前速度低于参考速度，决策轨迹在换道过程中纵向速度表现为先减速再加速。优化轨迹速度和加速度如图14（b）和图14（c）所示。在纵向避撞工况中，侧向加速度未超过稳定性极限。横向上与决策轨迹一致，且轨迹合加速度和曲率均在约束范围内；在多项式曲线作用下，且安全无碰撞时纵向上表现为轻微加速。该运动规划方法能识别后方及侧方车辆的风险，并一次性满足速度、加速度和曲率等约束，直接规划出一条安全无碰撞轨迹。

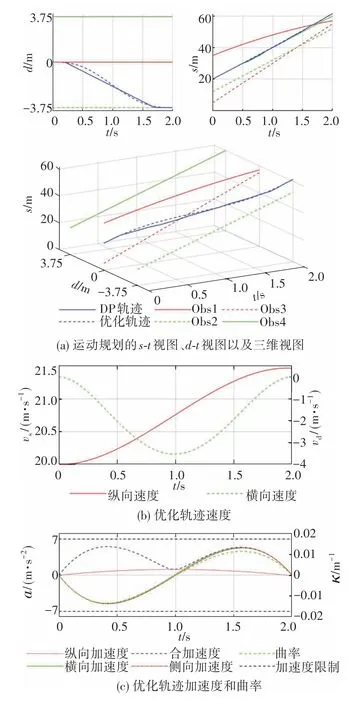
图14 纵向避撞工况

4.2 横向避撞工况

横向避撞工况场景如图15所示。本车速度为25 m/s，已达到参考速度；4辆障碍车与本车同速左右车道各有2辆障碍车，且本车左侧有一辆障碍车以1 m/s的相对速度靠近本车。

图15 横向避撞场景

基于预测风险场的运动规划结果如图16（a）所示。由d-t视图可知，决策轨迹横向上表现为向右轻微避让后返回中间车道；由s-t视图可知，决策轨迹目标点的纵向坐标小于本车匀速到达的位置，因此纵向上表现为减速，这是因为高于参考速度时的代价比低于参考速度时大，且加速能力有限。优化轨迹速度和加速度如图16（b）和图16（c）所示。侧向加速度很小，不存在侧滑风险，横向上与决策轨迹基本一致，在加速度约束下，以非常小的速度向右轻微避让后返回中间车道；在多项式曲线作用下，纵向上表现为以较大的减速度制动避让障碍车。综上所述，根据预测风险场能准确识别出周围车辆潜在风险随时间的变化趋势，实际完成紧急工况下主动避撞的运动规划，且规划结果符合实际驾驶操作，保障了本车在危险工况下的安全性和稳定性。

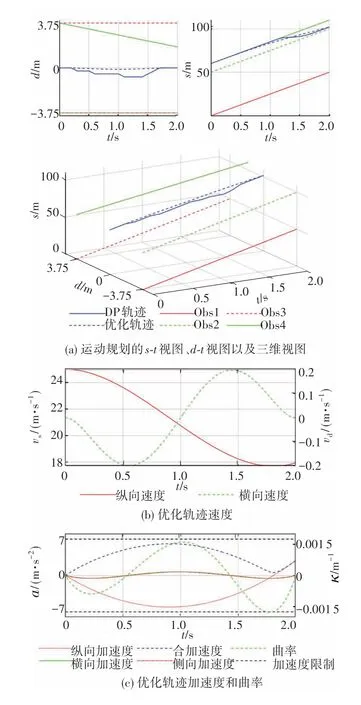
图16 横向避撞工况

5 结论

针对自动驾驶汽车侧方和后方车辆对本车的碰撞风险，在Frenet坐标系下，提出了融合障碍物运动预测的预测风险场，依据此风险评估方法设计了主动避撞运动规划方法。

仿真结果表明：所构建的预测风险场能全面反映本车行驶的碰撞风险和稳定性风险，且能准确识别侧方和后方车辆在不同相对位置和相对速度下的碰撞风险差异以及碰撞风险随时间的变化趋势；运动规划方法依据预测风险场能准确、直接地决策出风险最小的安全轨迹和目标点位置，并规划出满足各项约束的主动避撞轨迹，保障车辆运行的安全性和稳定性。

本文中运动预测使用的是短时间精度较高的恒加速度模型，随着预测时间增加精度降低；由于车辆正常行驶时处于紧急工况的时间很少，因此下一步工作将考虑提高运动预测精度，将运动规划扩展到非紧急工况下。