基于双五次多项式的智能汽车换道轨迹规划*

牛国臣，李文帅，魏洪旭

（中国民航大学机器人研究所，天津 300300）

前言

车道变更作为智能汽车自动驾驶时最常见的驾驶行为之一，在很大程度上影响道路的流通性和安全性。安全、快速且平稳的换道行为可提高通行效率，减少交通事故的发生［1］。合理的换道轨迹是智能汽车安全完成换道任务的前提，同时其性能也决定了换道过程的安全性、高效性和舒适性。

常用的智能汽车轨迹规划算法［2］包括基于搜索的算法［3］、基于弹性带理论［4］和基于参数化曲线的算法［5］等。前两类算法所得到的解不一定是全局最优解，并且实时性较差，不能满足智能汽车高实时性的要求。基于参数化曲线算法中的参数化曲线包括：圆弧曲线［6］、螺旋曲线、Bezier曲线［7］和多项式曲线［8］等。该类算法具有运算量小、直观、精确等优点，也被广泛应用于智能汽车的换道轨迹规划研究中。文献［9］中针对高速道路上的换道行为提出了基于高斯分布的换道模型和最小安全距离模型，用于换道轨迹规划，并混合了决策和控制理论，提出了基于自适应巡航控制（ACC）的轨迹跟踪控制方法用于轨迹跟踪，取得了很好的跟踪效果，但该方法得到的轨迹的横向速度和横向加速度较大。文献［10］中采用一种基于阻力网络的新路径规划方法完成车道保持或变更等行为，其中引入类人因素模拟不同类型的驾驶者，如积极型、温和型和保守型。但该方法的规划时间较长，实时性较低。文献［11］中提出了加速换道模型，将道路上的交通流进行分组，并在V2V的帮助下进行多车协同的换道轨迹规划。但该方法对交通环境和车辆硬件要求比较苛刻，并不能广泛应用。文献［12］中利用三次多项式得到轨迹簇，利用聚类的思想进行多目标优化，从中选取最优轨迹，但该方法计算繁琐，换道舒适性不高。文献［13］中结合人工势场法（APF）和弹性带理论，能在多种道路环境下完成路径规划，并保证轨迹的平滑性，但未考虑车辆在始末时刻航向角的变化过程。文献［14］中提出一种基于多项式函数的轨迹规划算法，设置了加速度约束，建立了速度边界和路径时间最优的多项式参数化仿真模型，为后续的动力学模型研究提供参考。文献［15］中在车辆运动学方程的基础上提出了一种基于六次多项式的轨迹规划算法来考虑避障，但该算法的阶次较高，待定系数较多，计算复杂且收敛速度较慢。文献［16］中对其他学者所研究的换道轨迹的性能进行了对比，最终结论为使用五次多项式规划的换道轨迹综合性能最优。文献［17］中提出一种基于五次多项式的算法，该算法通过增加阶次避开障碍车实现换道，此算法具有较好的实时性，但过程较复杂且计算量大。文献［18］中采用3⁃D Bezier曲线进行换道的路径规划，并将换道的路径规划分为两段，避免换道过程中与障碍物发生碰撞，再进行速度规划，使换道过程的速度满足一系列约束，但将轨迹规划分为路径规划和速度规划会忽略一部分的运动学和动力学特性。

综上所述，五次多项式被广泛用于换道轨迹规划，在避障换道时普遍采用增加阶次的方法避免发生碰撞，但该方法计算繁琐，规划时间增加，安全性降低。为解决以上问题，本文中提出了基于双五次多项式的智能汽车换道轨迹规划算法，通过提出的舒适性约束改进五次多项式规划算法，增加换道过程的舒适性，采用双五次规划的换道策略，保障换道过程安全性的同时又提高了规划算法的实时性。

1 无障碍换道轨迹规划

进行换道轨迹规划时，首先分析无障碍换道轨迹规划，此时换道车周围无其他车辆，如图1所示。

图1 无障碍换道轨迹规划示意图

图中C0是换道车，换道过程为C0车从本车道的中心线行驶到相邻车道的中心线上。仅根据换道车的起始状态Sin和Sfin目标状态，经计算便可得到一条光滑的换道轨迹［19］：

基于五次多项式的特性，分别在x方向和y方向选取五次多项式表示换道轨迹函数：

定义时间参数矩阵：

式中：tin为换道初始时刻；tfin为换道完成时刻。

定义系数矩阵分别为

为保证换道车的平稳运动，须为轨迹函数提供以下边界条件：

式中T为换道过程持续的时间。

结合边界条件和约束条件，再联合式（2）、式（3）、式（6）和式（7）可求出系数矩阵A、B：

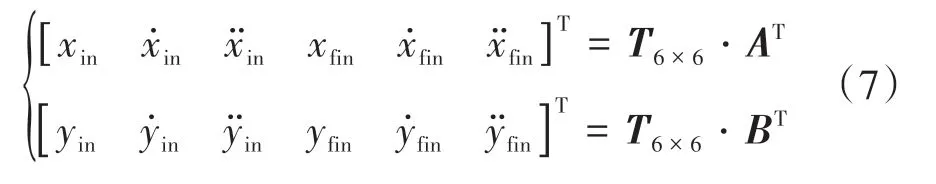
利用求得的系数矩阵，求式（7）解方程组，即可得到无障碍换道时智能汽车的换道轨迹。

为提高换道过程的舒适感，本文中结合实际运动过程中车辆动力学特性的约束［20］、GB/T13441.1—2007［21］中关于舒适性感受的近似描述和加加速度对乘车舒适性的影响［22］，提出了如下换道过程的舒适性约束。

（1）设置换道轨迹的加速度(m/s2)约束：

（2）对换道轨迹的加加速度j(m/s3)的最值进行约束，保证换道过程中速度变化平滑和较好的舒适感。例如无障碍换道时：

在舒适性约束的基础上重新调整换道时间，改进五次多项式规划，优化轨迹性能直至满足约束，如图2所示。

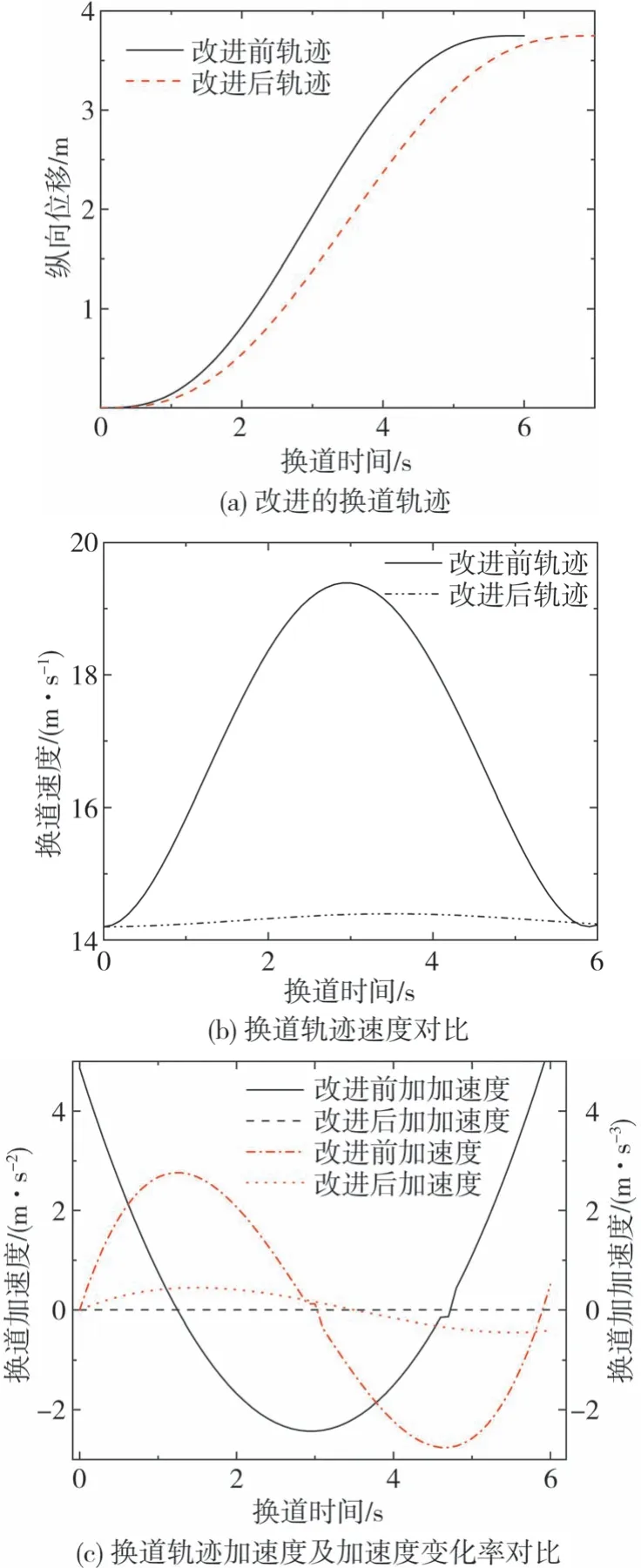
图2 改进五次多项式

具体的无障碍换道轨迹规划步骤如图3所示。

图3 无障碍换道轨迹规划步骤

2 避障换道轨迹规划

智能汽车行驶在结构化道路上时，主要的障碍物为交通车辆，如图4所示，则避障换道规划主要考虑如何避免换道车C0在换道过程中与交通车C1发生碰撞。

图4 避障换道状况示意图

针对避障换道的情况，本文中提出了双五次多项式换道轨迹规划算法，将换道过程分为两个改进五次多项式规划过程，完成首次规划时，换道车到达预先设计的换道中转位置，该次规划的横向位移大于交通车车身宽度，此后换道车进行第二次规划时与交通车在纵向上再无交集，避免换道过程中与交通车辆发生碰撞，简化计算。该算法的思路如下。

（1）根据智能汽车的换道初始状态Sin和交通车的当前状态Stf，计算出合适的中转位置。

（2）根据换道车的换道初始状态Sin和中转位置的状态Scin，进行首次改进五次多项式规划，如图5所示。

图5 首次五次多项式轨迹规划

（3）到达中转位置后，根据换道车的中转状态Scin和换道目标状态Sfin进行第二次改进五次多项式规划，得到换道轨迹，如图6所示。

图6 双五次多项式轨迹规划

避障换道轨迹规划的具体流程图如图7所示。

图7 避障轨迹规划流程图

首次改进五次多项式规划的横向位移为1.8-2 m，略大于交通车的宽度，纵向位移和换道时间为待定系数，规划轨迹满足约束后会到达中转位置，此后两车不会再有碰撞的危险，第二次改进五次多项式规划等效为无障碍换道轨迹规划，两次规划的结果即为规划的轨迹。

双五次多项式规划的难点在于中转位置的选取。中转位置的选取须结合换道车的车速、交通车的车速、智能汽车与交通车辆之间的距离和智能汽车最终的位移等因素。综上可得，轨迹规划状态如式（11）所示，交通车的状态Stf如式（12）所示。

式中：vs为换道初始状态的车速；xc、yc和vc为换道中转状态的横向位移、纵向位移和速度；xf、yf和vf为换道目标状态的横向位移、纵向位移和速度。

式中：vtf为交通车C1的车速（小于vs）；xtf为换道车与交通车之间距离；atf为交通车的加速度。

当vtf=0时，即为障碍物静止时的避障换道。此时障碍物不再移动，为了避免发生碰撞，须xc＜xtf，所以当vtf=0时，完成换道需要的xtf，应大于vtf＞0时的xtf。

为尽快地完成换道过程，取vc略大于vs：

式中λ为换道加速因子，取值与车速成反比。

假设C0车和C1车经过t时间后两车位置相同，可得式（14）和式（15）：

式中vt为t时间后的交通车车速。

对式（15）求解得到Tmax：

式中：a为0.5倍的交通车的加速度；b为交通车的车速vtf与换道初始状态的车速vs之差；c为换道车与交通车之间距离xtf。

当vtf＞0时，使用微元法的思想进行分析，可得到如下等式：

式中T1为动态换道时间T的首项。

当vtf=0时，为避免发生碰撞，取T1=0.9Tmax，则

智能汽车进行第一阶段规划时，对于待定的中转状态的纵向位移xc、速度vc和换道时间T，取纵向位移xc如式（22）所示，速度vc如式（13）所示，换道时间T如式（24）所示。

式中Δt=0.1 s。

3 试验仿真

设定不同的工况进行仿真和实车试验，验证本文中所提算法的合理性。使用双五次多项式算法规划换道轨迹，并利用汽车动力学仿真软件CarSim对换道轨迹进行轨迹跟踪，对规划得到的规划轨迹和轨迹跟踪得到的实际轨迹性能进行对比，验证规划轨迹的性能，换道相关参数如表1所示。

表1 换道相关参数

3.1 无障碍换道仿真

对于无障碍换道，根据车辆的运动学特性，在换道起始时刻和结束时刻换道车的横向、纵向加速度均为0，取起始状态为（0，14，0，0，0，0），最终状态为（100，14，0，3.75，0，0）。

使用改进的五次多项式规划算法进行仿真试验，求解得到系数矩阵：

得到的无障碍换道轨迹参数曲线如图8所示。

从图8中可以看出，换道轨迹平滑，横向速度峰值小，换道平稳性较好。该算法在横向、纵向加速度方面的极值都较低，满足约束，曲线也更加平滑。在加速度变化率和曲率方面，曲线波动范围较小，证明该换道轨迹的舒适性较好。除此之外，整个换道规划的时间约为8 ms，也满足了高实时性的要求。

图8 无障碍换道轨迹参数

3.2 避障换道仿真

对于避障换道，交通情况如图4所示。智能汽车的换道场景如图9所示，图中的红色虚线为CarSim换道场景中规划的换道轨迹，红色车辆为换道车，白色车辆为交通车。

图9 双五次换道轨迹跟踪场景图

（1）前车车速为非匀速行驶时的轨迹规划

设定换道车起始时刻的速度为51 km/h，两车之间的距离为30 m，前方交通车车速为43 km/h，交通车的加速度为-2 m/s2。首次五次多项式规划求解得到系数矩阵分别为

第二次求解得到系数矩阵分别为

得到的仿真结果如图10所示。

图10 交通车变速时的换道轨迹参数

从图10（a）和图10（b）中可以看出，当前方交通车的速度发生变化时，中转位置在换道轨迹的后半段，且该条轨迹的跟踪精度高。在图10（c）中，轨迹的横向速度曲线峰值约为1.0 m/s。由图10（d）和图10（e）可知在轨迹的加速度方面，横向加速度和纵向加速度满足加速度约束，波动范围较低，故驾驶稳定性较高。由图10（f）可知在3.4 s时完成首次五次多项式规划，此时两车间距约为8.5 m，不存在碰撞风险。此后第二次五次多项式规划时，两车在纵向方面没有交集，故换道过程不存在碰撞风险。

（2）换道车高速行驶时的轨迹规划

设定换道车起始时刻的速度约为70 km/h，两车之间的距离为20 m，前方交通车车速约为50 km/h，另增加了与文献［18］中Chen Long等人的3⁃D Bezier规划轨迹在横向、纵向加速度方面的对比，得到的仿真结果如图11所示。

图11 高速情况的轨迹规划

从图11（a）中可以看出，轨迹跟踪效果好，精度高。图11（b）表明车辆能及时跟踪到目标速度并保持稳定。在图11（c）中，换道车辆的横向速度变化曲线的峰值小于1.5 m/s。由图11（d）可知，双五次多项式的换道横向加速度和轨迹跟踪得到的横向加速度的峰值均明显低于3⁃DBezier的峰值，相比之下驾驶稳定性较高。由图11（e）可知，换道前段的轨迹跟踪的换道纵向加速度较低，在换道后段纵向加速度波动较大，可以调节轨迹跟踪的相关参数避免波动发生，且此时两车在纵向已无交集，故不存在危险。由图11（f）可知，在2.73 s时完成首次五次多项式规划，此时两车间距约为12 m，不存在碰撞风险。此后第二次五次多项式规划时，两车在纵向方面没有交集，故换道过程不存在碰撞风险。

（3）换道车低速行驶时的轨迹规划

设定换道车起始时刻的速度为36 km/h，两车之间的距离为20 m，前方交通车车速为30 km/h，另增加了与文献［18］中Chen Long等人的3⁃DBezier规划轨迹在横向、纵向加速度方面的对比，得到的仿真结果如图12所示。

图12 低速情况下的轨迹规划

从图12（a）中可以看出，跟踪轨迹在整体趋势下遵循参考的规划轨迹，精度高。图12（b）表明，车辆能及时跟踪到目标速度并保持稳定。在图12（c）中，轨迹的横向速度曲线峰值小于1.0 m/s。由图12（d）和图12（e）可知，在轨迹的加速度方面，双五次多项式规划的加速度和轨迹跟踪得到的加速度的峰值均明显低于3⁃D Bezier规划得到的峰值，故驾驶稳定性较高。虽然延长了换道时间，但提高了换道舒适性。由图12（f）可知，在4 s时完成首次五次多项式规划，此时两车间距约为7 m，不存在碰撞风险。此后第二次五次多项式规划时，两车在纵向方面没有交集，故换道过程不存在碰撞风险。

（4）不同的前车距离和前车车速时的轨迹规划

设定换道车以约70 km/h的速度行驶，设定不同的前车距离xtf和车速vtf，并对规划得到的轨迹进行跟踪，如图13和图14所示。

在图13中，设定两车距离分别为15、20和25 m，前车的速度为50 km/h。图13（a）表明，使用该算法规划的轨迹合理。随着两车之间的距离改变，规划的不同轨迹也都可以被跟踪，偏差也都较小。由图13（b）可知，完成首次五次多项式规划时两车间距均在4 m以上，可以避免发生碰撞。

图13 不同前车距离时的换道轨迹跟踪

在图14中，前车的车速分别设定为30、40、50和0 km/h，初始时刻两车的距离分别为20、20、20和50 m。图14（a）表明，利用该算法规划的轨迹是可行的。规划得到的每条参考轨迹都能被高精度跟踪。由图14（b）可知，完成首次五次多项式规划时两车间距均在5 m以上，可以避免发生碰撞。

图14 不同前车车速时的换道轨迹跟踪

3.3 实车换道试验

将该算法应用于实际车辆的换道，交通情况如图15所示。

图15 换道交通情况

设定交通车静止，换道车也由静止开始换道，两车之间的距离为30 m，进行换道轨迹规划并对规划得到的轨迹进行跟踪，如图16所示。

图16 换道轨迹跟踪

从图16（a）中可以看出，跟踪轨迹在整体趋势下遵循参考的规划轨迹，规划的轨迹可跟踪性高。图16（b）表明，实际车辆的速度整体上可以跟踪上规划速度的变化趋势。在图16（c）中，轨迹的横向速度曲线峰值小于1.0 m/s。由图16（d）和图16（e）可知在轨迹的加速度方面，双五次多项式规划的横向、纵向加速度均满足舒适性约束。轨迹跟踪时除纵向加速度在从静止开始运动时瞬时值偏大外，其他时刻和平均值均符合约束。此外车辆在运动过程中与交通车的距离均在3 m以上。

4 结论

本文中以智能汽车换道轨迹规划研究为前提，对五次多项式规划算法进行了改进，最后提出了基于双五次多项式理论的智能汽车换道轨迹规划算法。该算法的特点如下。

（1）动态规划换道时间，使换道轨迹满足舒适性约束，提高了换道过程中的舒适性。

（2）引入中转位置并进行两次改进的五次多项式规划，避免有交通车辆时存在的碰撞危险，提高安全性。将中转点的状态选择与换道车和交通车的状态相结合，确保了中转位置的合理性。

（3）对算法程序进行优化，增强算法的实时性，可以快速地得到一条安全并且舒适度较高的换道轨迹曲线。

试验部分设计了包括前车变速行驶、换道车高速行驶、换道车低速行驶等多种工况的仿真试验和交通车静止时的实车换道试验，其中规划仿真与实车试验的结果表明了双五次多项式轨迹规划算法在各种工况下都可以成功规划出舒适的换道轨迹，并且在轨迹性能和运行时间方面都进行了优化，提高了换道过程中的安全性并增加了换道的实时性。轨迹跟踪的试验结果验证了该算法规划得到的轨迹的合理性，也证明该轨迹的可追踪性较高。综上，本文中提出的轨迹规划算法具有一定的实际应用价值。