汽车垂直泊车路径规划与路径跟踪研究*

高 强，陆 洲，段晨东，徐 婷

（1.长安大学汽车学院，西安 710064；2.长安大学电子与控制工程学院，西安 710064）

前言

高级驾驶辅助系统（advanced driving assistant system，ADAS）是当前汽车领域 热门的研究方向。ADAS系统通过车载传感器感知周围环境和汽车信息，进行分析和处理后，实现汽车定速巡航、车道保持和碰撞预警等功能［1］。自动泊车系统（automatic parking system，APS）是ADAS的组成部分，是智能汽车重要的研究内容之一。APS能够自动寻找停车位并泊入，有效减小驾驶员在泊车过程中的紧张程度，降低新手对狭小车位的泊车难度，减少剐蹭事故的发生［2］。国内外学者对自动泊车技术进行了多方面的研究［3-9］。

城市中垂直车位比较常见。当前垂直自动泊车技术的研究大多基于汽车初始位置航向角为零的情况（理想状况），没有考虑初始位置航向角误差对泊车的影响。在实际自动泊车过程中，初始位置航向角通常不会为零（即相对理想状态存在误差），此时如按零初始位置航向角进行路径规划和泊车，会造成汽车实际路径与规划路径存在较大偏差，从而在泊车中造成剐蹭或泊车失败等问题。针对上述不足，本文中研究了汽车初始位置航向角不为零时，垂直泊车路径规划与路径跟踪问题。首先对汽车初始位置航向角不为零时的泊车路径进行规划，使用四次样条函数改进规划路径；然后针对常用的预瞄误差前馈方法在路径跟踪中有时存在较大误差的问题，设计了预瞄误差前馈和航向角反馈相结合的控制方法，对期望路径进行跟踪；通过Simulink/CarSim联合仿真，研究了所设计垂直泊车算法的有效性；最后通过实车试验对该算法进行了验证。

1 研究方法

1.1 自动泊车系统工作流程

自动泊车系统工作流程如图1所示。驾驶员开启自动泊车功能后，APS系统对汽车进行控制，汽车向前行驶，同时车载环视摄像头对汽车周围环境进行感知。当检测到停车位时，APS对当前车位进行路径规划，然后控制汽车进行路径跟踪，直到汽车成功泊入停车位。泊车完成后转向盘回正并挂驻车挡，自动泊车系统关闭。

图1 自动泊车系统工作流程图

1.2 汽车运动学模型

汽车轮廓形状直接影响泊车成功率。由于实际汽车的轮廓形状较为复杂且难以准确建模，这里在给予一定裕度的情况下使用矩形替代汽车模型，其长度和宽度分别为汽车的最大长度和最大宽度，简化后的汽车模型如图2所示。在本文计算、仿真和实车试验中，汽车主要参数如表1所示。

图2 简化汽车模型

表1 汽车主要参数表

选取APS系统开始工作时刻后轮中心点为汽车参考点。在低速泊车工况下，根据阿克曼转向原理，将汽车视为平面刚体，即只具有x方向、y方向和横摆3个自由度。汽车在坐标系的坐标为(x，y)，航向角为ψ，汽车运动学方程为

式中：v为车速；δf为等效前轮转角。

1.3 垂直泊车基础路径规划策略

假设汽车垂直泊车时初始位置航向角为θ，以汽车前进方向为X轴，自动泊车系统开始工作时刻汽车后轴中心为原点O，原点左侧垂直方向为Y轴建立坐标系，如图3所示。通过摄像头模块探测得到垂直车位的两个顶点坐标为(xa，ya)和(xb，yb)，可得汽车相对于车位的初始位置航向角θ为

图3 垂直泊车第1次停车点示意图

如图3定义初始位置航向角向上为正，向下为负。进行泊车路径规划时要确定以下几个关键点的坐标。

（1）泊车起始点S1坐标。假设汽车行驶到S1点时，以最小转向半径R倒车，考虑车位右顶点(xb，yb)的约束，汽车在S2点第1次停车，驶过的圆弧路径为

根据汽车运动几何关系，易证车身M点在倒车过程中与车位右顶点(xb，yb)距离最近。设安全阈值LS1=0.1 m，可得点O1(xO1，yO1)的坐标为

从而求得起始点S1的坐标为

图4 旋转坐标系后的垂直泊车工况

式中LS2=0.1 m，为设置的S2点安全阈值。同时为保证泊车终止点位姿良好，应使汽车最终停车点的航向角在OX1Y1坐标系下接近90°，如图5所示。若汽车沿规划路径行驶中满足上述条件，则可实现一步泊车入库。

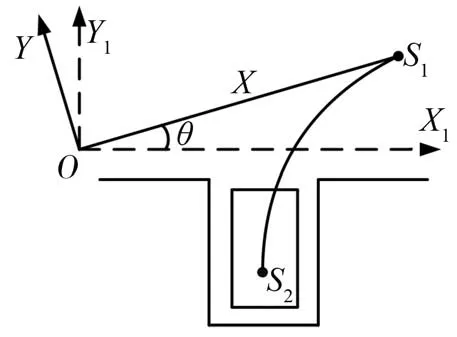
图5 垂直泊车一步泊车入库

（2）停车点S2坐标。若汽车行驶到S2点时车身左后顶点Nd不满足式（5），则须多步入库，此时须进行下一步路径规划。汽车基于OX1Y1坐标系下航向角变化量如图6所示。

图6 多步泊车路径航向角变化

由图6几何关系可以求出：

汽车从路径点S1到路径点S2驶过的航向角ψ1为

根据求得的航向角ψ1，计算S2点的坐标为

（3）前进点S3坐标。接下来汽车应调整转向盘转角为零，沿着直线路径S2S3朝前行驶到S3点，最后再以最小转向半径R倒车入库，路径曲线为规划后多步泊车路径如图7所示。

图7 垂直泊车多步泊车入库

设直线段路径S2S3的长度为Lb，则根据几何关系可以求得

则S3点坐标为

汽车从路径点S3到路径点S4驶过的航向角ψ2为

根据ψ2的值可得路径的圆心坐标：

最后求得S4点坐标：

1.4 垂直泊车路径改进

当汽车行驶到S3点时，需要重新对路径进行规划。实际泊车过程中，由于存在传感器、执行器等多种误差，可能会导致汽车不能准确跟踪期望路径，那么基于最小转向半径的路径规划有可能导致路径跟踪失败（因需要的转向半径小于最小半径），进而造成泊车失败。为增加泊车算法的鲁棒性，同时减小汽车原地转向现象，本文中选用四次样条函数改进段路径，使其曲率连续并满足汽车转向约束。四次样条函数公式可表示为

根据规划路径起始点位置和航向角，可得

根据路径终止点位置和航向角，可得

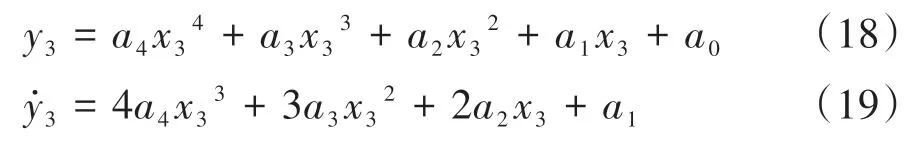
最后，确定障碍物约束，即在倒车过程中不能与障碍物发生刮蹭。选取一个约束点为中间点，可得

根据式（16）～式（20），可以得到一条唯一的四次样条曲线，该曲线即为规划的路径。在垂直泊车过程中为使得生成路径满足汽车转向半径约束，将S3的位置沿当前航向角方向延长一段距离Ld1，则延长后的样条函数起始点坐标为

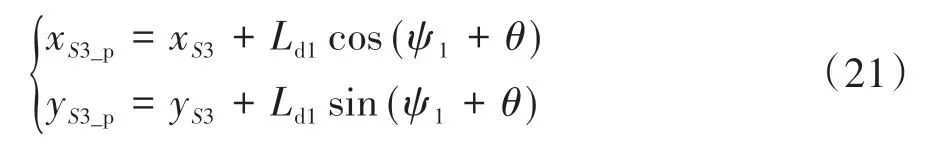
相应地将泊车终止点坐标S4向下延长一段距离Ld2，则延长后样条函数终止点坐标为

选取不同的中间点，会生成不同曲率的曲线，这里以考虑车位左端点约束时的S2点为参考点，并对其进行修正作为中间点：

式中Δs为修正值。根据式（21）～式（23），可以得到系数确定的四次样条函数曲线。

1.5 垂直泊车横向跟踪控制模块

自动泊车系统控制转向盘转角，使汽车在前进方向的垂向产生速度，从而使汽车沿已规划路径行驶称为横向控制，主要使用的算法有预瞄控制、PID控制、模糊控制、LQR和MPC控制等［3-7］。国外MacAdam提出了最优预瞄控制模型［8］。

国内郭孔辉院士提出了单点预瞄最优曲率模型［9］，其原理如图8所示。假设汽车以恒定速度v行驶，汽车跟踪的路径方程为f(t)，路径上点即为理想预瞄点。驾驶员根据前方路径点的信息，结合汽车自身运动状态，对汽车到达期望点的误差进行估计，计算一个最优圆弧路径，并根据圆弧曲率半径与转向盘转角的关系得到一个转向盘转角的期望输入。最优圆弧路径在实践中一般通过实车反复调试得到。若汽车后轴中心点的实际轨迹为y(t)，汽车侧向加速度为y，在较低行驶速度下，根据阿克曼转向原理，汽车轨迹曲率可视为与等效前轮转角成正比：

图8 最优预瞄曲率原理

式中：r为道路曲率半径；δf为等效前轮转角；R1为汽车转弯半径；i为转向系传动比。

此时汽车横向位置为y(t1)，设驾驶员预瞄距离为d，预瞄时间为T=d/v。经过一个预瞄时间T后，汽车横向位置变成y(t1+T)，对该式进行泰勒级数展开，忽略高阶项，保留其2阶项得

根据误差最小原则，驾驶员期望得到一条最优轨迹，使得汽车经过一段时间T后可以到达预期位置f(t1+T)。由式（24）～式（26）可以得到基于最优曲率的转向盘转角：

式中δsw为转向盘转角，且δsw=δfi。

根据控制需要，规划出来的汽车路径由一系列坐标点组成。在实际跟踪过程中，根据当前汽车位置，选择一个合理预瞄距离d，通过计算得到参考路径距预瞄点最近的点(xj，yj)与预瞄点(xd，yd)的距离，这段距离称之为预瞄误差e(j)。预瞄误差示意图如图9所示。由图可知，为使汽车实际行驶路径与期望路径误差最小，由式（27）可得预瞄误差与此时转向盘转角δe之间的传递函数：

图9 预瞄误差

式中j为预瞄点序号。

当前很多研究采用预瞄误差前馈控制方法对规划路径进行跟踪。由于跟踪中存在模型误差和环境干扰等因素，仅依靠预瞄误差前馈的控制方法有时难以保证精确的跟踪效果和良好的跟踪稳定性。考虑到实际泊车过程中，汽车航向角对路径跟踪效果影响较大，因此本文中增加汽车航向角反馈环节来同时对转向盘转角进行调节，即采用预瞄误差前馈加航向角反馈的控制方法对规划路径进行跟踪。

如图10所示，在某一时刻汽车位置为(xrk，yrk，ψrk)，路 径 上 距 离 汽 车 最 近 的 一 点 坐 标 为(xk，yk，ψk)，则汽车此时的航向角误差λerr定义为

图10 汽车航向角误差示意图

式中k为路径点序号。

采用PID算法减小航向角误差，调节转向盘转角。转向盘转角的PID控制表达式为

式中：kp、ki和kd分别为比例、积分、微分系数。考虑预瞄误差前馈，结合航向角反馈，则转向盘转角δsw为

整个泊车路径跟踪模块控制框架如图11所示。

图11 预瞄控制器框架图

2 仿真验证

基于Simulink/CarSim对所提出的泊车路径跟踪算法进行了联合仿真。首先在CarSim中根据目标参数建立了汽车模型和停车位场景，并导入Simulink。然后在Simulink中搭建了基于样条函数的路径规划模块，并建立了预瞄误差前馈加航向角反馈的跟踪控制模块，最后进行联合仿真。

对汽车初始位置航向角分别为5°、0°和-5°时自动垂直泊车系统路径规划及路径跟踪结果进行仿真，结果如图12～图14所示。

图12 初始位置航向角为5°的泊车仿真

图14 初始位置航向角为-5°的泊车仿真

从仿真结果可以看出，在汽车初始位置航向角分别为5°、0°和-5°时，路径规划模块都规划出了泊车路径。图12（a）和图13（a）泊车过程中，仅使用预瞄误差前馈控制方法时，对曲率不变的路径和跟踪效果良好。在对四次样条函数规划的路径进行跟踪时，由于曲率是变化的，航向角也随之改变，采用单一的预瞄误差前馈控制跟踪存在较大的滞后现象，跟踪效果较差，最大横向误差分别达到了25和20 cm，最终泊车姿态不太理想，偏角分别为7°和5°。而在加入了航向角反馈后（图12（b）、图13（b）），在曲率不变路径跟踪效果同样较好，而在曲率变化的路径，最大横向误差分别减小到6和5 cm，跟踪精度更高，跟踪响应速度快，且最终泊车姿态良好，偏角均小于5°。由图14（a）可以看出，在初始位置航向角为-5°时，由于曲率变化引起汽车航向角变化量较大，仅使用预瞄误差前馈的控制模块不能及时对汽车转向盘转角进行调整，导致汽车在跟踪时侧向偏差最大达到了40 cm（点P），最终泊车位置姿态角达到了35°，汽车轮廓线与车位轮廓线发生了剐蹭，泊车失败。由图14（b）可以看出，按本文方法加入了航向角反馈控制后，汽车转向盘调整及时，最大侧向误差点P的误差小于5 cm，汽车能够准确地跟踪规划路径，顺利泊入车位，且最终泊车姿态良好，偏角小于5°。

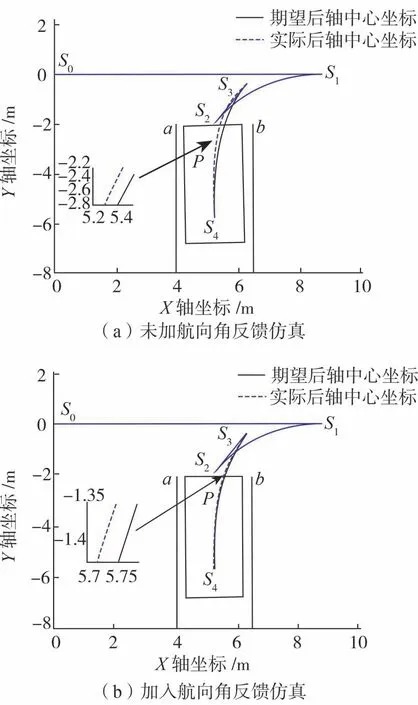
图13 初始位置航向角为0°的泊车仿真

因此，在泊车路径跟踪过程中，对于曲率不变路径，预瞄误差前馈控制就能较好地对路径进行跟踪，但对于曲率变化的路径，预瞄误差前馈控制跟踪误差变大且具有较大滞后现象。在预瞄误差前馈的基础上加入了航向角反馈控制后，对曲率不变和曲率变化路径都具有较好的跟踪效果，且最终泊车位姿良好。

3 垂直泊车路径规划与跟踪实车验证

3.1 试验平台

为了对本文中提出的垂直泊车路径规划和路径跟踪策略进行工程验证，利用一辆试验车进行了多组实车试验。试验车如图15所示，该车具有ETRS电子排挡和EPS电动助力转向系统，能够实现对转向盘转角、加速、制动踏板和挡位的自动控制。

图15 试验汽车示意图

汽车实车试验平台如图16所示，主要由以下部分组成：（1）感知系统：主要包括环视摄像头（检测停车位信息）和12个超声波雷达（实现避障）；（2）摄像头控制器：分析环视摄像头采集到的数据，以及汽车自身数据，得到停车位角点坐标；（3）泊车控制器（infineon TC233）：运行基于四次样条函数的路径规划算法，以及预瞄误差前馈加航向角反馈路径跟踪算法，输出转向盘转角信号、挡位、加速踏板和制动踏板信号；（4）CAN盒（VPN1630）：负责整车的CAN通信，在其配套软件CANoe上对整车报文进行解码和编制收发目标报文；（5）UDE联合调试器：负责将Hightec生成的可执行程序烧入控制器以及全局变量的观测和代码调试；（6）PC端（ThinkPad T470P）：进行数据分析、代码修改和变量监控；（7）供电模块：为控制器提供12 V稳定电压。

图16 汽车试验平台组成

3.2 试验算法和结果分析

航向角是实车试验中重要的参数，但它难以借助一般的车载传感器直接获得，本试验通过以下算法计算得到车辆航向角：

其中：

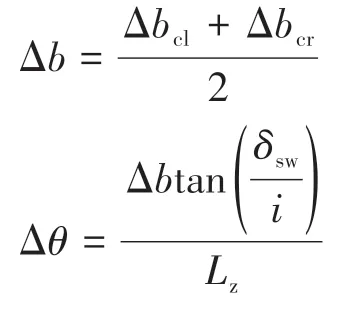
式中：（x，y)为汽车后轴中心坐标；Δb为等效后轴位移增量；Δθ为航向角增量；Δbcl、Δbcr分别为左后轮和右后轮位移增量，可以通过轮速脉冲和车轮半径求得。

分别对初始位置航向角为10°、5°、0°和-5°的情况进行了试验。期望后轴中心坐标通过UDE联合调试器从泊车控制器中读出，实际后轴中心坐标从汽车惯导数据获得，并通过CAN总线由CANoe处理读出，最后在MATLAB中绘图。试验结果如图17～图20所示。

图17 初始位置航向角10°的泊车试验

图18 初始位置航向角5°的泊车试验

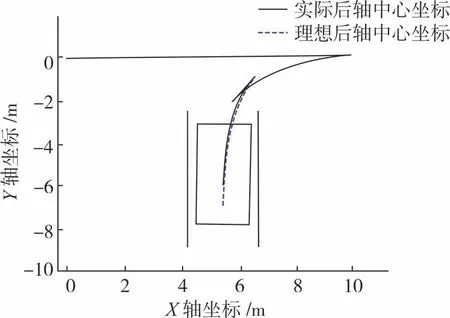
图19 初始位置航向角0°的泊车试验

图20 初始位置航向角-5°的泊车试验

由试验结果可以看出，在初始位置航向角为10°、5°、0°和-5°的情况下，汽车均能顺利规划并跟踪泊车路径，泊入车位，跟踪误差小于5 cm，最终停车点位姿角小5°，跟踪精度较高，控制效果较好。说明本文中提出的垂直泊车路径规划方法和控制策略能够较好地实现实际交通环境中的垂直泊车问题，具有较好的应用前景。

4 结论

对具有初始位置航向角的泊车工况进行了路径规划，并结合四次样条函数对路径进行了改进。设计了一种预瞄误差前馈加航向角反馈的跟踪控制算法，在规划路径曲率不变和变化的情况下都能够较好地跟踪规划路径，跟踪精度高，鲁棒性强。基于Simulink/CarSim进行了联合仿真，仿真结果表明在具有一定初始航向角的情况下，路径规划模块均能规划出一条可行路径，路径跟踪控制模块可以对其进行精准跟踪。实车试验也验证了本文提出垂直泊车路径规划和路径跟踪方法的有效性。