智能网联混合动力车辆速度规划的多目标协同控制研究*

解少博，罗慧冉，张乾坤，张康康

（长安大学汽车学院，西安 710064）

前言

开发智能网联新能源汽车是实现节能减排、提升车辆性能和促进汽车产业转型升级的必然趋势，已成为全球汽车厂商和科研机构关注的热点。同时，通信技术的高速发展使得V2X技术不断演进，车辆与道路以及行驶环境之间的信息交互不断增强，也在客观上加快了车辆智能化的步伐。

在智能网联汽车行驶过程中，基于V2X获取的道路交通信息对车速进行实时规划是提高行驶安全性、机动性、经济性和通行效率的必然要求。行驶速度首先影响到车辆的机动性。同时，速度需求决定了功率需求，即要求动力系统进行响应，而智能网联混合动力汽车具有电池和发动机等多个能量源，为提高经济性，应该合理地进行功率分配，即要求进行能量分配策略的设计。与此同时，能量分配中电池输出功率的大小又会对其寿命造成影响，过多地使用电池的电能尽管可以提升经济性（行驶单位里程的电池电能成本要远小于燃料成本），但会加速电池的老化，从而增加电池老化成本。另外，车速也会影响到乘坐的舒适性，如波动式的速度会严重影响舒适性。由此可知，智能网联混合动力汽车的安全性、舒适性、机动性、能量分配和电池老化是相互影响的，需要对诸多目标协同优化与控制才能全面提升车辆的性能。

现有研究多从经济性驾驶的角度来优化行驶速度。如文献［1］中基于庞特里亚金极小值原理（PMP）制定最佳的速度轨迹以减少油耗。文献［2］中针对给定行驶路线，采用动态规划（DP）算法优化车辆从起点到终点的经济车速。然而这种基于全局优化进行的速度规划显著缺点是不具有实时性。另外，针对坡道［3］、弯道［4］和交通信号灯［5］等实际场景的车速规划问题也被广泛研究。

对混合动力汽车而言，实现多种能量源之间功率的优化分配对于提升能耗经济性尤为重要。为此，研究人员提出了多种能量分配策略。如基于规则的策略［6］，基于动态规划（DP）［7］和庞特里亚金极小值原理（PMP）［8］等全局优化策略、可以实时应用的等效能耗最小化策略（ECMS）［9］，以及通过在滚动时域内实施DP等优化算法而形成的模型预测控制（MPC）策略［10］。此外，基于数据驱动的学习型方法［11］也在能量分配中得到了越来越多的关注。

针对智能网联汽车的速度规划已展开了相关研究［12］，但针对混合动力汽车的协同考虑安全性、经济性、机动性、能量管理和电池老化的多目标实时控制问题，尚需深入分析。

基于上述考虑，本文中以智能网联混合动力客车在弯道行驶场景为例进行速度的实时规划，利用模型预测控制形成多目标优化问题，并基于动态规划算法对滚动空间域的优化问题进行求解，从而实现实时的车速规划和功率分配，同时讨论了考虑电池老化与否以及机动性和舒适性选择不同权重时对结果的影响。

1 智能网联混合动力汽车系统建模

1.1 动力系统结构

本文中以一款智能网联混合动力客车为例展开研究，其动力系统部件主要包括发动机、ISG电机、动力电池和轮边驱动电机等［13］。其中，发动机与ISG电机同轴相连，组成EGU单元，驱动电机通过轮边减速器与车轮连接。车辆动力系统结构如图1所示，整车主要参数见表1。

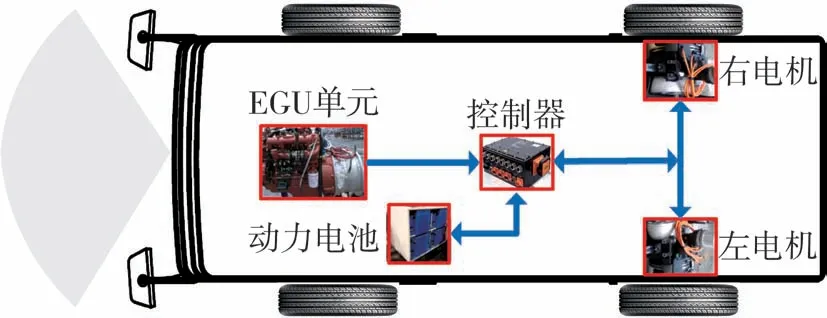
图1 智能网联混合动力客车动力系统结构示意图

表1 整车参数

1.2 动力系统数学模型

（1）发动机和ISG电机模型

组成EGU的发动机为一款排量为4.2 L的天然气发动机，标定功率为88 kW，最高转速为2 800 r/min，最大转矩为380 N·m，其能耗Map如图2所示。

图2 发动机能耗图

ISG电机为永磁同步电机，通过法兰与发动机直接连接，其额定和峰值功率分别为80和130 kW，对应的额定和峰值转矩分别为350和600 N·m，最高转速为6 000 r/min，效率特性如图3所示。

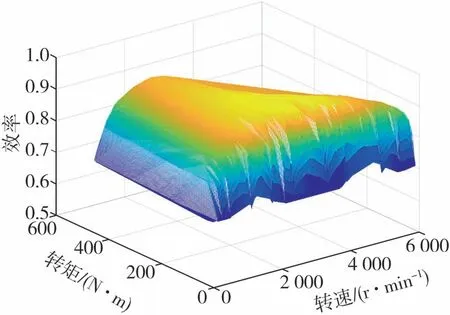
图3 ISG电机效率特性

综合发动机和ISG电机的能耗效率可以得到EGU等燃气消耗率曲线，如图4所示，其中红色虚线为最佳燃气消耗率曲线。

图4 EGU等燃气消耗率曲线

（2）驱动电机模型

两个轮边驱动电机为永磁同步电机，额定和峰值转速分别为2 500和6 000 r/min，额定和峰值转矩分别为320和650 N·m，对应的额定和峰值功率分别为85和150 kW，其效率特性如图5所示。

图5 驱动电机效率特性

1.3 电池模型

（1）电池电路模型

电池由168只磷酸铁锂电池单体串联成组，单体电压为3.2 V，总电压为537.6 V，标称容量为100 A·h。电池内阻和开路电压作为电池核电状态（SOC）的函数［14］，单体电池的特性如图6所示。

图6 电池单体开路电压和内阻随SOC的变化

电池组存在如下功率平衡关系：

式中：Pbat为电池的总功耗；Pb为电池负载端的功率；Pl为电池的功率损耗。

由功率关系可得电池的电流为

式中：Uoc为开路电压；Rb为等效内阻。

（2）电池老化模型

使用半经验电池老化模型［15］表征动力电池单体的容量损失比例，如式（3）所示。

式中：Qloss为电池容量损失百分比；B为指数前因子，取值31 630；c为充放电倍率；Ea为活化能；R为气体常数，取值8.314；T为电池工作环境温度；z为指数因子，取值0.55；Ah为安时吞吐量。

当电池容量损失达到标称容量的20%时，认为电池达到寿命终止状态（EOL）［16］。当处于标准工况（环境温度为25℃，充放电倍率为0.3C），动力电池到达寿命终止状态时的总安时吞吐量Γnom可表示为

式中Inom为电池在标准试验工况的充放电电流值。

实际行驶工况下，动力电池达到寿命终止状态时总安时吞吐量γ可表示为

式中Ib为电池在实际工况的充放电电流值。

引入电池衰减因子σ［17］表示电池在实际工况相对于标准工况下的老化程度，计算公式为

同时，本文假定动力电池的热管理系统使电池温度维持在恒定温度25℃。

1.4 整车动力学模型

车辆在弯道行驶时，轮胎的侧偏现象将使滚动阻力增加，附加的曲线行驶阻力如式（7）所示［18］。

式中：Fc为曲线行驶阻力；G为车辆重力；v为车速；Rc为弯道半径；lH为总质心到后轴的距离；lV为总质心到前轴的距离；l为轴距；αH为后轮侧偏角；αV为前轮侧偏角。

根据整车纵向行驶过程中的驱动力和阻力平衡关系，得到如下动力学方程：

式中：Ttq为驱动轮需求转矩；i0为轮边减速器减速比；ηT为传动效率；r为车轮滚动半径；m为车辆质量；g为重力加速度；f为滚动阻力系数；Cd为空气阻力系数；A为迎风面积；δ为旋转质量转换系数。

2 速度规划问题的形成

智能网联车辆在行驶过程中尤其在弯道等特殊场景中，对车速进行规划首先考虑侧向安全性，防止侧滑、侧翻等事故的发生，同时还要考虑能耗经济性、机动性、舒适性和电池老化等多重目标。对于智能网联混合动力城市客车，本文中假设其行驶在自由交通流环境中，且车辆可以通过全球定位系统（GPS）进行实时定位，利用配备的车载单元（OBU）与路侧单元（RSU）进行通信，以获取当前路段的弯道半径信息。

2.1 模型预测控制

为满足实时控制要求，采用模型预测控制（MPC）对车辆未来有限空间域内的车速进行规划。以预测空间域内的能耗成本、电池老化成本、行驶机动性成本和乘坐舒适性成本的加权和最小化为目标，在弯道安全性、动力系统和电池系统的约束条件下，进行多目标实时优化，从而得到滚动空间域内的车速规划和能量分配关系，其原理架构如图7所示，具体步骤分为以下4步。

图7 多目标速度规划架构

（1）模型预测：设预测空间长度为Sp，将Sp平均分割为n段，并设第i个路段单元为Sp，i。假设车辆在第i个路段内为匀加速运动，则基于所有可行加速度值（由实际行驶数据统计得出其取值范围）可以得到预测空间域内对应的速度谱。

（2）滚动优化：在滚动空间域中，基于（1）中得到的所有可能速度谱使用动态规划进行功率分配的优化，并通过对比总成本大小选择出预测空间内的最优速度轨迹。

（3）反馈校正：选择预测空间域内第1个路段单元的最优控制量（加速度a和EGU输出功率序列PEGU）分配给车辆，更新车辆动力学方程，进入下一个滚动空间域并重新预测该滚动空间域中车辆的运行状态，修正上个滚动空间域的优化控制量，完成反馈校正。

（4）重复上述过程直至行程结束。

2.2 目标函数

以预测空间域内的经济性综合成本（能耗成本与电池老化成本）、机动性和舒适性的加权成本之和最小化构建目标函数，即

式中：Jeco为离散空间域上不同速度谱对应的经济性成本；treal和texpect分别为离散空间域内每一个路段单元的实际行驶时间和期望行驶时间；ai为第i个离散路段单元的加速度；Sp为预测空间域长度；s表示离散距离；λ和β分别为机动性和舒适性权重因子。

经济性成本Jeco包括消耗的天然气和电能成本与电池老化成本，其表达式为

式中：cf为天然气单价，取3.7元/m3；mf为天然气消耗率；ce为单位电价，取0.8元（/kW·h）；ψ为电池购置成本，电池单价取1 900元（/kW·h）。

控制变量u和状态变量x分别为

式中：a为加速度；PEGU为EGU输出功率；v为行驶车速。

目标函数的最优解为车辆的加速度和EGU的功率序列：

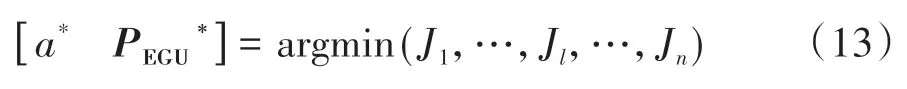
式中Jl表示预测空间域的第l个速度谱对应的总成本。

由加速度可以得到规划的速度序列，由EGU功率序列可以得到电池和EGU的功率分配关系。

3 问题的求解

3.1 预测空间域速度谱

实施MPC需要对预测空间域内车辆的行驶状态进行预测。设预测空间域的长度为Sp，将该长度进行离散并设第i个离散的路段单元长度为Sp，i。假设在每个离散域内，车辆作匀加速运动，其加速度为ai，j，则在一个离散域内的车速存在如下关系：

式中：vi-1和vi分别为该离散域内的起点和终点的速度；ai，j为第i段路段上第j个可能加速度值。

对于在弯道行驶的车辆，由于曲线行驶阻力系数随着侧向加速度的增大而上升，呈非线性关系。当侧向加速度超过0.4g，轮胎呈现非线性特性［18］，可能导致车辆失稳，因此速度需满足如下约束：

但实际行车过程中，由于各种扰动的存在，以临界车速作为最大过弯车速不足以保障车辆的行驶安全和乘客的舒适性，为提升车辆过弯时的横向稳定性和乘坐舒适性，将上式乘以一个收缩系数从而得到：

式中：vmax为弯道最大行驶车速；φsafe为收缩系数，取值0.5。

因此，车辆过弯时的车速可表示为

3.2 动态规划

由于本文中研究对象为混合动力客车，动力电池在充放电过程中总体呈电量维持状态，故在实施MPC策略时，将参考SOC设置为定值。同时，在MPC预测空间域内，将空间域速度谱转化为时域速度谱，在时域内采用动态规划（DP）算法进行优化控制，以此求得有限空间域内的全局最优解。其数值离散形式表达如下：

式中：Ck为第k步的最小成本；xh为第h个SOC离散点的值；up为第p个控制输入；Uk为控制变量的集合；g(∙)为当前步的综合成本；T为车辆在预测空间域内行驶所需的时间；f(∙)为系统状态方程；φ为惩罚函数，用于保证预测空间域SOC末值维持在参考SOC附近，其中系数ω取为105，SOC参考值SOCref取为0.6。

本文中将状态变量SOC等间隔离散为10个点，得到SOC=[SOCmin：△SOC：SOCmax]。

由电池模型可得

式中：Qb为电池容量；SOC为SOC的变化率。

SOC的状态转移方程可表达为

变量的约束条件为

式中：Pe、PEGU、Pb分别为发动机、EGU、动力电池的输出功率；下角标min和max分别表示变量的最小和最大值；SOC0和SOCend分别为滚动空间域内SOC初始值和末值。

4 结果与分析

以车辆在不同弯道半径的连续弯道行驶场景为例进行多目标协同的车速规划研究，同时为了评估不同目标及其权重对结果的影响，讨论目标函数考虑电池老化与否，以及改变期望行驶时间、机动性权重因子和舒适性权重系数对结果的影响。计算过程中，为凸显弯道行驶时对安全性的考虑，假设道路的弯道半径Rc在200-300 m范围变化，如图8所示，路段总长约3 km。在计算过程中，Sp取200 m，Sp，i取100 m。基于对实车在市区工况行驶数据的统计分析，车辆加速度ai，j的范围取为［-1.0 1.0］m·s-2，离散步长取0.1 m·s-2。根据式（16）对侧向加速度ay进行约束，最终得到其取值区间为［0 1.0］m·s-2。另外，车速的初始值设为36 km·h-1。综合成本定义为能耗成本（电耗与气耗成本两项之和）与电池老化成本之和。本文的仿真计算是基于MATLAB软件且在2.6 GHz CPU和8 GB内存的笔记本电脑上进行的。

图8 弯道半径随行程的变化

4.1 目标函数考虑电池老化与否的结果分析

当不考虑电池老化的影响时，此时目标函数中经济性成本只考虑电能和天然气消耗成本，其表达式为

计算结果如表2所示，可以看到，考虑电池老化的策略将电池老化成本作为一项优化指标，其老化成本相对不考虑老化时减少25.8%。原因主要是当目标函数考虑电池老化成本后，可有效抑制动力电池大电流充放电和频繁充放电现象，从而降低电池老化成本，使综合成本比不考虑电池老化时要低。可以看到，考虑电池老化时在不影响整车动力性和机动性的情况下（见图9的速度谱），其综合成本相对于未考虑电池老化模型时降低2.3%，车辆的经济性能得以提升。两种情况下，动力电池SOC均在0.6附近波动，符合预期要求，其变化曲线如图10所示。

表2 目标函数考虑电池老化与否的结果对比

图9 考虑电池老化与否的车速谱

图10 考虑电池老化与否的SOC曲线

4.2 不同期望行驶时间的结果分析

改变每个路段单元上的期望行驶时间texpect，即改变行驶100 m的期望时间。这里使其在5-8 s，分5种情况进行讨论，结果见表3。可以看到，当期望时间越大，优化过程中将选择越低的车速，使得车辆的机动性减弱。同时随着期望时间的不断增大，平均车速不断减小，使得需求功率减小，从而在整体上使能量消耗成本（气耗与电耗）减小，电池衰减成本也相应地降低，使得综合成本不断减小。例外的情形是当期望时间取6.5 s时，由于受其它目标的影响，使得电耗量突然增大，对应的气耗量减小以及电池老化成本增大。折中选择7 s作为后文的期望行驶时间。

表3 不同期望行驶时间的结果对比

SOC和车速变化曲线如图11和图12所示，从图中可以看出，不同期望行驶时间SOC轨迹各有差异，但均能保持在0.6附近波动。

图11 不同texpect对应的SOC曲线

图12 不同texpect对应的速度谱

4.3 不同机动性权重因子的结果分析

改变机动性权重因子λ，使其值从0.1增大至10共计5种情况进行讨论，结果如表4所示，对应的SOC和速度变化如图13和图14所示。由结果可知，在一定范围内（λ从0.1增大至1），随着λ的增大即车辆机动性的提升，平均车速升高，功率需求增大，同时受电池老化成本这一因素的影响，综合成本也随之升高，但继续增大时车速基本不变，这是由于仿真过程中期望行驶时间设为7 s，权重λ较小时，实际行驶时间较长，平均车速较低；随着λ的增大，实际行驶时间逐渐接近期望行驶时间，车速基本趋于稳定。

图13 不同λ对应的SOC曲线

图14 不同λ对应的速度谱

表4 不同机动性权重因子的结果对比

4.4 不同舒适性权重因子的结果分析

改变舒适性权重因子β，使其值从0.5增大至40共计5种情况进行讨论，结果如表5所示，对应的车速谱如图15所示。当β取0.5时，车速波动明显，出现频繁的加速-制动现象，用电成本较高，使得综合成本相对β=3.5时较小。当β从3.5逐渐增大至40时，总体来看车速波动明显减小，即舒适性提升；同时可以看出，β在这一范围内，电耗先增大后减小，而对应的气耗近似呈现先减小后增大的趋势；受多重目标的相互影响，综合成本呈逐渐下降趋势。不同β对应的SOC如图16所示。

图16 不同β对应的SOC曲线

表5 不同舒适性权重因子的结果对比

图15 不同β对应的车速谱

5 结论

本文中针对一款智能网联混合动力客车在弯道场景的速度实时规划问题，提出考虑车辆能耗经济性、机动性、舒适性和电池老化等多重目标的协同控制方法，并基于模型预测控制在滚动空间域中优化车速和功率分配，得到以下结论。

（1）与目标函数不考虑电池老化的协同控制策略相比，考虑电池老化能够在保证车辆动力性和机动性的同时，使电池老化成本降低25.8%，使综合成本降低2.3%。

（2）随着期望行驶时间的减小，平均行驶车速随之升高，但综合成本也逐渐增加。

（3）在一定范围内提高机动性权重因子能够提高车速，缩短行驶时间，但综合成本有所上升。实际应用过程中，需要权衡经济性与机动性这对矛盾因素，选择合适的权重因子。

（4）舒适性权重因子的增大能够减小车速波动，同时降低综合成本。

考虑到纵、侧向加速度与车辆操稳性和舒适性的定量关系模型十分复杂，本文未能建立其精确模型，后续将对这一点进行深入研究。