基于参考向量场的车辆队列二维跟踪控制算法*

刘 阳，宗长富，郑宏宇，韩小健，张 东，郭中阳

（1.吉林大学，汽车仿真与控制国家重点实验室，长春 130022；2.南洋理工大学机械与宇航工程学院，新加坡 639798；3.江苏超力电器有限公司，丹阳 212321）

前言

智能网联汽车利用感知和通信设备，能够实现车辆的智能决策、规划跟踪和执行控制等功能。多辆智能网联汽车排成一列，通过自适应调整车辆的速度与横摆角，能够有效改善车辆的经济性、安全性，提高道路通行效率。目前车辆队列协同控制的研究从一维场景逐渐拓展至二维场景，原本的单车道行驶工况变为多车道，且无法忽视车辆行驶过程的纵横向耦合问题。

当车辆队列的应用场景进入二维后，所有的车辆节点均须同时实现纵向的间距保持和横向的路径跟踪功能。目前，已有学者针对车辆队列在二维场景的协同控制方法进行了研究，并将车辆队列二维场景的协同控制归纳为两点主要内容：产生跟随车的特定参考轨迹和设计用于车辆进行特定轨迹跟踪的控制系统［1］。本文中将主要对后者进行研究与分析。

跟随车辆轨迹跟踪的生成方法主要包含两类：直接跟车法［2-3］和跟踪领航车行驶路径的跟踪控制方法［4-5］。与直接跟车法相比，将领航车的参考路径或行驶路径作为队列中其它车辆节点的参考路径时，能够实现车辆节点间横向跟踪解耦，避免了横向跟踪误差随着队列系统的传递而增加。

已有特定间距策略与期望参考轨迹时，车辆队列的分布式运动控制器须同时进行纵向与横向的跟踪控制。Rajesh等在考虑车辆非线性动力学特性、队列稳定性的条件下，实现高速工况下的跟踪控制，并在通信受限的环境下完成分离与合并工况［6］。Papadimitriou等开发了一种基于前车横向位置的队列内车辆节点横向跟踪控制器，提出在多车辆队列系统中，需要车间通信技术来避免多队列系统横向误差传播的放大效应，并利用乘用车和商用车试验与仿真数据证明了算法的有效性［7］。在进一步的研究中分析了在车间通信受限环境对轨迹跟踪与纵向间距保持的影响［8］。Awawdeh等基于“预瞄距离”的策略，考虑车辆的运动学模型、轨迹曲率和允许的距离误差条件下生成了跟随车的参考轨迹并进行横向跟踪控制，仿真结果表明，该方法能够从根本上减少队列在横向及纵向的波动效应［9］。Khatir等针对车辆队列在二维场景中的控制，将队形策略总结为“直线队形”和“侧面队形”两种，以牵引力和车轮转角为控制变量对车辆节点进行分布式控制，并实现了预设的特定任务［10］。Fujioka和Suzuki为了实现队列的横向与纵向控制，构建了包括发动机、自动变速器和轮胎在内的纵向动力学模型，并结合3自由度动力学模型设计了滑模控制器（slide mode controller，SMC）［11］。

当领航车为人为驾驶时，领航车的路径无法通过通信播报给队列中的跟随车辆，通过分布式的局部控制方法会引起横向跟踪偏差累积的问题。Solyom等［12］针对误差积累性效应，提出了侧向队列稳定性概念，设计了保证横向队列稳定性的分布式控制方法并探究了模型不确定性对稳定性的影响［12］。上述研究中，部分数据无法由被控车辆直接获取并用于分布式控制。针对该问题，McAree等提出了一种车辆队列的横向控制策略，通过车间通信设备在无法通过车载传感器获得前车位置与速度时进行控制，并在传感器和驱动存在延迟的情况下保证队列稳定性［13］。刘志强等为提高换道的安全性、稳定性和换道效率，提出了一种在智能网联条件下的多车协同换道策略，利用滚动时域优化算法对优化控制问题进行了动态求解，但该研究未探讨算法的实时性能否满足实际应用要求［14］。

根据二维场景中纵向控制器与横向控制器是否为集成式，车辆队列车辆节点的运动控制可分为独立式和耦合式。其中，独立式的运动控制器中，纵向速度控制与横向的轨迹跟踪相对独立，忽略了横纵向运动之间的耦合效应［15］，如Caruntu等提出一种利用模型预测控制（model predicted controller，MPC）进行纵向跟踪，并单独设计了比例积分控制器进行横向跟踪［16］，然而MPC计算复杂度高，需要占用较多的计算资源，依赖于高性能的计算单元［17］；耦合式的运动控制方法考虑了车辆在纵向、横向与横摆运动的耦合，并在同一控制器中同时进行控制变量的决策，实现纵向间距保持与横向的轨迹跟踪［18］。

综上所述，针对二维场景车辆队列的跟踪控制研究采用的控制方法主要为纵向与横向的单独控制，未考虑纵向间距与横向路径跟踪功能的集成控制。为解决二维场景中车辆队列跟踪控制中的纵、横向耦合问题，本文中基于参考向量场，提出通过车间通信获得领航车参考轨迹，并作为跟随车辆期望轨迹的策略，开发了二维场景下保证车辆队列实现纵向间距保持与横向跟踪功能的运动控制算法，利用哈密尔顿函数，以最小化速度矢量和横摆角速度跟踪误差为目标，构建跟踪控制目标函数进行求解，可实现横向、纵向和横摆运动的耦合最优控制；通过有约束伪逆矩阵法将车辆运动总力分配至各个车轮，解决了物理环境约束与执行器饱和下的轮胎力控制分配问题。

1 参考向量场与动力学模型

2002年，Gordon提出了一种基于速度反馈的自动驾驶车辆驾驶员模型，通过建立参考向量场（reference vector field，RVF），利用非线性反馈控制，实现了车辆的路径跟踪。该方法被广泛应用于路径规划与跟踪、障碍物避撞等方面的研究。在后续的研究中，该方法被进一步拓展应用于车辆队列的跟踪控制中［4］，其主要原理如下。

假设车辆运动被限定在二维平面中，且作为一个运动的质点进行分析。该质点具有纵向和横向两个自由度。车辆的质点动力学模型采用双积分器式，因此系统的控制量被选择为加速度，如式（1）所示。参考向量示意图如图1所示，Sd代表参考车辆与被控车辆之间的理想间距。则构建一条由被控车辆当前位置指向路径中期望点的速度向量ω。向量ω可以描述为

图1 参考向量示意图

式中：R为当前位置与期望位置的实际距离；S为路径坐标系中车辆与期望点之间的纵向跟踪误差；v为速度向量的模，在进行路径跟踪时往往设定为固定值。显然，当参考车辆沿着直线行驶时，有R=

为了保证纵向间距的可控性，需要建立参数v与纵向间距保持的紧密联系。结合误差动力学模型，令参数v为

式中：vg为参考车的速度向量；k为调整纵向跟踪误差的权重系数。

参考速度向量和实际速度向量之间的误差为

为了使得路径跟踪与间距跟踪的误差收敛，对式（3）进行微分：

其中∇ω=( ∂ωx∂x，∂ωy∂y)

当存在初始速度误差时，车辆在考虑纵向、横向、横摆方向的速度变化时，3自由度动力学模型为

式中：vx、vy和φ分别为车辆的纵向速度、横向速度和横摆角；x、y分别为车辆纵向、横向位置；Fx、Fy分别为车辆所受的纵向力与横向力；Mz为车辆的转动力矩；I为车辆转动惯量。

2 哈密尔顿参考向量场跟踪控制算法

普通的RVF跟踪算法基于质点动力学模型，无法同步决策横摆方向的运动。考虑车辆队列中车辆节点的纵向、横向与横摆方向的运动耦合效应，本文中以最小化纵向间距与横向路径跟踪控制为目标，提出一种结合哈密尔顿函数的哈密尔顿参考向量场（Hamilton⁃reference vector field，H⁃RVF）跟踪控制算法。

描述车辆横向、纵向、横摆运动的方程为非线性，因此利用泰勒展开并忽略高阶项，对其进行线性化，形成状态空间方程，如式（6）所示。

其中：

使用欧拉法对连续系统进行离散化，如式（7）所示。

其中：A t=(I+T)A

参 考 量Yref=[vxref，vyref，φref]T，则 反 馈 量Y=

构建哈密尔顿函数：

其中

最终基于H-RVF求得的输出U(t+1)为

3 有约束控制分配

在跟踪控制算法决策出车辆运动总力、总力矩后，须将运动控制器中输出的虚拟力、力矩分配到各个车轮。进行控制分配时，须考虑物理环境的约束，并进行合理假设。行驶在水平面的3自由度车辆主要物理约束包括：

（1）当车辆的后轮无法主动转向时，左右车轮转角为0，此时后轮轮胎力主要由被控车辆的质心侧偏角决定；

（2）左右车轮的转角变化率相同，在不考虑阿克曼转角的情况下，认为左轮转角等于右轮转角。

此时，该物理约束可以通过式（12）简化表示。

车辆双轨3自由度动力学模型如图2所示，每个车轮的横纵向轮胎力会形成车辆总力，二者之间满足关系：

图2 车辆双轨3自由度动力学模型示意图

其中：

矩阵N会随着车轮转角而变化，为了将其视为线性方程进行求解，本文中假设每一个计算轮胎力的采样周期内车轮转角不变。

本文中将提出一种基于加权伪逆矩阵的控制分配方法，考虑轮胎力饱和与物理约束的前提下，找到F矩阵，使NF-V误差最小：

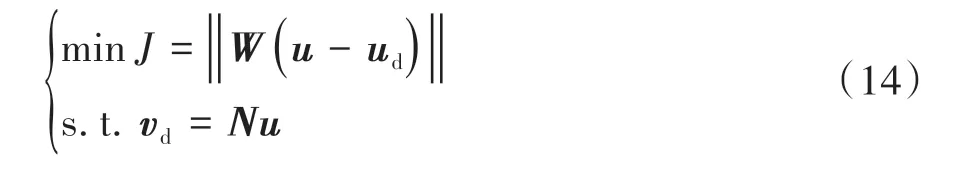
式中：vd为期望控制指令，在进行轮胎力控制分配时等于矩阵V；u为控制量；ud为期望的操纵面参考位置。

定理：对于任意虚拟指令vd，如果操纵面期望位置ud已知，且权值矩阵W对称正定，则加权伪逆分配模型的最优分配率为

式中上标#表示Moore⁃Penrose逆，即伪逆。

证明：上式为目标函数的最优解。

构造哈密尔顿函数：

式中λ为拉格朗日乘子，λ=[λ1，λ2，…，λn]。

将式（16）对u求偏导并使其等于0，则

对λ求偏导，并使其等于0，并将式（17）代入，则

最终可以得到

式中：W为正定对称矩阵；u=(I-GN)ud+Gvd；G=W-1(NW-1)#。

本方法利用该权重矩阵，可以通过调节权重矩阵获得不同满足条件的解。最终的控制量由式（19）求得。

在考虑传统前轮转向汽车物理约束时，将式（12）与式（13）结合，重新构建vd和N矩阵的拓展矩阵，如式（20）和式（21）所示。

则考虑物理等式约束的加权伪逆矩阵算法控制量可以通过式（22）获得。

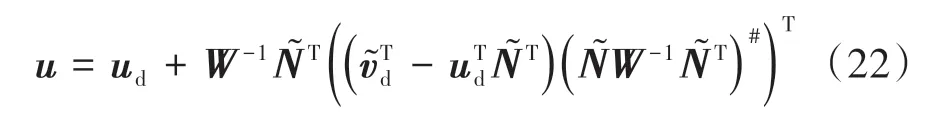
上述算法中，未考虑执行器饱和对轮胎力分配的约束。不同的附着条件对执行器饱和约束的要求不同，为使轮胎力控制分配的效果满足执行控制的需求，本文中结合摩擦圆对加权伪逆矩阵分配的轮胎力进行了进一步的修正，如图3所示，修正公式如式（23）所示。

图3 摩擦圆修正

4 仿真分析与验证

为验证本文中提出算法的有效性，采用驾驶模拟器进行仿真和实验验证。验证包括3部分：H⁃RVF纵横向耦合跟踪控制算法验证；控制分配算法验证；基于驾驶模拟器的车辆队列纵横向耦合跟踪控制算法验证。基于驾驶模拟器的队列纵横向耦合跟踪控制实验原理如图4所示。领航车的驾驶由人类驾驶员完成，分别实现纵向速度控制与横向双移线路径跟踪；跟随车由本文中提出的纵横向耦合跟踪控制算法进行控制。

图4 车辆队列驾驶仿真模拟器原理图

4.1 纵横向耦合跟踪算法对比验证

为了验证利用哈密尔顿函数对参考向量场的改善度，本文中分别构建了H⁃RVF和MPC，并将其应用于车辆队列的跟踪控制。选择了双移线（double lane change，DLC）工况，并在变化的行驶速度下进行了路径跟踪控制。其中，控制器的关键参数如表1所示［28］。

表1 控制器关键参数

图5为MPC和HRVF在纵向速度变化时的期望速度跟踪曲线。由图可知，HRVF和MPC在进行了稳定的跟踪后发生了抖动。该抖动的产生原因为横向的速度变化对纵向速度的耦合效应。通过纵横向耦合跟踪控制算法，保证了纵向速度始终通过纵向力的调整，避免对期望速度的跟踪误差偏离过大。

图5 纵向速度对比图

图6为HRVF和MPC的横向轨迹跟踪对比曲线。由图可知，MPC通过多个时域内的误差综合优化，减小了横向跟踪过程中误差跟踪波动，因此更加稳定。HRVF通过跟踪期望的速度向量，使其对误差的变化更加敏感，避免了较大的跟踪误差，然而出现了小幅度的误差波动。

图6 轨迹跟踪对比图

在对比算法的复杂度时，常使用时间复杂性来描述算法计算时间与变量数目的关系。表2为MPC与HRVF的算法实时性事后法对比（sec/sim.sec表示单位仿真时间使用的现实时间）。由表可知，HRVF的实时性远优于MPC，因此更加适用于实车的应用。

表2 耦合跟踪控制方法实时性对比

4.2 控制分配算法验证

本节内容将对比极限工况下线性二次规划控制分配法和加权伪逆矩阵分配法的控制分配性能，评价指标包括计算速度、分配误差和最大轮胎利用率等。其中，计算速度用于描述不同控制分配方法的计算实时性，分配误差用于描述控制分配方法将期望的虚拟控制信号分配的控制精度；最大轮胎力利用率描述轮胎能量耗散率和轮胎力稳定裕度。

在极限工况下，垂向载荷偏移导致的不同轮胎摩擦圆极限，并使轮胎力达到饱和。轮胎力饱和现象会使车辆进入失稳状态，造成极大的安全隐患。轮胎力饱和约束如式（24）所示。

为了对比本文中提出的控制分配算法在分配精度、实时性和轮胎力利用率等方面的具体性能，分别采集了轮胎力分布图和轮胎力利用率图。

图7和图8分别表示了不同控制分配方法各轮胎力离散点的分布情况。显然，在线性二次规划和加权伪逆矩阵等方法的控制分配下，车辆的轮胎力的分布较为集中，且分布范围最窄。

图7 线性二次规划轮胎力分配结果

图8 加权伪逆法轮胎力分配结果

图9和图10分别为两种控制分配方法下的轮胎力利用率。由于选择了较为极限的仿真工况，因此最大轮胎利用率接近并达到了100%。线性二次规划表现出较好的性能，最大轮胎力利用率均在99.57%以内。加权伪逆矩阵法轮胎力利用率未超过100%，出现该现象的原因为加权伪逆矩阵添加了摩擦圆修正部分。虽然再分配修正法最大轮胎力利用率也较大，但是由于其存在摩擦圆修正，因此可以保证其分配的轮胎力满足摩擦圆约束条件。此外，两种方法均存在抖动，该抖动主要由上层的运动控制算法导致，与车辆的运动状态相关。通过调整控制分配算法中的权重系数，抖动可以得到有效的抑制。

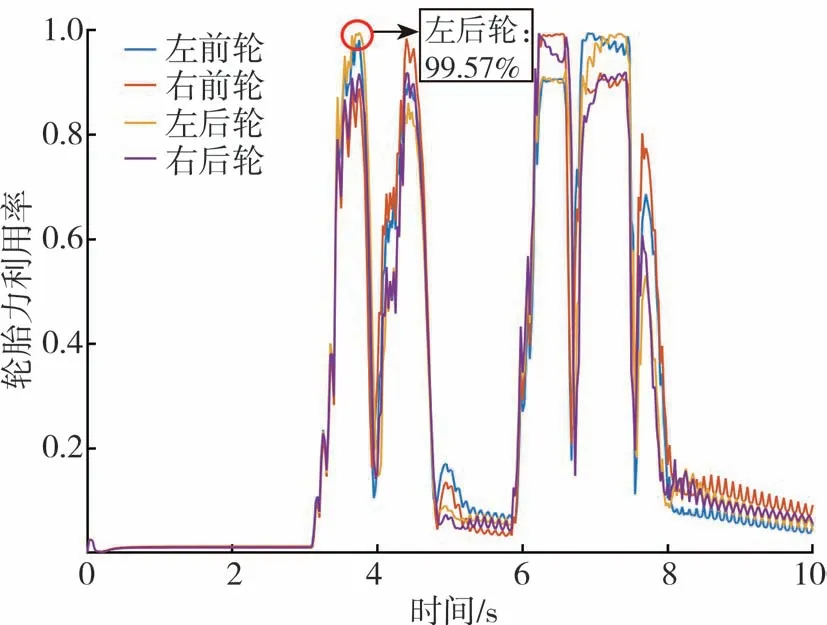
图9 线性二次规划轮胎力利用率

图10 加权伪逆法轮胎力利用率

上述两种控制分配的方法在仿真中的数据汇总和对比如表3所示。时间复杂性体现了算法在计算过程中的实时性，由表可知，基于伪逆矩阵的控制分配算法实时性优于基于线性二次规划的控制分配算法，且平均轮胎力利用率较为相似，未出现显著劣势。综上所述，基于加权伪逆矩阵的控制分配算法在满足物理约束的条件下，能够同时保证较小的轮胎力利用率和分配误差，并大大改善了控制分配算法的实时性。

表3 控制分配方法对比

4.3 车辆队列横纵向耦合跟踪控制算法验证

为了验证HRVF在车辆队列中的性能，本文中通过驾驶模拟器对其进行了队列协同控制实验。图11为双移线场景中，车辆队列横纵向跟踪过程中的纵向加速度曲线。当前车加速或减速时，加速度幅值如果逐渐放大，会导致队列下游车辆由于执行器饱和而无法实现期望的控制结果，进而导致安全性问题。图中红色箭头表明了纵向加速度幅值随车辆队列传递的变化趋势。在整个过程中，加速度幅值随着队列传递逐渐的减小，表明在当前方法的控制下，车辆队列能够满足队列稳定性。

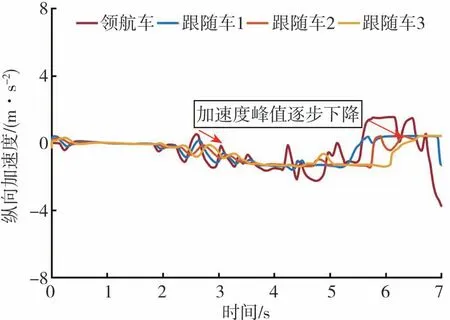
图11 车辆队列纵向加速度曲线

图12体现了行驶过程中，车辆队列纵向间距保持能力。图中，跟随车与前车的间距均在期望间距附近变化，并未随着图11中领航车加速度的变化产生较大的跟踪误差。此外，间距的跟踪误差未随着车辆队列的传递而放大。上述结果表明：本文中提出的H-RVF跟踪控制算法能够有效保证队列的稳定性的要求。

图12 车辆队列纵向间距变化

车辆队列最终行驶轨迹如图13所示。在当前速度下，跟随车未表现出明显的振荡效应与跟踪误差。表明本文中提出的纵横向耦合跟踪控制算法具有较好的横向路径跟踪控制精度。

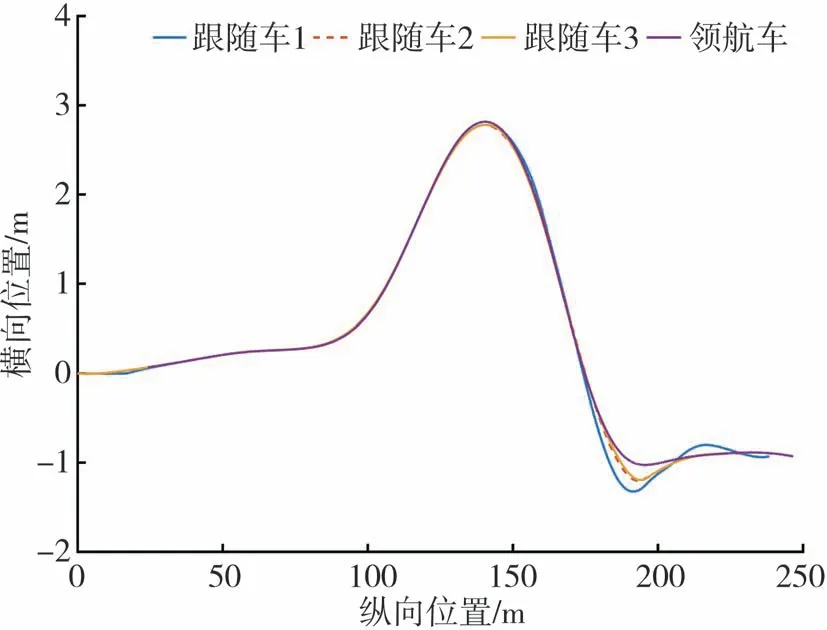
图13 车辆队列各车辆行驶轨迹图

5 结论

本文中结合基于参考向量场的纵横向耦合跟踪控制算法，针对参考向量场中质点动力学模型无法进行横摆力矩决策的问题，提出了结合哈密尔顿函数和参考向量场的HRVF车辆队列纵横向耦合跟踪控制算法。针对有约束的控制分配算法，本文中提出了基于伪逆矩阵的循环再分配算法。通过仿真分析，得出结论如下：

（1）基于伪逆矩阵的再循环控制分配法，能够在保证分配精度的前提下，大幅改善计算实时性，并满足了外界环境的约束条件；

（2）HRVF与MPC的对比表明HRVF在保证纵向与横向跟踪精度的前提下，极大地改善了计算实时性，使其更具有应用的可行性。

（3）在二维场景下车辆队列的纵横向耦合跟踪中，本文提出基于参考向量场的跟踪控制算法实现了纵向间距与横向跟踪的集成控制，避免了跟踪误差在横向与纵向的累积放大效应，保证了协同控制的安全性和稳定性。