自动驾驶汽车高速超车轨迹跟踪协调控制*
张志勇,龙 凯,杜荣华,黄彩霞
(1.长沙理工大学汽车与机械工程学院,长沙 410114;2.汽车动力与传动系统湖南省重点实验室(湖南工程学院),湘潭 411104)
前言
随着汽车保有量的迅速增加,环保、能源和交通安全问题也越来越严峻[1]。自动驾驶汽车不仅能通过优化驾驶行为部分解决环保和能源问题,也能够帮助驾驶员解放双手,克服驾驶员在复杂交通环境中的反应迟缓甚至错误操作的现象,提高汽车的行驶安全性[2-3]。汽车高速行驶过程中的超车是一种常见的驾驶行为,而自动超车不仅涉及到路径规划和速度控制,且高速行驶的安全性也不容忽视,尤其在低附着路面,车辆更容易失稳。因此必须考虑轨迹跟踪精度与横向稳定性之间的协调控制。为确保自动驾驶汽车能高效、安全地实现超车,必须解决以下3个关键问题[4-5]:合理规划超车路径和行驶速度;实现轨迹的准确跟踪;确保车辆在超车过程中的安全性和舒适性。
自动驾驶汽车轨迹跟踪的原理是利用控制算法模拟驾驶人控制车辆沿着期望路径行驶[6]。自动驾驶汽车的横向控制方法有PID控制、滑模控制(sliding mode control,SMC)等。Hwang等[7]利用带有动态前视和横摆角速度反馈的PID控制算法,将横摆运动与横向运动解耦,实现了车辆的横向轨迹跟踪控制。任殿波等[8]利用单点预瞄建立了横向位置误差模型,并利用非奇异终端滑模控制方法设计了车道保持控制策略,极大地减小了横向偏差。但上述控制方法不能约束控制输出,极有可能因控制输出饱和导致控制性能变差,甚至导致车辆失稳。而且在处理多目标时,很难实现多目标之间的协调控制。为解决上述问题,模型预测控制被应用于轨迹跟踪控制,如杭鹏等[9]设计了带控制输出约束的控制器,通过限制前轮转向角大小,改善了车辆在避障过程的操纵性能。Ji等[10]提出了多目标的模型预测控制(model predictive control,MPC)策略,提高了车辆轨迹跟踪精度和横向稳定性。但上述研究中的MPC控制器一般将多目标之间的权重设定为固定值,不能在工况变化时对多目标的控制权重进行自适应调整,很难确保控制系统具有最佳的协调性能。
涉及横向稳定性的轨迹跟踪精度协调控制需要判断当前车辆状态,并根据稳定程度确定不同目标的权重系数[11]。陈特等[12]利用横摆角速度绝对值评价车辆的横向稳定性,实现轨迹跟踪精度和横向稳定性的权重系数调整。但在质心侧偏角较大时,横摆角速度将不能准确反映车辆的横向稳定性。徐兴等[13]基于车速和路面附着系数建立了主动转向和差动转向的权重系数调整模糊规则,再根据参考轨迹的曲率修正权重系数。虽然该方法获得了较好的综合性能,但未对横向稳定性进行直接的量化评价,且模糊规则的制订需要一定的经验。车速和路面附着系数是影响车辆横向稳定性的关键因素,当横向稳定性较差时,应该增加横向稳定性的权重来保证车辆的行驶安全性;反之,则应该增加轨迹跟踪精度的权重,保证车辆的轨迹跟踪精度。因此,如何准确、定量地评价车辆的横向稳定性,是判断稳定裕度进而实现轨迹跟踪和横向稳定性协调控制的基础。
本文中针对自动驾驶汽车高速超车工况,首先规划了车辆的超车路径和期望横摆角速度;然后利用可拓集合的关联函数实现了轨迹跟踪精度和横向稳定性之间的权重系数分配,构建了自动驾驶汽车轨迹跟踪的多目标MPC可拓协调控制策略;最后通过MATLAB/Simulink和CarSim联合仿真验证了控制策略的有效性。
1 高速超车的问题描述
图1示出自动驾驶汽车在快、慢两个车道上进行高速超车的过程。开始时,车辆以纵向车速vxm行驶在慢车道中心线上,前车为Fcar,后车为自动驾驶汽车Mcar,安全车距为Hsafe。在某一时刻,车辆Mcar开始超车。超车过程分为3个阶段:第1阶段,车辆Mcar从慢车道中心线换道至快车道中心线,纵向车速提升至vxk,结束时间为T1;第2阶段,Mcar匀速向前行驶一段时间,结束时间为T2;第3阶段,车辆Mcar又换道至慢车道中心线上,车速相应降至vxm,且车辆Mcar在车辆Fcar前方Hsafe,结束时间为T3。超车过程中Fcar以车速vxm匀速向前行驶,车辆Mcar以匀加速、匀速、匀减速向前行驶。D1为第1次换道后车辆Mcar落后于车辆Fcar的距离,D2为第2次换道前车辆Mcar超前于车辆Fcar的距离。

图1 自动驾驶汽车的高速超车过程
为了保证车辆Mcar在超车过程中的安全性和舒适性,需要确保超车路径规划的合理性和轨迹跟踪的精度,其中路径规划问题可转换为如何合理规划车辆的纵向车速和横向车速。另外,由于车辆高速转向行驶,超车过程中还须确保车辆的横向稳定性和舒适性。
2 超车过程中的纵向车速规划
由于超车前Mcar、Fcar两车之间的安全车距为Hsafe,超车之后两车的安全车距仍为Hsafe,只是车辆Mcar在车辆Fcar前方。仅考虑前车突然停车时,后车与前车不发生碰撞的最小安全距离[14]为

式中:vf为后车车速;tm为系统反应时间;amax为后车最大加速度,其值与路面附着系数μ和重力加速度g有关,amax=μg;d0为安全裕量。
2.1 第1次换道过程
在换道过程中,车辆Mcar纵向速度由vxm匀加速至vxk,换道时间为T1。纵向加速度表示为

第1次换道过程中Mcar的纵向位移XM1为

Fcar一直以车速vxm匀速行驶,第1次换道过程中的纵向位移XF1表示为

要保证安全车距,须使下面的不等式成立:

则车辆Mcar落后于车辆Fcar的距离D1为

2.2 第2次换道过程
在T2时刻,车辆Mcar开始从快车道换道至慢车道,且换道时间、纵向车速变化规律与第1次换道一致。第2次换道过程中车辆Mcar的纵向加速度为

换道过程中车辆Mcar的纵向位移XM3为

车辆Fcar在换道过程中的纵向位移XF3为

同理,要保证安全车距,须使下面的不等式成立:

为了保证车辆Mcar换道之后与车辆Fcar的安全车距为Hsafe,T2时刻车辆Mcar必须超前车辆Fcar,超前距离D2为

2.3 匀速行驶阶段
在T1时刻,车辆Mcar落后车辆Fcar的距离为D1,在T2时刻,Mcar超前Fcar的距离为D2。在T1~T2的时间内,Mcar、Fcar两车匀速行驶的位移为

式中:XF2和XM2分别为车辆Fcar和Mcar匀速行驶的纵向位移。
在匀速行驶阶段,两车位移有如下关系:

由式(12)和式(13)可得匀速行驶时间为

综上所述,车辆Mcar在3个阶段的纵向车速为

3 超车过程中的横向车速规划
采用梯形横向加速度确定车辆换道过程中的横向车速,具有作用速度快,便于分析、设计和计算的优点[6,15]。梯形横向加速度变化规律如图2所示,其中aymax为横向最大加速度,K为横向加速度变化率,t1和t2分别为在慢车道上达到和结束最大横向加速度aymax的时刻,t3和t4分别为在快车道上达到和结束最大横向加速度-aymax的时刻。

图2 梯形横向加速度
文献[6]中提出的车辆换道过程中的最大横向距离Ly、最大横向加速度aymax、横向加速度变化率K,以及换道总时间T1的关系可表示为

换道时,最大横向距离Ly为一个标准车道宽度。式(16)可用于确定换道总时间、横向最大加速度和变化率。为了保证舒适性,乘员能够承受的最大横向加速度不超过5 m/s2。
如上所述,车辆Mcar在T1时刻完成第1次换道;然后在T1到T2之间匀速向前行驶;车辆Mcar在T2到T3时刻完成第2次换道。且车辆Mcar第1次换道和第2次换道的横向加速度变化规律相同,超车过程中横向加速度ay定义为如图3所示的形式。

图3 超车过程中的梯形横向加速度
对图3的横向加速度进行关于时间t的1次和2次积分,可得到车辆Mcar在超车过程中的横向速度和横向位移曲线,其中横向位移曲线表示为

4 期望横摆角速度的确定
在车辆横向稳定性控制中,一般基于线性车辆动力学模型计算期望横摆角速度,其中纵向车速和前轮转角为输入。但在车辆轨迹跟踪的主动转向控制中,前轮转角是控制器的输出,因此不能通过线性车辆动力学模型计算期望横摆角速度。为此,可利用纵向车速与道路曲率计算期望横摆角速度[16],如:

式中:vx为纵向车速;ρroad为道路曲率。
考虑到自动驾驶汽车超车换道过程中并没实际的道路,因此无法通过摄像头等外部设备直接获得道路曲率。其中一种可行的方法是利用规划的路径曲率,文献[2]中利用期望行驶路径曲率代替道路曲率来求期望横摆角速度。期望行驶路径的曲率可表示为

式中vy为车辆横向车速。
最终,车辆的期望横摆角速度可表示为

同时,车辆的横摆角速度最大值定义为

5 多目标自适应模型预测控制策略
5.1 状态预测模型
假定转向盘转角和前轮转向角只存在比例关系,没有时间上的迟滞,且直接利用前轮转向角控制车辆转向;车辆左右两侧车轮的侧偏刚度相同;忽略悬架系统、动力传动系统、轮胎横纵向力耦合和空气动力学对车辆行驶特性的影响,仅考虑横向、横摆2个自由度的车辆动力学模型如图4所示。

图4 车辆2自由度动力学模型
车辆线性2自由度动力学模型常用描述车辆转弯行驶的横向动力学,其表达式为

式中:Cf和Cr分别为前后轮胎的等效侧偏刚度;lf和lr分别为质心到车辆前后轴的距离;m为整车质量;Iz为车辆绕Z轴的转动惯量;δ为前轮转向角;φ和γ分别为车辆的横摆角和横摆角速度。
车辆横向位移是轨迹跟踪控制的关键量,其导数定义[17]为

考虑到横摆角较小,可认为sinφ=φ,cosφ=1,式(23)可简化为

取模型预测控制的状态量xd=[vyφ γey]T,控制输入u=[δ]。以横向位移ey表征车辆的轨迹跟踪精度,横摆角速度γ表征车辆的横向稳定性,取模型预测控制的性能指标为yd=[eyγ]T。由式(22)和式(24)可以得到预测模型为

其中:

由于模型预测控制中要求预测模型是离散的状态空间模型,因此取系统采样时间为Δt,将式(25)离散化为

在模型预测控制算法中,预测步长为Np,控制步长为Nc。假定在k时刻,预测步长Np内的系统预测输出向量Yc和控制输出向量ΔU为
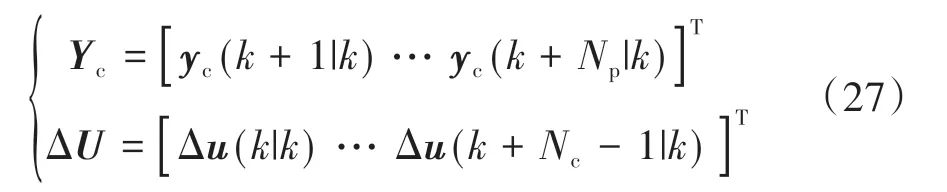
则预测步长Np内的系统状态量可表示为

综合式(27)和式(28)可得到预测步长Np内的输出表达式为

其中:

5.2 多目标函数设计
为了同时保证自动驾驶汽车超车过程中的轨迹跟踪精度、车辆横向稳定性和舒适性,需要在模型预测控制的目标函数中包含性能指标、控制增量等子目标[18]。本文定义目标二次函数为
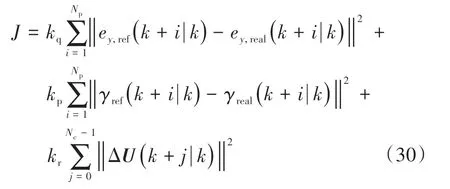
式中:ey,re(fk+i|k)和ey,rea(lk+i|k)分别为期望横向位移和实际横向位移;γre(fk+i|k)和γrea(lk+i|k)分别为期望横摆角速度和实际横摆角速度,i=1,2,…,Np;ΔU(k+j|k)为控制增量,j=0,…,Nc-1;kq、kp和kr分别为轨迹跟踪精度、横向稳定性和控制增量的权重系数。
在车辆高速行驶时,为了提高车辆轨迹跟踪精度、安全性和舒适性,将控制量及其增量和性能指标限制在一定范围内[19],如

利用二次规划求解最优前轮转向角时,在k时刻通过求解目标函数可得控制步长Nc内的解向量ΔU*(k)为

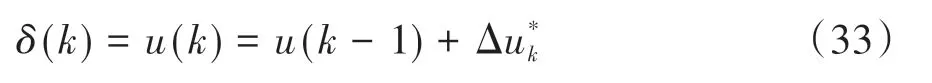
无人驾驶车辆在输入最优前轮转向角后可得k+1时刻的车辆状态,然后进入下个控制周期,重复上述过程,从而实现无人驾驶汽车的轨迹跟踪控制。
5.3 多目标可拓协调控制器设计
由式(30)可知,超车过程中需要保证两个控制性能目标,即轨迹跟踪精度与横向稳定性。为适应复杂的行驶工况,须根据车辆行驶工况,实时调整两者的权重系数,以获得最佳的综合性能。例如,在低附着路面行驶且车辆横向稳定性较差时,应增大横向稳定性的权重系数,减小轨迹跟踪精度的权重系数,优先保证车辆的安全性;当行驶在高附着路面且车辆不易横向失稳时,应增大轨迹跟踪精度的权重系数,优先保证轨迹跟踪精度。在权重系数动态调整方面,文献[12]中提出了根据横摆角速度大小的分配方法:

式中:kq和kp分别为轨迹跟踪精度和横向稳定性的权重系数;kf为kq与kp之间的调节系数。
由式(34)可知,当γreal的绝对值较大时,车辆趋于不稳定状态,增大横向稳定性的权重系数的同时减小轨迹跟踪精度的权重系数,优先保证车辆安全行驶;当γreal的绝对值较小时,车辆行驶比较稳定,增大轨迹跟踪精度的权重系数的同时减小横向稳定性的权重系数,优先保证轨迹跟踪精度。但在低附着路面,横摆角速度并不能准确反映车辆的横向稳定性。另外,在换道时车辆横摆角速度肯定会出现为零或极小的情况,根据式(34)计算的权重系数会出现极大和极小的情况,容易导致权重分配方法失效。
在考虑路面附着系数后,车辆的质心侧偏角和横摆角速度能有效描述车辆行驶的安全边界[20]。本文基于可拓学集合理论,选择车辆的质心侧偏角和横摆角速度偏差定义二维可拓集合,根据当前车辆状态在可拓集合中的投影点到稳定边界和非稳定边界的可拓距计算关联函数,实现权重系数的动态调整[21],步骤如下。
(1)特征量的提取
选取当前车辆的质心侧偏角和横摆角速度偏差为特征向量S(β,Δγ),Δγ为横摆角速度实际值与期望值的偏差;并在如图5所示的二维可拓集合中找到与之对应的Pm点。

图5 二维可拓集合
(2)可拓集合划分
横向稳定性不同区域的边界如下:横摆角速度偏差的经典域与可拓域的边界值Δγ1为|s1Δγ|,可拓域与非域之间的边界值Δγ2为|s2Δγ|,s1、s2为大于0小于1的常数;质心侧偏角的经典域与可拓域的边界值β1通过横摆角速度增益的线性区和非线性区的界限确定,可拓域与非域的边界值β2取arctan(0.02μg)。
(3)关联函数计算
将Pm与原点连接并延长,与可拓域外边界相交于P1和P4,与经典域边界相交于P2和P3。
Pm点与较近的经典域边界点和可拓域外边界点相对距离分别表示为dkt和djd,在外边界点之外为正,否则为负。具体计算方法如表1所示。

表1 可拓距计算方法
而关联函数K(S)则用来确定点Pm所处的区域:经典域、可拓域还是非域,其计算公式为

(4)多目标权重分配
当K(S)≥1时,此时Pm处在经典域中,车辆横向稳定性较好,可仅关注轨迹跟踪精度,因此kq=1,kp=0。
当0≤K(S)<1时,此时Pm在可拓域中,车辆的横向稳定性较差,但未达到失稳的程度。Pm越接近非域,则关联度函数K(S)的值越小,符合轨迹跟踪精度权重的变化要求,因此kq=K(S),kp=1-K(S)。
当K(S)<0时,此时Pm处在非域中,车辆处于横向失稳状态,应以改善车辆横向稳定性为重点,暂时忽略轨迹跟踪精度,因此kq=0,kp=1。
通过上述4个步骤,由车辆的横向稳定性裕度实现轨迹跟踪精度与横向稳定性的权重分配,达到两个目标的协调控制。
6 控制性能分析
为了验证本文所提出的超车轨迹跟踪多目标MPC可拓协调控制策略算法的有效性,基于MATLAB/Simulink和CarSim建立了控制系统的联合仿真平台,如图6所示。

图6 控制系统的联合仿真示意图
在大地坐标系下,车道宽为3.75 m,车辆初始位置为(0,1.875 m);y=1.875 m为慢车道中心线,y=5.625 m为快车道中心线。车辆动力学模型的主要参数如表2所示。采用文献[6]中所列的工况对控制系统进行仿真验证。慢车道车速为72 km/h,快车道车速为108 km/h。换道时间为6 s时,梯形横向加速度中最大横向加速度为0.5 m/s2。

表2 车辆动力学模型参数
由图6所示的控制系统联合仿真示意图可知,首先将超车路径规划器中计算出来的期望超车路径和期望横摆角速度作为轨迹跟踪模型预测控制器的参考值,结合上一时刻CarSim车辆动力学模型输出的车辆实际横向位移和实际横摆角速度,通过在轨迹跟踪模型预测控制器中进行滚动优化求解出当前时刻的最优前轮转向角,并作用于CarSim车辆动力学模型。其中,在计算期望横摆角速度时,先由式(19)根据期望超车路径计算超车路径的曲率,再由式(20)计算超车过程中的期望横摆角速度。
6.1 MPC与SMC控制性能对比
为对比MPC与SMC[22]的控制效果,进行不同路面附着系数下的数字仿真。由于SMC为单目标控制,故只能与单目标MPC对比,因此将式(30)中的kp设为零,即在仅考虑轨迹跟踪精度的单目标条件下,对比MPC与SMC的控制性能。路面附着系数分别设置为μ=0.85和μ=0.3。图7为MPC与SMC在两种路面附着下的高速超车轨迹跟踪精度分析。由图可知,在μ=0.85时,单目标MPC与SMC都能控制自动驾驶汽车准确跟踪超车过程中的期望轨迹,SMC控制下的横向位置误差最大值和均方根值分别为1.35和0.59 m,单目标MPC控制下的横向位置误差最大值和均方根值分别为0.3和0.12 m,后者的两种误差分别比前者减小了77.78%和79.66%。当μ=0.3时,由图7(a)可知:SMC控制下的车辆已经完全偏移了期望轨迹,无法实现轨迹跟踪控制;但MPC控制的车辆仍能精确地控制车辆沿期望轨迹行驶,且高、低附着路面下的轨迹跟踪精度非常接近,说明MPC控制方法的鲁棒性明显高于SMC。

图7 轨迹跟踪精度分析
图8为两种路面条件下MPC与SMC的车辆横摆角速度及其误差的对比。由图8(a)可知:当μ=0.85时,SMC和MPC都具有较好的横向稳定性;当μ=0.3时,SMC横向稳定性显著变差;虽然MPC的横向稳定性优于SMC,但也已明显偏离期望值。由此可知,在低附着路面条件下,仅考虑轨迹跟踪精度的轨迹跟踪控制,不能保证车辆的横向稳定性,容易导致车辆横向失稳,因此有必要协调轨迹跟踪精度与横向稳定性,也即采用多目标MPC控制。

图8 横向稳定性对比分析
6.2 多目标可拓MPC协调能力分析
如第5.3节所述,多目标MPC控制须进行多目标间权重的分配,并鉴于采用文献[12]中所提出的单横摆角速度评价(single yaw rate evaluation,SYRE)方法进行权重分配的不足,基于可拓集合理论,提出了权重系数动态调整的方法,即所谓可拓MPC。下面通过3个对比,进行可拓MPC协调性能的分析,工况的设置为:换道时间T1=6 s,路面附着系数μ=0.3。
(1)图9为两种权重分配方法下超车过程中的轨迹跟踪精度的对比。由图可知:采用SYRE进行控制权重分配时的轨迹跟踪误差较大,横向位置误差的最大值和均方根值分别为0.53和0.18 m;采用可拓MPC分配权重时,对应的误差为0.41和0.11 m;后者比前者分别减少了22.64%和38.89%,说明本文提出的权重分配方法能有效提高车辆的轨迹跟踪精度。

图9 可拓MPC与SYRE轨迹跟踪精度对比
图10为两种权重分配方法的横摆角速度及其误差的对比。由图可知:采用SYRE进行控制权重分配时,车辆横摆角速度误差最大值为3.20°/s,均方根值为1.28°/s,在完成第1次换道后进入匀速行驶时,相对于期望值出现了很大的偏差,且从10 s开始出现比较明显的振荡;采用可拓MPC控制分配权重时,横摆角速度误差的最大值为2.48°/s,均方根值为0.95°/s,后者的两种误差值分别比前者减小了22.52%和25.78%,说明提出的可拓集合权重分配方法能有效地改善车辆的横向稳定性。

图10 可拓MPC与SYRE横向稳定性对比
(2)为更便捷而清晰地对比不同控制策略的性能,将图7~图10的误差数据汇总于表3,其中,ey⁃max和ey⁃rms分别为横向位置误差的最大值和均方根值;eγ⁃max和eγ⁃rms分别为横摆角速度误差的最大值和均方根值。

表3 不同控制策略的轨迹跟踪精度和横向稳定性指标对比
由表3可见:可拓MPC的横向位置误差最大值(0.41 m)比单目标MPC的(0.31 m)增大了32.26%,但其均方根值减小了8.33%;可拓MPC横摆角速度误差的最大值(2.48°/s)比单目标MPC的(4.06°/s)减小了38.92%,且更接近期望值;对应的均方根误差减小了51.03%,说明可拓MPC在协调轨迹跟踪精度与横向稳定性时,通过降低轨迹跟踪精度来提高车辆的行驶安全性,使车辆在低附着路面也具有较好的横向稳定性。
(3)图11为两种权重分配方法的前轮转向角和横向加速度对比。由图可见:控制权重采用SYRE进行分配时,最大前轮转向角为12.20°,采用可拓集合进行控制权重分配时,最大前轮转向角为9.90°,后者比前者减小了18.85%;在反映乘坐舒适性的横向加速度上,SYRE分配方法的横向加速度最大值为1.10 m/s2,均方根为0.48 m/s2。可拓集合分配方法的横向加速度最大值为0.82 m/s2,均方根为0.32 m/s2。后者比前者分别减小了25.45%和33.33%。由此可见,本文提出的可拓集合权重分配方法还能有效地改善车辆在超车过程中的乘坐舒适性。

图11 可拓MPC与SYRE乘坐舒适性对比
从表3并结合(3)的对比,可以看出:在4种不同控制策略中,单目标下,MPC的超车轨迹跟踪精度优于SMC;而多目标下,可拓MPC的轨迹跟踪精度、横向稳定性以至乘坐舒适性皆优于SYRE。
7 结论
针对自动驾驶汽车高速超车过程中的轨迹跟踪协调控制,以横向位置偏差、横摆角速度跟踪偏差和控制增量为优化目标,建立了超车轨迹跟踪多目标MPC可拓协调控制策略。单目标下的超车轨迹跟踪精度分析结果表明:在高、低路面附着系数下MPC都能保证车辆的轨迹跟踪精度,且具有较好的鲁棒性;多目标下,基于可拓集合理论提出的轨迹跟踪和横向稳定性权重系数动态分配方法,在低附着路面条件下,不仅能有效保证车辆的轨迹跟踪精度,而且能改善车辆的横向稳定性和乘坐舒适性,具有较好的综合性能。

